基于元件冗余的有源电力滤波器容错控制方法研究
胡常胜,李杨,单强,刘辉
(国网新疆电力有限公司,新疆 乌鲁木齐 830000)
随着控制理论以及计算机技术的飞速发展,各种电力电子设备被广泛应用于人类的日常生活以及工业生产过程中[1-2],虽然这些电子设备能够给人类带来一定的效益,但是应用到电力系统中时也带来了一些比较严重的谐波问题。如何设计一个良好的容错控制策略对有源电力滤波器(APF)进行有效控制成为当前研究的核心问题。
相关专家给出了一些较好的研究成果,例如李颖等人[3]在电力电子器件发生故障时,通过剩余的设备组建三相四开关逆变器替换故障的三相四开关逆变器,在消除故障的同时还能够有效进行APF控制。张建忠等人[4]重点分析T型三电平逆变器功率开放故障后的运行状态,利用空间矢量脉宽调制和逆变器输出完成故障诊断,进而结合APF的运行特点,提出一种控制策略,最终实现容错控制。
上述两种方法虽然取得了较为理想的研究成果,但是由于未能在控制器和控制策略设计过程中引入李雅普诺夫稳定性定理,造成容错控制误差上升,执行效率及容错率降低。为此,提出一种基于元件冗余的有源电力滤波器容错控制方法。仿真实验结果表明,所提方法不仅可以大幅度提升执行效率和容错率,同时还能够降低容错控制误差。
1 有源电力滤波器容错控制
1.1 三相四开关拓扑结构分析和去冗余数学模型的建立
随着APF研究的不断深入,已有大量的设备投入到实际应用中,并联型是APF中十分常见的一种。现有的APF主要使用三相六开关拓扑,所以对应的有关APF理论的研究全部是针对三相六开关的拓扑结构。在上述工作原理的基础上,提出了一种基于开关冗余的三相四开关容错拓扑结构,如图1所示。

图1 三相四开关APF拓扑图Fig.1 Topology of three-phase four-switch APF circuit
图1中,三相四开关APF的b相、c相桥臂各由两个IGBT和续流二极管组成,a相直接连接到直流母线中点。假设两个串联的电容器完全相同且电压相等(即C1=C2=C,uC1=uC2),且esa+esb+esc=0,ica=icb=icc=0,abc坐标系下的三相四开关APF的状态方程为

电压型的APF在工作过程中需要有效控制直流侧电容电压,使其维持在固定的范围内,设定C1和C2两者的均值为C,综合分析相关内容能够将直流侧的电容电流[5-6]表示为
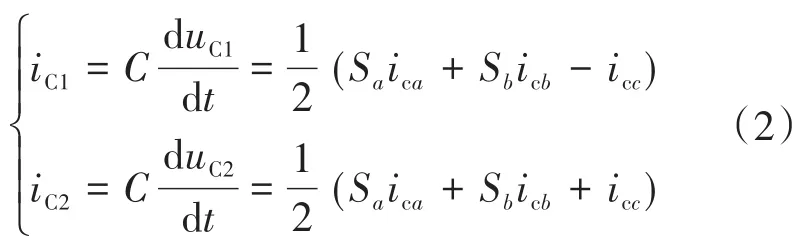
由于Udc=uC1+uC2,将式(2)中的两项相加,则能够得到以下的计算式:
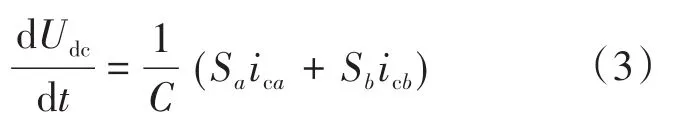
式中:Udc为直流侧总电压。
根据控制开关进行通断,促使逆变器最终输出PWM电压波。由于电压的APF损耗较小,且投资方便,效率高,对系统产生的影响较小,是当前APF主要选取的拓扑结构[7-8]。其中三相六开关APF主要是以三相PWM逆变器作为拓扑结构,通过逆变器输出的电流情况,有效判定逆变器的输出电压。另外,直流侧电压保持恒定,将其设定为逆变器的直流侧电源。当采用SPWM进行控制时,三相输出桥臂开关管控制信号主要是通过三角载波和调制波对比获取,各个桥臂上、下管开关触发信号进行互补,将各个桥臂采用统一的三角载波进行对比。选取合适的指令电流计算方法以及电流控制方法,促使APF输出和谐波大小一致方向相反的电流,主要目的是进行谐波补偿。
当熔丝串联到逆变器的输出端时,能够有效完成故障桥臂隔离。当检测出任意桥臂为故障桥臂后,需要禁止桥臂内的驱动信号运行,触发对应的双向晶闸管导通。设定A相为故障桥臂,发出的故障信号通过TRa进行导通,促使快速熔丝Fa、双向晶闸管TRa以及直流母线电流和功率器件形成回路,Fa被存储于母线电容中的能量熔断,同时将A相桥臂隔离。当故障桥臂被隔离之后,该桥臂不会对系统的运行产生任何负面的影响。此时,开关冗余逆变器拓扑结构根据故障切除和重构,A相桥臂被直流母线串联电容取代,将直流母线串联电容的重点设定为A相的输出继续进行工作,此时逆变器处于三相四开关的运行状态。其中元件冗余逆变器不需要电机绕组的中性点[9],整体电路结构简单,设备利用率较高,被广泛应用于三相逆变器场合,同时能够将其作为三相六开关APF的容错结构。
数学模型是进行理论分析的基础,为控制策略的选取以及设计提供对应的理论基础,同时还能够为仿真以及实验研究提供一定的理论支持。另外,在元件冗余的状态下,将三相六开关APF重新构建为三相四开关APF,同时将三相四开关并联型中的电压电流作为参考,在模型建立的过程需要进行以下的假设:
1)无需考虑功率器件的导通压降以及开关损耗;
2)当系统三相交流电压为理想状态时,其中各项电压只包含基波正序电压;
3)不考虑电网线路的阻抗;
4)直流侧电容、各相分别输出不同的电感以及内阻均相等。
以下对三相四开关APF拓扑进行数学建模,具体的操作过程如下:
为了简化分析过程,设定各个桥臂半导体开关器件对应的开关函数为

设定直流侧电容中点即为中性点,同时设定直流两侧电容电压为Udc/2,uAN,uBN,uCN分别表示各相电压,则能够得到以下的计算式:
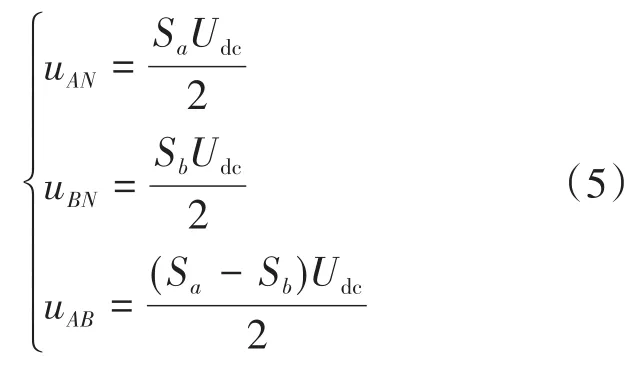
通过基尔霍夫电压定理可以得到:
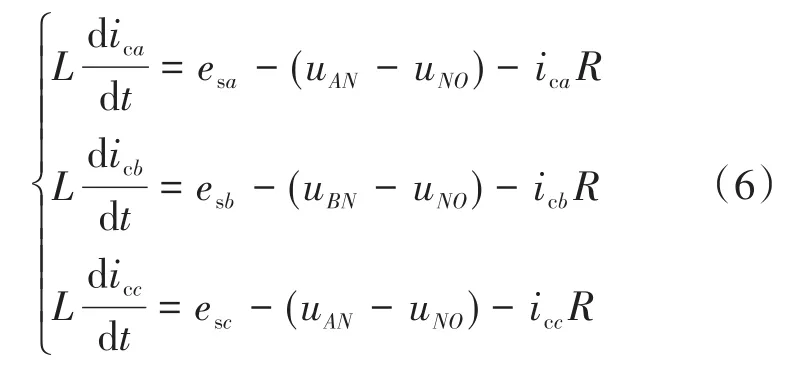
式中:esa,esb,esc为公共连接点处的电压;ica,icb,icc为APF的输入电流;uNO为基波正序电压。
将式(6)中的三相进行相加[10],由于在三相四开关的状态下输出电压电流之和取值均为0,则有:

将式(5)和式(7)联立,得到APF的三相输出电压计算式:

设定直流侧电容电压分别为uC1和uC2,当满足如下的约束条件Udc=uC1+uC2,则能够将式(8)改写为[11]

在dq坐标系下进行建模是将abc三相静止坐标系转换为dq旋转坐标系[12]。针对旋转坐标系参考方向进行适当选择,将d轴和电网的电动势两者重合[13],其中d轴表示基波有功分量的参考方向,q轴表示基波无功分量的参考方向,这样能够有效促进不同分量的独立控制。将式(9)通过矩阵的形式表示:
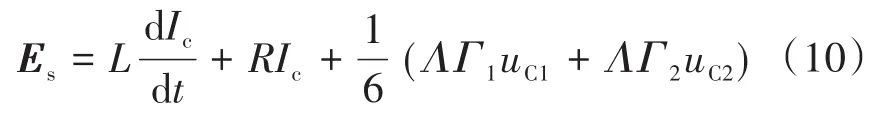
式中:L为APF输出电感;R为电阻;Ic为APF的输出电流;Γ1,Γ2为开关频率。
综合分析,能够获取dq坐标系下的去冗余数学模型,即
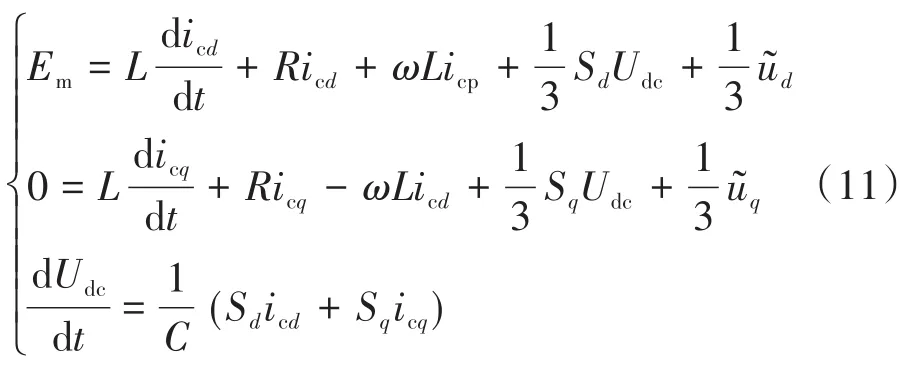
式中:icd,icp,icq为 APF的输出电流;Sd,Sq分别为直流和交流开关函数。
1.2 基于元件冗余的有源电力滤波器容错控制
当精准分析有源电力滤波器内部的拓扑结构后,在dq坐标系中组建相应的系统数学模型,经过dq坐标变换后可以将谐波电流和直流侧电压分别进行控制,最后引入李雅普诺夫稳定性原理提出一种新的电流环节控制策略,确保整个取值固定在设定的期望值上,最终完成控制。为了更好地说明控制器的设计流程,需要通过李雅普诺夫稳定性原理进行控制器设计[14],并且需要满足以下的约束条件:
1)V(0)=0;
2)针对随机x≠0,则V(0)>0;
3)当||x||逐渐趋于无穷时,V(x)也逐渐趋于无穷。
根据李雅普诺夫稳定性原理设计控制规则,当系统经过控制后APF的4个开关需要经过多次开关切换以后才能够达到平衡点0,并且保持在对应的邻域内。设定李雅普诺夫函数,具体的表达式如下:

式中:X为区域基本矢量运行时间;T为转置符号。通过李雅普诺夫稳定性定理可知,当X≠0时,需要设计一种控制策略使X≠0成立。通过坐标变换将abc三相静止坐标系下的状态方程变换到dq旋转坐标系中,则能够得到以下的计算式:
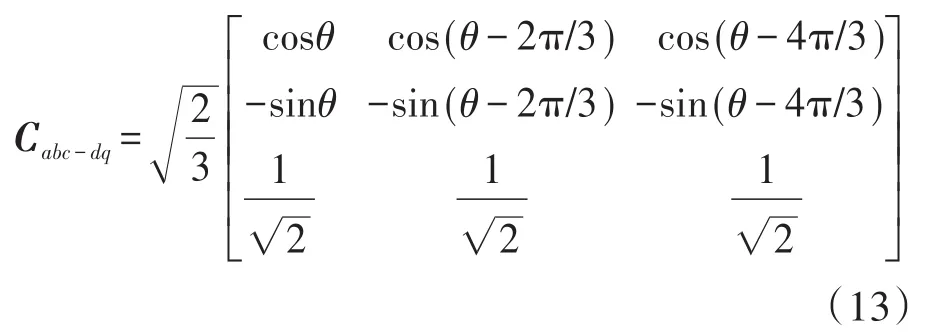
式中:ω为基波电压的角频率。
滤波器在dq坐标系下的状态方程可以表示为

在元件冗余的情况下,对有源电力滤波器进行容错控制的主要目的是为了使补偿电流能够更加精准地跟踪谐波指令电流,促使直流侧电容电压达到期望值状态[15]。由于直流侧电压波动速度明显低于谐波电流,所以整个系统可以划分为电流内环和电流外环分别进行控制。在设计控制器的过程中需要设定直流侧的取值,在dq坐标系中有源电力滤波器对应的电流环数学模型方程为

设定电流误差为

李雅普诺夫对应的方程表示为
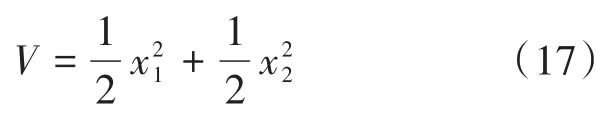
李雅普诺夫方程对应的导数为
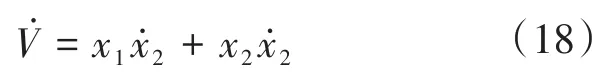
为了使导数为负数,需要促使以下的关系式成立,即
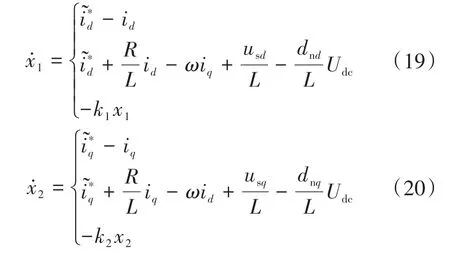
式中:k1,k2分别为谐波电流和直流侧电压比例系数。
其中所设计的控制器为

在上述分析的基础上,还需要使用比例积分控制将电压保持在期望值范围内,最终有效实现有源电力滤波器容错控制。
2 仿真实验
为了验证所提基于元件冗余的有源电力滤波器容错控制方法的综合有效性,通过Matlab/Simulink的电力系统进行仿真实验分析,为了验证本文所提出的控制算法,设计了一个容量为1 kV·A的低压三相四开关APF实物实验平台,如图2所示。实验过程中所使用的主要参数为:电压400 V,频率60 Hz,直流侧电压1 200 V,输出电抗0.03 Ω,系统阻抗8 Ω。

图2 APF实验平台Fig.2 APF experimental platform
1)有源电力滤波器容错控制误差。为了验证各个方法控制结果的好坏,实验选取有源电力滤波器容错控制误差作为测试指标,其中误差越高说明容错控制效果越差;反之,则说明容错控制结果越理想。表1给出三种不同方法的有源电力滤波器容错控制误差。由表1中的实验数据可知,随着实验次数的持续增加,文献[3]方法和文献[4]方法的有源电力滤波器容错控制误差均处于直线上升趋势,而所提方法结合李雅普诺夫稳定性定理设计的全新的控制器以及控制策略,能够有效地减少容错控制误差,获取较为满意的控制结果。
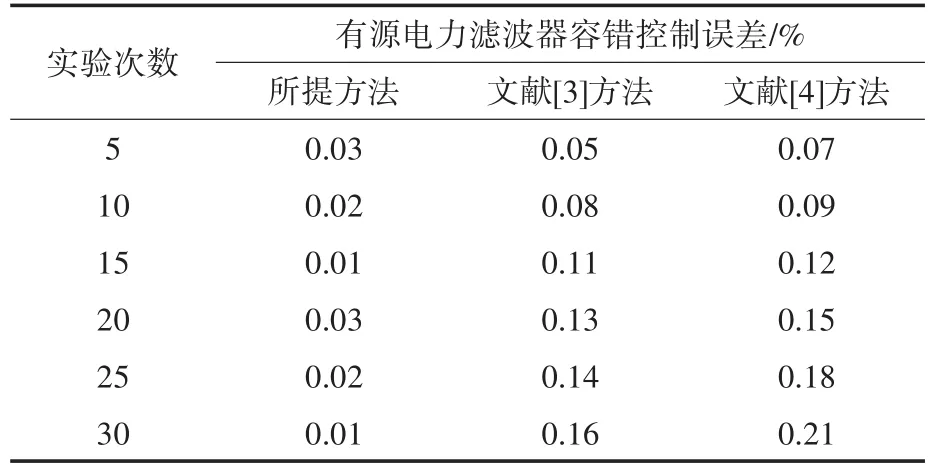
表1 不同方法的有源电力滤波器容错控制误差对比结果Tab.1 Comparison results of fault tolerant control errors of active power filter with different methods
2)执行效率。由于不同方法的操作流程完全不同,所以各个方法的执行效率也存在十分明显的差异,图3给出详细的实验对比结果。
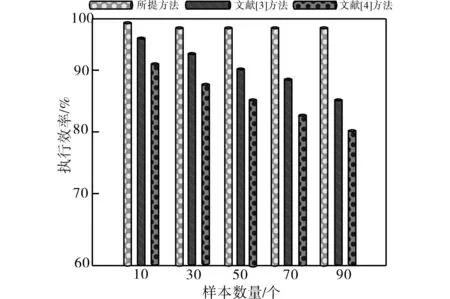
图3 不同方法的执行效率对比结果Fig.3 Comparison results of execution efficiency of different methods
分析图3中的实验数据可知,相比另外两种方法,所提方法能够以更快的速度完成有源电力滤波器容错控制,这主要是因为所提方法在控制策略以及控制器设计的过程中引入了李雅普诺夫稳定性定理,促使整体的控制性能得到提升。
3)容错率。当各个方法具有较高的容错率时,则说明其能够获取更加理想的控制效率,三种不同方法的容错率对比结果如图4所示。
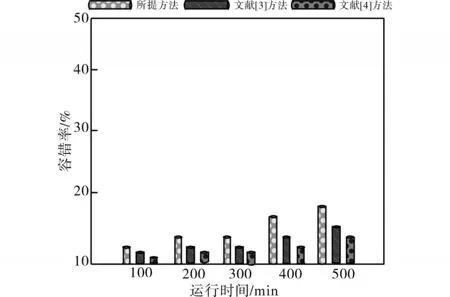
图4 不同方法的容错率对比结果Fig.4 Comparison results of fault tolerance rate of different methods
分析图4中的实验数据可知,所提方法具有较高的容错率,能够全面提升控制结果的准确性,同时也充分验证了所提方法的优越性。
3 结论
针对传统方法存在的弊端,提出一种基于元件冗余的有源电力滤波器容错控制方法。仿真实验结果表明,所提方法不仅能够有效提升容错率和执行效率,同时还能够有效减少有源电力滤波器容错控制误差,获得较为满意的控制效果。人们将有源电力滤波器广泛地应用于各种电力系统中,如配有变频设备等类似负载的场合、配有不稳定负载的场合、钢铁厂、有色金属冶炼、港口机械等。APF采用DSP+FPGA全数字控制方式,具有极快的响应时间,先进的主电路拓扑和控制算法,精度更高,运行更稳定;模块化设计,体积小,安装便利,方便扩容;一机多能,既可补谐波,又可兼补无功。由于个人精力以及时间有限,导致整个方法在研究过程中仍然存在一定的不足,后续仍将对其进行进一步完善。

