光伏驱动新能源同步机并网的调频能力研究

付文启，黄永章，2，杨鑫，管飞，谷昱君

（1.华北电力大学新能源电力系统国家重点实验室，北京 102206；2.华电（烟台）功率半导体技术研究院有限公司，山东 烟台 264000）

当前，并网新能源机组不含转动惯量或转动惯量被隐藏起来[1-2]，随着电力系统逐渐转型升级为光伏、风电等新能源主导的电网形态，具备惯性响应能力和调频能力的火电机组的占比将逐渐减小，这势必会削弱电网的频率稳定能力。因此，合理安排光伏、风电等新能源机组补充一部分惯量，承担电力系统一次调频任务是未来电力行业发展的必然趋势[3-4]。

为使新能源机组具备惯性响应能力和一次调频能力，国内外众多学者聚焦于对新能源并网换流器控制策略的改造。对于风电机组，文献[5-6]采用虚拟惯量控制，建立起风机转子转速与电网频率间的耦合关系，使得风机能够释放部分转子惯量以响应电网频率变化，并配合下垂控制参与系统一次调频。而光伏机组不同，由于不含旋转元件，无法通过控制调动与电网解耦而隐藏的“惯量”，只能利用减载运行或配备储能方式下的有功备用提供虚拟惯量[7]，目前对该方面研究多为光伏虚拟同步发电机（photovoltaic virtual synchronous generator，PV-VSG）控制[8-10]，通过将发电机转子运动方程嵌入换流器控制中来模拟惯量，其能量来源与实现方式与新能源机组的虚拟惯量控制无异。为增强新能源电网的一次调频能力，新能源机组通常通过在换流器控制环节中引入下垂控制模拟常规机组参与一次调频[11-12]，其本质是建立新能源输出功率与电网频率之间的耦合关系，当电网频率变化时，新能源机组能根据反馈信号作出功率响应，与常规机组调速器较慢的开关汽门的机械动作速度不同的是，凭借电力电子换流器的快速响应能力，新能源机组能更加迅速地调动有功储备参与系统调频[13-14]。目前已有在大电网中的试验证明，在相同故障水平和惯量水平下，并网光伏机组的快频响应作用能提供比常规机组调速器作用更强的一次调频能力[15]。若光伏机组具备无延时惯性响应能力来搭配下垂控制，光伏机组将为电网提供优于常规机组的频率支持能力。以上改进都是着眼于换流器控制策略上，下垂控制得益于换流器的快速响应，能提供优越的一次调频能力，然而，由于模拟惯性响应的控制存在检测时延或为防止过高能量冲击而在其中加入一阶惯性环节等原因，导致控制仍然无法如同步机组一般做到无响应延迟[16-17]，因而未能真正满足系统需求。

为此，文献[18]提出了新能源驱动新能源同步机（motor-generator pair，MGP）并网的新方法，利用同步电机的优良属性，可以为电网提供无延时的、真实的转动惯量；文献[19]提出了MGP的源-网相位差控制策略，并通过仿真和实验验证了在该控制策略下MGP可以稳定地向电网传输功率；文献[20-21]证明MGP能提供比同容量火电机组更多的阻尼，增强新能源电网的功角稳定性和频率稳定性；文献[22-23]通过实验验证MGP能够为光伏系统提供惯性支持，并得出其惯性响应能力比同质量块且同容量的火电机组更强的结论。

但上述文献只着眼于MGP本身的性能属性，并未进一步研究MGP惯性响应与光伏系统有功功率响应配合参与电力系统一次调频之间的控制方法。本文从MGP的系统结构和控制策略出发，揭示了MGP与虚拟惯量控制在惯量释放机制上存在本质区别，得出MGP能提供更强惯性响应能力的结论，然后在光伏经MGP并网的控制策略基础上引入下垂控制，使得MGP能调动光伏系统的有功储备参与电力系统一次调频，最后通过PSCAD 3机9节点仿真系统和5 kW实验平台对研究结果进行了验证。

1 MGP系统与控制策略

1.1 MGP并网系统结构

MGP系统结构如图1所示，MGP系统主体由一个联动轴串联两台同容量的同步电机组成，其中一台作为同步电动机（synchronous motor，SM），另一台作为同步发电机（synchronous generator，SG），忽略轴两端两个旋转刚体间振荡的影响，则两台电机始终保持运行在同转速、同转向的状态。MGP的SM与SG内部各有一个功角δM和δG，若忽略两个转子间初始相角差，则MGP系统外特性上表现出来的两端电压相角差为

图1 MGP系统并网结构图Fig.1 The grid connection system structure of MGP

根据图1可知，新能源驱动MGP并网的有功功率传输方式以转矩形式表现为：新能源发出的有功会给SM施加一个电磁转矩TeM，该电磁转矩TeM会带动SM旋转并输出一个机械转矩TmM，由于MGP系统的SG与SM同轴转动，因而SG将获得一个机械转矩TmG，然后向电网输出一个电磁转矩TeG，SG的机械转矩TmG与SM的机械转矩TmM关系为

式中：ΔTm为两台电机之间功率传输的机械转矩损耗。

1.2 直流电压反馈策略

从MGP的功角特性[19]可知，MGP输出功率与MGP两端电压相角差δMGP成正比，当MGP并网运行时，MGP发电机侧的电压相角跟随参考电网电压固定，因此通过控制电动机侧电压相角变化就能控制MGP的输出功率。

只要根据MGP的功角特性与光伏板的运行特性，建立MGP电动机侧电压相角与光伏板直流母线电压间的关系式作为换流器的控制信号，就能通过控制光伏板直流母线电压以实现控制MGP传输功率的目的，由此可得图2所示的MGP的电压反馈控制的控制框图。控制原理为：当光伏板直流母线参考电压Uref与实际电压Udc存在偏差时，该偏差值经过PI调节和脉宽调制转换为相位偏差信号，控制MGP输出功率变化，直流母线电压也随之改变，最后稳定在参考值上。

图2 MGP直流电压反馈控制Fig.2 DC voltage feedback control of MGP

直流电压反馈控制实现了MGP对光伏系统传输有功功率的跟踪，但并未建立光伏系统有功传输与负荷端有功需求间的耦合关系，当源-网功率不平衡造成系统频率突变时，光伏系统依然无法对此做出功率响应。

2 MGP惯性与改进控制策略

2.1 MGP的惯性响应原理

2.1.1 MGP的电气-机械模型

MGP同轴旋转的两台同步电机转子能够提供无延时的、真实的转动惯量。根据同步电机理论可得MGP惯性时间常数表达式为

式中：MSM，MSG分别为电动机和发电机惯性时间常数；mSM，mSG分别为电动机和发电机质量；RSM，RSG分别为电动机和发电机截面半径；ω0为MGP额定转速；SB为MGP额定容量。

假设同步电机转子截面半径都相同，与火电机组相比，尽管MGP额外多了一个转子质量块，但不具备原动机部分低压缸和高压缸两个质量块的质量，因此通过计算可得MGP的惯性时间常数约为同容量火电机组的0.66倍[19]。

根据同步电机理论，以MGP发电机端电压相角为参考值，SG的转矩方程为

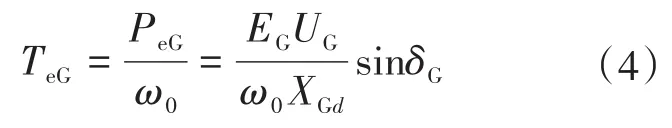
式中：EG，UG分别为SG的内电势和端电压；XGd为SG的定子d轴电抗。

将式（4）标幺化，并给SG的功角δG施加一个小扰动ΔδG，则SG的电磁转矩变化量表达式为

将式（5）线性化后表示为

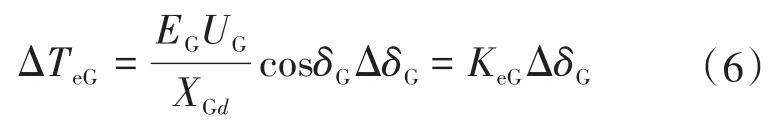
式中：KeG为SG的电磁转矩系数。

忽略MGP联动轴两端刚体间的振荡影响，可得：

同步电机转子转速与功角之间的关系为

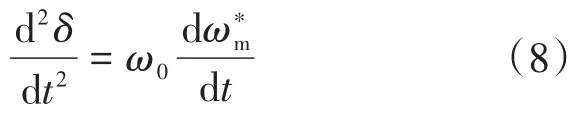
MGP转子运动方程为[14]

式中：KDM，KDG分别为SM和SG的阻尼系数；Δω*m为转子转速变化的标幺值。

将式（6）～式（8）代入式（9）的MGP的转子运动方程，并以变化量形式表达：

对式（10）、式（11）进行拉普拉斯变换后可得：

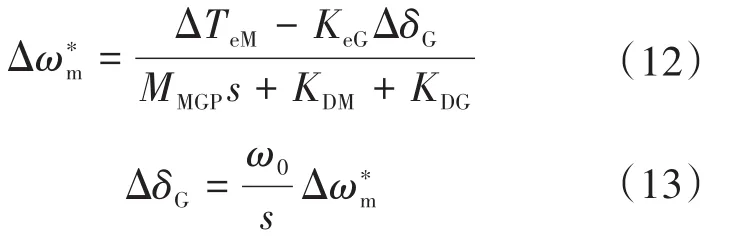
由式（12）、式（13）可得如图3所示的MGP的电气-机械模型。

图3 MGP的电气-机械模型Fig.3 Electrical-mechanical model of MGP

2.1.2 与虚拟惯量控制的惯性响应能力对比

由MGP的电气-机械模型可知，MGP的惯性和阻尼表征为状态量的形式，是其固有属性。光伏经MGP接入电网后呈现电压源特性，一旦电网频率变化引起SG电压相角改变，由于同步电机的转子运动特性和电磁暂态特性，MGP将无延时发出阻尼和惯性响应，对于时刻处在波动状态的电网频率，MGP不需要通过控制手段就能自然地响应频率变化。光伏经换流器直接并网，通过虚拟惯量控制调整光伏有功输出来模拟同步电机的惯性响应，虚拟惯量实际表征为输出量的形式，响应形式的本质不同，并且控制也存在延时，并未满足系统真正需求，而且，在电网频率时常变动情况下，控制的频繁动作也存在可靠性问题。

光伏经MGP并网，仅凭MGP的惯性响应就能平抑电网频率小波动，然而，一旦电力系统触发大干扰事件，MGP短时的惯量支撑作用还不足以胜任调频任务。根据图3的电气-机械模型可知，通过改进MGP的直流电压反馈控制，加入一个反馈控制环节，建立起SM的电磁转矩TeM与SG功角δG或转速ωm之间的联系，就能调用光伏系统有功储备参与系统一次调频。

2.2 基于PV下垂控制的直流电压反馈控制策略

参考常规发电机组的静态功频特性，当电网频率发生变化后，发电机组将改变有功功率出力保证电网频率偏差在允许范围之内，根据发电机组有功出力与电网频率偏差之间的关系，可得光伏系统驱动MGP的下垂控制系数的表达式：

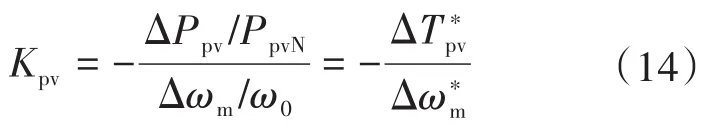
式中：ΔPpv，PpvN分别表示光伏系统的输出功率变化值和额定值为光伏系统输出功率变化量对应的MGP电动机电磁转矩变化量的标幺值。

从MGP的直流电压反馈控制策略和电气-机械模型可知，下垂控制的实现需将MGP转子转速偏差值与下垂控制系数Kpv乘积作为偏差信号施加到光伏直流母线电压参考值上，经过PI控制和SPWM调制后改变变流器的开关频率，进而控制输出到SM电磁转矩的大小，最终使得光伏系统的功率输出能响应电网频率变化，由此可得如图4所示的MGP的基于PV下垂控制的直流电压反馈控制结构图。

图4 基于PV下垂控制的直流电压反馈控制结构图Fig.4 DC voltage feedback control structure based on PV droop control

需要注意的是，为保证光伏系统能稳定运行，还要控制光伏直流母线电压的调节范围不超过运行点稳定区域，因而需要对下垂控制输出的电压调节信号设置限幅，当光伏系统处于满发状态，下垂控制不再对电网频率进一步的跌落作出响应。

3 仿真分析

为验证MGP的惯性响应能力，并对比控制策略改进前后光伏经MGP并网的一次调频能力，以及比较控制策略改进后光伏经MGP并网与光伏采用虚拟惯量控制+下垂控制并网的频率调节能力，本文运用PSCAD/EMTDC电磁暂态仿真软件进行算例分析，搭建了如图5所示的经典3机9节点仿真模型。系统关键参数如下：同步机组G1/G2/G3出力150 MW，光伏系统最大输出功率110 MW，G1/G2/G3的惯性时间常数M=5，MGP惯性时间常数MMGP=3.3，工频50 Hz。光伏系统运行在BUS5，仿真中可以分别切换光伏系统采用直接并网和MGP并网两种并网方式，在系统稳定运行后设置大容量负荷突然切入/退出故障，对比光伏系统在两种运行方式下的调频情况。

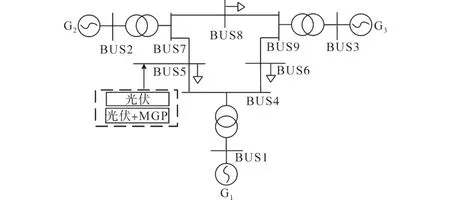
图5 经典3机9节点仿真系统Fig.5 Classical 3 machines and 9 nodes simulation system

3.1 MGP惯性响应能力与控制策略改进前/后一次调频能力的验证

设光伏系统初始阶段处在减载运行情况下（减载储备15 MW），在60 s时，BUS6突然切入/切除40 MW负荷致使电网频率突变，对比光伏系统驱动MGP并网在有/无下垂控制下的并网输出功率和电网频率的变化情况，系统仿真结果如图6所示。

图6 系统动态响应比较1Fig.6 Comparison of system dynamic responses 1

由图6的MGP功率响应曲线和系统频率变化曲线可知，未加入下垂控制的MGP在电网频率变化将瞬时释放转动惯量抑制频率跌落，这是MGP自发的惯性响应，但由于光伏系统未参与一次调频，转子在转速恢复过程中会吸收一部分能量，造成一段时间MGP的输出有功功率低于故障前输出水平，不利于电网频率的快速恢复。加入下垂控制后的MGP控制系统可以快速调用光伏的减载储备用于一次调频，在电网突然增/减40 MW负荷的情况下，MGP输出功率也相应增发/减发了故障前约10%的输出功率，承担一部分功率不平衡冲击，降低了电网频率波动过程中的频率变化率，最大频率偏差也分别减小了0.012/0.009 Hz。通过以上分析可知，在一次调频过程中，采用基于PV下垂控制的直流电压反馈控制策略的MGP能快速调动光伏系统的减载功率储备，参与同步机组的功率分配，分担一部分调频压力，有效地增强了电网的频率调节能力，但考虑到不同下垂控制系数Kpv的选取、变换器的功率变化速率限制和光伏实际减载情况的影响因素，控制改进的实际效果会有所不同。

3.2 光伏系统不同并网方式下的调频能力对比

为对比光伏采用虚拟惯量控制+下垂控制并网与采用基于PV下垂控制的直流电压反馈控制策略的光伏经MGP并网的频率调节能力，参考文献[10]搭建了光伏直接并网的一次调频仿真模型。

在图5所示的3机9节点仿真系统中，设置光伏在BUS5并网，在忽略MGP并网的电机损耗情况下，光伏直接并网与光伏经MGP并网的初始阶段输出功率相同，一段时间后，在BUS8设置大容量负荷突然切入/退出故障，观察两种方式下的系统频率响应情况，为保证一次调频调用能量相同，控制仿真中将保持两种并网方式的调频增发/减发功率峰值和故障后稳态功率一致。设光伏系统初始阶段运行在减载情况下（减载储备15 MW），在60 s时，BUS8突然切入/切除80 MW负荷致使频率下降，对比光伏直接并网与光伏经MGP并网两种方式下的并网输出功率和电网频率的变化情况，系统仿真结果如图7所示。

图7 系统动态响应比较2Fig.7 Comparison of system dynamic response 2

由图7的光伏输出功率响应曲线和频率变化曲线可知，即使两种并网方式增发/减发的有功功率最大值相同，但由于MGP旋转转子无延时的惯性响应，在电网负荷突变后的最初阶段，其与虚拟惯量+控制相比，有功功率响应速度更快，频率变化率更小，并且光伏采用虚拟惯量控制的响应时延间接导致最后的频率偏差幅值大于光伏经MGP并网的频率偏差幅值。仿真结果表明，在相同下垂控制作用效果下，MGP真实的惯性响应对电网频率支撑能力的提升效果要优于光伏直接并网下的虚拟的惯量响应。

4 控制改进效果的实验验证

为验证控制策略改进效果，搭建了如图8所示的5 kW实验平台，系统详细参数如下：光伏模拟器额定容量10 kW，变频器额定容量30 kW，MGP额定容量5 kW，可编程负载最大容量30 kW，电网频率50 Hz。实验中光伏模拟器有足够的减载储备。

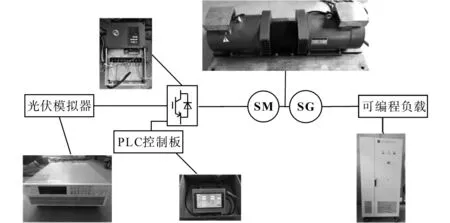
图8 MGP实验平台Fig.8 Experimental platform of MGP

实验设定可编程负载初始时刻运行在单相600 W功率条件下，并根据光伏运行曲线，设置直流电压反馈控制的参考电压约为570 V，待变频启动MGP至额定转速后，调节设定参考电压与实测光伏直流电压一致后约9.4 s，进行变负载实验。实验分为两次，分别为单相负载600 W突增至700 W和单相负载600 W突降至400 W，并在控制策略中引入下垂控制环（下垂控制系数Kpv取1.5）后重复以上实验，测量到的MGP发电机端的电压频率响应如图9所示。

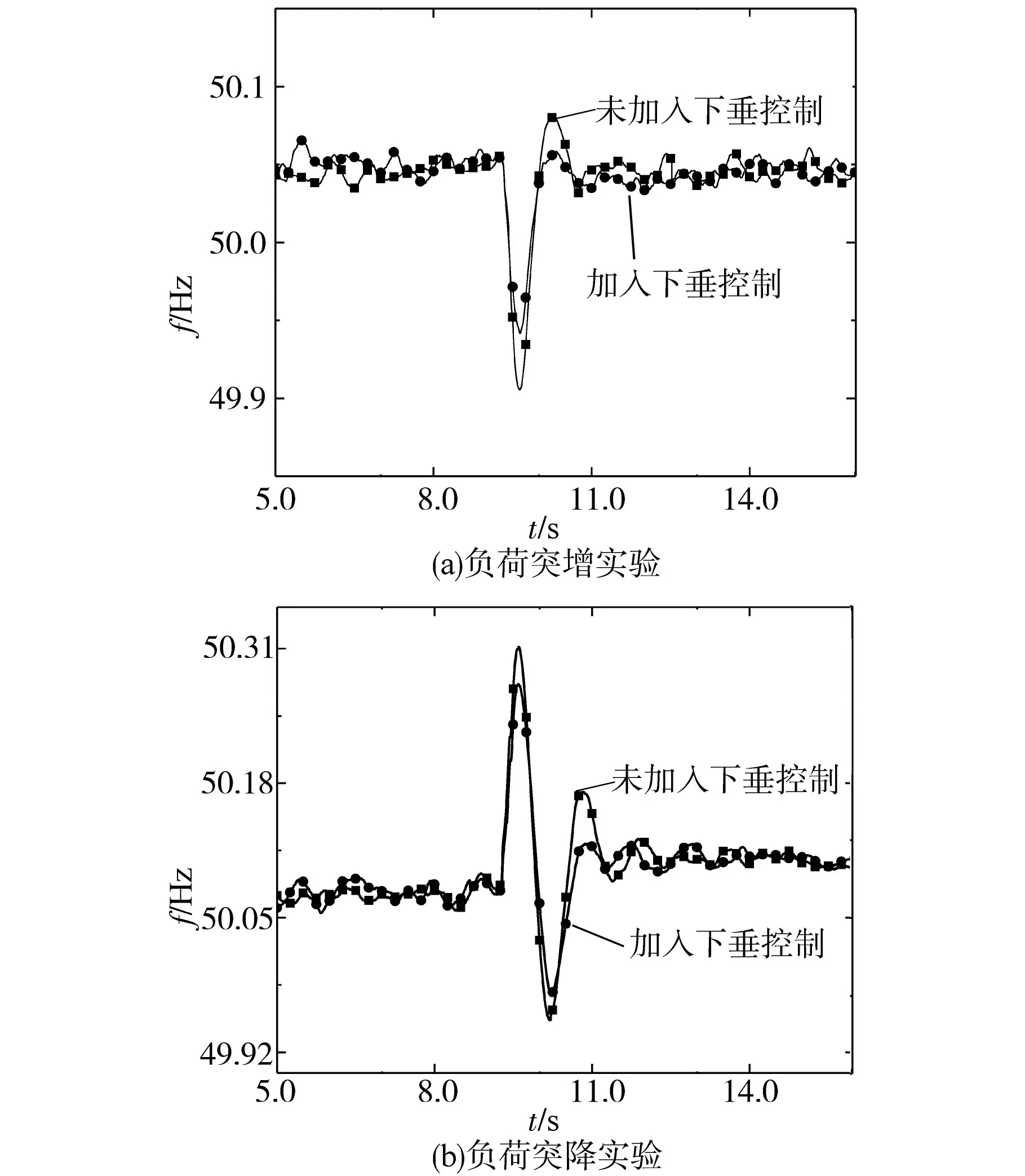
图9 MGP变负载实验Fig.9 Variable load experiment of MGP

由图9的实验结果可知，在引入下垂控制后，负载端负荷发生突变时，光伏系统主动的功率响应能迅速配合MGP参与调频，减小了功率扰动过程中的最大频率偏差以及转子转速恢复至额定值过程中的超调量，因而提升了系统的频率稳定能力。由于实验系统不具有二次调频功能，因此负荷变化后的稳态频率与变化前存在静态偏差。

5 结论

本文提出了一种MGP的基于PV下垂控制的直流电压反馈控制策略，在仿真中实现了MGP惯性响应与光伏系统有功功率响应配合参与电力系统一次调频，有效提高了电网频率调节能力；然后对控制策略改进后的光伏经MGP并网与光伏采用虚拟惯量+下垂控制并网的一次调频能力进行了仿真对比，证明了MGP转子无延时的惯性响应能减小电网频率变化率和偏差幅度，提供更强的频率支撑，并在最后通过实验验证了光伏经MGP并网在控制策略改进后对系统频率支撑能力的提升作用。