多元表征：让数学“看得见”

【摘要】本文基于多元表征教学理念，从图像表征让算理可见、图形表征让知识结构可见、身体表征让度量概念可量可感、言语表征让数学思考听得见、多元表征让数学看得见等多个维度论述降低小学生数学学习难度的实践策略。

【关键词】多元表征 小学数学 可感可见

【中图分类号】G62 【文献标识码】A

【文章编号】0450-9889（2022）10-0091-03

《义务教育数学课程标准（2011年版）》指出：数学是研究数量关系和空间形式的科学。为了便于小学生正确理解抽象的数形概念及关系，小学数学教师需要采用多元表征的方式，让抽象的数学于小学生而言可感可见，帮助小学生降低学习数学的难度，培养学习数学的兴趣，发展学习数学的综合能力。

所谓多元表征，通俗地说就是把同一种数学知识（概念、规律等）通过不同的形式表现出来。“表征”，现代汉语词典解释为“显示出来的现象”“表现出来的特征”。也就是说，表征是一种信息记载或表达的方式，是能把某些实体或某类信息表达清楚的形式化系统以及说明该系統如何行使其职能的若干规则。美国著名数学教育心理学家莱什认为，数学学习中存在图形图表、言语、实物情境、书写符号、教具模型五种表征类型，其中：实物情境指的是解释学习内容或问题情境的实际物品，教具模型指的是显示学习对象的内在关系的具体物，图形图表指的是将数学关系予以具体、形象化表示或推理的图形或图表，言语指的是日常口语和数学的特殊语言、数学专有名词，书写符号指的是一般的书面符号和数学的特殊符号（数字符号、运算符号与关系符号等）。例如，对于“[13]所代表的意义”这种思维层面的学习内容：直呼“三分之一”的音便是言语表征;先把一个规则的图形平均分成3份，涂色表示其中的1份便是图形表征;在实际生活中把3个苹果平均分成3份，告诉别人其中的一份就是“[13]”，这是实物情境表征。其实，关于多元表征的类型划分，在数学界历来仁者见仁智者见智。下面，笔者将结合自身的小学数学教学实践，谈谈多元表征于数学教学的意义。

一、图像表征——让算理可见

算理是计算过程中的道理，回答思维层面“为什么这样算”的问题;算法是人为规定的计算方法，为数学计算提供快捷的操作方法。算理是算法的理论依据，算法是算理的提炼和概括。算法教学时常需要以算理教学为基础。笔者以为，在小学数学教学中，基于小学生的年龄特点和形象思维特征，遵循儿童认知规律，教师可以借助实物、图表或图像表征的方式以及操作、观察等数学实验活动的方法，让学生形象感知数学知识产生的过程，从中理解算理、掌握算法，进而达到让学生既知其然又知其所以然的目的。

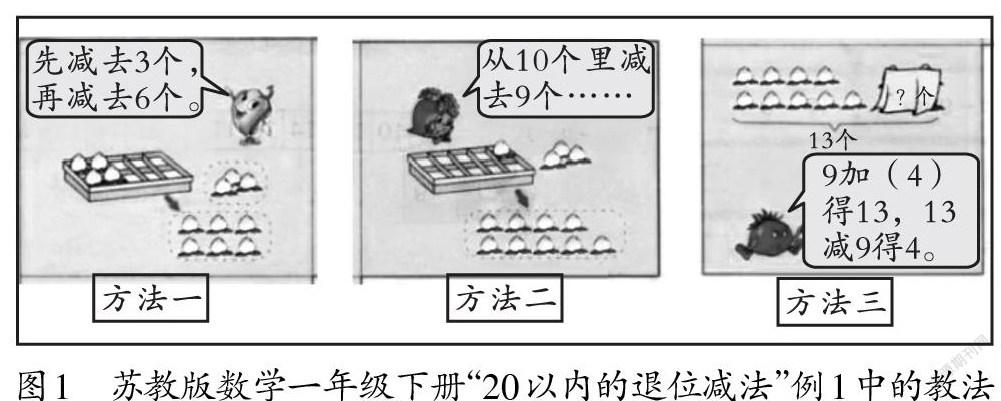
例如，苏教版数学一年级下册第一单元“20以内的退位减法”第一节，教材创设了一个小猴买东西的实物情境：盒子里有10个桃子，外面有3个，小猴要买9个，问还剩多少个。很明显，这是一个“十几减几”的计算问题。怎么减呢？教材中没有陈述“破十法”或“平十法”的计算方法，而是直接呈现了如图1所示的三种图像表征，暗含了三种不同的计算方法。“方法一”的图像中：盒子外有3个，又取出了6个，盒子内还有4个，此图像可以看作“平十法”的算理表征，相当于将减数9分成3和6，先去掉盒子外的3个，就是13-3=10（个），此所谓“平十”;再从盒子里的10个中去掉6个，于是得出结果10-6=4（个）。方法二的图像中：直接从盒子里的10个中拿去了9个，于是10-9=1（个），完成了交易，此所谓“破十”;再将盒子里剩下的1个与盒子外的3个合在一起，便是最终剩下的桃子数，即1+3=4（个）。方法三的图像中：把退位减法直接变成进位加法，体现了“减法是加法的逆运算”的算理。教学实践中，教师如果直接告诉一年级的小学生什么是“破十法”和“平十法”，再让学生去运用这些方法解决问题，因算法过于抽象，很容易“破坏”小学生的学习兴趣，导致小学生的学习困难;运用教材中的图像表征形式展开教学，学生选择算法、积极参与学习活动的热情高涨。在本课中，大多数学生更乐于选择方法二“破十法”，少数学生选择了方法一“平十法”，选择方法三的学生少之又少。

以上退位减法的算法学习，借助数学知识的图像表征方式，既能让学生形象地感知到方法形成的动态过程，又能让学生经历“不仅知其然而且知其所以然”的算理阐释过程，很好地培养了学生的数学思维。

二、图形表征——让知识结构可见

复习课承载着知识的回顾与整理、实现学生知识建构与生长的独特功能。怎样让学生在“温顾”中“知新”，突破“一问一答再巩固”的复习课模式？笔者尝试带领学生用思维导图等图形表征方式整理和沟通相关知识，取得了较好的实践效果。长此以往，学生到高年级以后，便可以自主运用教师教给的图形表征方法，整理跨单元、跨年级的数学知识了。

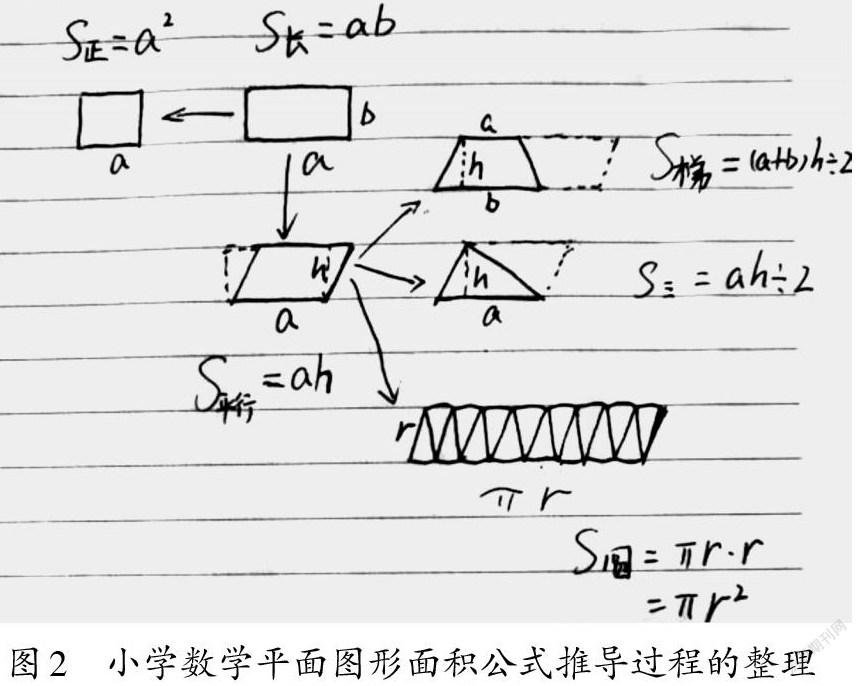
例如，学生在学完正方形、长方形、平行四边形、梯形、三角形、圆形等平面图形的面积计算公式及推导过程之后，在教师指导下，自主整理相关知识、沟通其间关系，构建了如图2所示的图形表征。

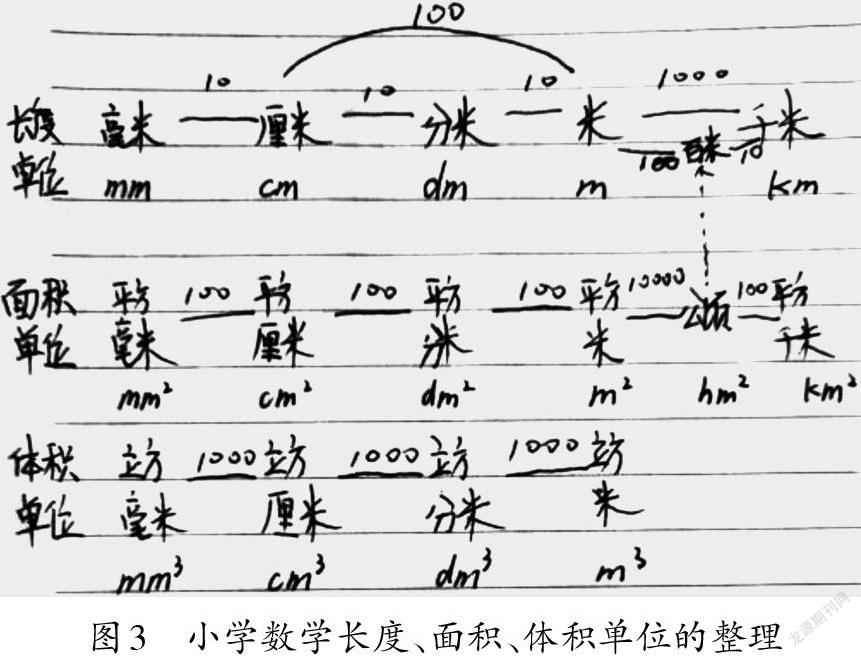
学生掌握了方法，还可以如图3所示自如地应用图形表征方式，整理长度单位、面积单位、体积单位等知识。在图3的图形表征中，学生能用文字和符号表示各个单位，并沟通了单位间的内在联系——表达出了相邻单位间的进率，还补上了与面积单位公顷相对应的长度单位“百米”，知识整理的水平达到了自然生成的境地。

三、身体表征——让度量概念可量可感

身体表征是基于自己的理解和想象，用身体或肢体的姿势或动作来呈现内在思维的一种表征方式。度量指的是运用一个带单位的数值刻画某种物体某类属性，赋予这个数值特殊意义的行为，比如度量物体的长度、面积、体积、质量、时间等。度量是人类创造出来的一种数学语言，是人认识、理解和表达现实世界某一类特征的工具。正如庞加莱所说：“如果没有测量空间的工具，我们便不能构造空间。”小学数学图形与几何领域中的度量教学分散在计量单位的认识与换算、平面图形的周长与面积、立体图形的表面积与体积、不规则图形的面积和体积当中。为了培养学生的几何直观学科素养，教师在实施度量教学时，可引导学生借助身体表征的方式去认识、理解和表达现实世界。

例如，在学习长度单位时，借助“身体尺”（如图4），学生可以形象具体地把握外在的世界。这样的“身体尺”还有很多，比如：1厘米约等于大拇指指甲的宽;1分米约等于大拇指和食指张开的距离;1米约等于二年级班上个子较矮的小朋友两手张开的距离，也称为一庹;1平方厘米约等于大拇指的指甲盖的面积;1平方分米约等于两只手的大拇指和食指张开所组成的图形的面积;1平方米约等于同桌两人伸出双臂围成较大的图形的面积以及两个小朋友双脚张开面对面坐在地上所围成的图形的面积……

“我听见了就忘记了，我看见了便记住了，我做过了就理解了。”学生用“身体尺”表达自己对常见的长度、面积单位的理解与记忆，可以让度量概念可量可感。

四、言语表征——让数学思考听得见

爱因斯坦说过：“一个人的智力发展和形成概念的方法在很大程度上是取决于语言的。”核心素养导向下的数学课堂教学，教师应有意识地引导学生学会用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界。

例如，教师执教苏教版数学二年级上册第五单元“厘米和米的认识”一课，在教材所呈现的一个测量线段长度的图示中，学生给出了两个答案，一个说是11厘米，一个说是8厘米，教师没有直接评判二者的对错，而是与学生展开了下面的课堂对话。

师：现在我们有两种意见，到底谁说得对呢？请你说出理由。

生1：我觉得是11厘米，因为终点是11厘米。

生2：我不同意！这条线段的起点是3厘米，从3厘米到4厘米是1厘米，从4厘米到5厘米是1厘米，这样数下去，一共有8个1厘米，就是8厘米。

师：现在你们觉得谁的说法是正确的？

生3：第二个的说法是正确的。因为测量线段的长度，不能光看终点，还要看它的起点是不是在“0”处。如果是从“0”开始的，终点是几就是几厘米;如果起点不在“0”处，可以像刚才那位同样那样一段一段地数，还可以直接用终点的数字减去开始的数字。

学生对知识的理解可以用多种方式表征，但言语表征在形成概念的方法中不可或缺。言语表征，可以让学生的数学思考“听得见”。

五、多元表征——让数学“看得见”

实际教学中，教师常常要用到多元表征。运用多元表征推进课堂教学，要特别注意沟通不同表征形式之间的内在联系，让学生可以从不同角度理解和表征数学知识的本质。

例如，执教苏教版五年级下册认识偶数的教学内容：可以用文字的方式表征——“能够被2整除的整数”;可以用图形表征——把实物图像两个两个地圈起来;可以用符号表征——写作“2a，a是大于零的整数”;还可以用数据表征——2、4、6、8、10……多种方式表征，可以帮助学生建构偶数的丰富表象，沟通其内在联系——“2的倍数”，揭示概念的本质。

如果说数学理解是内化和建构的过程，那么数学表达就是外化和应用的过程。数学的多元表征，既要注重数学知识的内化，构建内在表征的“关系网”，又要注重数学能力的外化，在发展学生思维能力和数学语言表达能力的同时，进一步发展学生的问题解决能力。

例如，执教六年级上册“解决问题的策略”例1（如图5），教师放手让学生自由表达看法，学生悄然使用了假设法，呈现了多种解决问题的方式：有的用实物演示，直观形象;有的用图形表征，或者把图形变成线段表征;有的迁移比的思想并列式;有的类比方程的思想并列式;有的同化分数的思想并列式。

在实物、图形、线段三种表征中，可以发现学生共同的思维轨迹：将一个小杯的容量看作单位“1”，大杯容量就是“3”，假如把1个大杯换成3个小杯，这样720毫升的果汁就倒满了9个小杯，用720÷9便可以算出小杯的容量，再由小杯的容量算出大杯的容量。在比的思想的算式表征中，学生把“小杯容量是大杯的[13]”转化为比的思想，即“大杯与小杯容量之比是3∶1”，假如把1个大杯换成3个小杯，这样720毫升的果汁就倒满了9个小杯，用720÷9可以算出小杯的容量，再由小杯的容量可算出大杯的容量。在方程思想的算式表征中，学生把小杯的容量设为x毫升，则大杯的容量就是3x毫升，列方程为6x+3x=720，于是问题解决。同样的题目，学生解决问题的策略是一致的，但方式方法各不相同，展現了他们多元的知识表征方式和思维风格。

多元表征，让算理、建构、度量、思维可感可见，可有效培育和发展学生的数学学科核心素养。

参考文献

[1]李连仓.多元表征：赋予学生数学学习自然生长的力量[J].数学教学通讯，2019（31）：21-22.

[2]潘香君.例谈数学表征的教学价值.教育视界，2021（23）：66-68.

[3]席爱勇.数学多元表征：让概念形成过程“看得见”.小学教育教学，2017（9）：65-67.

[4]刘克臣.基于整体把握视角下的小学数学度量教学.中小学数学，2019（4）：9-11.

作者简介：倪若琳（1995— ），江苏苏州人，小学二级教师，研究方向为小学数学教学。

（责编 白聪敏）