基于MGPI模型的SMA柔性驱动自适应NN控制
冯 颖,梁明威
(华南理工大学自动化科学与工程学院,广东广州 510640)
1 引言
形状记忆合金(shape memory alloy,SMA)是一类通过温度变化实现输出形变的智能材料,具有高功率密度比、噪声小、体积小及质量轻等优势,其超弹性的形变特性可作为类人肌肉驱动部件实现柔顺驱动,逐步应用在微型机器人、智能人工肌肉和微创手术机器人等[1-2]领域.
随着对SMA材料及其应用研究的深入,在作为柔性驱动部件使用时,驱动性能的提升主要受到材料和外载荷特性的限制.SMA在温度变化的激励过程中实现微观奥氏体相(Austenite)和马氏体相(Martensite)的相互转化,其热力学迟滞响应造成输入输出信号之间表现出强饱和的回滞非线性.此外,SMA驱动部件在加入外载荷后,载荷变化也对SMA的动力学特性带来影响,从而使得输出行为更为复杂.因此如何结合SMA的材料特性,通过控制策略改进驱动性能,成为SMA柔性驱动部件性能提升的关键[3-4].
与其他智能材料相比,SMA柔性驱动部件中非孪晶马氏体与奥氏体转换产生的超弹性特性表现出强饱和不对称的回滞特性.为了精确表征SMA材料的输入输出关系,国内外众多学者开展了相关建模研究.例如基于SMA材料的相变机理,提出的物理模型有Tanaka模型[5]、Liang-Rogers模型[6]和Brinson模型[7]等,但模型中的物理参数难以确定,并且模型参数对环境敏感,难以实现对回滞特性的精确表征.针对物理模型的局限性,唯象回滞模型得到了广泛研究,例如Preisach 模 型[8]、Krasnoselskii-Pokrovskii(KP)模型[9]、Duhem模型[10]及Prandtl-Ishlinskii(PI)模型[11]等.此外,还利用神经网络方法对回滞进行建模[12].
针对SMA材料中强饱和回滞非线性,如何实现对其精确表征成为回滞建模研究的关键.例如传统的PI回滞模型无法表征此饱和特性,已有学者通过拓展传统的Play算子得到广义Play算子,建立一类广义PI(generalized prandtl-ishlinskii,GPI)回滞模型[13],实现对SMA驱动部件中强饱和回滞驱动特性的精确描述.但此建模策略在应用到闭环控制策略研究中,因其算子中的包络函数和输入形状函数的非线性特性,无法直接实现控制器设计,这使得直接基于GPI回滞模型的控制策略设计存在困难[14].
为了利用GPI回滞模型表征SMA柔性驱动部件的优势,并有效解决基于GPI回滞模型的闭环控制系统控制器设计问题,本文在GPI回滞模型的基础上,通过改进GPI模型中的形状函数(shape function),建立了一种修正的GPI回滞模型,即(modified generalized prandtl-ishlinskii,MGPI)回滞模型.MGPI回滞模型不仅能够有效表征SMA柔性驱动部件中的强饱和非对称回滞特性,还通过改进GPI回滞模型的输入形状函数,使其具备线性项,从而为后续控制器设计奠定基础.
随着智能材料驱动部件在各个领域的推广应用,通过控制算法来提升智能材料驱动部件驱动性能也得到了国内外学者的高度关注.针对SMA柔性驱动部件,如何有效抑制内部的强饱和回滞非线性对驱动精度的影响,改善系统动态特性,成为SMA柔性驱动部件控制设计的关键.例如,基于回滞逆模型补偿的前馈反馈复合控制[15-16]、H∞鲁棒控制[17]、自抗扰控制[18]、鲁棒滑模控制[19]、基于反步法的自适应控制[20-22]及神经网络控制等等[23-24].其主要的设计难点在于回滞的多值性和不可微特性,使得常规控制策略无法直接应用于控制器设计,因此如何有效利用建模策略来精确表述回滞特性并基于建模结果设计控制算法,成为以SMA柔性驱动部件为代表的智能材料控制设计的难点.
本文重点研究SMA驱动部件在带载条件下改善驱动性能的控制策略研究.基于所提出的MGPI唯象模型,采用自适应神经网络来有效解决系统模型中的未知参数和外部扰动的影响,并能保证系统全局稳定的前提下闭环稳定和输出跟踪特性.主要创新点如下:1)在SMA迟滞建模方面,提出带有线性输入函数的MGPI回滞模型,所提模型参数辨识难度小,也为后续控制器设计提供便利;2)研究负载变化对SMA回滞特性的影响,将负载影响因素解析性地体现在回滞模型参数中,进而将SMA驱动系统表征为一类参数不确定的系统;3)为了改善强饱和回滞及负载的影响,本文提出了基于神经网络的自适应控制算法,以提升SMA柔性驱动部件在复杂操作环境下的驱动性能.
2 SMA柔性驱动部件工作特性
2.1 实验平台
为了有效验证SMA柔性驱动特性,如图1所示,带载SMA驱动实验平台由SMA丝,热电模块,热电模块驱动器,激光位移传感器和dSPACE实时仿真系统组成.带载驱动部件如图2 所示.通过脉冲宽度调制(PWM)电压的方式来调节热电模块的温度变化,从而实现驱动SMA丝伸缩变化.
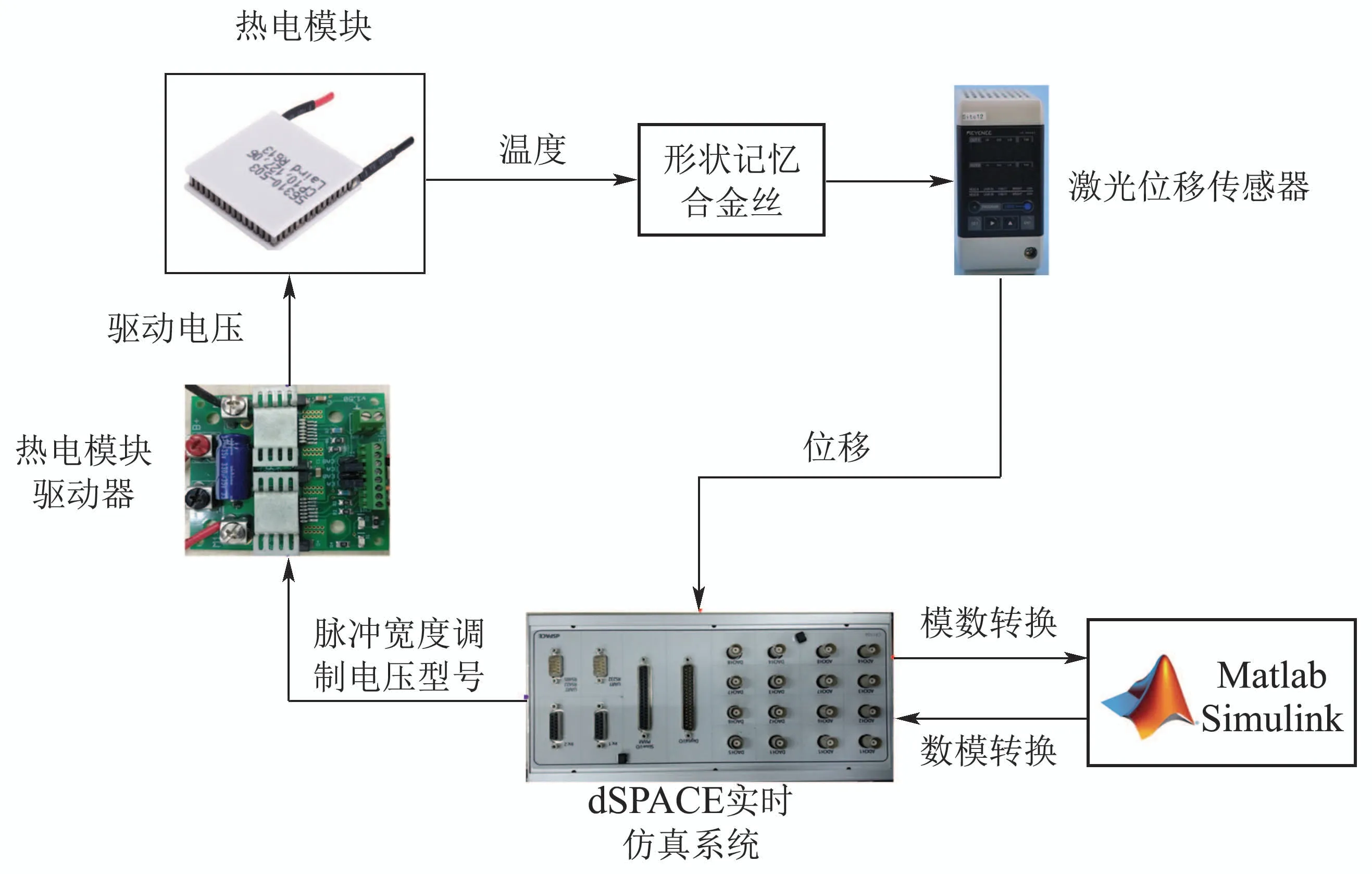
图1 SMA驱动平台结构示意图Fig.1 Schematic diagram of the structure of the SMA actuating platform

图2 带载SMA驱动部件平台Fig.2 Experimental device of SMA actuating platform
2.2 带载SMA驱动部件的工作特性
为了分析SMA驱动系统的回滞特性,实验考虑两组工作状态:第1组为负载不变(负载质量为1.6 kg),PWM电压信号占空比设定为50%,65%,80%,实现输入信号频率变化;第2组为输入电压信号占空比不变(占空比为50%),负载设定为1.6 kg,1.7 kg及1.8 kg,实现载荷变化.其中施加在热电模块上的PWM电压信号的占空比正比于SMA丝驱动温度的变化率.实验结果如图3-4所示.结果表明,SMA驱动部件的输入输出驱动特性具有强饱和非对称特征的回滞特性,且此回滞特性与载荷量和热电模块温度变化均有关.
注1根据图3-4所示的实验结果来看,载荷固定输入信号频率变化时,受到奥氏体相和马氏体相相互转化过程的影响,SMA驱动部件的输出特性受到输入信号频率的影响,呈现非对称性,但实际输出幅值变化不大;载荷变化时,同时也改变了SMA驱动部件内部的动态特性,造成SMA驱动器输出信号的幅值随着载荷的增大而减小,呈现出载荷相关性,因此有必要研究带载条件下SMA驱动部件性能提升的相关策略.
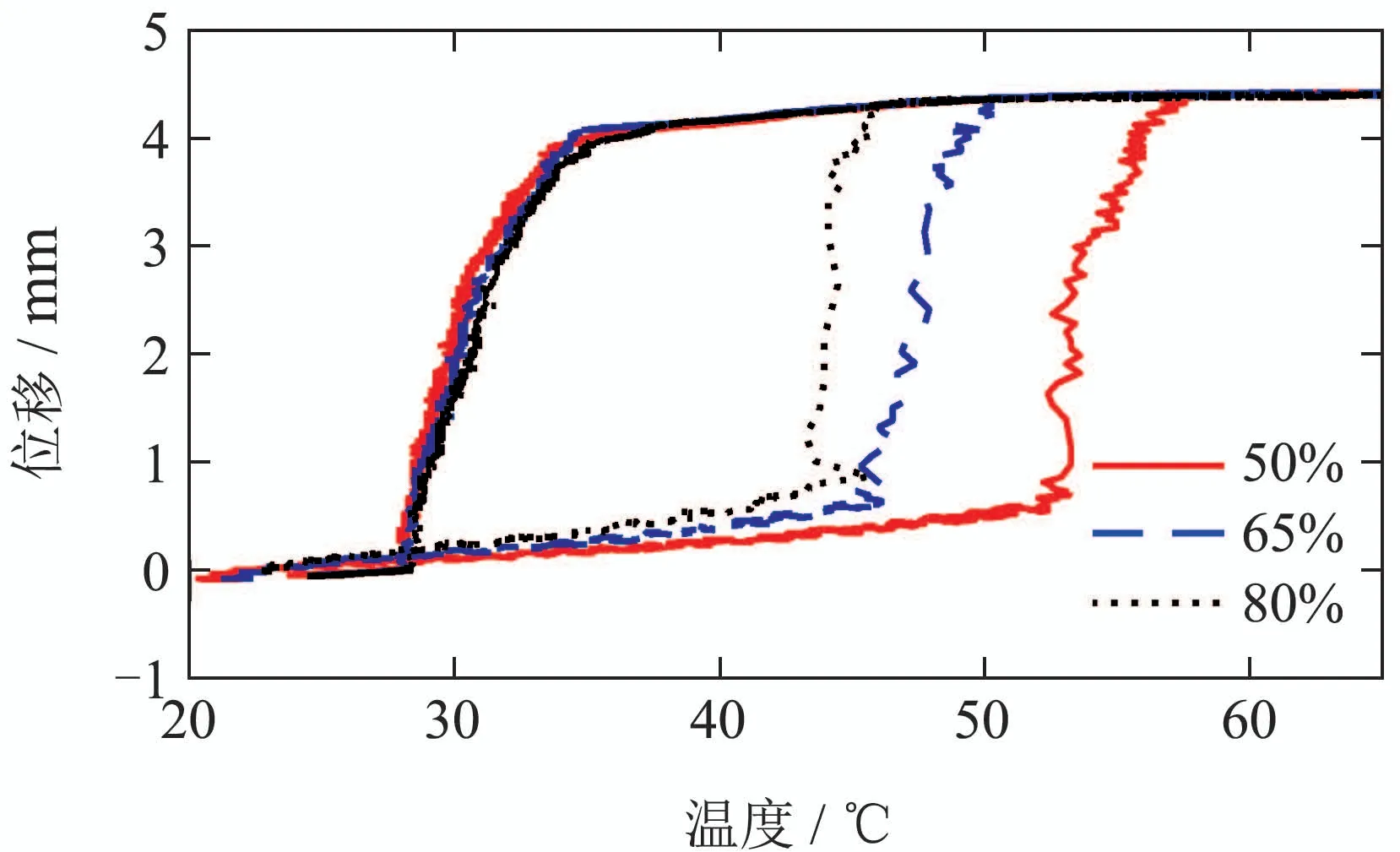
图3 SMA驱动器带载条件下输入输出特性(输入频率变化)Fig.3 Input-output characteristics of the SMA actuators under fixed load with variable input duty cycle
3 SMA柔性驱动建模
3.1 SMA驱动系统数学模型
为了能够有效表征SMA丝在带载条件下的输出特性,在本文中采用MGPI回滞模型来表征带载条件下的SMA驱动部件中的回滞特性.为了说明MGPI回滞模型在控制设计上的便利性,本文首先介绍一种GPI回滞模型.
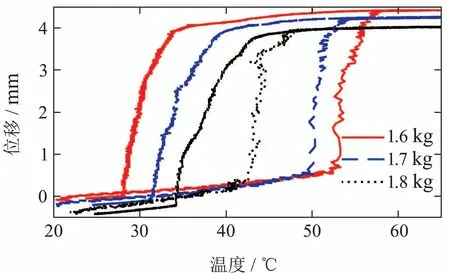
图4 SMA驱动器带载条件下输入输出特性(载荷变化)Fig.4 Input-output characteristics of SMA-based actuators under variable load with fixed input duty cycle
3.2 GPI回滞模型
基于经典的Prandtl-Ishlinkii回滞模型,GPI回滞模型通过拓展经典Play算子为广义Play算子,并通过输入形状函数的拓展,实现对强饱和非对称回滞特性的表征[25].GPI 回滞模型的离散形式定义为
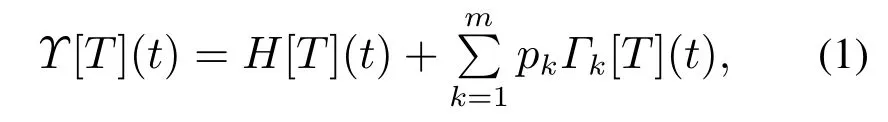
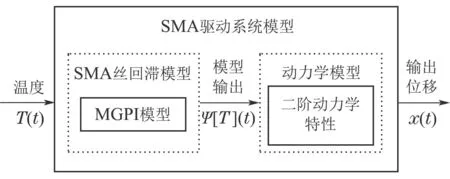
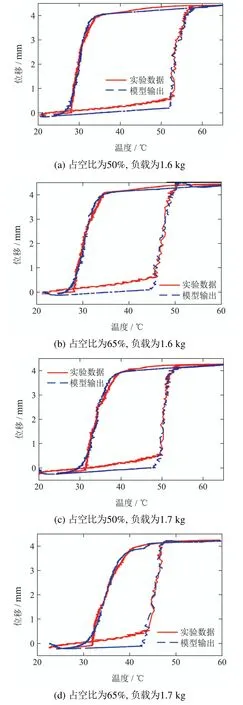
其中:T(t)为为GPI回滞模型的输入;Υ[T](t)为GPI回滞模型的输出,Γk[T](t)是广义Play算子,pk >0为算子密度函数,m是广义Play算子数量;H[T](t)为输入形状函数,满足非负的Lipschitz连续函数属性.
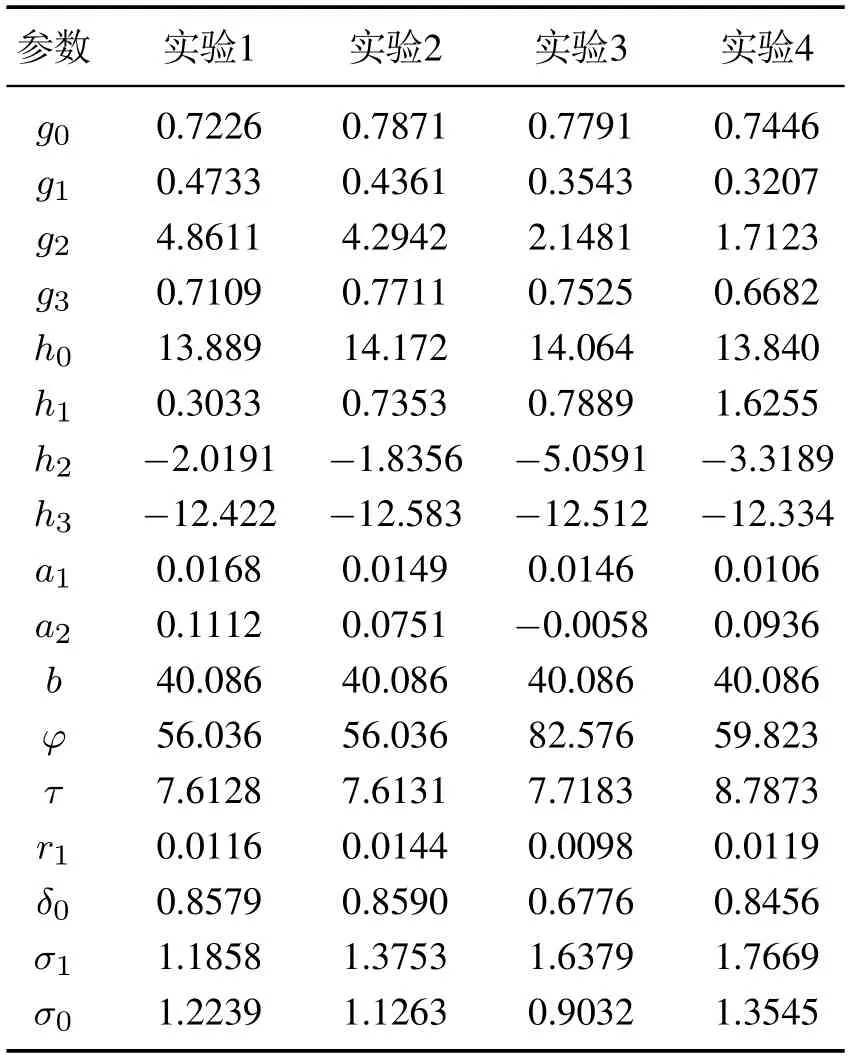
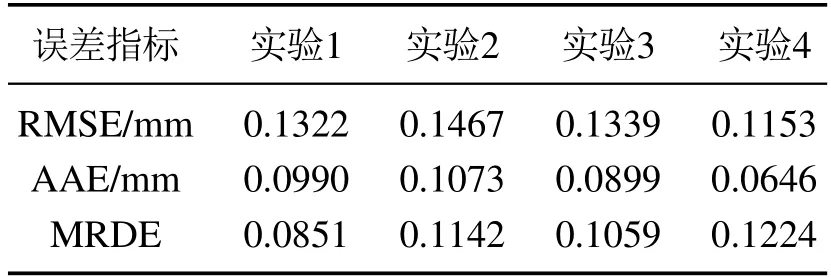
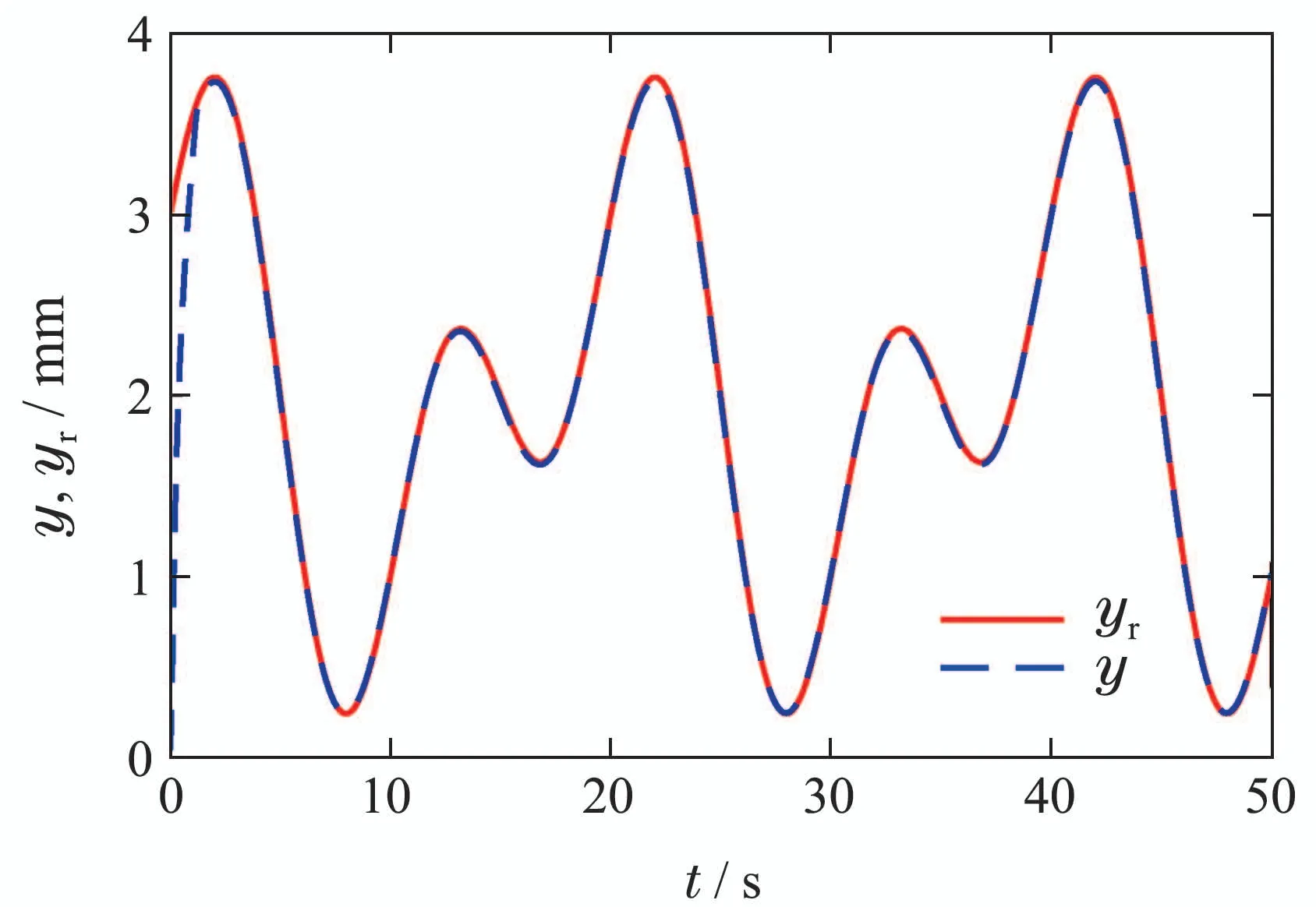
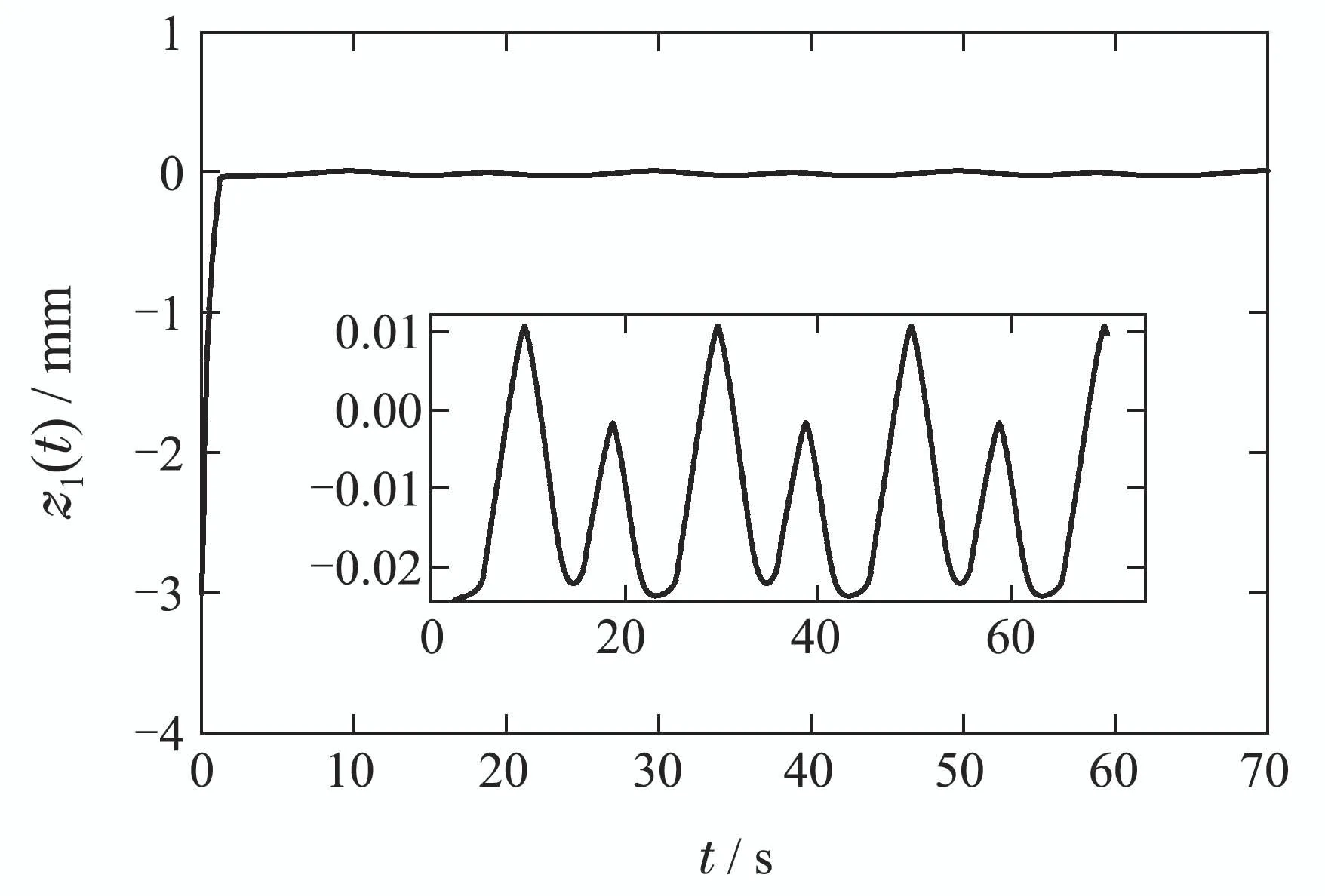
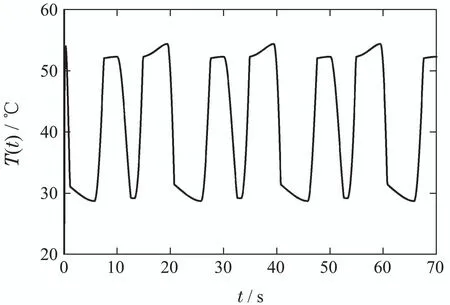
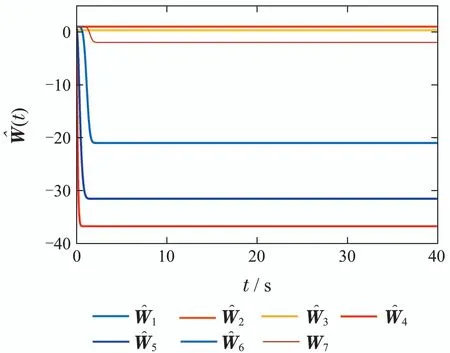
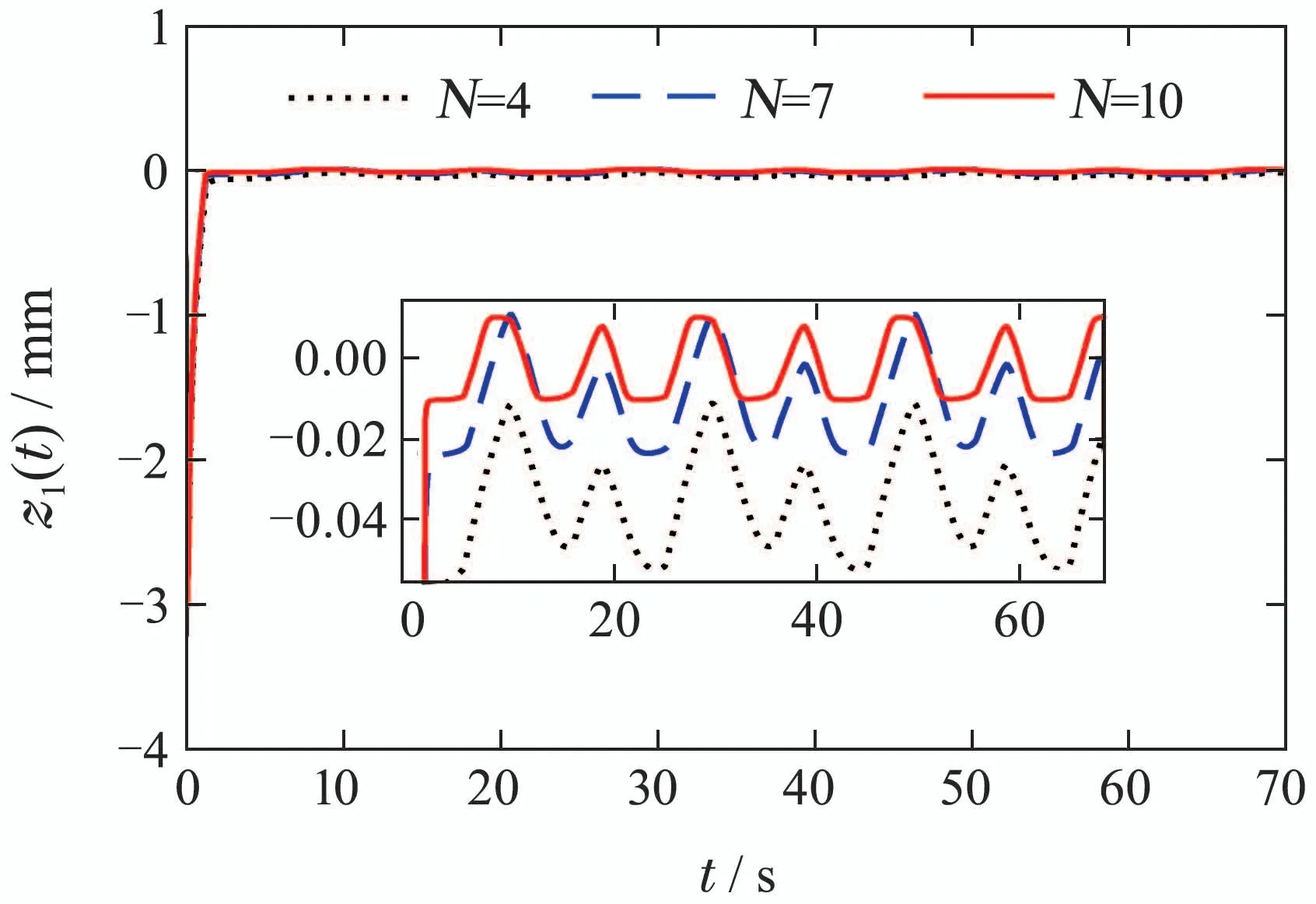
假设任意时刻的输入信号在时间域[0,tE]上是连续函数,时间域[0,tE]可被划分为N个子区间0=t0 rk(k=1,···,m)为正常数.算子权重pk定义为pk=φe−τrk,其中φ和τ为常数;Λl(T)和Λr(T)为GPI回滞模型的包络函数(envelop function),其需具备如下属性:1)包络函数需满足Lipschitz连续;2)广义算子的最大最小值依赖于包络函数. 为了表征强饱和特征的回滞非线性,在文献[25]中,输入形状函数H[T](t)选为 其中:k0,k1,k2,k3,w0,w1,w2,w3为常数. GPI模型虽然可以有效表征强饱和回滞非线性特性,但其模型结构中输入形状函数中无输入信号的线性项,这使得控制算法设计无法直接应用于系统,增加了控制器设计的难度.为了解决此设计难点,本文在GPI回滞模型的基础上提出了一种改进型的GPI回滞模型(MGPI模型),具体定义如下: 类似的,T(t)为为MGPI模型的输入;Ψ[T](t)为MGPI模型的输出信号;Γk为广义Play算子,定义见式(2);pk>0为算子密度函数,定义见式(1);m是广义Play算子数量,a1,a2及b为设计常数.其中b值的选取可以调整广义Play算子的对称性,从而实现MGPI回滞模型对对称或非对称回滞特性的描述. 为了表征SMA丝中的强饱和回滞特性,选取式(3)中的Λl(T)和Λr(T)为如下的双曲正切函数: 其中:g0,g1,g2,g3,h0,h1,h2,h3是常数. 根据文献[20,26]中对SMA的工作特性分析可知,系统动力学模型可以用二阶线性系统来表征,即 其中:σ1,σ0,δ0是常数,x(t)为SMA驱动器的输出位移,Ψ[T](t)是MGPI模型的输出. 基于MGPI回滞模型,在本工作中,将采用此模型来表征带载环境下的SMA驱动部件工作特性.同时考虑SMA驱动部件的动态特性,如图5所示.其解析模型由SMA丝回滞模型和动力学特性串联的结构组成,输入为温度T(t),MGPI回滞模型的输出为式(5)中定义的Ψ[T](t),其也作为SMA驱动器动力学特性的输入,其输出为驱动器的驱动位移x(t). 图5 SMA驱动器模型结构Fig.5 Model structure of the SMA actuators 注2在GPI回滞模型中,为了能够描述SMA强饱和特性,其输入形状函数H[T](t)往往选取为非线性函数,如双曲正切函数等,对非对称特性的表征是通过修改包络函数来实现,此方案虽然能对强饱和回滞非线性实现精确描述,但在控制策略设计时,因其无输入信号的线性项,造成控制算法设计困难.所提的MGPI回滞模型,在输入形状函数H[T](t)中引入输入信号的线性项,在包络曲线的设计中实现对强非线性特性的表征,并引入参数b实现对回滞对称性的调整.MGPI回滞模型在保证对SMA驱动部件中强饱和非对称回滞非线性精确描述的前提下,为后续控制器设计提供便利. 为了有效说明MGPI模型对SMA驱动器在带载条件下实际输出特性表征的精确性,在本研究工作中,选用占空比为50%和65%,负载为1.6 kg和1.7 kg的实验条件进行测试.其中待辨识参数为 采用遗传算法进行参数辨识,表1为4次测试辨识结果,其中实验1测试条件为占空比为50%、负载为1.6 kg;实验2测试条件为占空比为65%、负载为1.6 kg;实验3和实验4的测试条件分别为占空比为50%、负载为1.7 kg和占空比为65%、负载为1.7 kg.根据辨识结果得到的模型输出和实验测量输出对比结果如图6所示.对比结果说明所提建模策略能够有效表征带载条件下的SMA驱动部件的实际输出特性. 图6 带载条件下的MGPI回滞模型输入输出特性与SMA驱动器实验数据对比Fig.6 Comparisons of output-input responses between the proposed MGPI model and the measured data of the SMA actuators with load 表1 模型参数辨识结果Table 1 Model parameter identification results 为了进一步描述建模的准确度,如表2所示定义了3种误差指标函数:均方根误差(root mean squared error,RMSE)、平均绝对误差(average absolute error,AAE) 和最大相对位移误差(maximum relative displacement error,MRDE).表中的符号定义如下:yo(i)为采集到的实验数据,yd(i)为MGPI回滞模型的输出,L是数据点的数目.表3为前述四组实验条件下的误差分析结果.根据多种误差对比结果也可知所采用建模方法的有效性. 表2 误差指标函数的定义Table 2 Definition of error functions 表3 辨识结果的误差指标Table 3 Identification error index 通过对SMA带载条件下的输出特性测试可知,其输出精度受到SMA材料内部回滞及负载的影响,表现出复杂的强非线性特性.为了有效处理SMA柔性驱动部件中的非线性特性影响,本文讨论了一种自适应神经网络控制方法来实现对内部强非线性及外部干扰的有效抑制,保证驱动精度. 具体设计流程如下: 根据式(7),SMA柔性驱动部件的状态方程可写为 基于反步法设计控制器,具体步骤如下: 步骤1选取虚拟控制律α1 定理1对于带载SMA柔性驱动系统(10),采用MGPI回滞模型(5)来表征SMA系统中的非对称强饱和特性.基于此系统,自适应控制律设计为式(20)-(21),参数更新律如式(22)-(24),可保证闭环系统全局稳定,且跟踪误差满足:当t →∞,有|x(t)-yr(t)|→π1. 所提的自适应神经网络控制算法实现流程如下: 步骤1确定系统的期望信号yr,设定控制器参数,根据测试环境设定初始状态; 步骤2定义RBF神经网络的基函数为高斯函数,设定神经元个数; 步骤3根据所建立的SMA驱动系统状态方程(10)及定义的状态变换(11)-(12),计算状态变换误差z1和z2.引入函数sgi(zi)和fi(zi),并设计虚拟控制律α1(15); 步骤4根据实际输出与期望驱动信号差对控制器进行更新,其中控制器的控制律T根据式(20)和(21)定义进行更新,所需估计参数采用设计的参数更新律(22)-(24)进行更新; 步骤5返回步骤3. 仿真结果如图7-11所示,图7为闭环系统实际输出跟踪期望输出曲线,实际输出y在2秒后能实现对期望信号的跟踪;图8为实际SMA柔性驱动部件实际输出跟踪误差,跟踪误差为0.67%;图9为闭环系统的控制信号;图10中给出RBF神经网络权值向量的估计值的收敛情况,在实现对期望信号的跟踪后,也收敛到固定值,实现对未知函数的有效逼近;图11给出了三组神经元(N=4,7,10)下闭环系统的跟踪误差(N=4,1.49%;N=7,0.67%;N=10,0.30%),根据测试结果可知,增加神经元的数目可改善系统的控制精度,在实际应用中可根据精度要求来调整神经元数目.根据仿真结果可知,基于所设计的控制器,SMA柔性驱动系统可实现迅速跟踪上给定的期望信号,并保证跟踪误差. 图7 实际输出y与期望输出yrFig.7 Actual output y and desired output yr 图8 跟踪误差z1(t)Fig.8 Tracking error z1(t) 图9 控制信号T(t)Fig.9 Control signal T(t) 图10 权值向量估计值ˆWFig.10 Weight vector estimate ˆW 图11 神经元数目对跟踪误差z1(t)的影响Fig.11 Effects of the neurons number on the tracking error z1(t) 基于SMA材料的柔性驱动部件其输入输出之间表现出强饱和非对称回滞特性,且受到所带载荷变化的影响,限制了驱动性能的提升.为了改进此材料特性上的限制,提高驱动性能,本文结合GPI回滞模型表征强饱和回滞特性的优势,提出改进型的MGPI回滞模型.基于SMA柔性驱动部件的动态特性,实现对SMA柔性驱动部件在带载条件下的动态特性研究.结合系统模型特点,本文结合神经网络逼近策略提出了一种自适应络控制算法,控制器可以有效抑制SMA材料内部的强非线性影响,并在保证闭环系统稳定基础下实现对给定驱动信号的实时跟踪.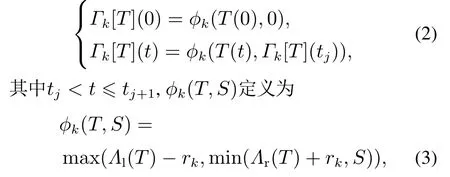
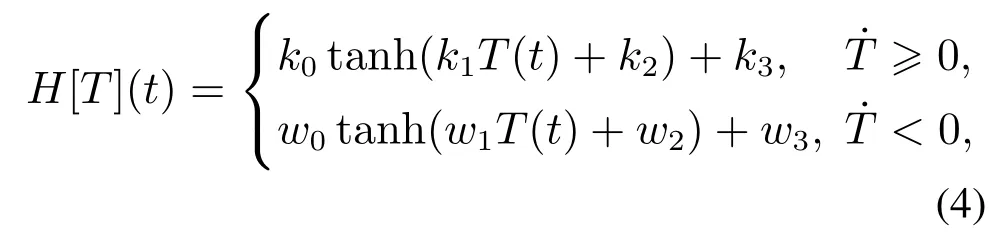
3.3 MGPI回滞模型
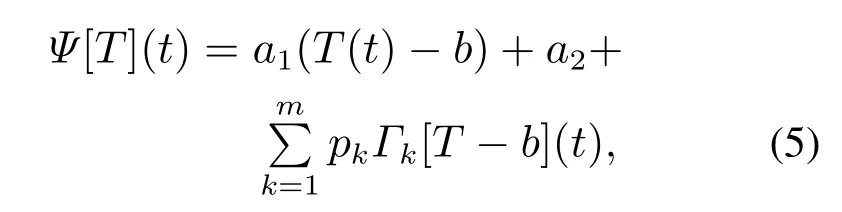
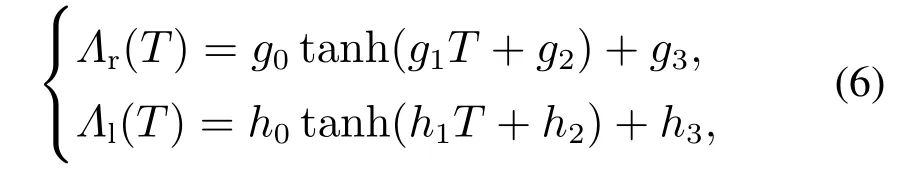
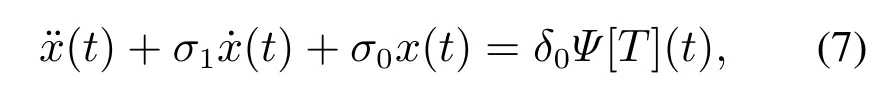
3.4 SMA驱动系统模型辨识
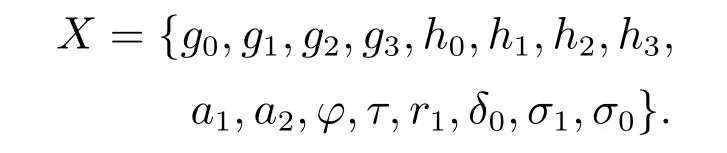

4 自适应神经网络控制设计

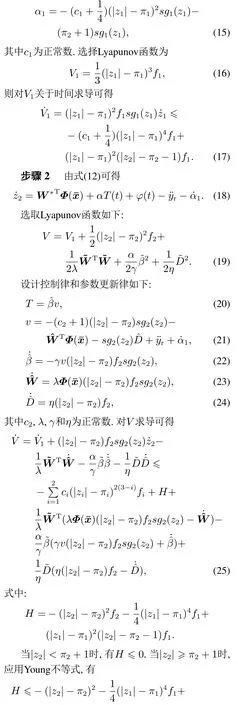


5 仿真验证

6 结论

