含分层复合材料管道中超声导波的模态转换特性研究

石颖颖，赵金玲，杨乐辉,赵建平

(1.南京工业大学 机械与动力工程学院，南京 211816；2.江苏省极端承压装备设计与制造重点实验室，南京 211816)

0 引言

复合材料管道结构广泛应用于军工领域(航空、航天、导弹等)和民用领域(石油、化工、建筑、环保、贮罐等)。复合材料压力容器在传热、传质、反应等工艺过程中，不可避免地会发生损伤，其中分层损伤是层合复合材料中最常见的损伤之一[1-2]。在循环载荷作用下，分层会沿着一定的方向扩展，最终导致材料失效。超声检测可有效地对结构的安全现状进行评估，为及时进行损伤修复以及寿命预估提供依据[3-7]。

超声检测的开展依赖于结构的频散特性研究。20世纪20年代，GHOSH[8]首次根据波在空心圆柱壳中传播的理论基础，推算出其对应的线弹性解，但没有对应的数值分析和试验验证。LIN等[9]以板壳理论为基础，得到了空心圆柱壳中轴对称模态的频散关系。对于多层管道结构，BARSHINGER[10]使用全局矩阵法，推导出导波在多层圆柱壳中的频散方程。半解析有限元方法(Semi-analytical Finite Element Method,SAFE)是分析多层管道频散特性的另一重要方法。NELSON等[11-12]利用半解析有限元法，求解弹性层状正交各项异性板以及圆管结构的弹性波传播问题。HAYASHI等[13-15]基于半解析有限元法，开展了多种波导结构中导波的传播特性研究，包括板、圆管以及铁轨等。最近，HAKODA等[16]提出基于Floquet边界条件的特征频率方法，求解了单层板、单层管的频散曲线。

在复合材料分层损伤的检测方面，SHOJA等[17]使用低频导波对复合材料层压板中的分层检测进行了数值模拟；ALLEYNE等[18]研究了兰姆波与各种缺陷的相互作用，分析了不同兰姆波模态对缺陷的敏感性；GUO等[19]证实了兰姆波可以用于检测层合板中的分层，且分层的深度是影响波传播特性的重要因素；RAMADAS等[20]观察到分层引起的多模态转换现象;SOHN等[21]设计了先进的导波场信号处理方法，检测了复合材料中的分层;GAO等[22]使用电磁超声换能器，对分层结构中的分层进行了有效检测;SOLEIMANPOUR等[23]研究了复合材料层合梁中分层检测的非线性导波方法。

上述文献表明，目前多层复合材料结构频散特性的理论求解方法主要依赖于三维弹性理论的传递矩阵法和半解析有限元法。传递矩阵法可以得到精确的频散控制方程，但当层数增加时，求解超越方程异常困难，且易出现漏根等问题。半解析有限元方法对不同的波导截面具有较大的适用性，但需要编写代码。因此，有必要建立一种高效、易实现的求解方法，对复合材料管道中的导波频散特性进行分析。

虽然目前基于超声导波的复合材料分层损伤检测技术取得了一定的进展，但大多研究集中在复合材料板类结构，对复合管道的分层损伤检测较少。究其原因，发现复合材料管道中的导波传播特性尚不明确，分层损伤对导波的影响机制以及检测原理亟待研究。

为了解决上述问题，本文结合Floquet周期性边界条件和有限元特征频率求解法，高效、简便地分析复合材料管道中超声波的频散特性；进一步从数值仿真角度，针对反射和模态转换两种损伤因子，研究分层损伤对导波传播特性的调制规律，为后续试验研究提供坚实的理论指导。

1 基于Floquet边界条件的特征频率方法

1.1 理论模型

Floquet边界条件通常作用于平行表面，定义为：

udst=usrce-ikF(rdst-rsrc)

(1)

式中，u为位移场；dst，src分别为目标边界、源边界；kF为波数；r为空间位置。

假设一个无限长的管道波导(见图1)，采用Floquet边界条件，将域从图1缩减到图2，用元胞结构进行等效求解。具体原理如式(2)～(10)所示。

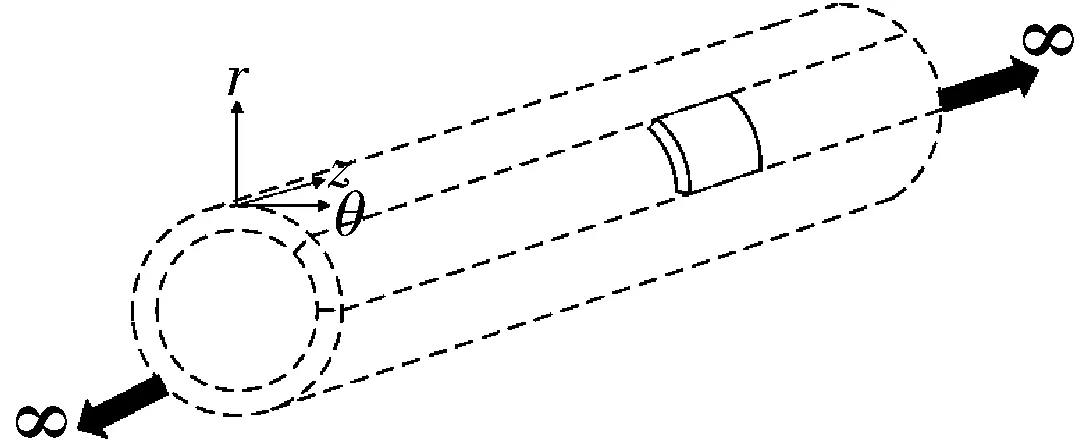
图1 无限长管道示意Fig.1 Infinitely large pipeline

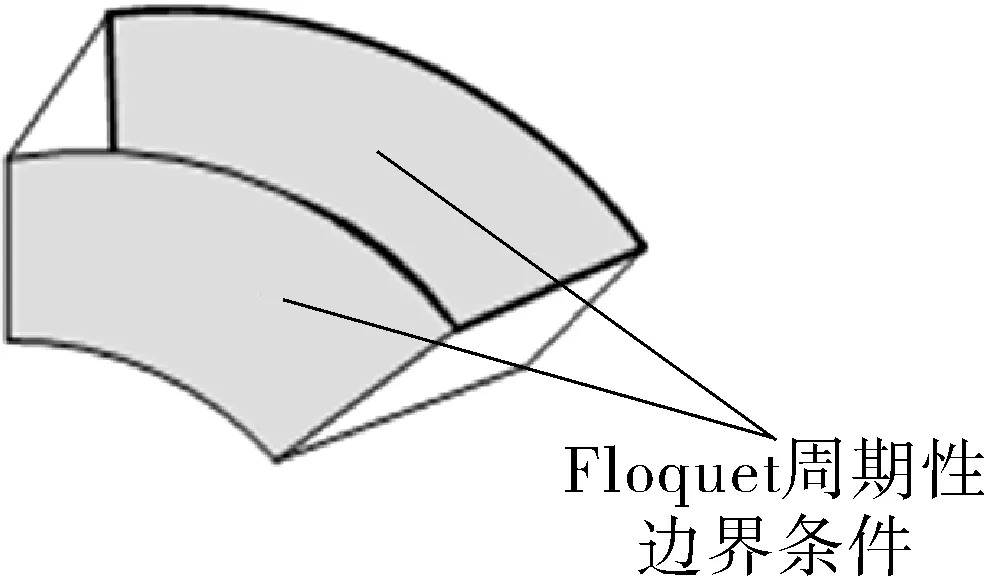
图2 元胞结构与Floquet边界条件Fig.2 Cell structure and Floquet boundary conditions

无限长的管道波导结构的位移为:

u(r,t)=U(r)e-i(mθ+kzz)+iωt

(2)

图2中的元胞结构详细图解如图3所示，几何变量和物理变量的变化如式(3)～(8)所示。

r=r′

(3)

θ=θ′+mθθs

(4)

z=z′+mzsz

(5)

kr=0

(6)

(7)

(8)

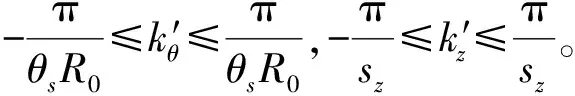
将式(3)～(8)代入式(2)得：

u(r,t)=e-i(k′θmθR0θs+k′zmzsz)U(z′)e-i(mθ′+kzz′)+iωt

(9)

如果e-i(k′θmθR0θs+k′zmzsz)是连续的，则有：

u(r,t)=U(r)e-i(mθ′+kzz′)+iωt

(10)

将式(10)与式(2)对比可知，可以用小的元胞结构代替整个无限大的管道结构(如图3所示)，使得整个管道结构表示为元胞结构的周期性延拓，从而简化计算。

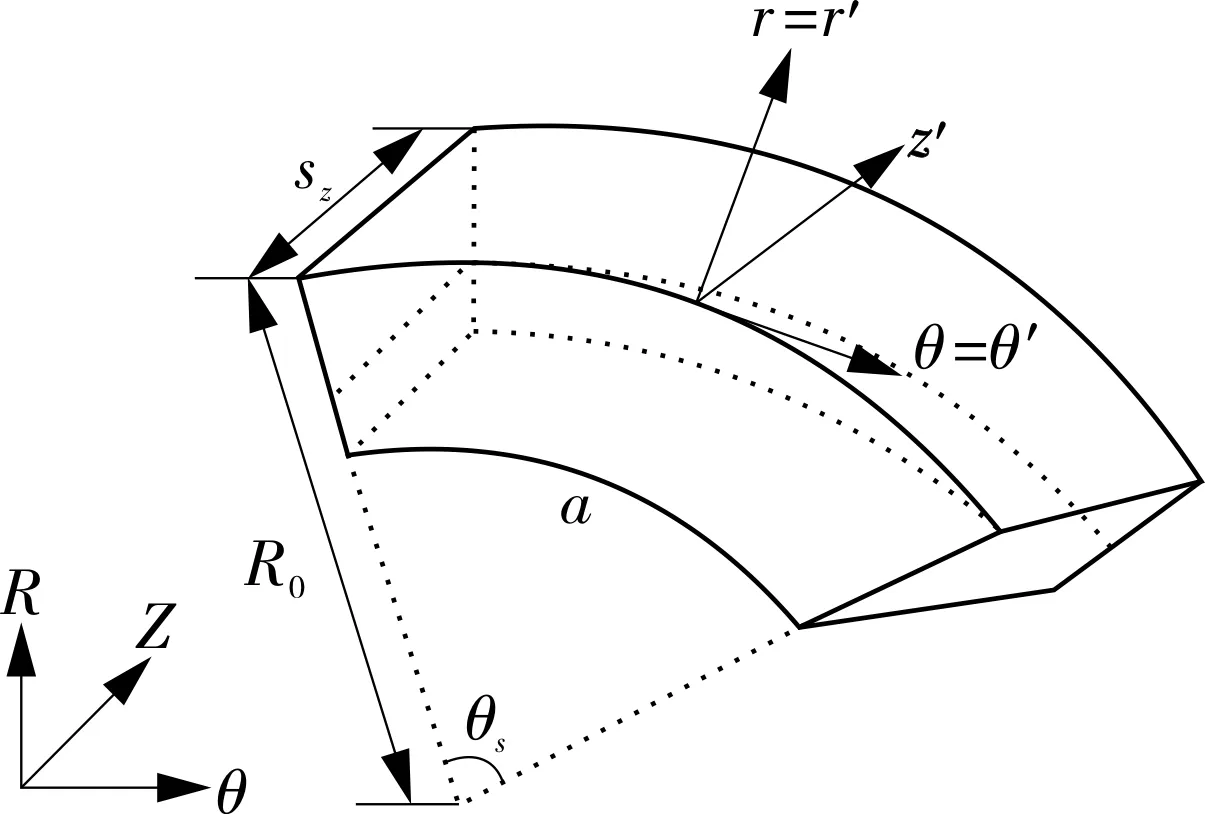
图3 元胞结构示意Fig.3 Schematic diagram of cell structure

1.2 等效的COMSOL模型

采用COMSOL MULTIPHYSIC有限元仿真软件中的固体力学模块，考虑R方向厚度为d的管道结构，基于上述理论建立如图4所示的元胞结构(以8层管道为例)。在Z方向上加Floquet周期性边界条件，在T方向上加连续性边界条件，厚度方向上使用自由边界条件。

图4中z是源边界和目标边界的距离，即Floquet 周期性边界条件中的晶格平移量，是由Z方向的本征波矢kz和边界的相对距离来确定的。需要注意的是，引入Floquet周期性边界条件会使得频散曲线在布洛赫边界发生折叠，对于管道结构来说这个折叠是虚假的。考虑到布里渊边界处波矢量的最大取值为π/z，可以使用较小的z值，将求解的特征频率折叠推到极高频，然后截断，即可得到所需的频散关系。使用较小的z值还可以简化模型的复杂性，从而减少计算时间。根据经验可知，z的取值为管道厚度d的1/10。θs为所取元胞结构的弧度，取值也相对小一点，可以减少网格的数量，从而减少计算时间。

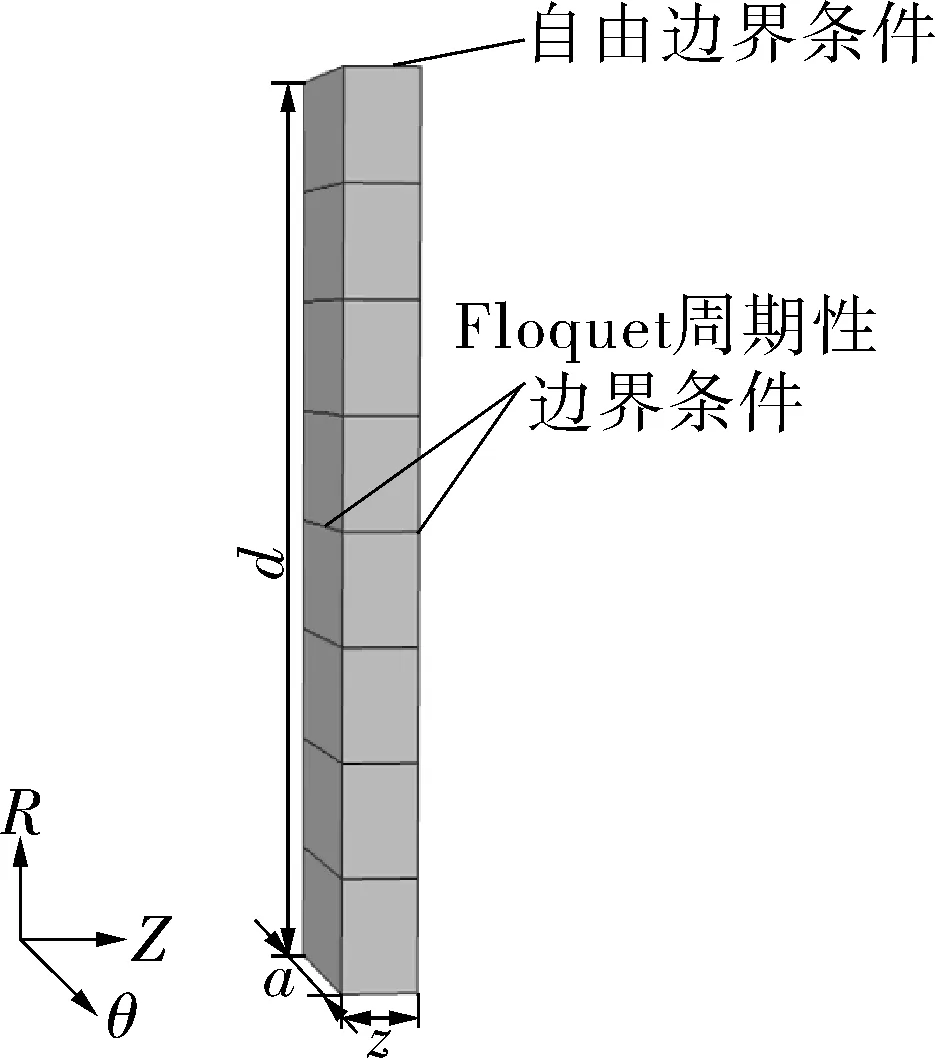
图4 8层管道元胞结构Fig.4 Cell structure of an eight-layer pipeline

同时，在利用有限元方法进行求解的过程中，由于周期性条件的引入会导致计算收敛性变差。为了提高收敛性，在进行网格划分时，需要注意使互为周期性的两个边界上的网格完全一致。通过波矢kz进行参数化扫描，可以求解出质点振动的本征方程对应于不同波矢的特征频率，进而求解多层复合管道的频散曲线。

2 复合材料管道中的频散特性

以图4的8层管道为例，管道内径为60 mm，长度为500 mm，采用上述方法对其频散特性进行分析。表1列出了单层材料属性，结构铺层顺序为[0/45/-45/90]s,每层厚度为0.15 mm。在COMSOL中建立相应的模型，元胞高度为管道原厚度，设置为1.2 mm，源边界与目标边界的距离z设置为0.12 mm，θs为0.3°。网格为自由四面体网格，网格尺寸采用预定义里的coarser(粗糙的)。得到的频散曲线见图5。

表1 材料参数Tab.1 Material parameters

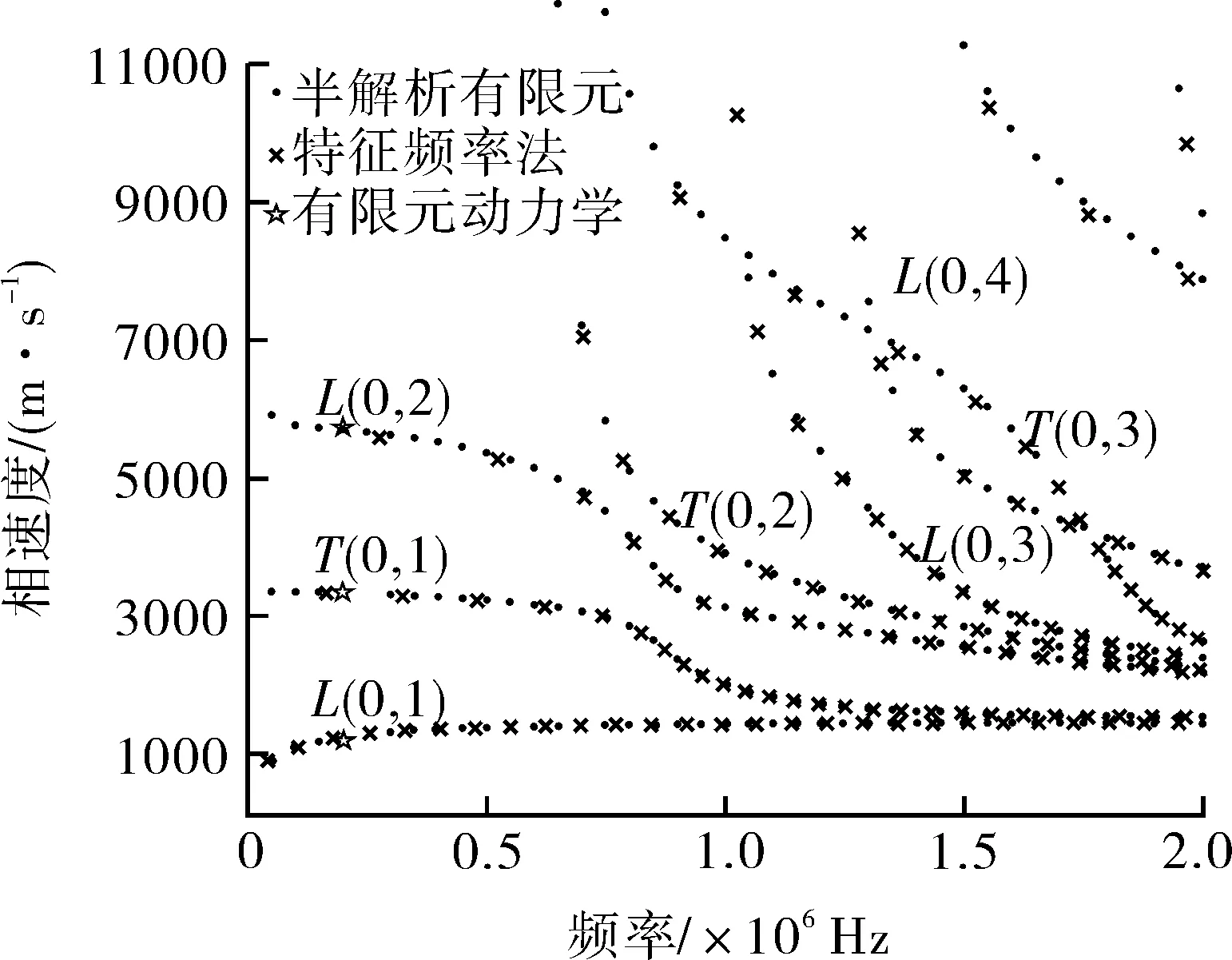
图5 [0/45/-45/90]s复合材料管道中的频散曲线

进一步对模态的波结构进行分析。取如下3个模态：k1=942.48 m-1，f1=181 kHz；k2=314.16 m-1，f2=166 kHz；k3=314.16 m-1，f3=279 kHz，在COMSOL中提取对应的特征向量，绘制波结构如图6所示。可以看出，图6(a)是以ur为主导，判断其为L(0,1)的波结构；图6(b)是以uθ为主导，判断其为T(0,1)的波结构；图6(c)是以uz为主导，判断其为L(0,2)的波结构。

使用半解析有限元法[24]对上述方法求解得到的频散曲线进行验证。选用一维二次单元在厚度方向进行有限元离散，每层厚度取2个单元，可以分析多层复合管道中导波的频散特性。图5初步验证了本文提出的特征频率方法求解频散曲线的正确性。

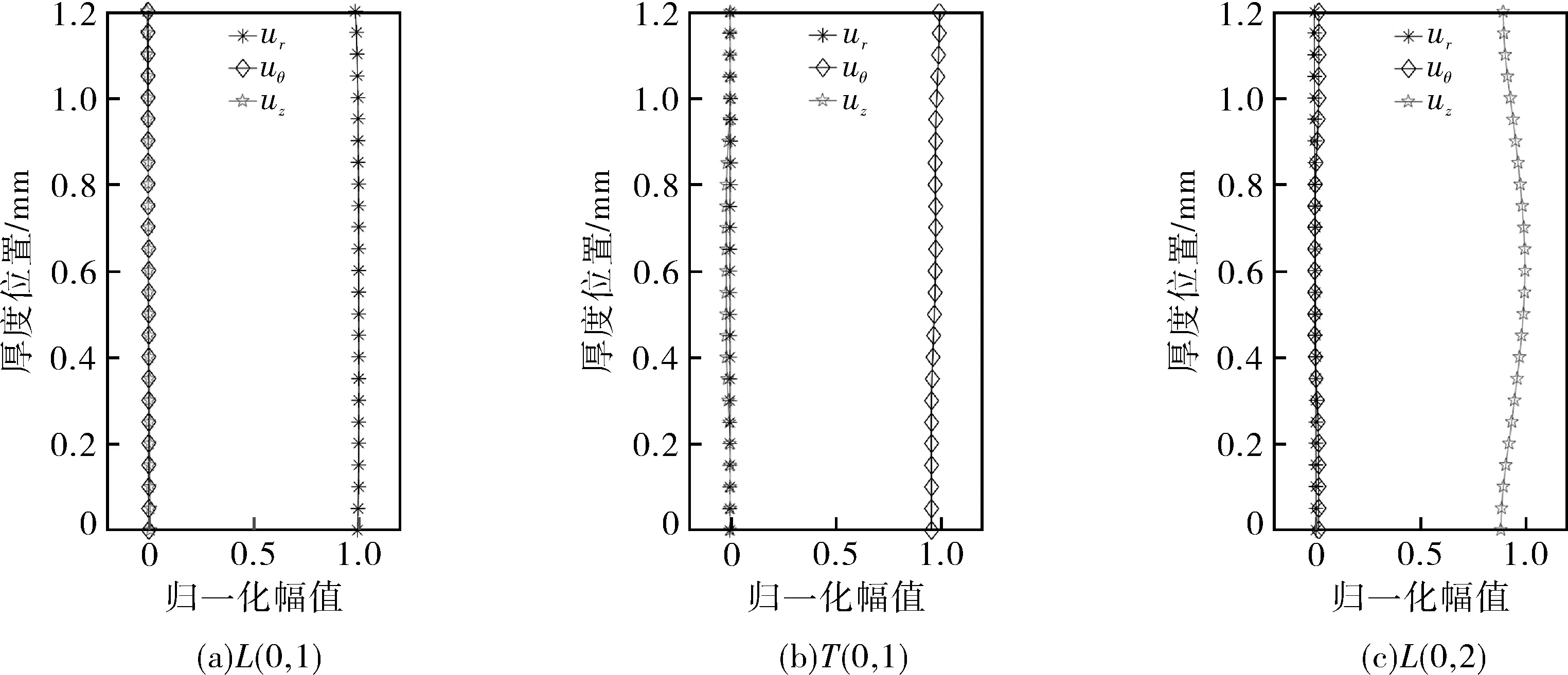
图6 波结构示意

采用Abaqus动力学分析模块，对200 kHz下的T(0,1)，L(0,1)，L(0,2)模态进行模拟，提取其传播速度，与上述方法作比较。

在Abaqus中建立对应的三维管道，长度为0.5 m，单元尺寸为1 mm，单元类型为C3D8R。采用隐式动力学分析步，设置固定增量步为2.5×10-7s。在管道的一端施加固定约束，另一端施加压力载荷，大小为五波峰调制的正弦信号:

(11)

式中，N为周期数，N=5；f0为中心频率，kHz，f0=200 kHz。

依据上述波结构分析结果，分别用3个方向上的力来加载，激励出L(0,1),L(0,2),T(0,1)模态，不同模态传播的云图如图7所示。

图7 不同模态传播的位移云图

管道轴向一条路径上所有节点的位移时域信号，通过一维傅里叶变换，将信号从时域转换至波数域，结果见图8。计算可得到相应的相速度。由表2可以看出，L(0,2),T(0,1)模态的COMSOL解(基于Floquet边界条件的有限元特征频率法)和Abaqus解(动力学方法)相差很小，但L(0,1)模态的相对误差较大。究其原因，L(0,1)模态的波长约为6 mm，仿真中单元尺寸设为1 mm，不满足一个波长内至少8～10个单元的要求，可能是导波L(0,1)模态的速度误差较大的原因。

图8 不同模态的位移空间信号与波数域信号

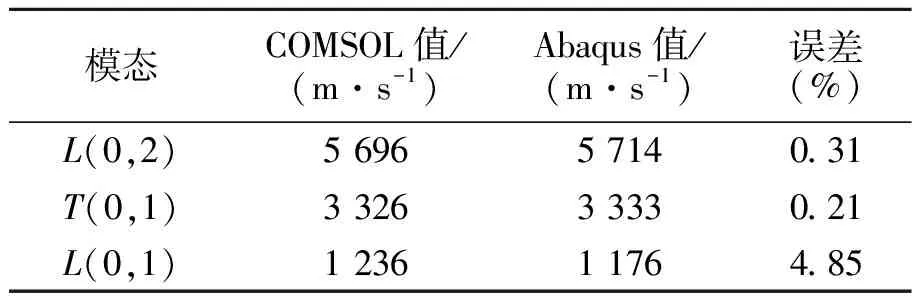
表2 COMSOL求解值与Abaqus求解值对比Tab.2 Comparison of COMSOL solved values withAbaqus solved values

注：COMSOL解为基于Floquet边界条件的有限元特征频率法;Abaqus解为动力学方法。

观察图5，基于3种方法求解的导波频散特性吻合度很高，验证了本文提出的有限元特征频率求解法求解频散曲线的正确性，同时也验证了本文建立的Abaqus模型的正确性。

3 分层损伤对导波传播特性的影响

3.1 损伤模型的建立

为了进一步研究分层损伤对导波传播特性的调制规律，在图7模型的基础上建立分层损伤。分层损伤通常认为是零体积的，且无法传递面内剪力。有限元软件中具体的设置方法是将有损伤的地方解除tie约束。

采用激励频率200 kHz下L(0,2)模态检测损伤，以图9为例，损伤大小为2 mm×2 mm，距离左端部250 mm处，位于第4层和第5层中间位置。传播的云图见图9，观察到经过损伤后有4股波出现，从左到右依次为经损伤反射的L(0,2)R、经损伤模态转换反射的L(0,1)R、经损伤模态转换透射的L(0,1)T以及经损伤透射的L(0,2)T。

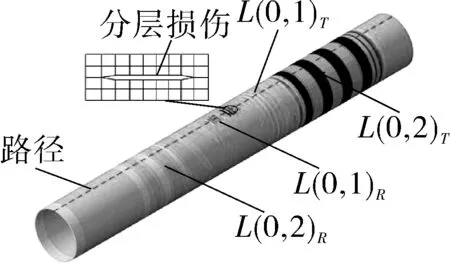
图9 含损伤管道反射波、透射波云图Fig.9 Nephograms of reflected and transmitted wavesin a pipe with delamination damage

(a)空间域

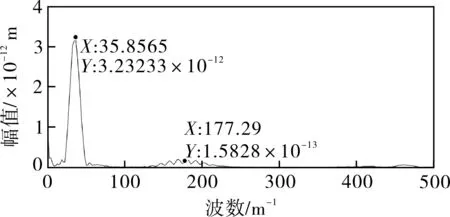
(b)波数域图10 含损伤多层复合材料管道结构中的导波信号Fig.10 Wave guided signals in a multilayer composite pipewith delamination damage

选取管道上的一条路径(如图9所示)，提取t=83.75 μs时刻下的空间域信号(见图10(a))，作一维傅里叶变换(见图10(b))。

由图10(b)可以看出两个波数峰值：k1=36 m-1，k2=177 m-1，分别对应模态为L(0,2)和L(0,1)，因此，可判断发生了从L(0,2)向L(0,1)的模态转换现象。

3.2 损伤深度对导波传播特性的影响

固定复合管道长度为500 mm，损伤尺寸为20 mm×20 mm，损伤发生在距离管道端部250 mm 处，通过改变分层发生的界面位置，分析其对导波传播特性的影响规律。不同损伤位置位移的空间域信号如图11所示。

图11 不同损伤深度的导波空间域信号Fig.11 Spatial domain signals of guided waves withdelamination damage in different depths

定义4种归一化的损伤因子IL(0,2)T，IL(0,1)T，IL(0,1)R，IL(0,2)R：

(12)

(13)

(14)

(15)

式中，IL(0,2)T，IL(0,1)T，IL(0,1)R，IL(0,2)R分别为L(0,2)模态透射因子、L(0,1)模态透射因子、L(0,1)模态反射因子以及L(0,2)模态反射因子；AL(0,2)T，AL(0,1)T，AL(0,1)R，AL(0,2)R分别为L(0,2)模态透射波幅值最大值、L(0,1)模态透射波幅值最大值、L(0,1)模态反射波幅值最大值以及L(0,2)模态反射波幅值最大值；A0为入射波幅值最大值。

从图12可以观察到，L(0,2)T随损伤深度变换呈波动变化，L(0,2)R和发生模态转换的L(0,1)T都随深度增大,呈现先减小、后增大的趋势，且都是损伤在第4层和第5层之间时达到最小值。随深度增大，L(0,1)R呈现先增大、后减小的趋势。

图12 不同损伤位置下的透射、反射、模态转换因子Fig.12 Transmission,reflection and mode conversionindicators with delamination damage in different depths

从图12还可以看出，发生模态转换得到的L(0,1)T的透射因子明显大于L(0,2)R的反射因子，因此相对于L(0,2)R，经由模态转换得到的L(0,1)T对分层损伤检测灵敏度更高。从以上的分析可以得出结论，L(0,1)T对损伤的敏感度明显高于L(0,2)R，并呈现一定的规律，这也为后续开展定位损伤检测提供基础。

3.3 损伤尺寸对导波传播特性的影响

固定损伤位置在第4层和第5层之间，固定轴向尺寸为20 mm，改变损伤的周向尺寸l，分析其对导波传播特性的影响规律。

由图13可以观察到，L(0,2)T随损伤尺寸的改变呈现波动变换；L(0,2)R反射因子一开始随着尺寸的变大而变大，当尺寸与波长的比值接近0.4时，反射因子达到最大，随着损伤尺寸的进一步变大，L(0,2)R的反射因子随损伤尺寸的变大而呈平缓上升的趋势；L(0,1)R反射因子一开始随尺寸的增大而逐渐减小，在损伤尺寸与波长的比值接近0.4时，L(0,1)R反射因子达到最小，随着尺寸的进一步增大，L(0,1)R反射因子随损伤尺寸的变大呈平缓上升的趋势；L(0,1)T透射因子一开始随尺寸的增大而逐渐减小，在损伤尺寸与波长的比值接近0.4时，L(0,1)R反射因子达到最小，随着尺寸的进一步增大，L(0,1)R反射因子随损伤尺寸的变大呈平缓上升的趋势。

图13 不同损伤尺寸下的透射、反射、模态转换因子Fig.13 Transmission,reflection and mode conversionindicators with delamination damage of different sizes

从图13还可以看出，损伤尺寸与波长之比小于0.5时，L(0,2)R反射因子显然大于经模态转换得到的L(0,1)的透射因子与反射因子，相对于L(0,1)T和L(0,1)R，L(0,2)R对分层损伤检测灵敏度更高，故此时适宜使用L(0,2)R进行损伤检测。但在损伤尺寸与波长之比介于0.5与1.6之间时，经模态转换的L(0,1)R的反射因子显然大于其透射因子与L(0,2)R的反射因子，此时则应使用经模态转换得到的L(0,1)R进行缺陷检测，这也为后续开展定量损伤检测提供了依据。

4 结论

本文基于Floquet周期性边界条件的有限元特征频率法，高效、简便地分析了多层复合材料管道中的超声导波频散特性；并建立了含分层损伤的复合材料管道中的超声导波动力学模型，针对反射和模态转换两种因子，研究了损伤深度和尺寸对导波传播特性的影响，得出以下结论。

(1)基于有限元特征频率法，引入Floquet周期性边界条件，将复合材料管道中的超声波传播的频散控制方程转化为元胞结构的特征频率方程，高效地分析了导波频散特性。该方法不需要编程，且对不同波导结构具有普适性。

(2)在分层损伤处会发生L(0,2)到L(0,1)的模态转换。当损伤发生在不同深度时，经损伤发生模态转换的L(0,1)T对损伤的敏感度最大。损伤尺寸与波长比值小于0.5时，L(0,2)R对损伤的敏感度最大；当损伤尺寸与波长比值大于0.5时，经损伤发生模态转换的L(0,1)R对损伤的敏感度最大。

(3)多损伤因子分析可为分层损伤的定量检测提供依据。