微柱压缩试验：在役设备强度的微损测试法

章骁程，徐 彤，关凯书

(1.华东理工大学,上海 200237;2.中国特种设备检测研究院，北京 100013)

0 引言

在火电、核电、冶金、炼化、化工、航空、航天等行业中，存在着大量压力容器和管道，它们长期服役于高温、高压、强腐蚀、中子辐照等环境中[1-3]。这些设备经历数十年的服役后，材料面临着力学性能退化的风险(如：强度降低导致结构的承载能力下降；韧性降低导致结构对缺陷的敏感性增加，易发生脆断等)。还有一些设备由于事故或失误，导致操作参数短时间超出设计值，也面临着安全风险。如果这些设备失效，易燃、有毒的介质泄漏到环境中，会产生灾难性的后果。能够对这些设备进行适用性评估(Fitness-For-Service)，在确保安全的前提下尽可能地延长其使用寿命，将产生巨大的经济和社会效益。准确地获得这些设备的材料力学性能是适用性评估的重要前提。

目前应用比较广泛的在役设备力学性能测试方法主要有仪器化压痕法[4]和小冲杆测试法[5]。压痕法从硬度试验发展而来，可以获得材料的压痕硬度、弹性模量、强度、残余应力等力学性能[6-10]，对被测表面进行适当的打磨便可进行测试，效率较高，适合批量快速测试，但也存在一些不足，比如测试结果依赖预设的本构方程、易受残余应力干扰、压入深度浅对环境扰动敏感等；小冲杆测试法，最早用于评价辐照脆化材料，能够测试材料的屈服强度、抗拉强度、断裂韧度、蠕变性能、韧脆转变温度等参数[11-18]，小冲杆试验的所有步骤均在实验室中完成，试样经历弹性变形、塑性变形和断裂的完整过程，获得信息全面、测试精度高，但是取样和制样过程相对繁琐，测试效率较低。

本文针对现有测试方法中存在的一些不足，提出一种新的测试方法——微柱压缩试验(Macro Pillar Compression Testing，MPCT)，在设备表面制备试样并完成测试。与小冲杆试验相比，免去了取样步骤，提高了测试效率；与压痕法相比，测试不受残余应力影响、压入深度大，抗环境干扰能力强、不需要预设本构方程即可获得真应力-应变曲线。

微柱压缩试验的基本原理如图1所示。采用机械加工方法移除被测表面的部分材料，制备一个小型圆柱形试样，称之为微柱(见图1(a))；然后使用平底压头压缩微柱的顶部(见图1(b))，获得压缩载荷-位移曲线，并据此计算材料的屈服强度和抗拉强度。配合现场测试仪，可以在设备表面进行微柱压缩试验(见图2)。微柱压缩试验是一种全新的测试方法，没有先例可循，本文主要对加工方法、测试理论等方面进行研究和论述。

(a)加工试样

(b)测试过程图1 微柱压缩试验原理图Fig.1 Schematic diagram of MPCT

图2 现场试验示意Fig.2 Schematic diagram of site testing

1 试样加工

图3(a)示出设计的电火花加工设备，其具有轻便、高精度、高效率的优点；加工原理如图3(b)所示；电极采用钨铜合金材料，设计成中空管状结构，如图3(c)所示。工作液由电极内部注入后，从电极和试样的间隙流出。伺服系统控制加工深度(试样高度)，试样直径则由电极内径决定。

(a)实物

(b)原理图

(c)钨铜合金电极图3 便携式电火花微柱试样加工设备Fig.3 Portable spark machining equipment for micropillar specimen

加工完成的试样如图4(a)所示，在同一基体上加工多个微柱试样，可以提高材料利用率和测试效率。相邻微柱的间距建议大于3倍直径，避免应变场相互干扰。将试样沿中心线对半剖开，置于金相显微镜下测量尺寸，如图4(b)所示，微柱试样的高度为2 mm，直径为1.5 mm，与设计的尺寸一致。需要注意的是，试样根部存在一个半径0.12 mm的圆弧，这是由于电极自身烧蚀所产生，在固定加工参数和每次均采用全新电极以后，此圆弧可视为定值。

2 获得材料强度的半解析法

试样受轴向压缩时，一般只发生鼓胀，不发生断裂，故只能直接测得材料的屈服强度，不能得到抗拉强度。抗拉强度可以通过有限元模拟单轴拉伸试验间接获得，但是必须知道材料的真应力-应变曲线。微柱压缩鼓胀是一个高度非线性问题，无精确的析解，本节提出了一种计算真应力-应变曲线的半解析方法，即以解析推导为主，其中若干参数采用有限元模拟标定的方法。

(a)试样照片

(b)试样尺寸图4 微柱压缩试验的试样Fig.4 Specimens for MPCT testing

半解析法的技术路线如图5所示，主要分为4步：制样和测试、沉陷修正、鼓胀修正、求解强度。其中鼓胀修正涉及2个形状修正系数，需要用有限元方法标定。

图5 用微柱压缩试验获得材料强度的流程图Fig.5 Flow chart for obtaining strengths of materialsusing MPCT

2.1 沉陷修正

压缩时基体会下凹变形，发生沉陷效应，导致传感器测得的微柱高度小于实际高度。微柱沉陷的几何模型如图6所示，由于结构限制，位移传感器只能测量压头顶端的位移变化量ΔH，必须从中扣除沉陷深度Hsink，才能得到微柱高度Hp。

图6 沉陷效应的几何模型Fig.6 Geometric model for sinking effect

根据SNEDDON[19]的刚体圆柱压头压入弹性半空间模型，将微柱视为的刚体圆柱型压头，基体当作弹性半空间，那么微柱试样的沉陷深度Hsink可以用式(1)和式(2)来定义，并导出微柱高度Hp的表达式(3)。

Hsink=CSneddonF

(1)

(2)

Hp=Hp0-ΔH+CSneddonF

(3)

式中,CSneddon为弹性半空间的变形协调系数；F为施加在微柱顶端的载荷；υ为柏松比；E为杨氏弹性模量；Ap微柱底端与基体的接触面积，由于两者相连，接触面积等于微柱底部的截面面积；Hp为微柱试样的高度。

2.2 鼓胀修正

(4)

(5)

(6)

图7 AVITZUR鼓胀效应的速度场模型Fig.7 Velocity filed model for barreling effect providedby AVITZUR

图8 微柱压缩试样变形的比较Fig.8 Comparison of deformed shapes of micro pillarcompression test specimens

微柱压缩鼓胀与AVITZUR模型不完全一致。因为微柱顶端是一般滑动摩擦状态，而微柱的底端与基体连接在一起，上下部分的变形不对称，如图8所示。为此在AVITZUR的虚拟有效半径算式中引入了2个形状修正系数β和γ，如式(7)所示。

(7)

式中，R0，H0为微柱试样的初始半径和初始高度；H为试验过程中微柱试样的高度；β，γ是鼓胀效应的形状修正系数，需要采用有限元的方法进行标定。

KHODDAM等[20]对AVITZUR的轴向应变分量算式进行了简化，使其便于积分运算，如式(8)和式(9)所示。

(8)

α1=8HH0e-2bz/(H0+H)+H(H0+H)e-bz/H0

+H0(H0+H)e-bz/H

(9)

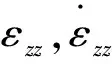
本文将微柱试样的等效真应变等价为沿z轴方向的平均应变，故对式(8)进行0～0.5H范围的积分运算，得到微柱上半部分沿z轴方向的变形量，再将总变形量除以上半部分的高度0.5H，得到式(10)。微柱试样的真应力等于载荷除以虚拟有效截面积，如式(11)所示。

(10)

(11)

式中,εtrue(MPCT)为微柱试样的等效真应变；H为微柱在试验过程中的高，mm；α1，b为中间变量；R0，H0为微柱试样的初始半径和初始高度，mm；σtrue(MPCT )为微柱试样的真应力，MPa；F为施加在微柱上的载荷，N；β，γ为鼓胀效应的形状修正系数。

2.3 形状修正系数的标定

本文认为形状修正系数是几何尺寸相关的参数，与力学性能无关。也就是说，对于特定尺寸的微柱试样(如文中微柱的直径1.5 mm、高度2 mm)，用有限元软件标定得到一组形状修正系数，就可以适用于所有的材料。

图9的标定流程主要分为两步：第一步用假设的真应力-应变曲线和有限元模拟来构造压缩载荷-位移曲线；第二步是参数标定过程，先假设一组β，γ，用式(10)(11)从第一步的压缩载荷-位移曲线中计算得到真应力-应变曲线，并作为式(12)中的曲线B。将第一步假设的真应力-应变曲线作为目标曲线A，用目标函数式(12)计算曲线A和B的差异。如果曲线之间的差异大于5%时，那么调整β，γ后再次进行第二步，如此反复直到两条曲线的差异小于5%为止。

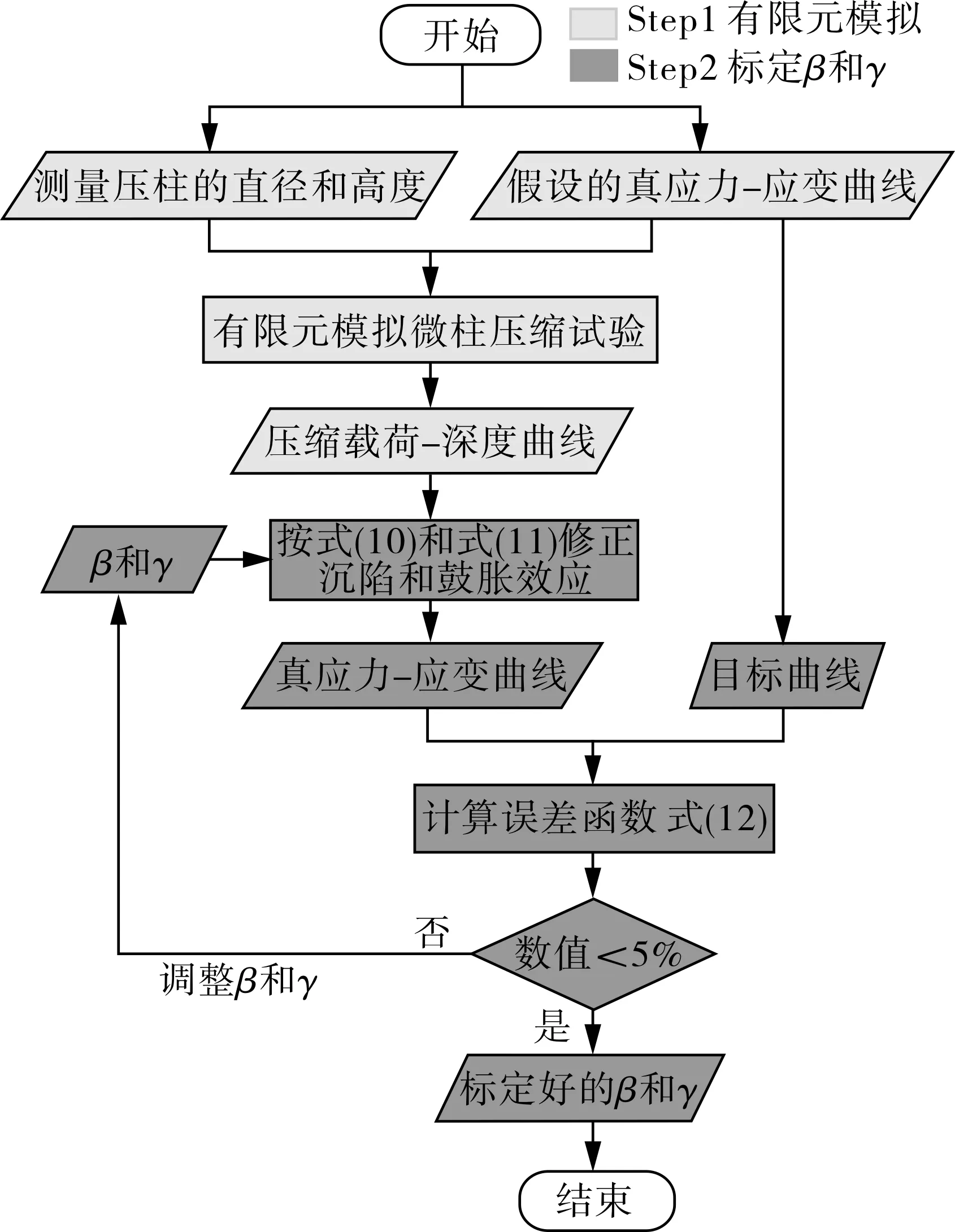
图9 标定形状修正系数的流程图Fig.9 Flow chart of correction factor for shape calibration

(12)

式中,F(x)为目标函数；n为离散点的最大数量；σ(εi)A,σ(εi)B为两条真应力-应变曲线，如图10所示。

图10 用于量化两条真应力-应变曲线差异的目标函数Fig.10 Objective function used to quantify the differencebetween two true stress-strain curves

微柱压缩的二维轴对称有限元模型如图11所示，为避免应力集中的影响，基体高度取6.5 mm，半径取5.5 mm。压头采用解析刚体建模，压头和微柱顶端的摩擦系数取0.13。基体底面除x方向以外的所有自由度均被约束。

图11 微柱压缩试验的有限元模型Fig.11 FEM model for MPCT

标定流程使用6种假设材料，包括低碳钢(低屈强比、长屈服平台)、低合金钢(高屈强比、幂硬化)和奥氏体不锈钢(线性硬化)，如图12所示。杨氏模量和泊松比均为200 GPa和0.3。使用图11的有限元模型，模拟得到6条对应的压缩载荷-位移曲线，如图13所示。

图12 6种假设的材料用于标定形状修正系数Fig.12 6 hypothetical materials for calibration ofcorrection factors

形状修正系数β的取值范围设定为1～1.1，γ的取值范围为-0.1～0。使用Matlab软件编写的脚本自动调整形状修正系数，最终得到的β和γ分别为1.04和-0.08，误差如表1所示，计算的和假设的真应力-应变曲线如图14所示。

图13 6种假设材料的压缩载荷-位移曲线Fig.13 Compression load-displacement curves for6 hypothetical materials

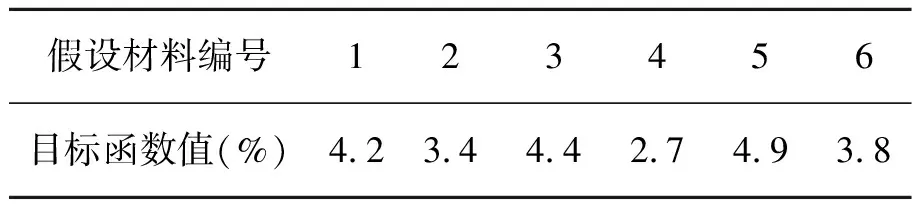
表1 6种假设材料的目标函数值(β= 1.04，γ=-0.08)Tab.1 Values of objective function for 6 hypothetical materials(β=1.04，γ=-0.08)

图14 计算的和假设的真应力-应变曲线

3 试验验证

试验验证准备了3种不同类型的结构钢(23CrMoNiWV88，A508 Gr.3和SA182 F316L)，化学成分如表2所示。每一种材料都制备了3个单轴拉伸试样和3个微柱试样，并取自同一块金属材料，如图15所示。单轴拉伸试样的直径为5 mm，标距长度为25 mm。微柱压缩试样的直径为1.5 mm，高度为2 mm。

表2 验证所用的3种钢的化学成分Tab.2 Chemical composition of 3 steels for verification %

(a)取样示意

(b)取样照片图15 单轴拉伸和微柱压缩试验取样Fig.15 Sampling method of tensile testing and MPCT

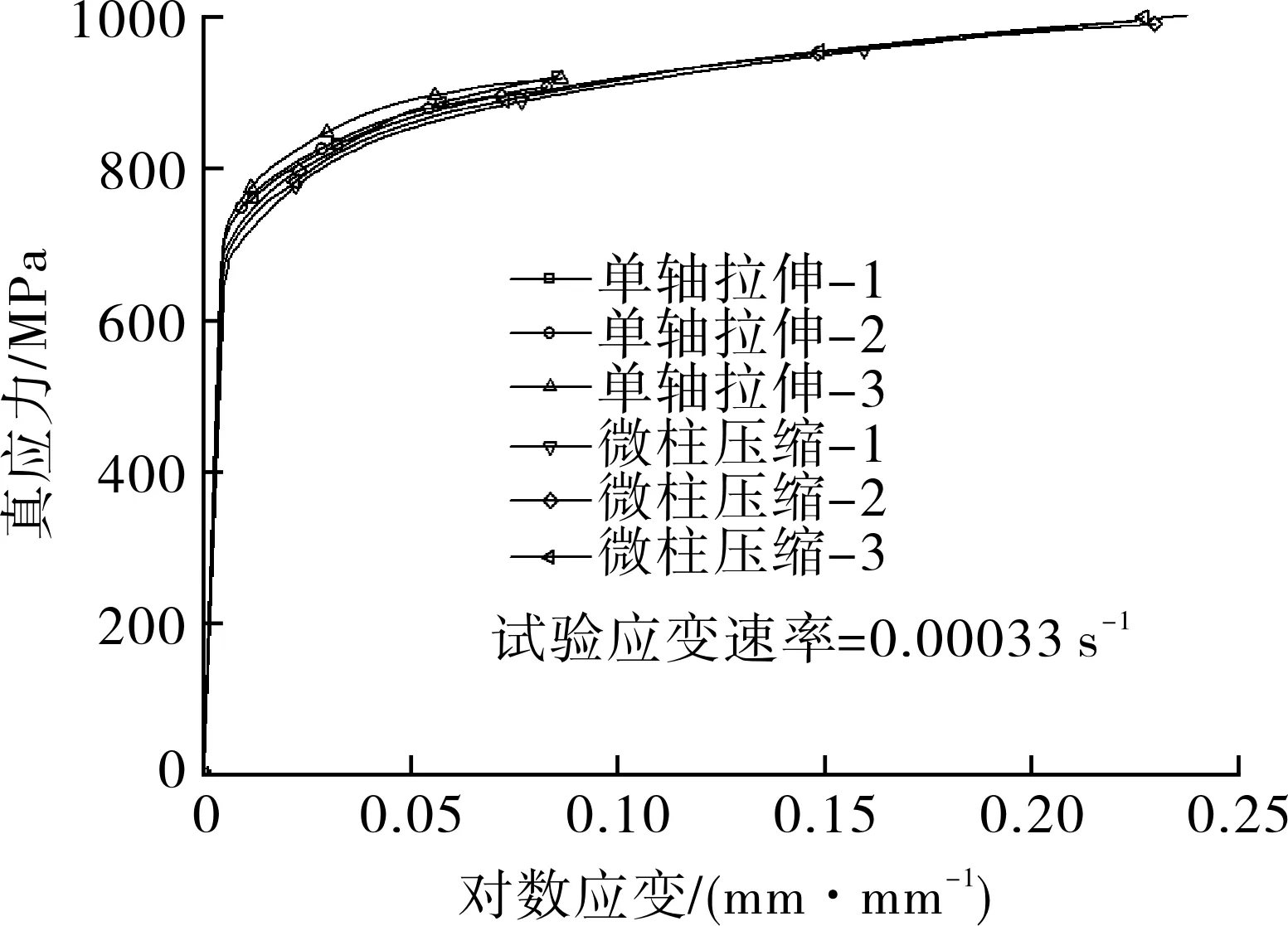
(a)23CrMoNiWV858钢

(b)A508钢

(c) F316L钢图16 单轴拉伸和微柱压缩获得的真应力-应变曲线Fig.16 True stress-strain curves obtained by tensiletesting and MPCT

测试选用的准静态加载速率为0.000 33 s-1，根据试样的高度将应变速率换算成试验机的横梁移动速度，单轴拉伸试验为0.5 mm/min，微柱压缩试验为0.04 mm/min。试验温度为25 ℃，测试得到的真应力-应变曲线如图16所示。

单轴拉伸试验的二维轴对称有限元模型如图17所示，试样直径为5 mm、标距段长度为25 mm，用刚性梁单元在试样大端建立一个控制节点，位移载荷施加到该节点上。

将微柱压缩试验得到的真应力-应变曲线输入上述有限元模型，模拟得到工程应力-应变曲线，并用作图法得到材料的屈服强度和抗拉强度，如表3,4所示。可以看出，材料屈服强度的最大误差为8.1%，抗拉强度的最大误差为8.0%。

表3 单轴拉伸和微柱压缩测得的屈服强度Tab.3 Yield strengths obtained by tensile testing and MPCT

表4 单轴拉伸和微柱压缩测得的抗拉强度Tab.4 Tensile strengths obtained by tensile testing and MPCT

图17 单轴拉伸试验的有限元模型

4 结论

本文针对现有微损测试方法中存在的一些不足，提出了现场制备试样、现场完成测试的理念，并据此设计了一种新的测试方法——微柱压缩试验。给出了计算真应力-应变曲线的半解析法，用形状修正系数解决了不对称压缩鼓胀无解析解的问题。经过3种真实材料的实际验证，微柱压缩试验获得的强度与单轴拉伸试验结果具有较好的一致性，具有较好的使用前景。