关于ASME Ⅷ-2附录5-E多孔板等效方法的讨论
万里平,朱国栋
(1.中国石化工程建设有限公司,北京 100101;2.中国特种设备检测研究院,北京 100029)
符号说明:
E——多孔板在设计温度下的弹性模量,MPa;
E*——三角形布管的管板等效为当量圆平板后的等效弹性模量,MPa;

Ez*——三角形布管的管板等效为当量圆平板后的厚度方向等效弹性模量,MPa;
υ——多孔板的材料泊松比;
υ*——三角形布管的管板等效为当量圆平板后的等效泊松比;
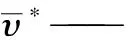
η——抗弯刚度系数;
μ*——管带系数,同ASME规范;
h——管板厚度,mm;
p——管心距,mm;
d*——有效管孔直径,同ASME规范,mm;
G——多孔板剪切模量,MPa;
G*——三角形布管的管板等效为当量圆平板后的等效剪切模量,MPa;

Gz*——三角形布管的管板等效为当量圆平板后承受横向剪切载荷的等效剪切模量,MPa;
KPS——确定管板表面膜加弯应力的放大系数
0 引言
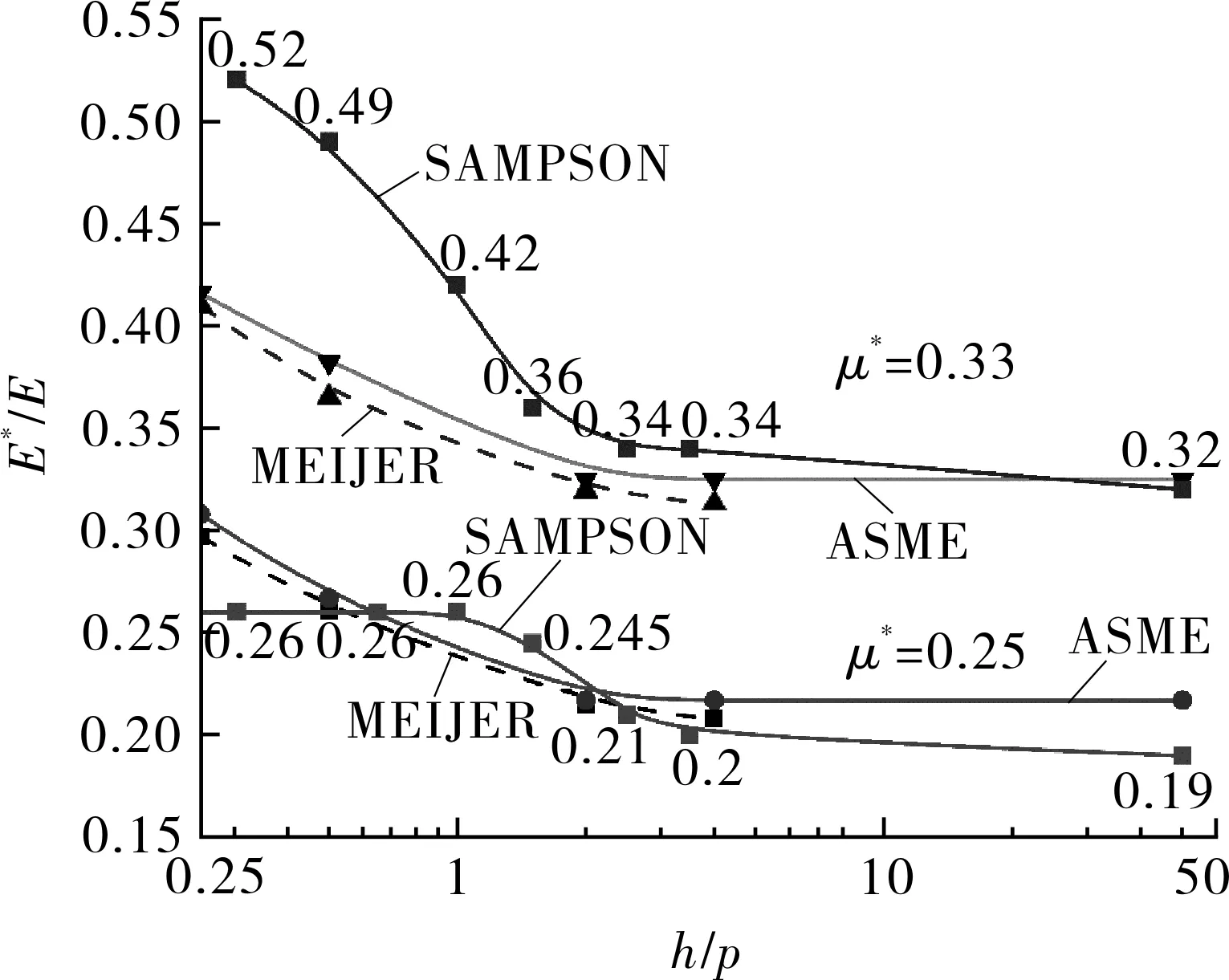
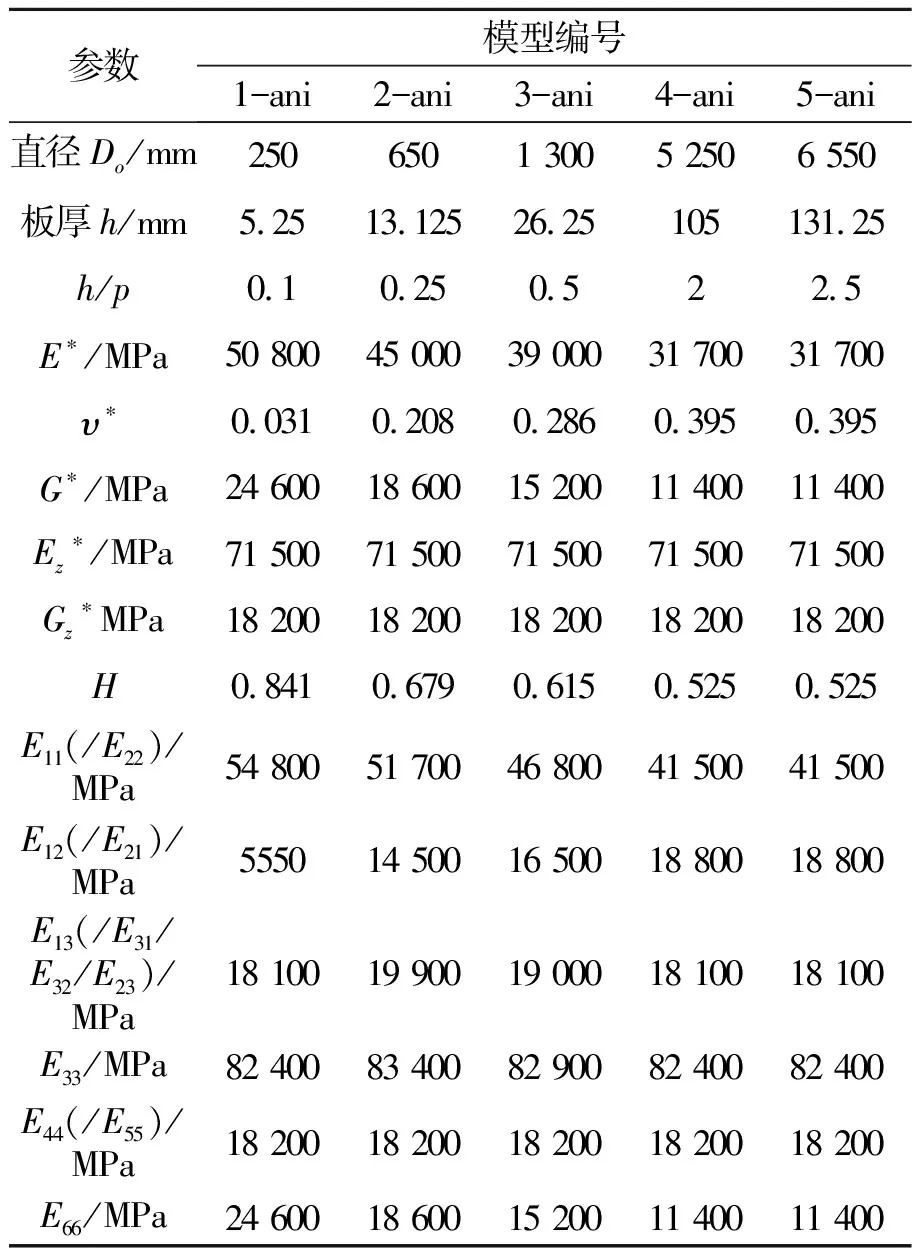
换热器是石化装置中最常见的热交换设备,随着装置大型化,换热器的规模也逐渐增大,对于某些超过常规设计规范的换热器,需要按照分析设计规范,采用有限元方法进行数值模拟及应力评定[1-3]。换热器的数值模拟中,核心内容在于管板和换热管的模拟。采用分析设计的换热器通常直径较大,布管数量较多,若按照实际结构建立真实管板和换热管模型,则模型单元网格数量较大,计算效率较低。世界几大压力容器设计体系中,均采用了将开孔的管板等效为开孔削弱当量圆平板的计算方法,对当量圆平板计算等效弹性模量E*和等效泊松比υ*,使得等效圆平板与原开孔管板具有相同的刚度和强度。
合理确定等效削弱参数保证了等效圆平板变形和应力结果的准确性。OSWEILLER[4]对1948年至1989年期间发表的关于等效削弱参数的61篇研究文献进行了综述,介绍了等效削弱参数的理论、试验基础和标准采信情况。2014年ASME PTB-7—2014 ASME Ⅷ-1 UHX篇《管壳式换热器标准释义》进一步介绍了等效削弱参数的3个研究阶段和ASME采信情况。结合文献[4]与ASME PTB-7—2014,可以看到:(1)1948年至1959年,针对三角形布管方式,引入抗弯刚度系数η用以描述开孔对平板变形的影响,发现等效弹性模量E*和等效泊松比υ*与以下因素有关,即管带系数,板厚,原材料弹性模量和泊松比,以及载荷形式(面内载荷或弯曲载荷),通过试验确定了管带系数μ*=0.285的三角形布管管板,在全布满和非全布满等情况下的刚度减弱系数η,该系数1965年引入BS 1515—1965《焊接式压力容器》;(2)1960年至1962年,研究对象仍为三角形布管管板,以h/p=2作为薄管板和厚管板的分界线,对于h/p≥2的平板,载荷形式对于等效削弱参数影响非常小,此时E*/E和υ*可以表示为管带系数μ*的函数,1966年版的ASME Ⅲ和ASME Ⅷ-2采纳了这一研究成果;(3)1963年至1985年,得益于高性能计算机诞生以及有限元方法的快速发展,进一步研究了四边形布管管板的等效削弱参数,提出沿管心距方向和对角线方向的等效削弱参数不同,并通过试验及有限元方法给出了0.1 ASME Ⅷ-2(2021版)附录5-E多孔板的等效方案,总的思路如下:(1)通过Option A/B/C任一方案,得到等效弹性模量E*,Ez*,等效剪切模量G*,Gz*,以及等效泊松比υ*等参数;(2)计算各向异性等效弹性模量矩阵的E11~E66等参数;(3)有限元模型中,设置各向异性弹性模量,载荷边界条件根据实际情况进行调整;(4)评定时许用应力极限值需引入KPS和μ*作为系数。附录5-E中Option A和Option B均给出简化过程需要的等效削弱参数,Option C方案是通过数值模拟得出等效削弱参数。 近年来,随着炼化装置产能快速增长,换热器的直径不断增加,附录5-E在换热器的设计中得到越来越多的应用[12-14]。由于附录5-E中没有指明Option A和Option B的区别,工程人员在选择方案上可能存在疑问。本文对Option A和Option B两种多孔板简化方案进行探讨,并从力学理论角度分析A与B的区别,为工程人员进行管板简化提供参考,最后对各向异性和各向同性等效削弱参数对当量圆平板分析结果的影响进行对比研究。 附录5-E的适用范围为数量不小于19个开孔的正三角形或正方形均布且垂直开孔的圆形多孔板。前人研究表明,等效削弱参数与载荷形式(平面内载荷或弯曲载荷),h/p,管孔排布形式(正三角形或正四边形)及管带系数μ*等相关。Option A适用于所有厚度圆平板,不同的h/p对应不同的等效削弱参数,该方案对平面内载荷和弯曲载荷情况均适用。Option B的h/p分两种情况,当h/p<2时,采用平面应力的参数,且仅适用于平面内载荷;当h/p≥2时,采用一般平面应变的参数,考虑了平面内载荷和弯曲载荷情况。无论何种方案,对于h/p<0.1,按h/p=0.1取值;对于h/p>2,按h/p=2取值。两种方案的适用范围不同,使用方法不同,计算结果的差异性更关系到设计合理性和运行安全,下文以正三角形分布的管板为例,进行详细讨论。 Option A中,等效削弱参数E*和υ*是与h/p和μ*的函数。以正三角形布管的管板为例,E*和υ*与μ*的函数关系见式(1)(2),ASME Ⅷ-2表5-E.1和表5-E.2给出了此两项关系式系数A1~A7,B1~B7的值,取值与h/p相关。 (1) (2) h/p和μ*与以下几个管板实际几何参数有关:管板厚度h,管心距p,有效管孔直径d*。文献[4]认为,ASME Ⅷ-2使用的管板等效方法,结合了O′DONNELL和LANGER的理论,以及SAMPSON和MEIJER的试验数据。文献[4]给出了MEIJERS的试验值,见表1。为验证ASME规范中等效削弱参数的来源,通过式(1)(2),分别计算μ*=0.25和0.33时,不同的h/p对应的E*/E,列入表1。 表1 E*/E的MEIJERS试验值与ASME Ⅷ-2附录5-E的数据对比Tab.1 The comparison of E*/E between experimental data by MEIJERS and data as per Appendix 5-E,ASME Ⅷ-2 由表1的数据可以看出,Option A采用的等效削弱参数与MEIJERS试验值非常接近,可见该参数具有试验数据作为支撑。Option A中E*/E计算结果较试验值多数情况偏大。 图1 μ*=0.25,0.33时,E*/E随h/p变化的曲线Fig.1 The trend curves of E*/E with variable h/pwhen μ*=0.25,0.33 O′DONNELL[10]给出了SAMPSON的试验数据,图1示出SAMPSON和MEIJERS试验数据与ASME Option A计算值进行对比,可以看出,在h/p>2的范围内,试验数据和Option A计算值非常接近,当μ*=0.25时,Option A 取为定值,并大于SAMPSON的试验数据;当μ*=0.33时,Option A取值在两次试验值附近。 由表1和图1可以看出,在0.1 表2 ASME规范中Option A与ASME Ⅷ-2中4.18节的E*/E计算值对比Tab.2 The comparison of E*/E in Option A and Subsection 4.18 in ASME Ⅷ-2 Option B给出了计算等效弹性模量E*,Ez*,等效剪切模量G*,Gz*,以及等效泊松比υ*等参数的公式。对于不同的h/p,按两种情况处理:h/p<2时,视为平面应力状态,按式(3)~(5)计算,h/p≥2时,视为一般平面应变状态,按式(6)~(8)计算。平面应力和一般平面应变时其他面外等效参量的修正按式(9)(10)计算。 平面应力: E*=E[-0.000710796+0.138017μ*+4.22004μ*2 -7.55885μ*3+7.08667μ*4-2.88588μ*5] (3) υ*=0.999804-3.94540μ*+8.47377μ*2-8.02434μ*3 +2.79724μ*4 (4) (5) 一般平面应变: (6) (7) (8) 平面应力和一般平面应变: (9) Gz*=G(0.000209547+3.00960μ*+32.784μ*2 -16.57921μ*3)/(1+34.783μ*-33.7539μ*2 +17.1860μ*3) (10) 因此,对于μ*一定的管板,不同的h/p,计算得到的E*/E和υ*只有两组数值,仅在h/p=2时,E*/E和υ*开始发生变化。文献[11]中,对于h/p<2的平面应力状态,不再考虑h/p的影响,均按平面应力状态考虑,给出了E*/E和υ*与μ*的关系,文献[4]中的表2对文献[11]的数据进行了整理。下面采用Option B的公式,计算得到E*/E和υ*的值,与文献[4]中的相应数据共同列入表3。 表3 文献[11]与Option B的数据对比Tab.3 The comparison of data between reference [11]and Option B 由表3可看出,对于平面应力问题,Option B和SLOT-O′DONNELL给出的E*/E和υ*非常接近,因此可以判断,Option B与SLOT和O′DONNELL理论结果有很好的一致性。而一般平面应变问题,Option B同样采用了文献[10-11]中给出的E*/E和υ*与μ*的函数关系,同样符合SLOT-O′DONNELL理论。 经前文分析可知,Option A方案基于O′DONNELL和LANGER的理论成果及SAMPSON和MEIJER的试验数据,Option B方案基于O′DONNELL[11]的理论成果。 对于h/p<2,Option A根据MEIJERS的试验数据,给出E*/E和υ*关于h/p和μ*的计算公式,随h/p和μ*不同而不同,对于h/p>2,取h/p=2的数据,即E*/E和υ*仅与μ*相关,与h/p(主要体现为管板厚度h)无关;对于h/p<2,Option B认为管板处于平面应力状态,E*/E和υ*仅与μ*相关,与h/p无关,h/p≥2,Option B认为管板处于一般平面应变状态,也给出了E*/E和υ*关于μ*的计算公式,认为管板厚度对等效削弱参数影响不大。 文献[6]指出,当h/p>2,即对厚管板而言,承受面内载荷和弯曲载荷时,对等效削弱参数影响不大,而当h/p<2时,面内载荷与弯曲载荷对该参数有所影响。Option B同SLOT-O′DONNELL的理论,平面应力状态的理论公式推导基于面内载荷得出,因此,ASME Ⅷ-2中规定,Option B方案在h/p<2时,仅适用于承受面内载荷的情况,而Option A在h/p<2时的等效削弱参数基于MEIJERS的试验数据得出,因此Option A无载荷类型的限制。显然,对于换热器管板承受管程与壳程压力且h/p<2时,一般存在面内载荷和弯曲载荷,按Option B方案会出现偏差,建议采用Option A进行计算。 以下对Option A和Option B进行数据比较。表4示出了μ*=0.33时,Option A和Option B计算得到的E*/E和υ*与h/p之间的关系。可以看出,当h/p<2时,两者差别较大,Option A的E*/E随h/p增大而降低,Option B的E*/E保持不变;当h/p>2时,由于Option A和Option B规定按h/p=2处理,Option A和Option B计算得到E*/E和υ*相近。 表4 Option A和Option B的数据对比Tab.4 The comparison of data between Option A and Option B (11) (12) (13) 在此基础上,附录5-E引入等效剪切模量G*,圆平板z方向有关的Ez*和Gz*等参数,可更准确描述圆平板尤其是厚平板的实际应力状态。在文献[11]中,对一般平面应变状态的管板如何获得各向异性弹性矩阵的参数,给出了详细的推导。以三角形布管为例,文献[11]中式(58)~(75)给出了相应的力学关系,为便于理解,对其进行整理(见式(14)~(19)),将其以矩阵形式表示为式(20)。对比式(14)~(16)和式(11)~(13)可知,各向同性与各向异性弹性模量区别主要在于z方向有关的Ez*和Gz*等参数。 (14) (15) (16) (17) (18) (19) (20) 求式(20)中6×6矩阵的逆矩阵,即得到式(21)~(28)所示的,与ASME Ⅷ-2中表5-E.8相似的各向异性弹性模量矩阵。 (21) (22) (23) (24) (25) (26) (27) (28) (29) 图2 模型1-iso的网格模型和边界条件示意Fig.2 Schematic diagram of grid model and constraintboundaries of Model 1-iso 为进一步研究各向异性弹性模量矩阵对等效圆平板刚度和强度的影响,建立若干不同厚度h的等效圆平板有限元模型,采用Solid 185单元,平板厚度方向划分6层网格,原管板正三角形布管,管心距p=52.5 mm,管带系数μ*=0.25,管板材料的弹性模量E=1.46×105MPa,泊松比υ=0.3。在圆平板表面施加1 MPa的压力载荷,约束平板外侧面的节点在柱坐标下的所有自由度,近似模拟ASME Configuration a的位移边界。分两种类型设置削弱参数:(1)等效削弱参数E*和υ*;(2)各向异性弹性模量矩阵,目的是考察两类模型在面内载荷和弯曲载荷作用下的变形和应力差异,采用Option A计算等效削弱参数。其中类型1(-iso)的模型设计数据见表5,类型2(-ani)的模型设计数据见表6。以模型1-iso为例显示有限元模型的网格划分及边界条件设置,见图2。 表5 模型设计数据(类型1)Tab.5 Design data for models (Type 1) 表6 模型设计数据(类型2)Tab.6 Design data for models (Type 2) 2.2.1 验证各向异性弹性矩阵的设置 由式(29)可得: (30) 式(29)中等式左侧,其余5个应力应变关系采用同样方法验证,这里不再赘述,因此该模型的材料设置是正确的。 这里需要说明:(1)由于材料的各向异性弹性模量基于笛卡尔坐标系,式(30)在笛卡尔坐标系下所有节点均成立,但对于柱坐标系,只有在Y=0°的节点可以满足式(30);(2)图3中第1和第2张图表明,柱坐标下X方向和Y方向的应力分布并非完全轴对称状态;(3)理论推导过程忽略等效圆平板边界效应对内部区域应变应力的影响,对于一个无限大的圆平板笛卡尔坐标系下的矩阵是适用的,但在实际管板模型中,若圆平板的直径较小,则边界效应可能会使得平板边缘的等效应变和应力偏离正确值。 图3 柱坐标系下的X,Y,Z方向的应力分布云图 图4 距离中心20 mm节点的应力和应变 2.2.2 各向同性和各向异性弹性模量矩阵对应力和变形的影响 对类型1和类型2共10个模型进行应力分析,得到每个模型在柱坐标下,Y=0°方向,从管板中心到管板边缘下表面所有节点在柱坐标下X,Y,Z方向应力及Z方向的变形,将同样厚度的模型作为一组进行对比,例如模型1-iso和1-ani为一组,其应力结果和Z方向的变形结果见图5,6。 图5 模型1-iso和1-ani应力对比Fig.5 The comparison of stresses betweenModel 1-iso and Model 1-ani 表7列出了同样厚度的两类模型之间,X方向(平板中心和平板边缘)和Y方向(平板中心和平板边缘)的应力以及Z方向(平板中心)变形的数值对比,从相对误差可以看出,除去个别偏差较大值外,两类模型的应力和Z方向变形基本随参量h/p的增加而误差增加,这与前述理论对比吻合,随h/p增加,Z方向有关的Ez*和Gz*等参数对结果的影响越大,因此对于厚管板(h/p≥2)的模型,应采用各向异性弹性模量矩阵进行应力计算。 图6 模型1-iso和1-ani Z向位移对比Fig.6 The comparison of displacement in Z directionbetween Model 1-iso and Model 1-ani 表7 两类模型应力结果对比Tab.7 The comparison of stresses in the two types of models 本文总结了前人关于多孔板等效圆平板的研究成果,介绍了ASME Ⅷ-2附录5-E中计算等效削弱参数的两种方案Option A和Option B的理论来源。其中Option A与前人理论研究成果和试验数据相符,适用范围广,无论何种厚度的管板和载荷类型,均可以采用Option A计算等效削弱参数。Option B区分平面应力状态和一般平面应变状态,更加灵活。而当管板处于一般平面应变为主时,即h/p≥2时,由于Option A和Option B的理论基础相似,两种方案得到的等效削弱参数接近。当h/p<2时,Option A和Option B计算得到的参数偏差较大。对于常见管板多为h/p≥2,平面应变状态为主。 对ASME规范各向异性弹性模量矩阵进行理论分析,并指出基于笛卡尔坐标系的弹性模量矩阵在有限元模拟中应注意转换,材料参数设置应在笛卡尔坐标系下使用,并且应注意模型的Z向应与柱坐标Z方向一致。5组圆平板模型对比了各向同性弹性模量和各向异性弹性模量对应力和变形的影响,随着h/p增加,Z方向的削弱参数对应变和应力影响增大,因此,管带系数μ*=0.25附近,对于h/p≥2的管板,建议考虑各向异性弹性模量矩阵进行应力分析。1 Option A与Option B的异同点
1.1 Option A方案


1.2 Option B方案

1.3 Option A与Option B的区别与联系

2 各向异性弹性模量矩阵
2.1 理论推导

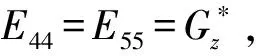
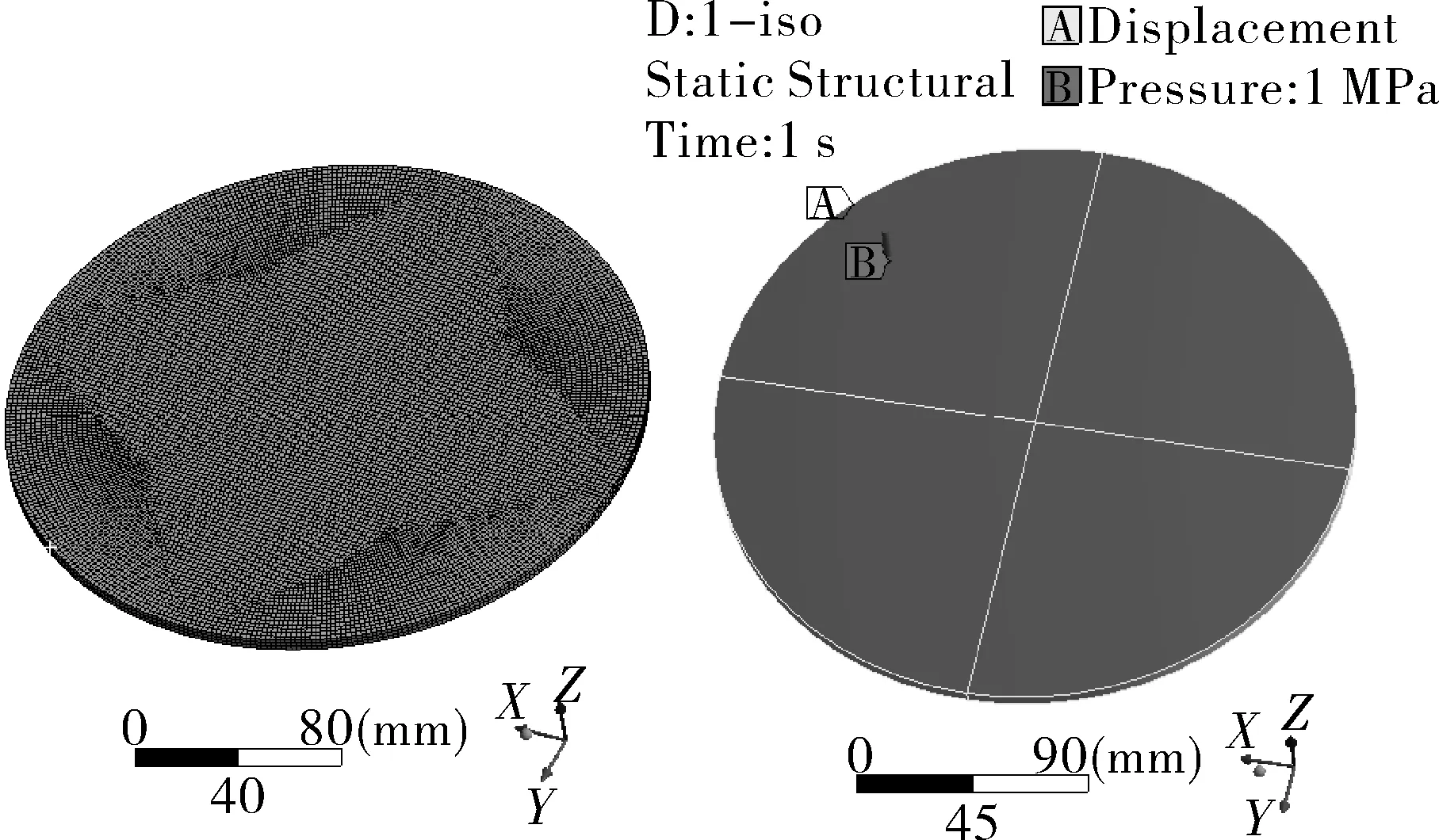
2.2 各向同性和各向异性弹性模量的区别







3 结论

