在线场景更新的多阶段非线性模型预测聚合反应控制

陈显锋,孙京诰,张海峰

(华东理工大学信息科学与工程学院,上海 200237;华东理工大学能源化工过程智能制造教育部重点实验室,上海 200237)

1 引言

出于提高化工生产效率的目的,复杂化工过程控制的经济性指标被愈发重视,且此类系统通常伴随强非线性、工艺约束条件复杂等特性,导致控制系统设计极具挑战.为了应对这些挑战,非线性模型预测控制(nonlinear model predictive control,NMPC)利用过程数学模型,采用在线优化的方式,将操作约束、系统非线性及经济性指标等多个方面同时考虑在内,以确定最优控制输入[1].然而,经济性指标达到最优往往伴随着系统状态运行于可行域的边界[2],进而导致系统性能显著恶化,甚至在模型不确定性的影响下造成经济损失和安全问题[2-3].

考虑到复杂系统存在严格的状态量及输出量约束,额外的鲁棒性裕度应被引入以抵消模型不确定性的影响.最大最小方法一定程度上增强了NMPC的鲁棒性[3],该方法通过最小化最坏情况下的损失函数获取最优控制输入轨迹,同时确保可靠的约束满足,但优化是以开环方式针对最坏情况执行的,并未利用任何的反馈信息,通常导致解决方案较为保守.

在文献[4]中作者认为不确定性的有效处理需要反馈模型,因此通过求解开环优化问题计算的控制输入轨迹并不是最优的.Lucia等人提出的多阶段非线性模型预测控制(multi-stage nonlinear model predictive control,MSNMPC)[5]提供了一种利用反馈信息闭环优化的思路,该方法通过将预测时域上的不确定性传播用离散的场景树表示,然后针对不同的场景计算不同的控制输入轨迹.即MSNMPC式明确考虑了新的信息在未来的时间步中将变得可用,并且新的最优控制输入将被重新计算.这一概念在随机规划中通常被称为追索权[6],是不确定条件下最优决策的一个重要性质.

对于各种应用场景,MSNMPC方法已被证明比传统的最小-最大NMPC方法具有更低的保守性[7-9].且文献[10]中给出了MSNMPC方法的稳定性和递归可行性的严格证明.尽管如此,为了确保场景树中考虑的所有场景都满足鲁棒性约束,MSNMPC提供的解决方案仍将是保守的.选择场景树中不确定性的离散实现场景的常用方法是使用不确定参数的最大值、最小值和标称值的组合.如果不确定参数考虑的范围很大,则场景树建模的跨度也很大,对于时不变的不确定性参数,该解决方案将是保守的,尽管与传统的最小-最大NMPC相比不那么保守.

半间歇聚合反应过程具有非线性、不确定性等复杂特性,如何在确保约束满足的条件下(如:温度约束、安全约束等),提升过程的生产效率是目前研究的重点[11].不同批次反应过程之间相对独立,不确定参数在每个新的批次中是未知的常数(或较小范围波动),对于这类问题可能需要从自适应框架而不是鲁棒框架来处理,典型的自适应控制框架涉及参数估计器的使用,该参数估计器在线调整不确定参数,使得它渐近收敛于真实系统[12].受到文献[13-14]中自适应鲁棒方法的启发,本文采用更新不确定性特征,而非不确定性参数的方法实现低保守性的不确定非线性系统的鲁棒预测控制.

对应于自适应鲁棒方法估计不确定性参数的所有可能值的不确定集的处理方式,本文提出了一种基于递归贝叶斯概率方法更新场景树,该方法在每个时间步计算场景树中每个场景的模型预测信息与实际过程输出测量信息的偏差,为不同场景计算和分配贝叶斯权重;然后利用权重信息以固定步长更新场景来缩小场景树的跨度.即通过计算不同不确定性离散实现场景的贝叶斯权重,逐渐消除不确定性集合中发生概率较低的情况,使得场景树的跨度随着时间的推移而缩小,从而降低标准的MSNMPC方法的保守性.总而言之,这是一种基于可用度量和模型预测在线更新场景树的直观方法.

2 鲁棒的MSNMPC框架

MSNMPC是一种闭环鲁棒控制方法,如图1所示,它将不确定性参数在时间上的演变过程通过场景树的形式表示,该树在每个预测步骤中针对不确定性极值的组合进行分支,其中不确定性可能是参数扰动或外界干扰.假设过程全状态可测量或估计,由树结构可以看出未来的控制输入可根据先前的状态信息做出调整,在一定的范围内抵消不确定性的影响.场景树结构不一定代表时变的不确定性或干扰,但它反映了一个事实,如果不确定性在当前采样时刻是未知的,那么在下一个采样时刻也是未知的.因此一个随时间变化的新的场景树必须被考虑.

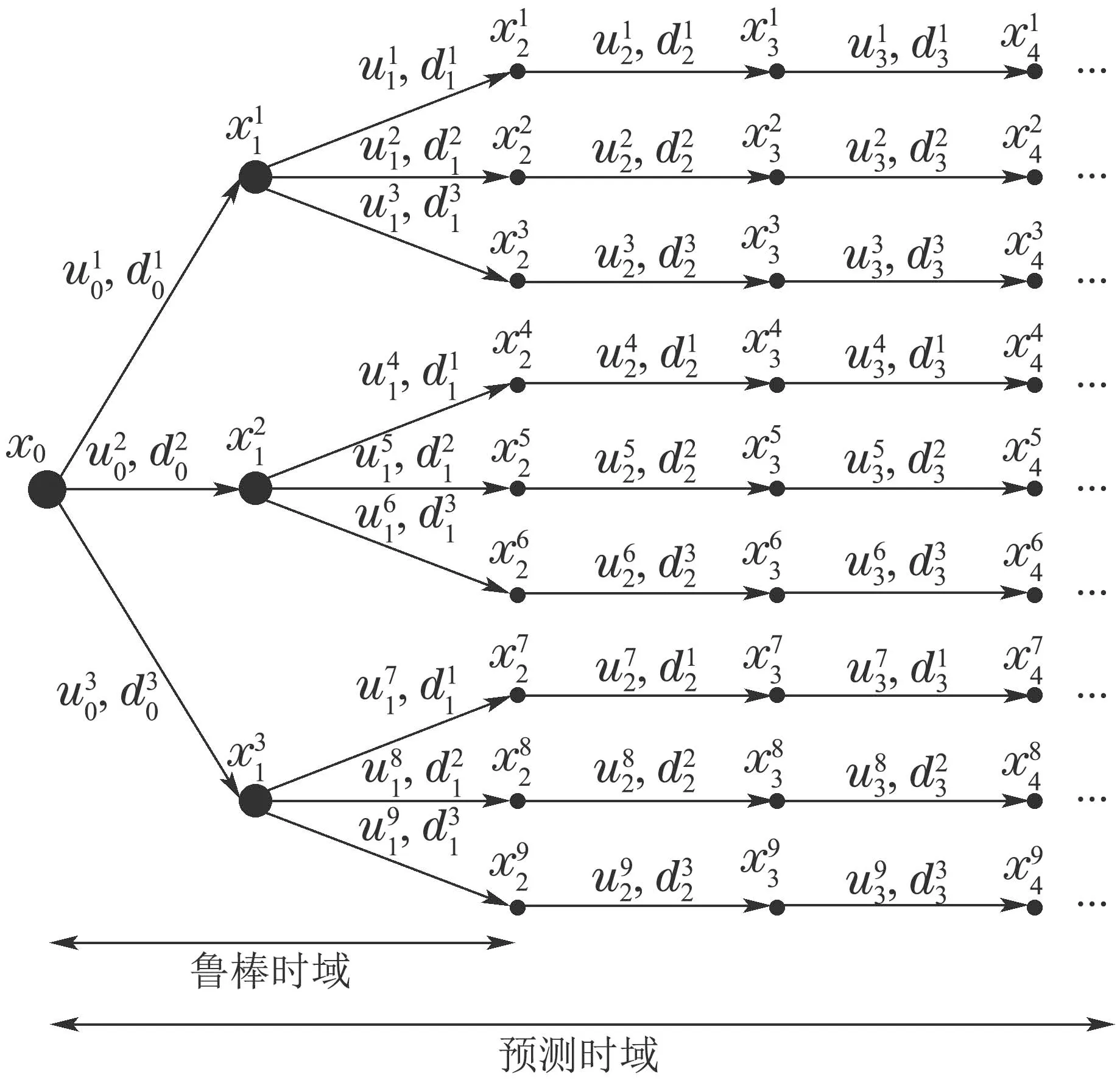
图1 MSNMPC的场景树结构图Fig.1 Scenario tree structure of MSNMPC

在场景树设定下,假设具有不确定性的非线性系统的离散时间式如下所示:

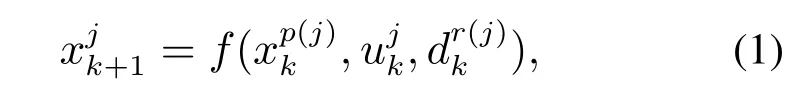
由上式可知时间步k+1的状态是关于前一时间步的状态,控制输入以及不确定性的函数.假设场景树在所有节点上具有相同数量的分支,在时间步k由给出不确定性的S个不同可能值.Si表示从根节点x0到其中一个叶节点的第i个场景.构建场景树的合理策略是将不确定性极值的所有可能组合视为分支.随着预测时域的增加,优化问题的规模呈指数增加.通过假设不确定性在特定鲁棒时域后保持不变,以缩小优化问题的规模[5].这种简化的主要思想是,由于NMPC的滚动时域特性,对未来较远时刻非常精确地建模并不是关键,因为最优控制输入都将在下一个采样时刻被重新计算.

在每个时间步k基于场景的多阶段式的最优控制问题可以表示为

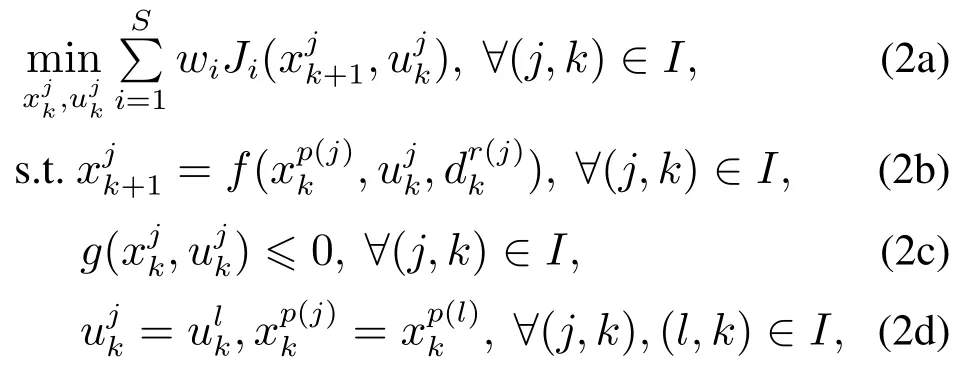
其中:I表示场景树所覆盖的节点相对应的所有索引组合(j,k),S表示场景的数目,wi为每个场景Si对应的权重.表示对场景树的每个节点的状态和控制的非线性约束.为了正确地表示实时决策问题,控制输入不能预测在相应决策点之后实现的不确定性的值,因此非预期约束式(2d)要求具有相同父节点的控制输入也必相等,以便施加正确的控制器因果关系.对于半间歇聚合反应过程,带有权重wi的每个场景Si的损失函数定义如下:

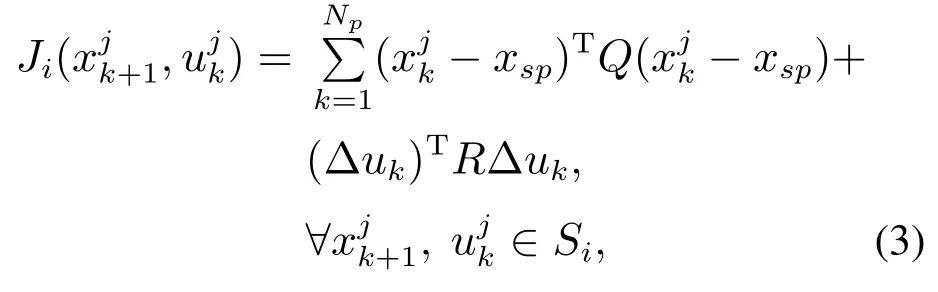
其中:Np为预测时域,损失函数由状态变量跟踪的惩罚项和控制变量变化的惩罚项组成,Q和R分别为对应的对角加权矩阵.

3 在线场景更新的MSNMPC

传统的MSNMPC通常选择不确定性参数极值的组合作为场景树中不确定性传播的场景.一旦确定了不确定性参数及其范围,固定的场景树也就随之生成.如果不确定性参数变化范围很大,场景树的表示范围也会很广.但对于时不变的不确定性参数,该解决方案显然过于保守.

提出的在线场景更新的MSNMPC方法,其结构如图2所示.在每个时间步k中,通过求解式(2)中的优化问题获取最优控制输入应用于实际过程和S个场景的预测模型中,然后根据每个场景的模型预测信息y(k,j)和实际过程的测量信息yk计算场景偏差,利用场景偏差计算贝叶斯概率权重,根据权重信息以固定的步长在线更新场景以预测不确定性值的真实实现,使场景树建模逼近不确定性的真实值.

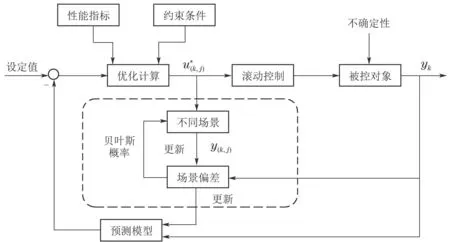
图2 MSNMPC在线场景更新方法Fig.2 MSNMPC online scenario update method

在半间歇聚合反应过程中,不确定性参数在新的批次中是未知的,如果仅考虑传统的组合方案,可能导致该方法趋于保守,性能退化.因此需要考虑一种自适应的在线场景更新方法,在每个时间步k中,依据已经获取的信息推算该场景对应的不确定性值与实际过程中不确定性真实值的差距,采用自适应机制更新场景树中可能性较低的场景来缩小场景树的跨度,使控制器性能能够随着时间的推移逐渐提高.

对于实际的不确定性半间歇聚合反应过程,首先确定不确定参数的数量及相应的取值范围,构造初始不确定性集.然后利用在线场景更新的MSNMPC算法缩小场景树对应的不确定性集D.该算法的具体实施步骤如下所述:

步骤1初始化每个场景的权重P(0,j)=1/S,j∈{1,···,S},其中S为场景树的总场景数,初始化不确定性集合D;

步骤2计算当前时间步k中S个场景对应的模型预测值y(k,j)

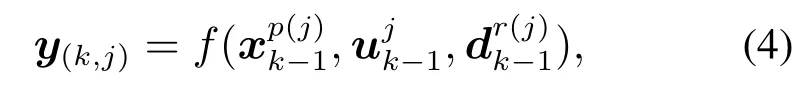
然后根据当前时间步k的模型预测值y(k,j)和过程测量值yk和计算残差ε(k,j),其式描述为

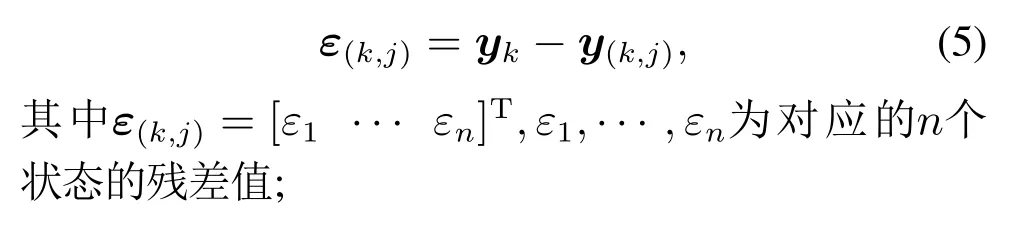
步骤3利用残差信息ε(k,j)和前一时间步的每个场景权重P(k−1,j)计算当前时间步k的贝叶斯概率权重P(k,j),其式描述为

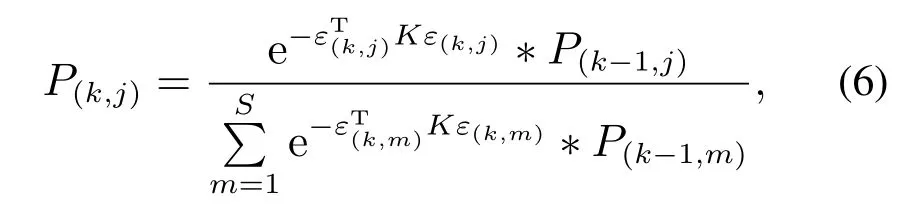
其中K是一个加权矩阵,通常选择为对角线,可以看作是残差协方差的倒数:

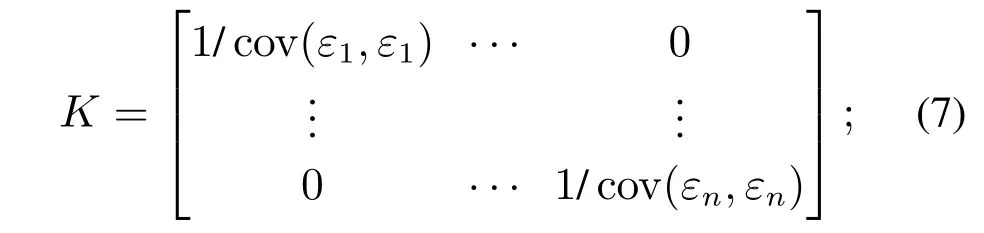
步骤4根据当前时间步k的每个场景的贝叶斯概率权重P(k,j),找到S个场景中最大的权重对应的场景pmax和最小的权重对应的场景pmin:

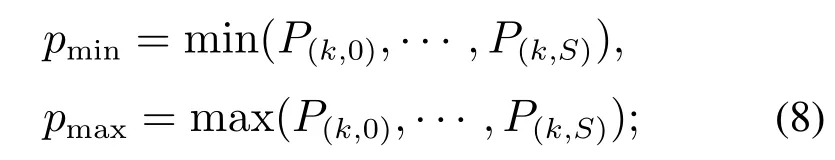
步骤5通过将最不可能的场景pmin移向最有可能的场景pmax来更新pmin和Dk+1.如下式表示了场景树的更新过程:

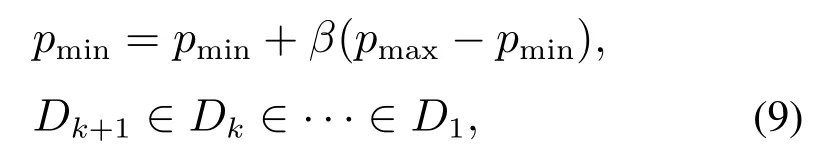
其中β为自适应步长,可以控制不确定性集缩减的速度,应该保持在一个较小范围;

步骤6在下一个时间步k+1,根据新的不确定集合构建的场景树求解MSNMPC最优控制问题获得最优控制动作:

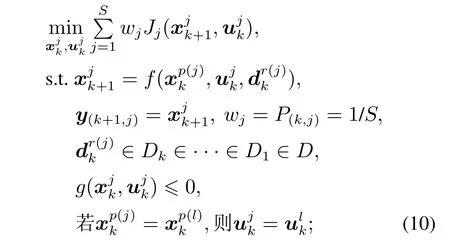
步骤7重新初始化每个场景的初始权重P(0,j)=1/S,j ∈{1,···,S};

步骤8重复步骤2-7,直至批次反应过程结束.

4 半间歇聚合反应模型

本文以实际工业半间歇聚合反应器模型(如图3所示)为研究对象,该系统由一个进料单体的反应器组成,反应器配有一个夹套和一个外部热交换器,它们可以用来控制反应釜内温度.根据物料守恒和能量守恒,该过程模型由8个常微分方程组成:

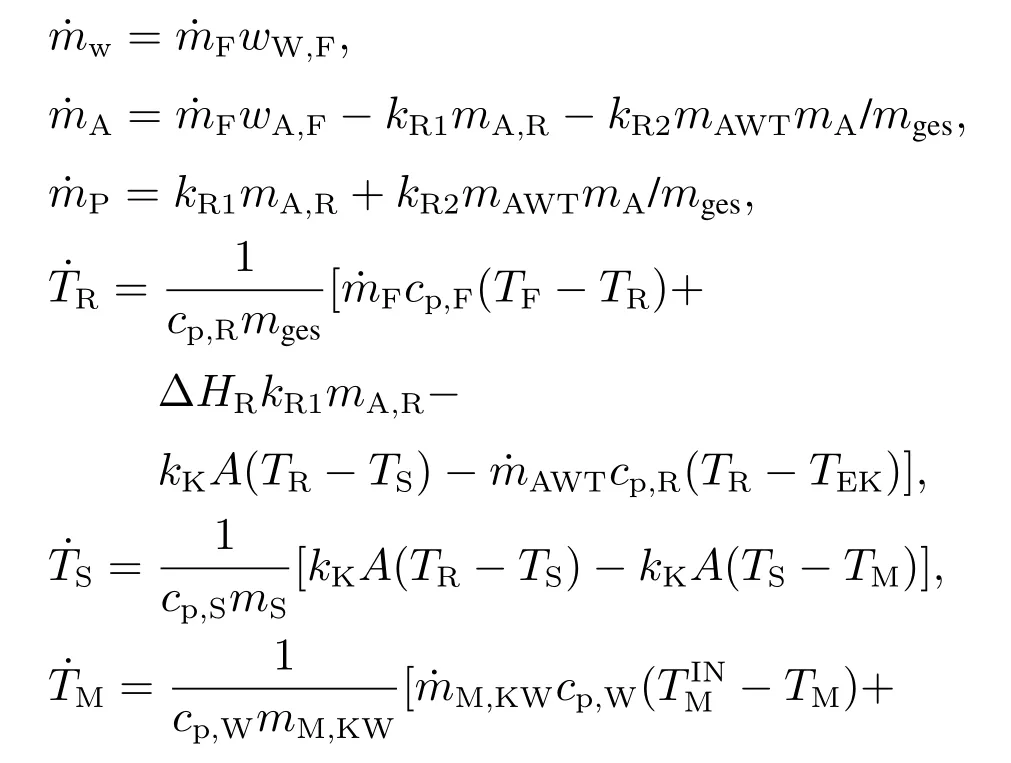
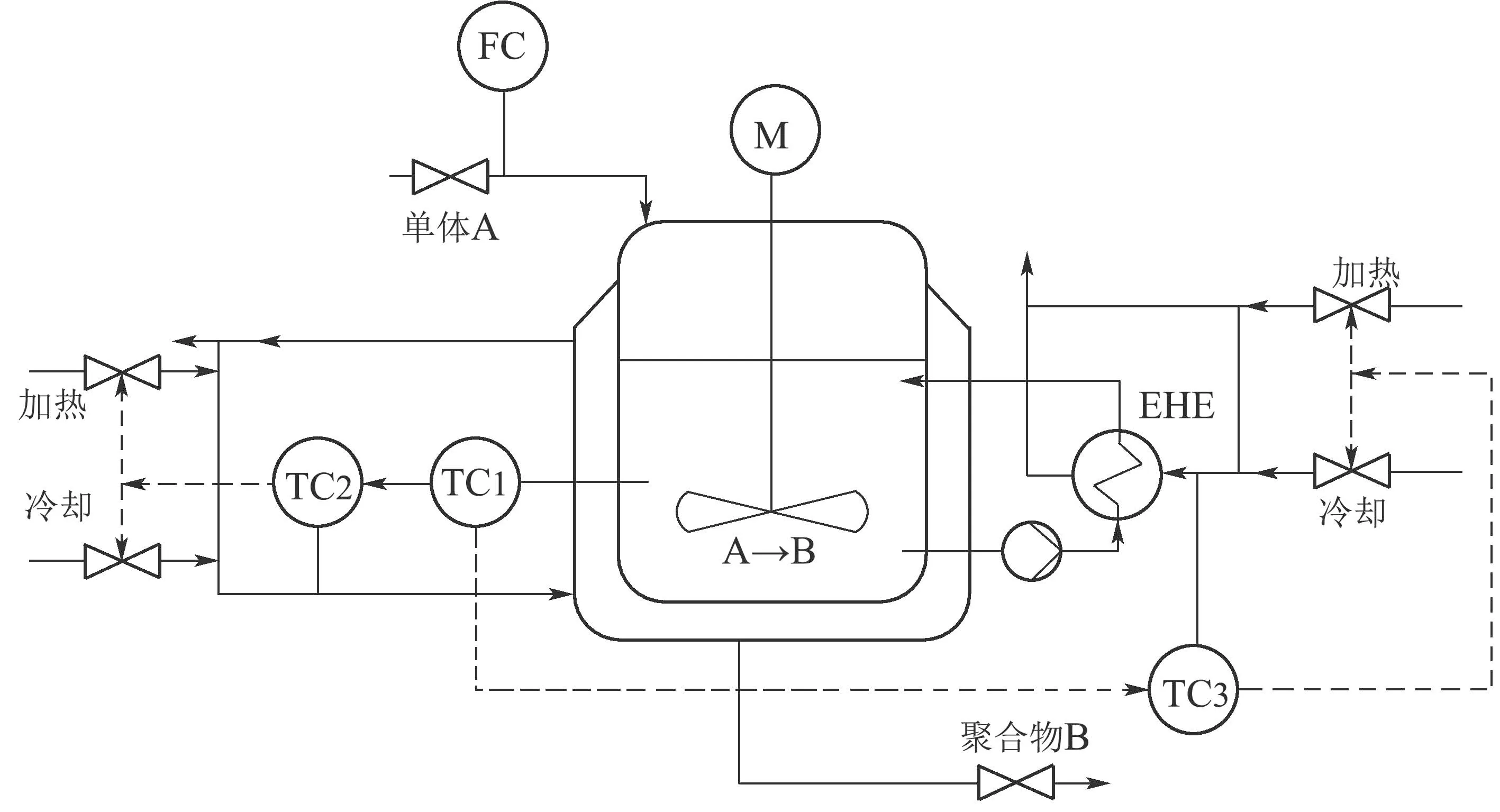
图3 半间歇聚合反应工艺图Fig.3 Semi-batch polymerization process diagram

5 仿真分析

基于上节中的半间歇聚合反应模型,考虑的不确定性参数为反应热焓ΔHR和反应速率k0,它们的值在标称值的±30%内变化,因此ΔHR的不确定范围为[665,1235],k0的不确定范围为[4.9,9.1].不确定性值在每个新的批次中是时不变且无法测量估计的.场景树中考虑不确定性的离散实现场景数为S=5,对应于两个不确定性参数的最小值和最大值的组合.考虑的预测时域为Np=15,鲁棒时域为Nr=1,采样时间tstep=50 s.

考虑每个场景Si的经济型损失函数如下:

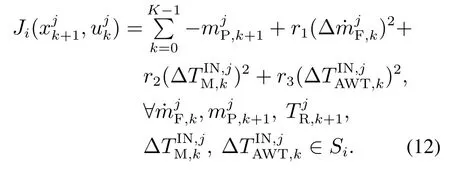
其中:q,r1,r2和r3分别为10000,0.004,0.02和0.004.本文求解过程首先采用有限元正交配置方法进行离散化处理,然后利用CasADi[15]工具包中的IPOPT求解器解决由此产生的非线性规划问题.

首先,将提出的在线场景更新的MSNMPC方法与标准的NMPC方法和标准的MSNMPC固定场景树方法应用于半间歇聚合反应模型中,其中在线场景更新的MSNMPC方法考虑的更新步长设置为β=0.05.在该仿真批次中不确定性参数考虑的真实值为ΔHR=950 kJ/kg,k0=7.仿真结果如图4所示.可以看出,标准NMPC(黑色点线)最先完成规定产量的产品,但由于未考虑不确定性的影响违反了反应器内温度TR的约束.而另两种方法由于将不确定性考虑到了优化问题中,因此可以很好的将反应器内温度TR和安全温度Tadiab控制在约束范围内.并且,在线场景更新的MSNMPC方法(绿色点虚线)的批次反应时间为1.75 h相比于标准MSNMPC(蓝色虚线)的1.861 h缩短了0.111 h,批次生产效率得到提升.

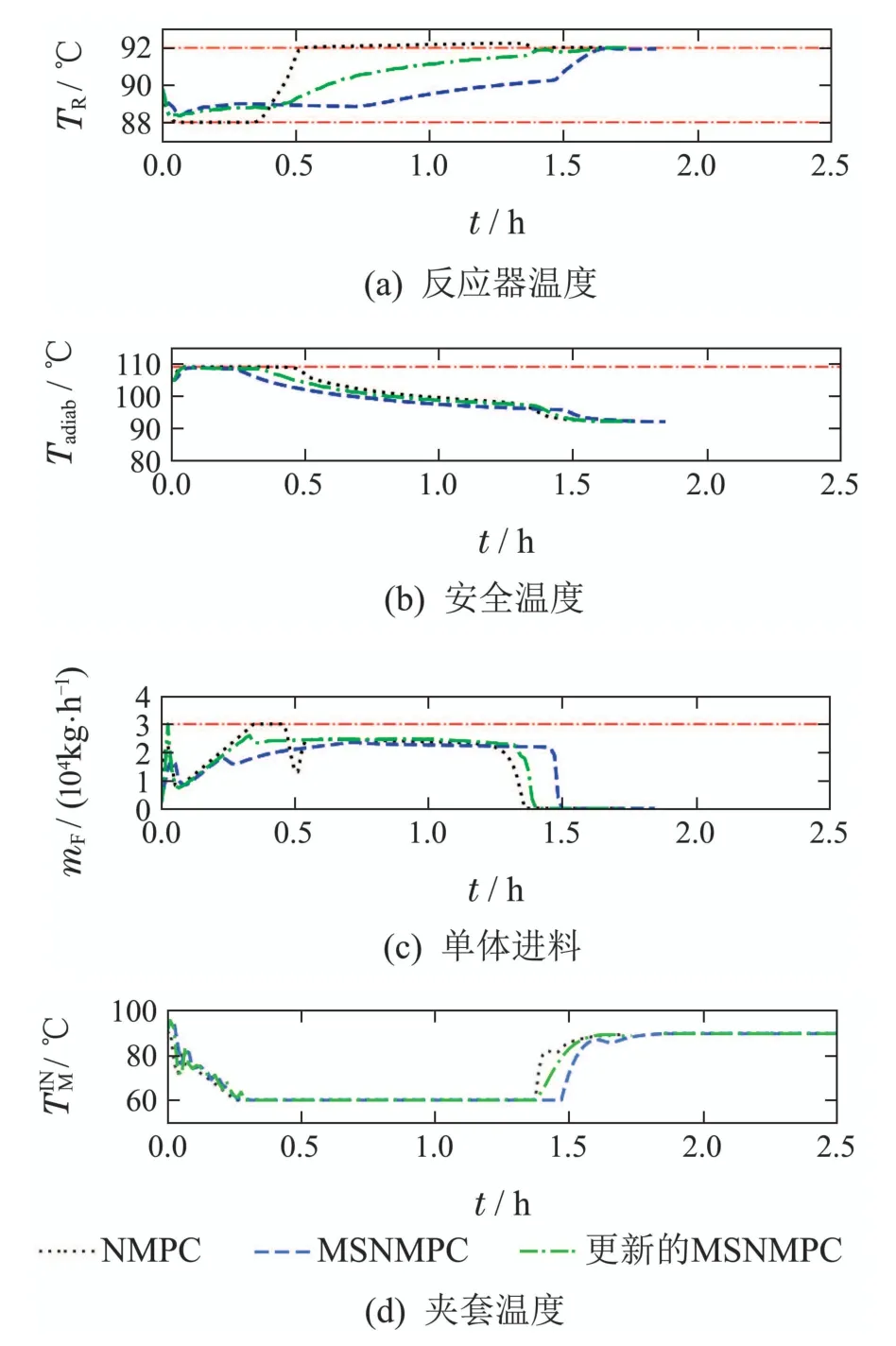
图4 不同方法的单批次反应仿真对比图Fig.4 Single batch reaction simulation comparison chart of different methods

场景树的更新过程如图5所示.由于控制器的最优控制问题是所有场景的综合损失函数最小,随着场景树的跨度逐渐缩小逼近不确定性的真实实现,优化问题求解的控制输入也在逐步逼近最优轨迹,控制器性能得到提升,从而缩短批次反应时间.

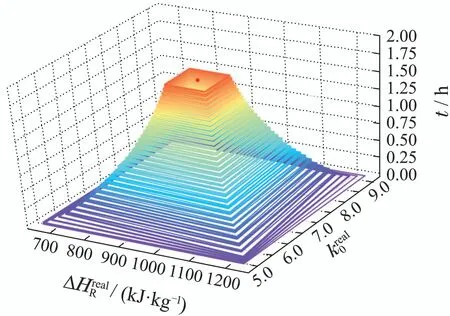
图5 场景树的在线场景更新过程Fig.5 Online scenario update process of scenario tree

为了验证在线场景更新的MSNMPC方法的通用性,随机选取100个不同批次的不确定性值进行测试(图6).仿真结果如图7所示,7(a)和7(b)分别表示100个不同批次的不确定性值,7(c)为在线场景更新的MSNMPC方法与标准MSNMPC方法在对应批次过程的反应时间对比图.可以看出在线场景更新MSNMPC方法对应的批次反应时间更短.

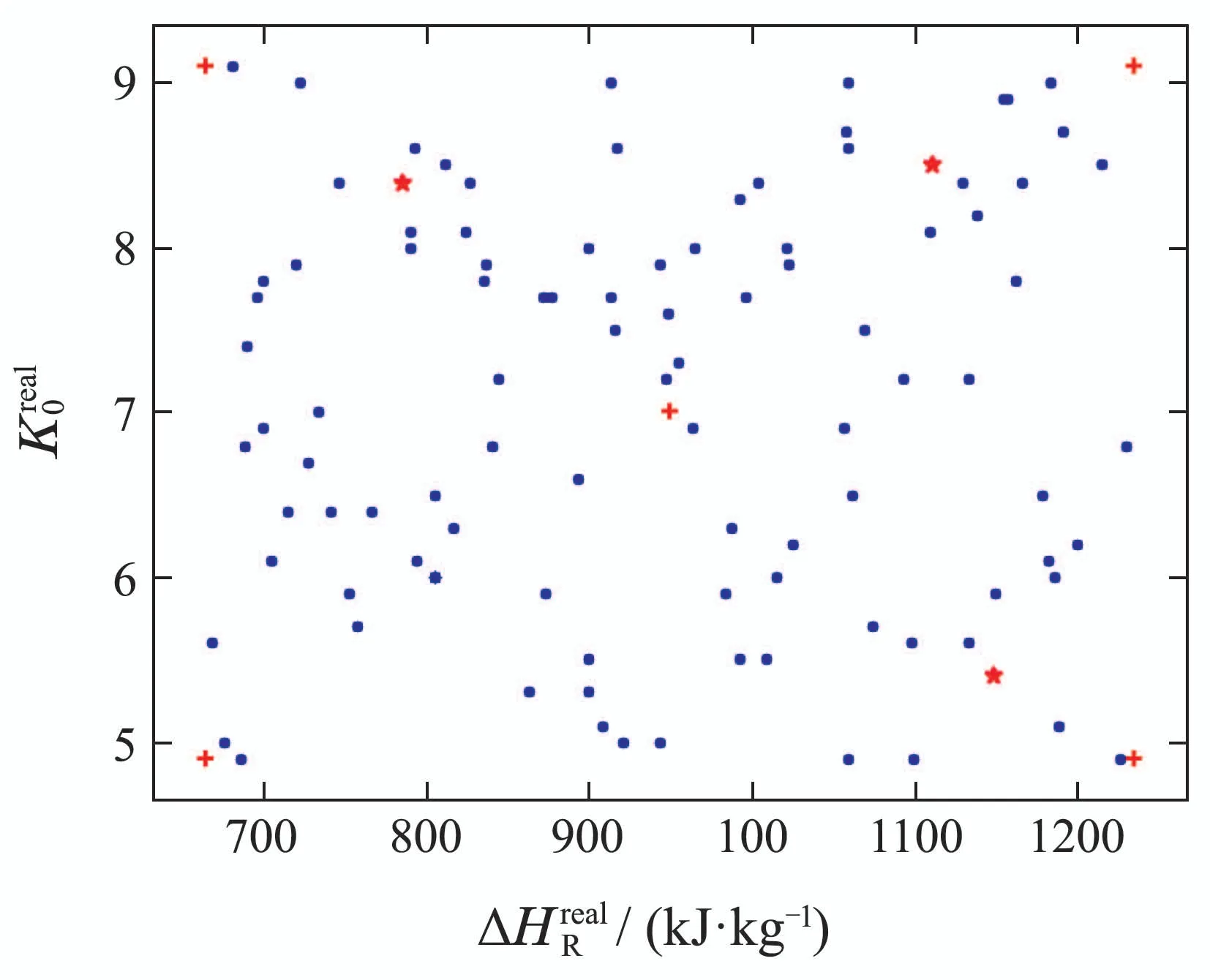
图6 100个不同批次的不确定性真实实现Fig.6 Real realization of uncertainty in 100 different batches

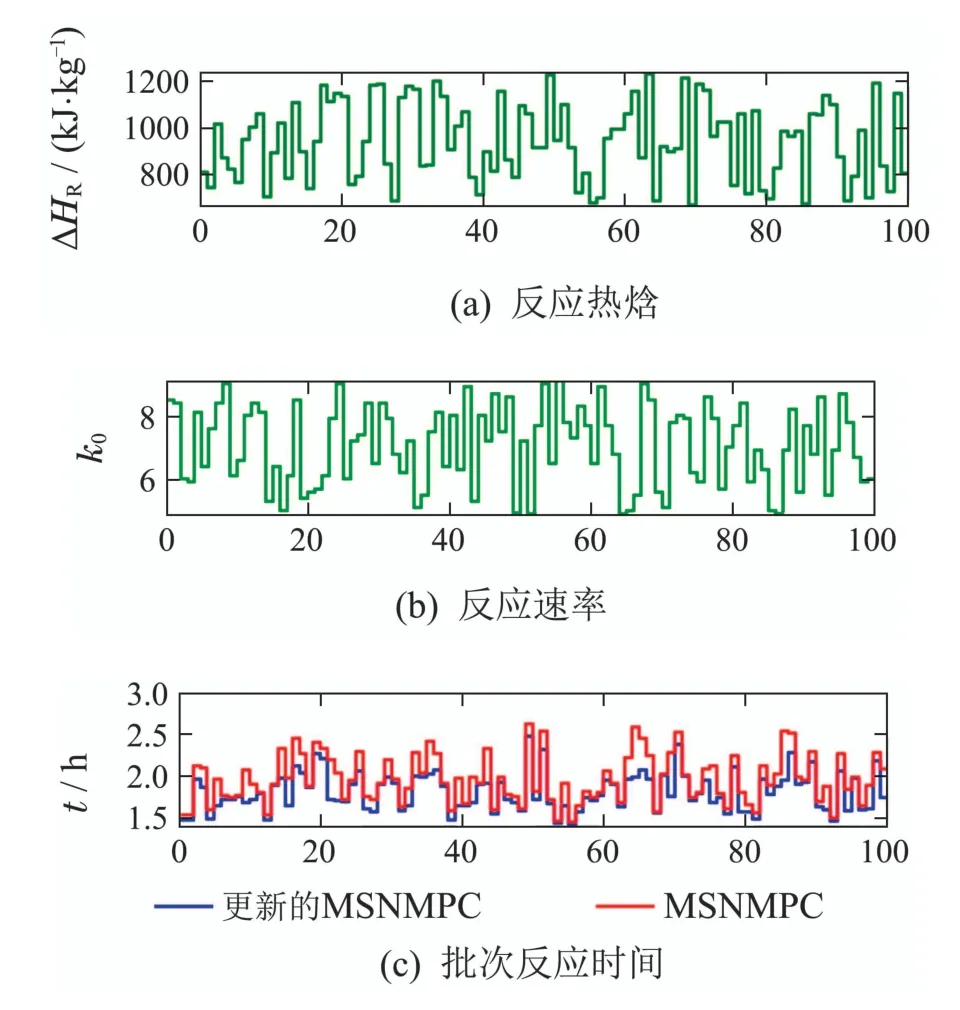
图7 100个不同批次过程仿真对比Fig.7 Comparison of 100 different batch process simulations

由表3的批次反应时间对比数据可知,标准NMPC因未考虑不确定性因素,在许多不确定性的真实实现过程中会出现大幅度的违反约束,导致控制不可行.而在线场景更新的MSNMPC方法与标准MSNMPC方法对于不同场景均可满足约束要求,完成反应过程,且前者在性能上更优.对于100个不同批次反应过程,标准MSNMPC方法的平均批次时间为1.961 h,而在线场景更新的MSNMPC 方法仅为1.807 h,缩短了0.154 h,进一步说明本文提出方法的有效性和优越性.

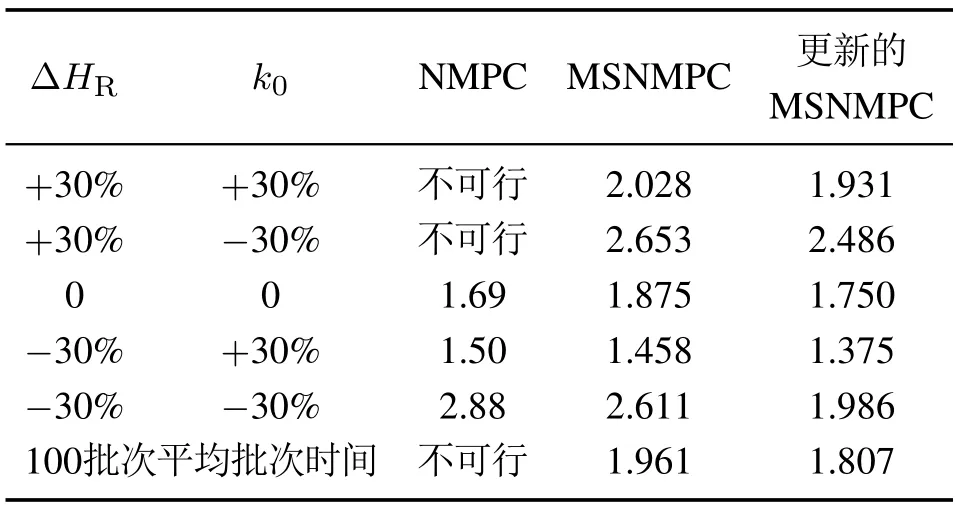
表3 不同批次的反应时间对比Table 3 Reaction time comparison of different batches

为了更好理解场景更新过程,选取图6中∗标记的3个不同批次过程,其场景更新过程如图8所示.

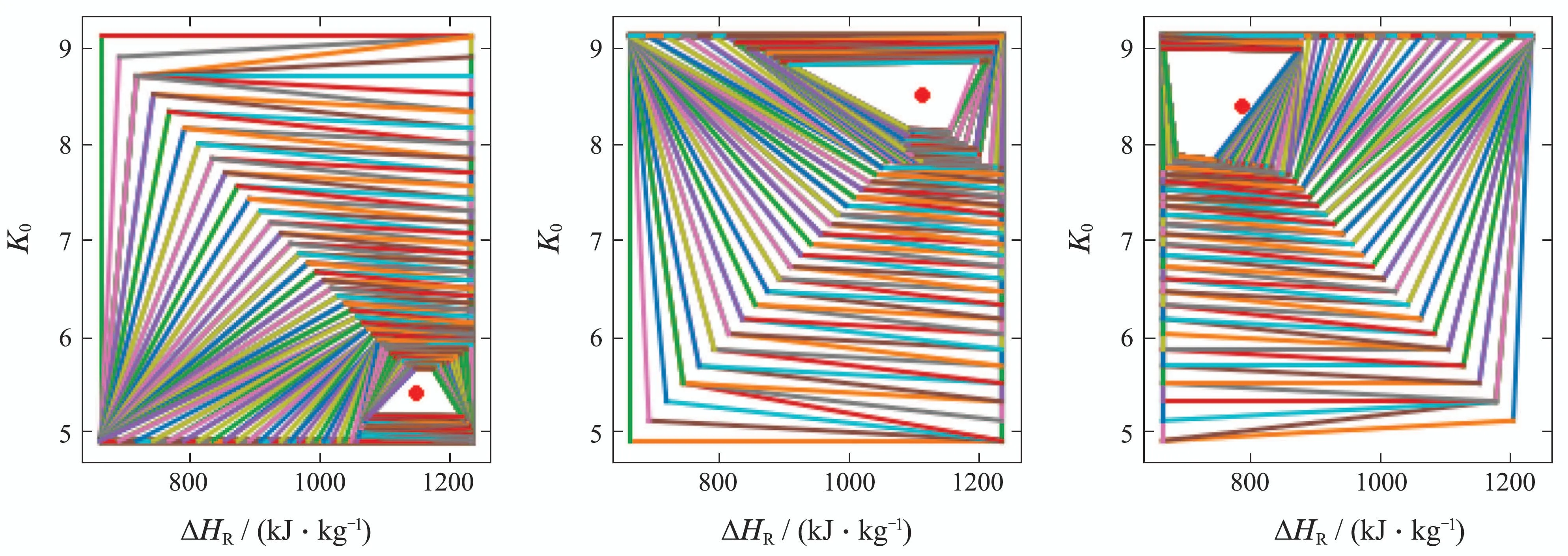
图8 不同批次过程的场景更新过程Fig.8 Scenario update process of different batches

6 总结

本文基于MSNMPC的场景树框架,针对时不变不确定性参数不能直接估计的情况下场景树生成的合理性问题,提出一种基于贝叶斯概率加权的在线场景更新的MSNMPC方法,通过计算每个场景的模型预测信息和状态输出测量信息的偏差,为不同场景计算和分配贝叶斯概率权重,然后在线更新场景树中不确定性的离散实现场景,缩小场景树的跨度,降低了标准MSNMPC方法的保守性.通过对半间歇聚合反应模型的仿真结果表明,与标准MSNMPC方法相比,在线场景更新的MSNMPC方法在确保约束满足的条件下,针对多个不同批次的不确定性真实实现过程,具有更好的控制性能,更短的批次反应时间,从而提升提升了过程的生产效率.