一种基于齐次系统理论的二阶离散超螺旋控制算法

陈维乐,都海波

(合肥工业大学电气与自动化工程学院,安徽合肥 230000)

1 引言

滑模控制方法具有设计简单、强鲁棒性等优良性质,因此受到广泛的研究和应用[1-6].然而,早期的一阶滑模控制存在着一些不足,尤其是由不连续性带来的抖振现象.后来,一些学者提出了二阶滑模控制和高阶滑模控制[7-13],二阶滑模控制和高阶滑模控制是一阶滑模控制的推广,既有传统一阶滑模强鲁棒性的特点,同时大大消除了抖振,因此得到了越来越多的关注.在二阶滑模控制算法中,超螺旋算法(supertwisting algorithm,STA)因其良好的性质得到广泛的研究和应用[11-20].

以上分析的滑模控制问题都集中在设计连续时间形式的控制器上.然而,在实际中,越来越多的控制器实现是基于数字计算机的采样控制方式[21-22],因此对离散时间下的滑模控制,即离散滑模控制(discretetime sliding mode control,DSMC),进行设计和分析具有重要意义.离散滑模控制在不同采样间隔内控制信号“冻结”,固有的有限开关频率将导致抖振(锯齿形)运动[23],使得使用不连续符号函数的有限时间收敛的性质不再成立.

在此背景下,主要有二种设计离散滑模的方法.其中一种是离散时间设计方法,首先对动力系统进行离散化,然后在离散时间域中设计滑模面,这种设计很大程度上是因为采用了较大的采样周期,其动力学和连续情况下有很大的不同.在文献[24]中研究了拟滑动模态和拟滑动模带,严格定义了有关离散滑模控制的术语,并基于一种趋近律方法建立了单输入离散时间系统的一个新的趋近条件.由于离散化的影响,不可避免的要对扰动进行估计,以增强系统的鲁棒性.文献[25-26]提出了带扰动补偿器的离散趋近律,从而减小了抖振,提高了控制精度.文献[27-28]研究了基于高阶滑模的离散微分器(观测器).另一种是连续滑模控制的离散化,其中的滑模设计是在连续时间域中进行的,然后通过离散化实现.文献[29-30]分别研究了离散化对基于等效控制的单输入和多输入滑模控制系统动力学行为的影响.文献[31]研究了具有匹配不确定性的基于等效控制的滑模控制系统的离散化行为,研究了具有匹配常数和周期不确定性的系统的一些固有的动态周期特性.文献[32]将连续终端滑模控制离散化,给出了系统稳态的显式有界性,建立了控制参数与稳态有界性之间的关系,证明离散时间的终端滑模系统比离散时间的线性滑模系统能提供更高的输出跟踪精度.

本文的主要目的在于研究离散超螺旋控制算法并加以改进.文献[27,33]等已证明离散超螺旋控制算法的控制精度为O(T2),然而在这些论文中,并没有完全考虑到有限开关频率的影响,即假设2.在此意义下,能否对标准超螺旋算法加以改进,提高控制精度具有重要研究价值.本文的主要贡献是利用齐次系统理论在标准超螺旋算法的基础上增加一个参数,使得原来的符号函数项转变为连续非光滑项,设计了离散非光滑控制器(discrete-time non-smooth controller,DNC),从理论上分析了影响控制精度的本质原因,并在此基础上对附加参数的选择进行了分析,揭示了本文设计的改进离散非光滑控制器能提供比离散超螺旋控制器(discrete-time super-twisting controller,DSTC)更高控制精度的原因.最后,仿真验证了理论的正确性.

2 预备知识

这部分主要介绍一些定义和引理,以便于之后的证明和解释说明.

定义1[34](Sig函数) 为了便于书写,定义于扩张(r1,···,rn)有齐次度k.

引理1[36]考虑如下系统:

其中f(·):Rn →Rn是一个连续函数.假设存在一个正定连续函数V(x):U →R,有实数c>0和α ∈(0,1),并且存在一个包含原点开区域U0⊂U使得˙V(x)+c(V(x))α≤0,x ∈U0{0}.那么V(x)将在有限时间内到达0.此外,有限收敛时间T满足

下面的不等式引理是直接借用文献[38-39],或者在此基础上做了一些小小的改进.

3 离散超螺旋控制算法

考虑如下一阶系统:

其中:u(t)是控制输入,f(t)是外部扰动,并且满足以下假设.

假设1f(t)光滑可导,且满足

其中L是已知常数.

本文的主要目标是设计一类采样控制器实现对系统(4)的镇定控制.采样控制方式使用最常见的零阶保持器

其中:tk,tk+1是采样时刻点,T是采样周期.对于采样周期,一般满足下列假设.

假设2已知存在一个最小采样周期T∗,使得

其中T是系统实际能够设置的采样周期.

本文的目标是针对系统(4)设计一种改进的离散超螺旋控制方法,以减小抖振,获得更高的控制精度.首先,针对系统(4),对离散超螺旋算法进行回顾.

具体地,控制器设计为

文献[33]已证明其控制精度可以到达O(T2).接下来,本文将在式(7)的基础上加以扩展,提出一种改进的离散超螺旋控制方法,使系统在采样控制方式下拥有更高的精度.

4 改进的离散超螺旋控制方法

通过运用齐次系统理论,增加了一个参数,扩展了标准离散超螺旋控制方法.本节将证明在采样控制下,本文所设计的改进方法能够使系统有更高的控制精度.

定理1对于一阶系统(4),如果采样控制器设计为

其中-1/2<τ <0,并且增益满足

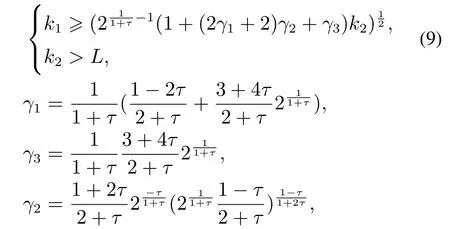
那么系统输出将在有限时间收敛到如下区域:

其中c1,c2是与控制参数相关的常数.

证将控制器(8)代入系统(4)中,可以得到系统状态的精确迭代公式

那么式(11)将转化为

x1(t),x2(t)是系统状态.显然,系统(14)被拆分成了两部分,一部分是连续时间控制器,一部分为采样控制造成的误差.为了便于证明,可以先讨论连续系统部分的稳定性分析,亦即采样时间为0情况下的稳定性分析.具体的证明过程可见附录.

命题1沿着如下的连续时间闭环系统:

其中:γ6为正的常数,ξ=11+τ -x2.

基于命题1,使用与式(17)相同的李雅普诺夫函数,沿着系统方程(14)对V求导,得到

接下来,将证明系统状态将在有限时间内收敛到该集合.

如果系统不在该集合内,这意味着

属于有限时间收敛,因此,无论第2种情况是否发生,都有

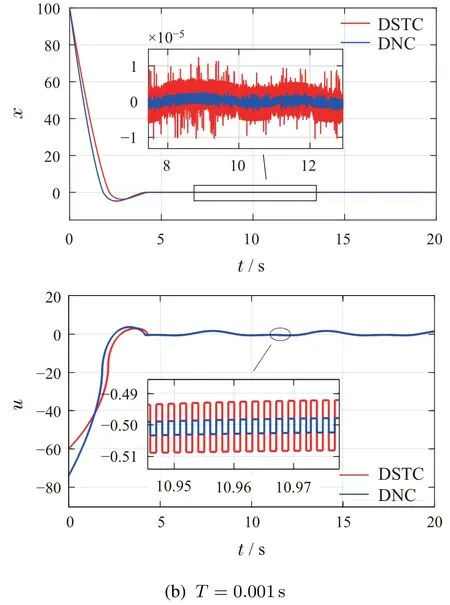
其中常数c满足0

证毕.

注1对于闭环系统(18),即是本文所设计的离散超螺旋闭环控制系统的连续时间形式(亦即采样周期为0),根据齐次系统的定义,当干扰d=0时,该闭环系统对扩张(1,1+τ)具有齐次度τ.因此,本文所提出的离散超螺旋控制算法是基于齐次系统理论设计出的.此外,和传统的连续形式超螺旋控制系统对比,该系统增加了一个附加参数τ,基于式(19),可以看出该额外的参数对系统的稳态误差产生影响.

注2从式(38)可知,系统输出最终将收敛到和所限定的边界内,前者表征着非光滑项带来的抖振影响,后者表征着外在扰动对系统的影响.考虑到−1/2<τ <0,讨论下面2种情况.

1) 如果τ=−1/2,控制器(7)转变为离散超螺旋控制器,那么系统状态边界为

2) 如果τ=0,此时控制器(7)转变为离散线性控制器,状态边界为

由式(38)(47)-(48)可知,在离散系统中,无论是线性项还是非线性项(符号函数)都是针对抖振或者扰动的其中之一有效,而对另一面则会产生较大的误差.一般采样周期远小于扰动,所以一般情况下,离散超螺旋控制器的控制精度上远高于离散线性控制器.

本文在上述2种算法的基础上,采用了一种折衷的方式,引入了非光滑项,通过调节τ在抖振和外部干扰抑制性能之间取得了一种平衡,使得整体稳态误差界变小.τ由下式确定

5 仿真

在仿真中,假设外界扰动为f(t)=-sint+0.5 cos(2t),则=|-cost-sin(2t)|≤2,即L=2.假设最小采样周期满足T∗=0.001 s.为了验证所提算法的高精度,将本文提出的离散非光滑控制器(DNC)与标准的离散超螺旋控制器(DSTC)作比较,并选择较大初始状态,观察最后的误差范围.系统初值:x(0)=100.控制器参数:k1=6,k2=8,v(0)=0,τ由式(49)决定.

系统输出曲线和控制输入曲线如图1所示,可以直观地看出,在不同采样周期下,本文提出的离散非光滑控制器稳定状态时的误差界都显著小于离散超螺旋控制器.此外,图1中系统输出曲线最后的误差界整理在表1中,从表中误差界的大小关系可以看出,通过调节τ的取值可以将误差界显著减小,说明了本文的改进算法可以实现更高的控制精度目标.

图1 在不同采样周期T情况下,离散超螺旋控制器(DSTC)和离散非光滑控制器(DNC)作用下的系统输出和控制输入Fig.1 Under the case of different sampling periods T,the system output and control input under the action of discrete-time super-twisting controller (DSTC) and discrete-time non-smooth controller(DNC)

表1 2种算法下系统最终收敛的误差界及其比较Table 1 The bounds of the final convergence of the system errors under two algorithms and their comparison

6 总结

本文针对一阶系统的采样控制提出了一种改进的离散超螺旋控制方法.首先,在超螺旋控制算法的基础上,利用齐次控制理论,通过调节附加参数来提高控制精度.然后,通过构造合适的李雅普诺夫函数,定量地分析了采样周期和外在扰动对控制精度的影响,并给出了附加参数的整定方法,证明了本文的改进算法精度高于标准离散超螺旋控制算法.最后,仿真验证了理论分析的正确性.

附录 命题1的证明

首先,结合引理2,给出V1的导数为