基于未知输入观测器的多智能体一致性控制

相国梁,郭胜辉

(苏州科技大学电子与信息工程学院,江苏苏州 215009)

1 引言

随着科技的发展,嵌入式计算机的计算能力和通信能力得到前所未有的提高.随之而来的就是分布式或非集中式的设计思想的发展,在软件设计中,专家提出分布式计算、微服务等架构.在硬件设计中,人们越来越认识到多智能体系统的合作工作模式能够以更小的代价完成更复杂的任务.在过去的十多年里,多智能体系统在各类工程系统中得到广泛的应用,如无人飞行器或无人水下航行器的协同控制[1]、以自然界诸多生物群体为模型的群体或集群的集体行为控制[2-3]、多智能体系统的编队控制[4]以及分布式传感器网络和卫星集群的姿态对准[5-6].

近年来,协同控制成为多智能体领域一个重要研究方向.在多智能体系统的分布式协同控制中,每个智能体利用自身的局部信息协同完成全局任务.而一致性控制作为多智能体系统协同控制的一个基础性问题,已经得到了深入研究.一致性控制问题就是设计一致性控制协议使得所有子系统状态达到某个同一值,如文献[7]在电气物理系统中利用一致性控制来自适应地调整虚拟阻抗,来补偿不匹配的线路阻抗,以实现准确的无功功率分配.文献[8]在生物实验中使用血清饥饿法进行细胞周期同步化实验,并进一步研究细胞在细胞周期中发生的事件.因此一致性控制受到了物理、生物、工程等诸多领域的专家关注.文献[9]利用滚动优化控制设计了一般线性多智能体的控制协议.为了减少不必要的计算压力,文献[10]利用降阶控制器实现对输出反馈多智能体的一致性控制.文献[11]考虑了在执行器饱和情况下高阶多智能体的全局最优一致性控制.文献[12]解决一类在切换系统下多代理系统输出同步性问题.文献[13]通过事件触发来实现多智能体的一致性控制.

复杂的工业生产中,各种不稳定性无法避免,导致未知输入和随机噪声同时存在,关注到很多文献仅考虑了未知输入或者随机噪声一种情况,本文考虑未知输入和随机噪声同时存在的情况下实现多智能体的一致性控制.本文利用卡尔曼滤波器设计观测器,针对含有随机未知输入信号的多智能体系统研究一致性控制,使用线性矩阵不等式(linear matrix inequality,LMI)设计一致性协议,最终实现多智能体的一致性控制.本文第2节引出问题并描述图论相关的预备知识;第3节利用卡尔曼滤波器进行未知输入观测器的设计;第4节设计一致性控制协议并且在第5节中设计一个仿真验证算法可行性.

注1本文所用符号皆为规范符号,Rn表示n维欧氏空间,ei表示估计状态误差,矩阵P >0表示P是正定的,矩阵P <0表示P是负定的,1N表示各元素均为1的N维向量,IN表示N维单位矩阵,⊗表示Kronecker积.

2 问题描述与预备知识

定义无向图:G=(ν,ς,A),其中:ν={1,2···,N}表示图中节点的集合,ς ⊆ν×ν属于图中边的集合,A=[aij]是G的权重矩阵,并且aii=0;当(i,j)∈ε时,aij >0.否 则aij=0.Ni={j:(i,j)∈ς}表 示节点的所有相邻节点的集合,节点i的度定义为

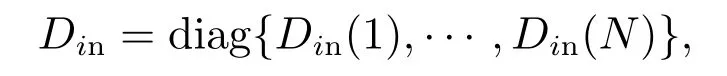
图G的拉普拉斯矩阵定义为L=Din-A.

引理1[21]对应与无向连通图G的拉普拉斯矩阵L具有如下的性质:1)rank(L)=N -1;2)0是矩阵L的一个特征根,且1N为对应的特征向量;矩阵L的其余特征值均为大于零的正实数.根据引理1,存在一个正交矩阵Π,使得

其 中:Λ=diag{0,λ2,···,λN},元 素0,λ2,···,λN对应于拉普拉斯矩阵L的N个特征根.

Leech in his book Principles of Pragmatics published in 1983 defines politeness as forms of behavior that establish and maintain com

考虑由N个非线性节点所构成的网络系统,在考虑系统还有噪声的情况下,令每个节点的动态模型为

其中:xi(k)∈Rn,ui(k)∈Rk,yi(k)∈Rp,εi(k)∈Rm分别表示系统状态、系统输入、可测输出以及未知干扰输入;ξi(k),ηi(k)是独立的零均值噪声序列,它们的协方差分别为Q和R矩阵;A,B,C,D为适当维数的矩阵,其中,B为列满秩矩阵.

假设1非线性函数f(xi(k))满足Lipschitz条件,即存在正常数γ使得

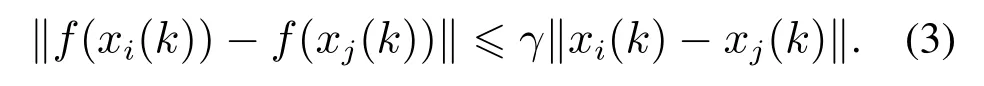
首先考虑由N个非线性节点所构成的网络系统,其中每个节点的动态模型在不考虑系统噪声的情况下为

3 未知输入观测器设计

为了设计未知输入观测器,首先需要消除未知干扰的影响,在满足rank(CD)=rank(D)=rd的条件下,可以完全消除干扰项并实现完全重构.在此条件下,存在M,使得

用M同时乘以式(4)左右两边可以得到

在一般未知输入观测器中,状态反馈矩阵L1的选择只要令系统为稳定系统即可,即使系统极点分配在左半平面.然而这并没有考虑到系统存在噪声的情况.考虑到系统噪声的影响,本文通过配置状态反馈矩阵L1来降低噪声对系统的影响.

由文献[23]可知上述反馈矩阵构造计算方法与卡尔曼滤波算法相同.在实际面对大量数据时,不仅简化计算过程而且降低数据存储量和计算量.

4 基于观测器的一致性控制协议设计

本文由状态观测器(14)的估计信息,设计如下一致性控制协议:

其中K表示控制增益矩阵.

定义同步状态误差

下述为本文提出的一个主要结论.

定理1考虑由N个非线性智能体(2)所构成的连通网络系统.对于给定的拉普拉斯矩阵特征根λi(i=1,···,N),正常数γ,τ.如果存在N维的正定矩阵P2以及适当维数的矩阵Q2使得下述线性矩阵不等式成立:

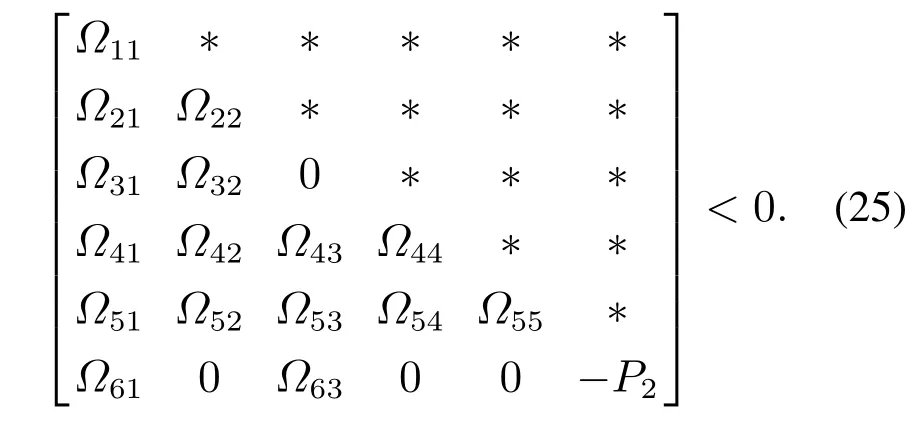
5 仿真与分析

采用文献[24]的多智能体拓扑结构,考虑由4个系统构成的网络系统,其拓扑结构如图1所示.

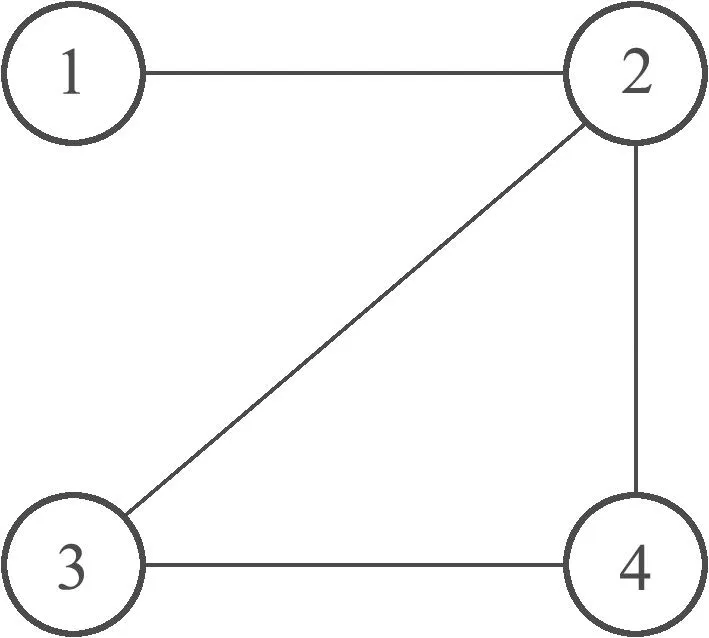
图1 拓扑结构Fig.1 Topological structure

每个系统各个系数矩阵如下:

控制输入u(k)为控制协议(18).未知输入ε(k)=0.8 cos(0.2k+2),非线性输入

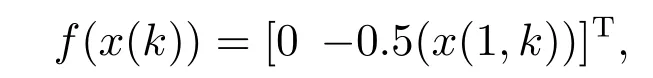
ξ(k)和η(k)均值为0,协方差矩阵同为

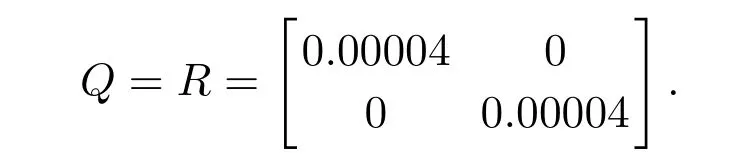
γ=0.55,τ=0.1.由上述参数求出

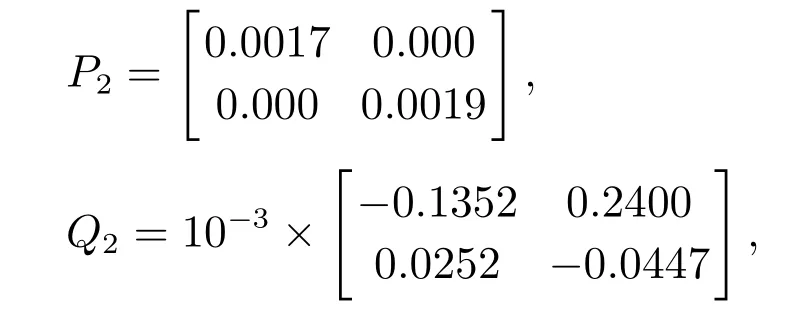
由此得到K=[-4.2817 7.5960].图2给出多智能体在无随机噪声情况下状态变化(Q=R=0),控制输入如图3所示,可以看到控制输入逐渐趋于0,并且各个系统最终收敛到一样的状态.

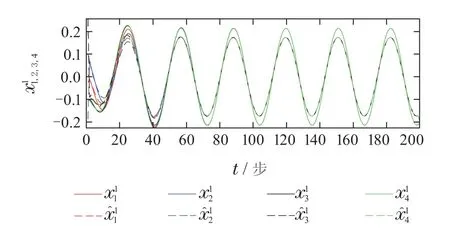
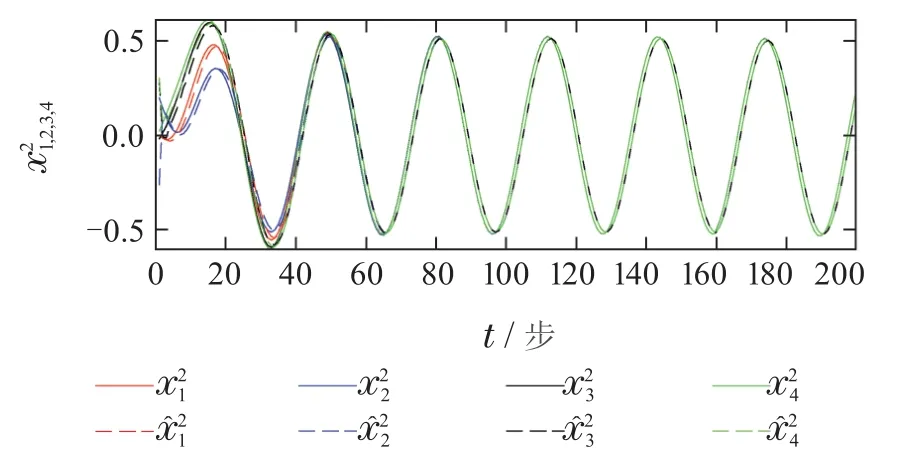
图2 本文算法中无随机噪声下系统状态及其估计Fig.2 System states and their estimations without random noise of algorithm in this paper

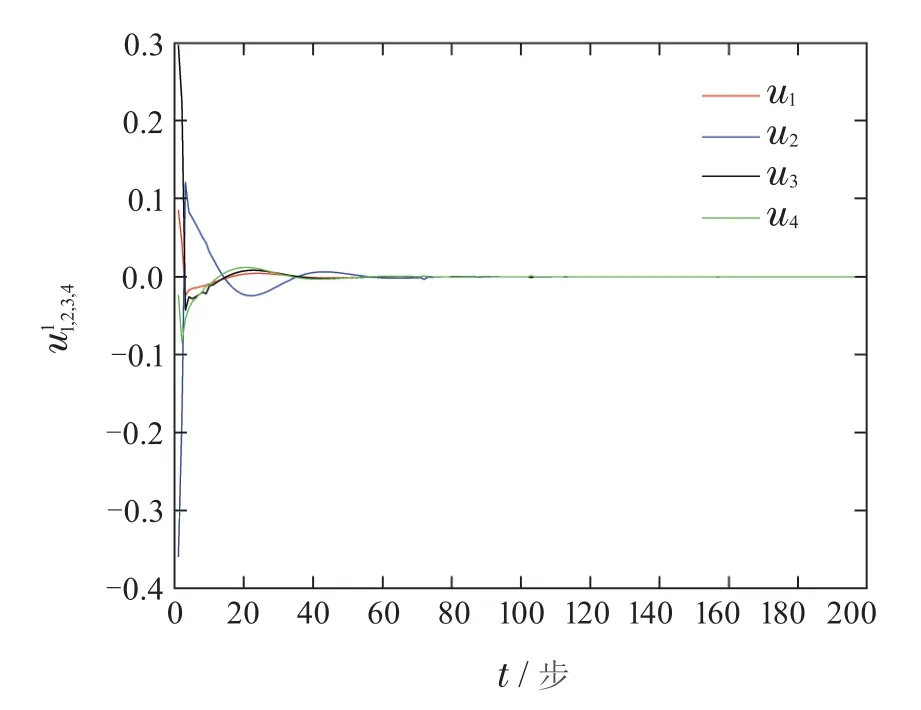
图3 本文算法中无随机噪声下控制输入Fig.3 Control inputs without random noise of algorithm in this paper

图4给出多智能体在随机噪声下状态变化情况,控制输入如图5所示.可以看到,从30步之后,控制输入逐渐趋于0,各个系统趋于一致,多智能体实现一致性控制.

图4 本文算法中随机噪声下系统状态及其估计Fig.4 System states and their estimations with random noise of algorithm in this paper

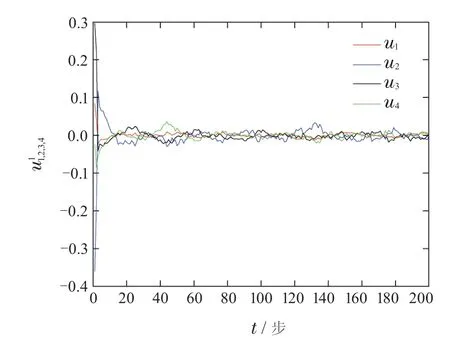
图5 本文算法中随机噪声下控制输入Fig.5 Control inputs with random noise of algorithm in this paper

图6给出文献[24]的方法中多智能体在没有随机噪声情况下状态变化情况,控制输入如图7所示,对比图2和图6、图3和图7可以发现文献[24]和本文的方法都可以使多智能体各个系统趋于一致,最终实现一致性控制.但是图3的控制输入明显比图7光滑,体现了本文方法的优势.

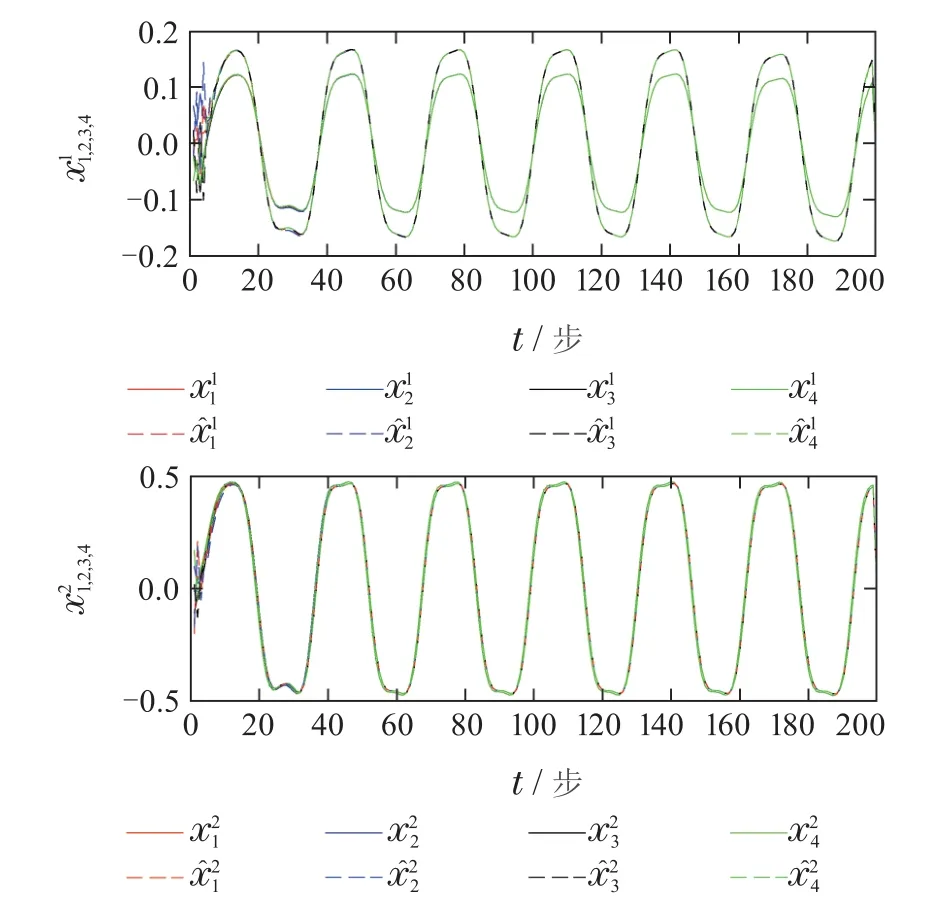
图6 文献[24]算法中无随机噪声下系统状态及其估计Fig.6 System states and their estimations without random noise of algorithm in literature [24]

图7 文献[24]算法中无随机噪声下控制输入Fig.7 Control inputs without random noise of algorithm in literature [24]

此外,图8-9给出文献[24]在含有随机噪声的情况下的结果.可以看出,在含有随机噪声的情况下,本文方法得到的结果明显较好.

图8 文献[24]算法中随机噪声下系统状态及其估计Fig.8 System states and their estimations with random noise of algorithm in literature [24]

图9 文献[24]算法中随机噪声下控制输入Fig.9 Control inputs with random noise of algorithm in literature [24]

6 结论

实际工业生产中,仪器的精密度会因磨损而老化,发生不可知的变化,从而产生未知输入.配件的老化同样会导致随机噪声的产生.文献[25]便是对此类问题的研究.多数论文仅针对一个问题来进行分析解决,考虑实际工业生产中未知输入与随机噪声可能会同时存在的情况下,本文通过数学推理证明将卡尔曼滤波器和未知输入系统结合所设计观测器能更好的抑制噪声.并且将其设计成多智能体的观测器.然后针对对非线性多智能体系统,提出了一种基于观测器的一致性控制协议设计方法.通过LMI求解增益矩阵,在有未知输入与随机噪声的干扰下实现多智能体的一致性控制.仿真结果表明,在面对同时含有随机噪声与未知输入的多智能体系统中,本文的方法效果显著,能够进行很好的多智能体一致性控制.未来将研究能否在扩展卡尔曼滤波器中以数据融合的方式解决带有随机噪声与未知输入的多智能体系统一致性控制问题以及如文献[26]所述通过一致性控制来进行多智能体的故障检测.