变截面波形钢腹板连续组合箱梁的剪切性能试验研究

赵 品，刘 鑫，荣学亮,2,3，陈 伟，张会斌

(1. 石家庄铁道大学 土木工程学院,河北 石家庄 050043；2. 交通工程结构力学行为与系统安全国家重点实验室, 河北 石家庄 050043;3.道路与铁道工程安全保障省部共建教育部重点实验室, 河北 石家庄 050043)

0 引言

波形钢腹板组合箱梁充分利用了混凝土抗压，波形钢腹板抗剪的特点，减轻自重、节约材料，解决了混凝土腹板开裂问题，是一种高效经济的桥梁结构。近些年来，波形钢腹板组合箱梁在国内发展快速，先后在河北、河南等省份建立了一大批波形钢腹板箱梁桥，如拔河大桥，新密溱水路桥，曾宇川桥等。随着该桥型在我国的大力推广，该桥型的计算理论也需要进一步完善。国内外学者对这种桥型进行了大量的试验，较为全面的掌握了该类桥型的剪切性能[1-6]。李立峰、侯立超等[7-8]进行了单箱三室波形钢腹板箱梁试验研究，得出了该桥型腹板剪力分配的特点。周绪红等[9]和聂建国等[10]通过试验对比，分别给出了考虑局部屈曲强度的半经验半理论式。宋建永等[11]对多片波形钢腹板箱梁进行了试验，验证了非线性计算程序是适用的。李杰等[12]利用有限元软件建立精细模型对波形钢腹板变截面连续体系梁桥钢腹板弯曲抗剪进行详细分析。刘宝东等[13]对波形钢腹板连续梁进行了抗弯试验研究，对连续梁的破坏过程进行了分析。

但是以上研究大多数针对简支梁,对于变截面连续梁而言,国内研究还比较少，并未对连续梁断面剪应力分布规律进行研究,也并未研究连续梁腹板剪切变形对挠度的影响。

本研究笔者在前任研究的基础上，进行了变截面波形钢腹板连续梁试验，对变截面波形钢腹板连续箱梁的抗剪性能进行研究，以期为波形钢腹板连续组合箱梁的试验研究和工程应用提供参考。

1 实验概况

1.1 梁体构造

试验梁为单箱双室波形钢腹板变截面面组合箱梁，跨径为(250+488+250)cm，中支座梁高710 cm，边支座梁高510 cm，中跨跨中梁高510 cm。中支座处腹板高度为50 cm，跨中及边支座腹板高度为30 cm。梁底线形为二次抛物线。箱梁顶板宽度为150 cm，底板宽度为108 cm。波形钢腹板与顶底板连接采用插入式方法。设置中跨2道横隔板，分别在中跨1/3位置，两边边跨跨中各设置1道横隔板，上述横隔板厚度均为10 cm。两边支座端分别设置一道横隔板，厚度为20 cm，两中支座位置分别设置1 m 宽的混凝土块。具体尺寸如图1所示。

图1 试验梁模型构造(单位：mm)Fig.1 Structure of experimental girder model (unit: mm)

混凝土材料为C40，波形钢腹板厚度为4 mm，波折角为37°，采用q235型钢材，具体尺寸见图2。试验梁采用体内、体外束混合配置，采用后张法张拉，预应力钢束为6束7根公称直径为14 mm的钢绞线，抗拉强度为1 860 MPa。

图2 波形钢腹板构造(单位：mm)Fig.2 Structure of corrugated steel web(unit: mm)

1.2 应变位移测点布置

在试验梁上一共布置了9个断面的钢腹板应变片，分别为2个边支座断面，2个中支座断面，2个边跨跨中断面，2个中跨1/4断面和1个中跨跨中断面。每个断面两侧钢腹板均贴3个45°直角应变花。在中跨跨中、中跨1/4、边跨跨中梁底位置沿横向布置3个精度为0.01 mm的位移计。具体布置如图3所示。由于应变测点与位移测点较多，所以采用WKD无线、总线多功能静态测试系统进行数据采集。为减小温度对试验的影响,波形钢腹板应变片接入温度补偿。

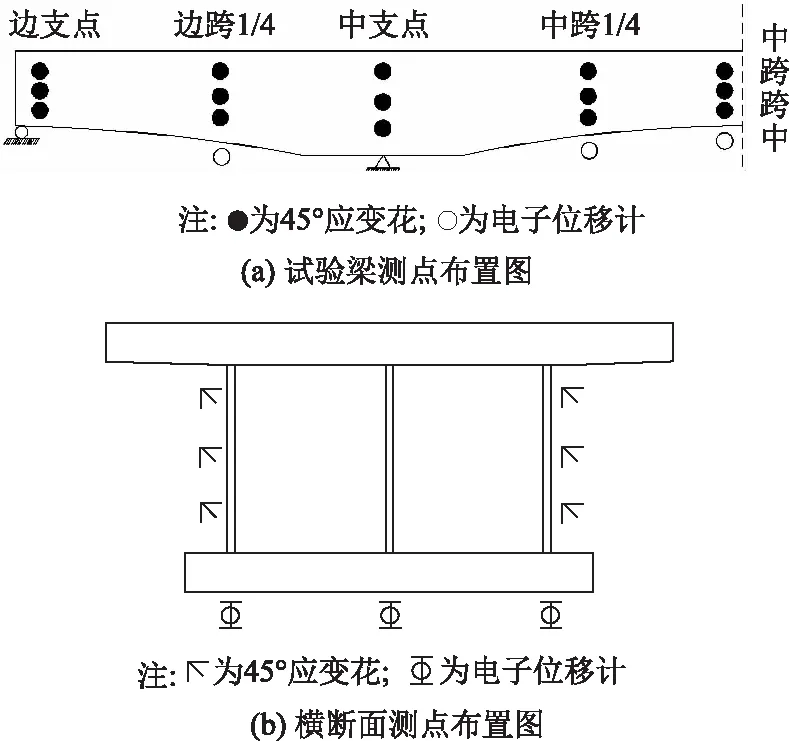
图3 测点布置图Fig.3 Layout of measuring points

1.3 加载方案

通过反力架和油压千斤顶对试验梁进行加载，荷载等级为60，120，180，240和300 kN，试验梁处于弹性阶段。为了防止加载过程中试验梁边跨向上位移，采用分配梁和钢绞线对边支座顶部进行固定，并使用油压千斤顶对钢绞线进行张拉，以消除钢绞线弹性形变的影响。加载前对试验梁进行预加载，荷载大小为60 kN，以消除各个部件之间空隙对试验精确度的影响。试验加载工况分为3个工况,中跨对称加载工况(工况Ⅰ),中跨三分点偏载工况(工况Ⅱ)，边跨单点加载工况(工况Ⅲ)。加载点具体位置如图4所示。边跨单点加载时由于受场地限制，油压千斤顶和反力架无法直接对边跨进行加载，所以通过钢绞线和分配梁自制了一个反力架，将钢绞线下端通过锚头固定在地板上，上端通过锚头固定在分配梁上，并对钢绞线进行预应力张拉。使用手动千斤顶手动进行加载，并在手动千斤顶底部放置压力传感器，用来测量荷载的大小。

图4 加载工况(单位:cm)Fig.4 Layouts of loading conditions (unit: cm)

2 波形钢腹板的剪应力

在波形钢腹板贴上45°应变花，实测剪应力值按照公式(1)计算[12]

τ=-G[2ε45°-(ε0°+ε90°)],

(1)

式中，τ为实测剪应力值；G为波形钢胶板剪切模量；ε0°为腹板纵向的应变值，ε45°为与腹板纵向夹角45°应变值，ε90°为腹板沿高度方向的应变值。

G=aGs=-68.4 GPa,

(2)

(3)

(4)

式中，G为波形钢腹板的剪切模量；Gs为钢材的剪切模量；μ为钢材的泊松比；E为钢材弹性模量；α为剪切刚度修正系数；其中b，c，d分别为波形钢腹板平板、斜板投影与斜板长度。

2.1 中跨加载波形钢腹板的剪应力

根据式(1)计算中跨对称加载，偏载作用下中支座断面与中跨1/4断面上3个测点的剪应力值如图5。

根据图5(a)和图5(b)，在中跨对称加载和中跨三分点偏载两种加载作用下，中跨1/4断面的剪应力值均随着荷载的增加而增大，并且沿梁高方向均匀分布。

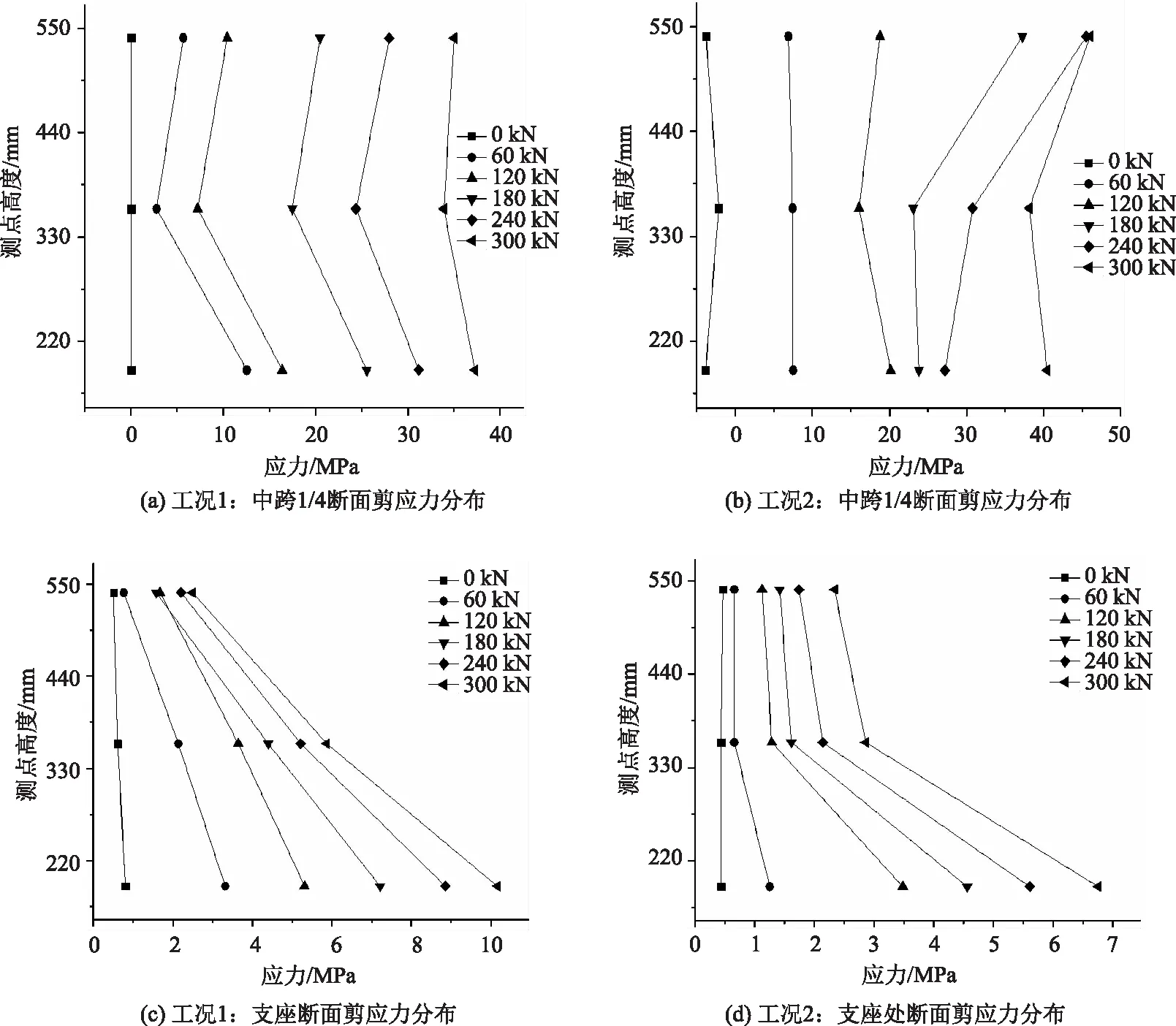
图5 不同断面处腹板剪应力分布Fig.5 Distribution of shear stresses at different cross-sections

由图5(c) 、图5(d)可知，相同荷载作用下，中支座断面波形钢腹板的剪应力值沿着梁高方向变小；靠近底板位置的剪应力值最大，其次为腹板中间位置，靠近顶板位置的腹板剪应力值最小。随着荷载的不断增加，支座断面的剪应力值也逐渐增大，并且靠近底板位置的剪应力值的增长速度远远大于其他高度位置的增长速度，说明梁底承受更大的剪力。在设计时，应对该位置的抗剪能力进行考虑。

变截面连续梁不同断面腹板所承担的剪应力不同，根据试验可得中跨对称加载时不同断面的荷载-剪应力值曲线如图6所示。

图6 工况1：腹板剪应力-荷载曲线Fig.6 Case 1: curves of shear stress vs. load of web

中跨1/4断面和边跨跨中断面波形钢腹板剪应力的绝对值随着荷载的增大而增大，并且中跨1/4断面剪应力的绝对值大于边跨跨中断面；剪应力-荷载曲线近似为线性曲线，这说明波形钢腹板未达到其屈服强度，且各断面剪应力值体现了连续梁的受力特点。

随着荷载的增加，跨中1/4处的剪应力值随着荷载的增大而显著增大，而中支座处的剪应力增长较为缓慢，中跨跨中和中支座位置的剪应力值很小。在整个试验中，各个断面荷载-应力曲线较为平滑，没有出现突变现象。

2.2 边跨加载腹板剪应力

利用式(3)计算对边跨加载时波形钢腹板剪应力值，计算结果如图7所示。

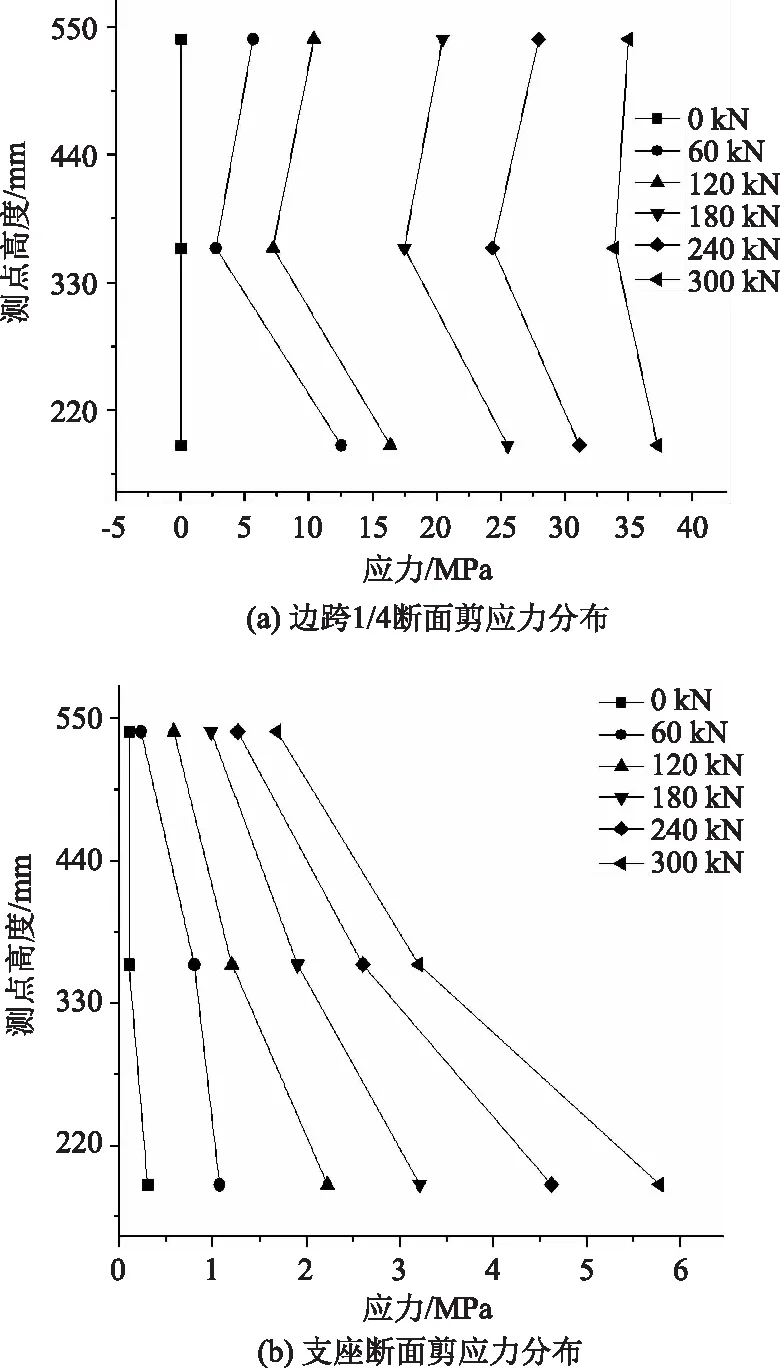
图7 断面剪应力分布Fig.7 Distribution of shear stresses at cross-section

由图7(a)可知，在对试验梁边跨加载时，边跨1/4断面的剪应力值沿梁高方向均匀分布，并且随着荷载的增大而增大；在支座断面，靠近底板的剪应力值略大于沿梁高方向的其他值。边跨1/4断面剪应力变化规律与中跨加载时中跨1/4断面的剪应力变化规律基本一致。为了探究中跨加载与边跨加载对中支座的影响，对两种工况下中支座处波形钢腹板剪应力值进行对比。由图8可知，在相同荷载下，试验梁在边跨跨中加载时，中支座断面的剪应力值小于中跨对称加载时中支座截面的相应值。故与中跨对称加载时相比，边跨加载时对中支座处剪应力值的影响较小。故在实际应用中，应该着重考虑对连续梁中跨加载对中支座的影响。

图8 支座断面剪应力对比Fig.8 Comparison of shear stresses in bearing section

2.3 波形钢腹板附加剪应力

试验梁在承受偏心荷载时，波形刚腹板的受力与对称加载相比会有明显不同，距离加载位置较近的腹板承受的剪力会增加，距离加载位置较远的腹板承受剪力会减小。若在对称荷载作用下波纹钢腹板剪应力为τM, 相应偏心荷载作用下的波纹钢腹板剪应力为τE，波形钢腹板附加剪应力为[14-16]。

Δτ=τE-τM。

(5)

对两种工况下波形钢腹板的剪应力值进行对比如图9所示。

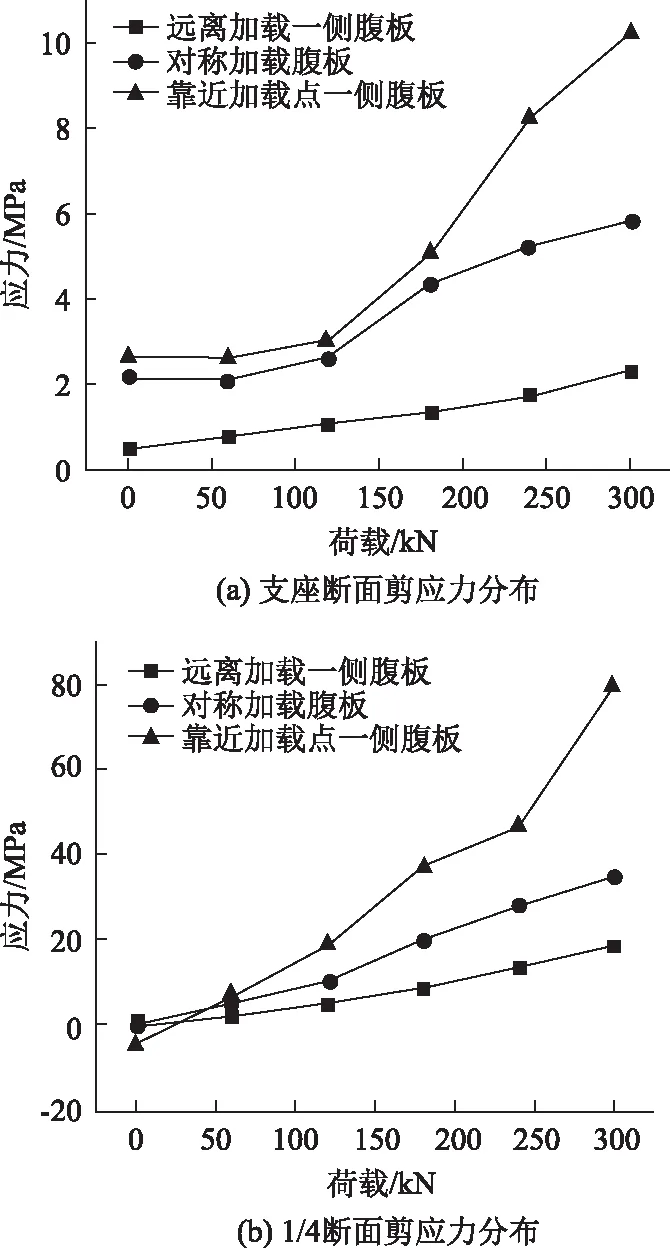
图9 断面剪应力分布Fig.9 Distribution of shear stresses at cross-section

根据图9(a)，试验梁支座断面的剪应力值随着荷载的增加而增加，在对试验梁中跨对称加载时，波形钢腹板剪应力的值位于在偏载作用下，距离加载位置较近腹板的剪应力值与距离加载位置较远腹板的剪应力值之间。在荷载小于120 kN时，波形钢腹板的剪应力值增长速度较为缓慢，大于120 kN时，波形钢腹板的剪应力值增长速度加快。

根据图9(b)，当试验梁中跨承受偏载时，中跨1/4断面靠近加载点一侧波形钢腹板的剪应力值增长速度明显大于远离加载点一侧波形钢腹板的剪应力值与对称加载波形钢腹板的剪应力值。由表1可知，当荷载增大时，中跨1/4断面的附加剪应力值也随之增加，与等截面梁相比，变截面连续梁附加剪应力的影响更为显著：当荷载为300 kN时，附加剪应力值达到了弯曲剪应力值的120%；说明波形钢腹板连续梁承受的荷载越大，偏载作用下箱梁的扭转对波形钢腹板剪应力值的影响越大。

表1 中跨1/4断面附加剪应力Tab 1 Additional shear stress in middle span 1/4 section

3 试验梁的挠度

试验梁在对称加载工况下，中跨跨中和中跨1/4断面处的挠度如图10所示，荷载-位移曲线呈现线性规律，证明试验梁处于弹性阶段。当忽略波形钢腹板对试验梁挠度的作用时，假设试验梁仅由顶板，底板组成，由虚位移原理可得，计算试验梁中跨1/4断面在对称加载下处的挠度：

(6)

式中,y1为由弯矩引起挠度；M(x)为断面弯矩；P为两点对称荷载；l为试验梁计算跨径；E=2.45×10-4MPa为混凝土弹性模量；Ic=1.704×10-2m4为忽略钢腹板的断面惯性矩。

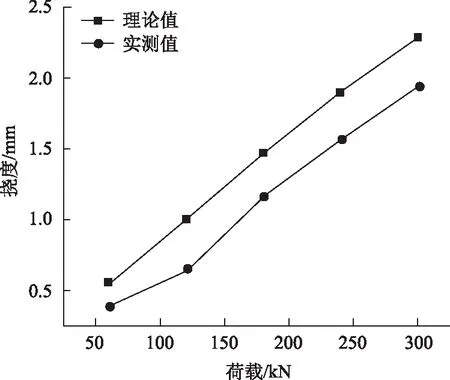
图10 偏载下试验梁中跨1/4断面荷载-挠度曲线Fig.10 Curves of Load vs. deflection at 1/4 section of middle span test girder under partial load

按照式(6)对试验梁的理论挠度进行计算，对比试验梁中跨1/4断面在不同荷载下理论挠度值与试验挠度值，其中试验挠度值为在对称加载下，中跨1/4断面底板处3个位移计的平均值。由图10可知, 试验梁理论挠度值与试验挠度值吻合较好, 且理论计算值偏安全。由此可知，当对变截面连续梁中跨施加对称荷载时，试验梁挠度受钢腹板剪切变形的影响较小。

在对中跨三分点施加偏心荷载时,试验梁靠近加载点一侧实测挠度大于对称加载时的实测挠度。随着试验荷载增加，挠度也不断增大，但其增加幅度占对称荷载下的挠度的比例越来越小。由表2可见,当试验梁处于弹性阶段时，随着荷载的增加，波形钢腹板的剪切变形对挠度影响越来越小。

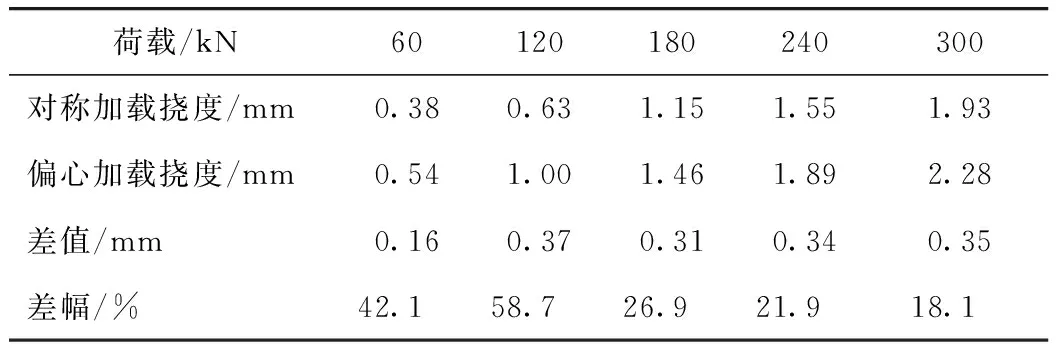
表2 试验荷载作用下挠度值的对比Tab.2 Comparison of deflection values under test load

如图11所示，当偏心荷载作用在试验上时，靠近加载点一侧实测挠度明显大于对称加载实测挠度，这种现象说明在偏载作用下，波形钢腹板发生了剪切变形，且对挠度的影响不能忽视[17-19]。

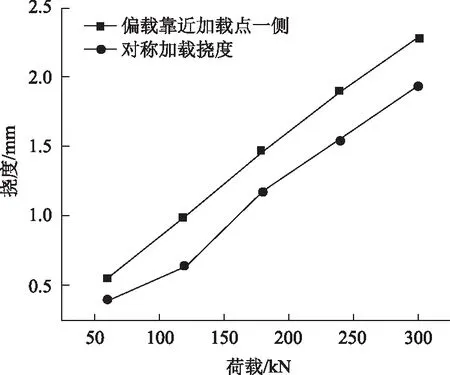
图11 试验挠度值的对比Fig.11 Comparison of deflection values in test

设由波形钢腹板剪切变形影响的挠度为y1，该挠度并不引起梁的纵向位移，当剪力单独作用时，梁挠度曲线上任意一点的斜率等于该处的剪应变，即

(7)

式中，Q(x)为断面剪力；A波形钢腹板抗剪断面面积A=2ht；h为波形钢腹板断面高度；t为波形钢腹板断面厚度；K为应力非均匀系数,因断面不同取不同值[18]，对于波形钢腹板箱梁，剪力大部分由波形钢腹板承担的，并且剪应力沿梁高方向均匀分布，所以取应力非均匀系数K=1.0，则

(8)

(9)

式中,y2为波形钢腹板剪切变形影响下的挠度，对y2取偏微分为dy2；dx为微元体的宽度；G为剪切模量，G=a·Gs=-68.4 GPa；总挠度为弯矩引起的挠度加上剪力引起的挠度，即y=y1+y2,得到：

(10)

解此微分方程即可得到在考虑剪切变形时梁的总挠度y，对于波形钢腹板连续梁，所承受的剪力跟弯矩与简支梁有很大不同，在两点对称加载情况下，如图12所示，

图12 两点加载下的连续梁示意图Fig.12 Schematic diagram of continuous girder under 2-point loading

对于中跨断面而言，剪力如下：

(11)

当x=0，y2=0，有C1=0，由上式等于

(12)

在连续梁中跨跨中1/4断面处

(13)

即在中跨跨中1/4断面总的挠度为

(14)

利用式(14)计算得到各级试验荷载作用下试验梁的挠度值与试验值进行对比，如图13所示，试验值与理论值吻合较好，理论值略大于实测值，误差在8%以内。

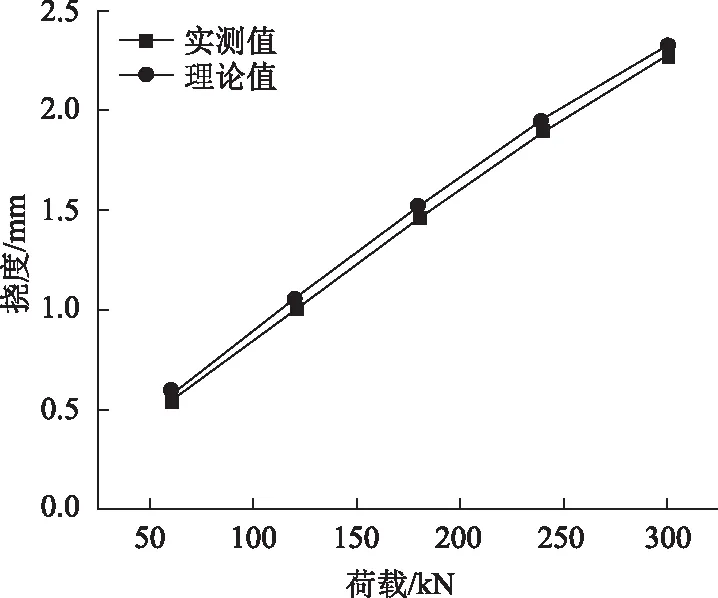
图13 中跨1/4荷载挠度曲线Fig.13 Curves of load vs. deflection at 1/4 section of middle span

4 结论

(1)在中跨对称加载时，中跨1/4处剪应力沿梁高均匀分布，并且随着荷载的增加呈线性变化，整个对称加载过程试验梁处于弹性阶段；支座处靠近底板位置的腹板剪应力值略大于该断面腹板其他高度位置的相应值，在设计时，应对该位置的抗剪能力进行考虑。

(2)边跨加载时，中跨1/4断面的剪应力变化规律与中跨加载时变化规律基本一致。在相同荷载作用下，边跨加载时中支座处断面的剪应力值小于中跨加载时的相应值，这说明了连续梁边跨承受荷载时，对中支座位置的剪应力影响较小。

(3)在中跨三分点偏载作用下，靠近加载点一侧的剪应力值大于远离加载点一侧的剪应力值；荷载大于120 kN时，中跨1/4断面波形钢腹板的剪应力值增长速度较快。与等截面梁相比，变截面连续梁附加剪应力的影响更为显著，当荷载为300 kN时，附加剪应力值可达到弯曲剪应力值的120%，可见当荷载越来越大时，试验梁的扭转对钢腹板的剪应力影响也越来越大。

(4)在弹性范围内对试验梁施加对称荷载时，试验梁挠度受钢腹板剪切变形的影响较小。中跨三分点偏载作用时，其1/4断面靠近加载点一侧的挠度相比对称加载时有明显的增大，其增加幅度占对称荷载挠度的比例越来越小，这说明了试验梁中钢腹板的剪切变形对挠度影响越来越小。推导出了波形钢腹板连续梁在考虑剪切变形时的挠度计算公式，公式计算值与试验值的误差在8%以内，吻合较好。