基于ANFIS-PID控制策略的主动悬架动力学性能研究

辛 亮，杜子学，许舟洲

（1.重庆交通大学轨道交通研究院，重庆400074；2.重庆交通大学机电与车辆工程学院，重庆400074）

1 引言

传统的被动悬架由于其固定的刚度和阻尼，只能在特定的路况下达到最优的状态［1］。而主动悬架突破了传统被动悬架的局限性，能根据不同的路况进行主动控制，极大地改善了车辆的动力学性能［2］。主动悬架主要包括控制策略和作动器两部分，其中控制策略是主动悬架的核心［3-4］。目前，主动悬架的控制策略主要有：PID控制［5］、LQG控制［6］、天棚控制［7］、模糊控制［8-9］和神经网络控制［10］等。由于PID控制具有结构简单和易于实现等优点，从而在工程中得到广泛的应用。但是PID控制依赖于精准的数学模型，对于存在大干扰、高度非线性和不确定性的复杂系统，难以达到预期的控制效果［11］。

模糊控制和神经网络控制是智能控制的两大关键技术，都不依赖于对象的数学模型，是处理非线性和不确定性的有力工具［12-13］。因此，在1/4车辆主动悬架模型的基础上，我们将模糊控制、神经网络控制和PID控制进行有机结合，设计了主动悬架的ANFIS-PID控制策略，并与传统的PID控制进行了对比，以期主动悬架系统的研究提供新的思路。

2 主动悬架动力学模型

我们将悬架系统简化为线性的弹簧单元和阻尼单元，轮胎简化为线性的无阻尼弹簧单元，建立1/4车辆的主动悬架动力学模型进行研究，如图1所示。

图1 1/4主动悬架动力学模型Fig.1 1/4 Dynamic Model of Active Suspension

根据牛顿运动定律，可得主动悬架的运动微分方程为：

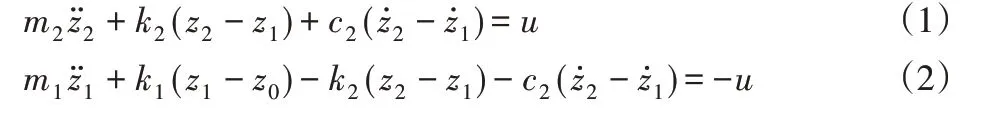
式中：m2—车身质量；m1—轮胎质量；k2—悬架刚度；k1—轮胎刚度；c2—悬架阻尼系数；z2，z1和z0—车身位移、轮胎位移和路面不平度的位移输入；z2—车身加速度，k1(z1-z0)轮胎动载荷；u—作动器，用于输出主动力。

采用滤波白噪声作为路面输入模型，即：

式中：G0—路面不平度系数；ω—均值等于0的高斯白噪声；f0—下截至频率；v—车速。

悬架系统各参数取值，如表1所示。

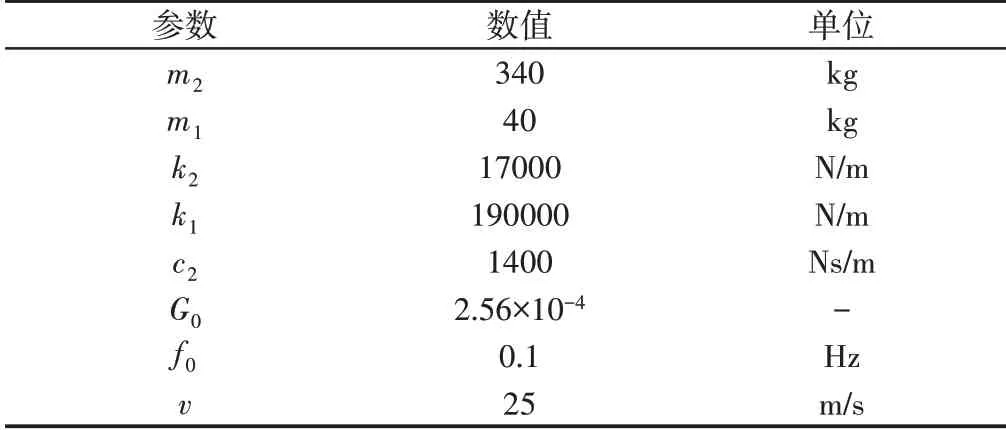
表1 悬架系统参数Tab.1 Parameters of Suspension System

3 ANFIS-PID控制策略

传统PID的控制参数一般是通过经验试凑出来的，一经固定便无法根据系统的状态实时调整，系统很难达到最佳的控制效果。我们采用一种自适应模糊推理系统整定PID的方法，实现对PID参数的实时调整，从而保证系统一直处于最优的状态。

3.1 ANFIS原理

自适应模糊推理系统（ANFIS）是基于Takagi-Sugeno模型的模糊推理系统［14］，该系统将神经网络与模糊推理系统相结合。该算法根据输入输出对的信息，自动生成if-then规则，实现隶属函数的在线调整。

ANFIS结构有5层，其典型结构，如图2所示。结构的输入是误差及其变化率。第一层是隶属度函数生成层。该层中的每个神经元节点代表一个逻辑语言值。隶属函数为高斯函数：

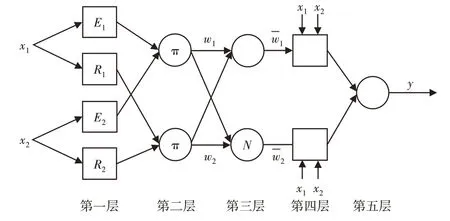
图2 ANFIS典型结构图Fig.2 Typical Structure of ANFIS

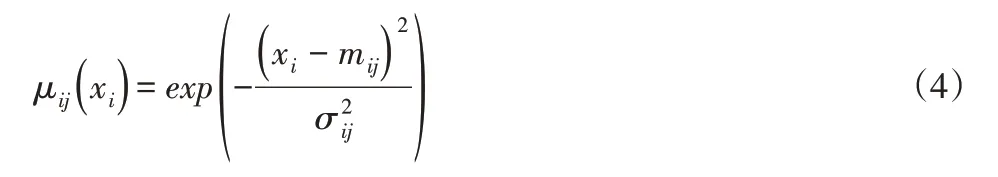
式中：i—输入变量的数量；j—模糊变量的个数；μij(xi)—输入变量对应的模糊变量值；mij—高斯函数的中心值；σij—高斯函数的宽度。

第二层是模糊推理层，每个节点代表一个模糊规则，通过隶属度函数相乘得到每个规则的触发强度通过：

第三层决定了每个规则的触发强度与所有规则的触发强度之和的比率。输出是归一化后每个规则的触发强度。

第四层给出每个规则的输出：

式中：fk—输出变量的隶属函数，pk，qk和rk系数。

第五层是解模糊层，它计算系统的总输出。

3.2 ANFIS-PID控制方法

我们提出的ANFIS-PID控制方法是将传统的PID控制、模糊控制与神经网络控制相结合，实现对PID参数的实时调整，从而保证系统一直处于最优的状态。ANFIS-PID的结构图，如图3所示。对于主动悬架系统，控制回路将采集到的车身速度值和设定的车身速度值偏差e和速度偏差变化率（即车身的加速度偏差）de/dt输入到模糊推理中，然后经过ANFIS结构的最小二乘法和神经网络模块自适应输出Δkp，Δki，Δkd，从而实现PID参数的在线调整。

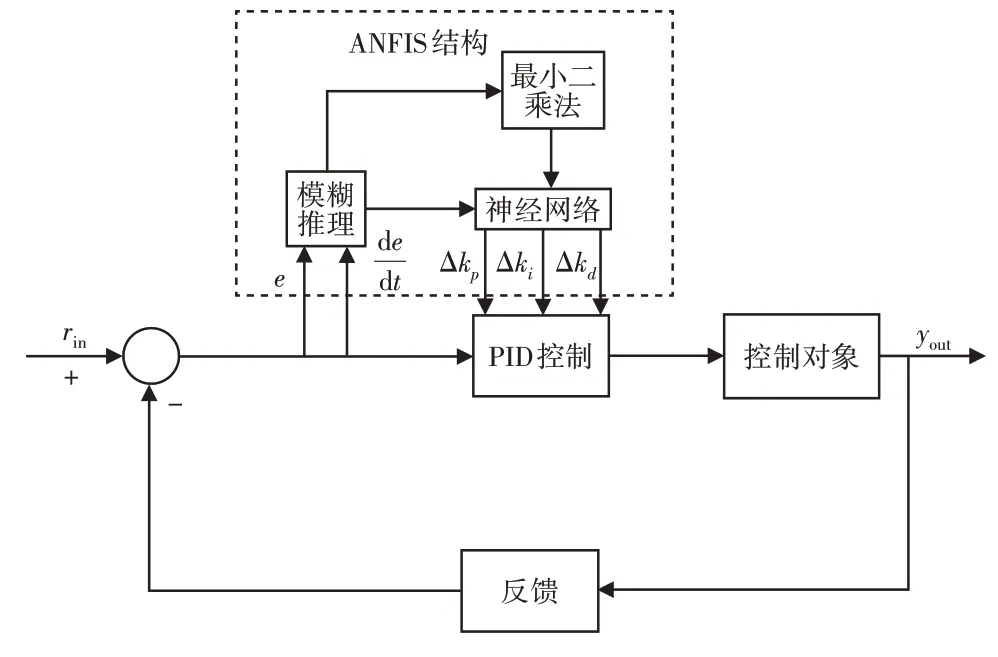
图3 ANFIS-PID结构图Fig.3 ANFIS-PID Structure Diagram

4 仿真结果

为了验证提出的ANFIS-PID 控制策略的控制性能，将AN⁃FIS-PID控制结果与传统的PID控制结果进行对比。设置仿真时间为10s，PID控制主动悬架和ANFIS-PID控制主动悬架的车身加速度和轮胎动载荷的时域对比，如图4所示。由图4可知，AN⁃FIS-PID 控制策略下的车身加速度和轮胎动载荷均低于传统的PID控制策略。为了进一步说明ANFIS-PID控制策略的控制效果，车辆的车身加速度和轮胎动载荷的均方根值（RMS）对比，如表2所示。从表2中可以看出，相比于传统的PID控制策略，AN⁃FIS-PID控制策略的车身加速度均方根值降低了22.96%，轮胎动载荷均方根值降低了32.67%。由此可见，相比于PID控制策略，ANFIS-PID控制策略能进一步减小车辆的振动，可有效提高车辆的行驶平顺性。

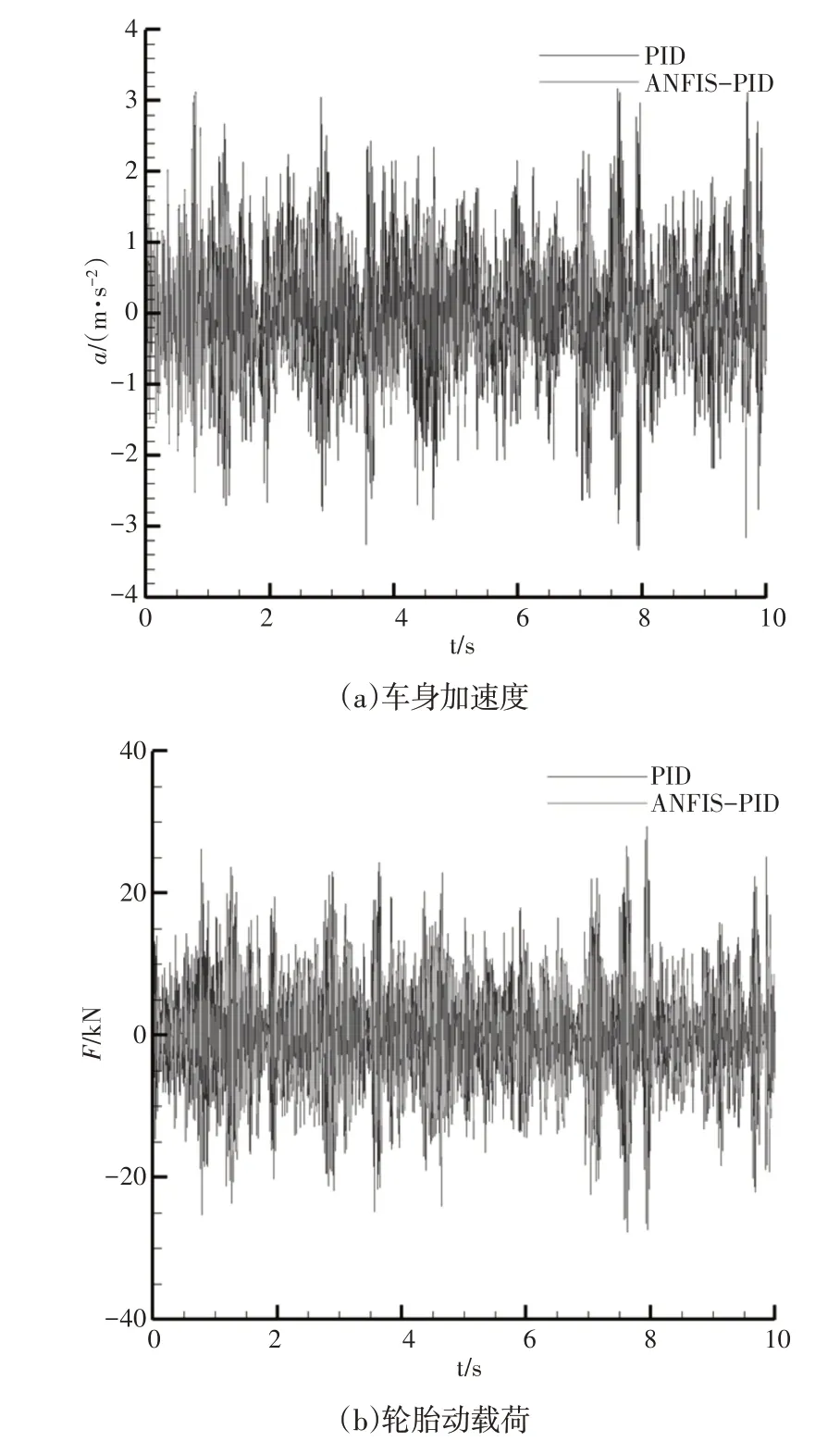
图4 动力学性能时域对比Fig.4 Comparison of Dynamic Performance

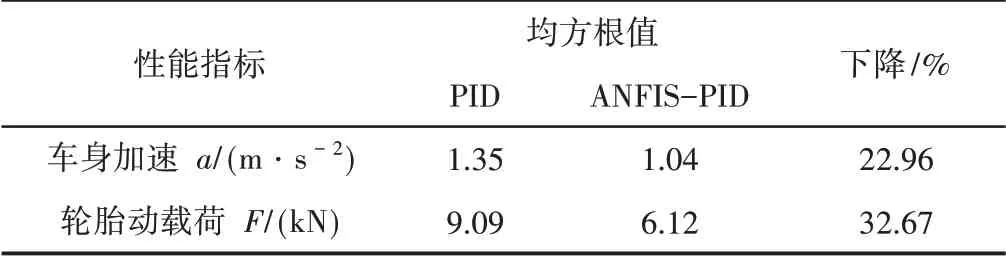
表2 均方根值对比Tab.2 Comparison of Root Mean Square Values

5 结论

在1/4 车辆主动悬架动力学模型的基础上，我们将传统的PID控制、模糊控制与神经网络控制相结合，设计了ANFIS-PID控制策略，对车辆的垂向运动进行了控制。仿真结果表明，相比于传统的PID控制策略，ANFIS-PID控制策略的车身加速度均方根值降低了22.96%，轮胎动载荷均方根值降低了32.67%。所提出的ANFIS-PID控制策略具有较好的应用价值。