齿轮五杆机构齿轮链的研究

王 君，陶 芬，姜荣俊，汪 泉

（湖北工业大学机械工程学院机器人技术研究中心，湖北 武汉 430068）

1 引言

齿轮五杆机构结构简单，是种类最多、应用最广的一种组合机构，它由定传动比的齿轮机构与变传动比的连杆机构组合而成，可实现较复杂的运动规律和轨迹，改变齿轮传动比即可调整从动杆的运动规律或轨迹［2］。因此，研究齿轮链对机构运动规律的影响具有非常重要的理论意义及价值。

齿轮链包括传动比及初相角两个参数，许多文献［1-5］通过改变其中一个参数，讨论了齿轮五杆机构的传动比和相位角分别对机构轨迹曲线的影响，这种方法得到的结果具有局限性。考虑到齿轮链两个参数同时改变对机构轨迹曲线的影响，先研究只改变一个参数时，机构轨迹曲线的变化规律，再结合两个参数同时变化时机构轨迹曲线的变化规律，进行对比，可得出传动比和初相角对机构轨迹曲线的影响规律。在机构设计、综合及应用中，机构的可动性识别不仅能帮助机构进行连续平滑的运动，避免运动缺陷，还能帮助提高机械产品设计的效率和经济性［7］。机构可动性［8］有三个主要问题，即分支，子分支和完全旋转性。运动缺陷指的是两个分支之间，机构不能通过连续运动所达到的位置［7］。运用判别法［8］来分析齿轮五杆机构的可动性，识别了机构的分支、子分支及完全旋转性，分析了齿轮链中的传动比和初相角参数对机构可动性［8］的影响，提出了在机构设计和综合过程中将无分支点作为完全旋转性约束条件，来避免运动缺陷和运动不连续。针对不具有完全旋转性的齿轮五杆机构，提出通过改变传动比及初相角的值来纠正分支。

2 齿轮链与轨迹曲线研究

2.1 齿轮五杆机构的数学模型

齿轮五杆机构，设连杆长度为a（ii=1..5），杆件对应的角度为θ（ii=1..5），a1为机架，主动齿轮2和从动齿轮5分别固接于五杆机构的曲柄AB和曲柄DE上，约束了五杆机构的1个自由度，组合成了单自由度齿轮五杆机构，如图1所示。各杆与x轴正方向的夹角以逆时针方向为正。

图1 齿轮五杆机构Fig.1 Geared Five-Bar Linkage

齿轮约束一般为：θ2-θ20=n(θ5-θ50)

式中：θ20、θ50—曲柄2和曲柄5的初相角；n—齿轮传动比。

当θ20=0，θ50=α时，齿轮约束可表示为：

五杆机构的环方程为：

将式（2）向x和y方向投影得到位移方程：

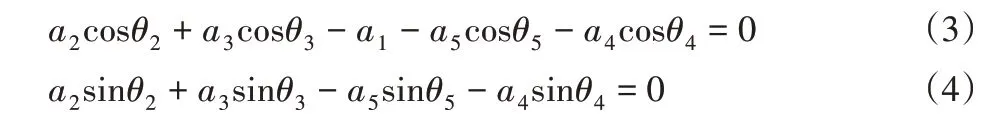
各杆尺寸一定，当输入杆a2旋转到某个角度θ2时，输出杆转角θ5可通过齿轮约束（1）求解，而连杆a3、a4的转角θ3、θ4可根据矢量式（3）、式（4）求解，这是解析法的基本思路。

但解析法计算过程繁琐且不直观，而利用Matlab中的fsolve函数可以很方便地求解，fsolve函数相当于对矢量方程等式左边就目标值0寻优求值，表达式为［6］：

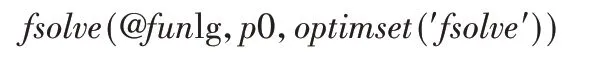
当输入杆a2以一定的规律运动时，C点的坐标值（xC，yC）受到输入杆尺寸a2及其转角θ2、连杆尺寸a3及其转角θ3的控制，其关系式为：

当a2、a3的值固定时，C点的坐标值（xC，yC）仅受输入角θ2、连杆转角θ3的影响，而θ3可由式（3）、式（4）联立求解获得，即C点坐标仅与θ2有关，每一个θ2值都对应了一个C点的坐标值，取k个θ2值可得到k个C点坐标，只要C点坐标足够多，即k足够大，Matlab就可将C点坐标拟合成一条轨迹曲线。

而θ2的取值则受齿轮链的约束，因此，C点的轨迹曲线受齿轮链的影响，而齿轮链中包含传动比及初相角参数。

考虑到齿轮链两个参数同时改变对机构轨迹曲线的影响，先研究只改变一个参数时，机构轨迹曲线的变化规律，再结合两个参数同时变化时机构轨迹曲线的变化规律，进行对比，可得出传动比和初相角对机构轨迹曲线的影响规律。

2.2 传动比对轨迹曲线的影响

取a1=80，a2=a5=30，a3=a4=70，两初相角θ20=θ50=0，当两齿轮转动方向相反时，改变齿轮传动比大小，取n=1，2，3，4，5，6整数。在传动比变化的过程中，C点轨迹曲线的形状由简单的8字形变为复杂的编织形状，并且传动比的数值越大，曲线的弯折次数越多，图形越复杂，如图2所示。

图2 传动比对轨迹曲线的影响Fig.2 Influence of Gear Ratio on Trajectory Curve

2.3 初相角对轨迹曲线的影响

取传动比为n=1，各杆长度保持不变，主动曲柄的初相角θ20=0，只改变从动曲柄的初相角α，C点的轨迹曲线的变化，如图3所示。α由0向π变化时，C点的轨迹曲线由水平8字形逐渐变化为竖直的直线形状［1］；并且在α=(0～π)和α=(π～2π)的变化过程中，轨迹变化关于α=π处的直线对称。

图3 n=1时初相角对轨迹曲线的影响Fig.3 Influence of Initial Phase Angle on Trajectory Curve when n=1

随着初相角的变化，C点的轨迹曲线发生了变化，并且变化是对称的，除此之外没有明显的变化规律。

2.4 传动比及初相角对轨迹曲线的影响规律

前文研究齿轮链中的单个参数对轨迹曲线的影响，可以看出，单个参数对C点轨迹曲线有影响，但却没有明显的规律。改变初相角的同时也改变传动比，对轨迹曲线的变化进行归纳：取传动比为2，各杆长度保持不变，主动曲柄的初相角θ20=0，只改变从动曲柄的初相角α，C点的轨迹曲线，如图4所示。取传动比为3，各杆长度保持不变，主动曲柄的初相角θ20=0，只改变从动曲柄的初相角α，C点的轨迹曲线，如图5所示。

图4 n=2时初相角对轨迹曲线的影响Fig.4 Influence of Initial Phase Angle on Trajectory Curve when n=2

图5 n=3时初相角对轨迹曲线的影响Fig.5 Influence of Initial Phase Angle on Trajectory Curve when n=3

对比图2与图3，当n=1时，C点轨迹曲线在α=0和α=2π时完全相同，说明α=(0～2π)为一个变化周期。

对比图2与图4，当n=2时，C点轨迹曲线在α=0和α=π、α=2π时完全相同，并且在α=π/3和α=4π/3时完全相同，说明α=(0～π)为一个最小变化周期。

对比图2 与图5，当n=3 时，C点的轨迹曲线在α=0 和α=2π/3、α=4π/3、α=2π 时完全相同，并且在α=π/3 和α=π、α=5π/3时完全相同，说明α=(0～2π/3)为一个最小变化周期。

由此总结出C点轨迹曲线的变化规律：当传动比为n时，初相角α=(0～2π/n)为C点轨迹变化的最小周期，即在同一传动比下，初相角相差2π/n的轨迹曲线完全相同。

3 齿轮五杆机构可动性分析

3.1 齿轮五杆机构的环路分析

齿轮五杆机构可视作一个二自由度五杆环与一个齿轮链相耦合，齿轮链约束了五杆环的一个自由度，使得二自由度五杆机构变成单自由度双环机构。对于单自由度多环的机构，每个环路都有其运动特性，整个机构必须同时满足每个环路的运动条件，才能进行装配和运动。二自由度五杆链的两个输入关节θ2和θ5之间的运动范围称为关节旋转空间［9］，通过五杆链的环方程来求解，而齿轮链的可行域则为输入关节θ2与输出关节θ5之间的输入输出曲线，即式（1）。

用三角平方关系sin2θ4+cos2θ4=1消去式（3）和式（4）中的θ4，式（2）可表示为：

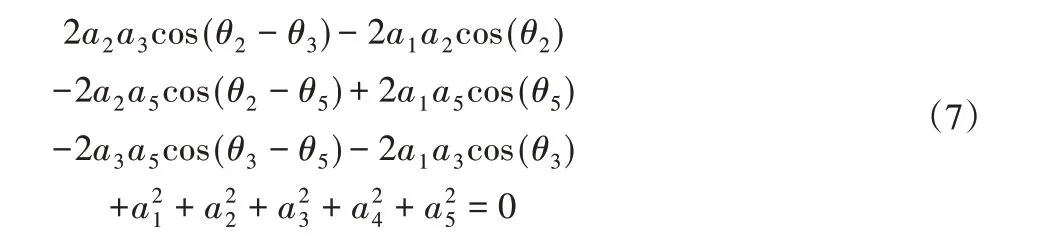
代入公式x3=tan(θ3/2)，式（7）可表示为：

式（8）是一个二次方程，当A1≠0时，五杆链能连续运动的条件为：

根据式（8）和式（9），每种机构构型可以唯一确定，其为：

x3和θ3之间是一一对应的关系，由式（10）或式（11）唯一确定。当Δ1=0时，式（8）只有一个解，五杆链处于奇异位置，一个输入对应一种机构构型；当Δ1>0时，式（8）有两个解式（10）、式（11），对应着五杆机构的两种构型；当Δ1<0时，式（8）无解，说明在此机构参数下，机构不能连续运动。因此，式（9）约束了五杆链的可行域。

将式（9）进行化简，可得到：

其中：

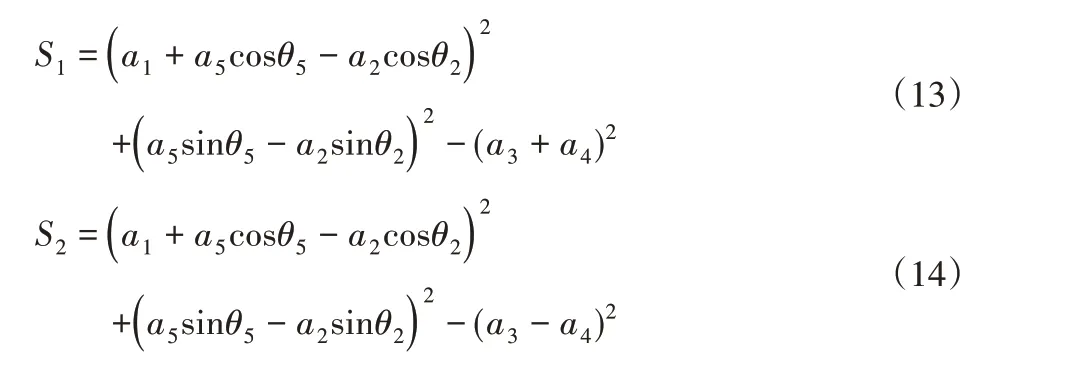
式（12）表示了五杆链中θ2和θ5之间的运动范围，即关节旋转空间，式（13）、式（14）中的S1=0和S2=0表示关节旋转空间的边界［9］，也可称为边界曲线或奇异曲线。边界曲线上的点表示五杆链处于奇异位置，此时二杆组BCD处于拉伸共线（S1=0）或重叠共线状态（S2=0），五杆链退化为四杆链，关节旋转空间内的点表示五杆链能运动到此位置。

3.2 齿轮五杆机构的分支点识别

机构只有一个自由度，说明只要确定输入值便可得到整个机构的可行性，但由于分支点的存在导致机构仅在某一段角度区间中具有可行性，且齿轮五杆机构的分支点位于齿轮链的特征曲线与五杆链的关节旋转空间边界的交点处。

将式（1）代入边界曲线S1消去θ5，并代入半角公式x2=tan(θ2/2)，可得到关于x2的一元二次方程：

当Δ2>0时，方程有两个不同解：

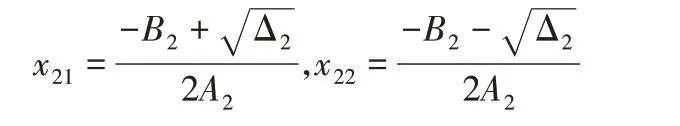
A2、B2、C2及Δ2是关于传动比n及初相角α的关系式。当Δ2>0时，式（15）有两个解，齿轮链的特征曲线与五杆链的边界曲线S1存在两个交点，机构分支点为θ21，22=2arctan(x21，22)；当Δ2=0时，式（15）只有一个解，机构只有一个分支点；当Δ2<0 时，式（15）无解，齿轮链的特征曲线与五杆链的边界曲线S1无交点，机构不存在分支点。

同理，将式（1）代入边界曲线S2消去θ5，并代入半角公式x2=tan(θ2/2)，可得到：

其判别式：Δ3=，当Δ3>0时，方程有两个不同解：

若Δ3>0，方程（16）有两个解，齿轮链的特征曲线与五杆链的边界曲线S2存在两个交点，机构分支点为θ23，24=2arctan(x23，24)；当Δ3=0 时，式（16）只有一个解，机构只有一个分支点；若Δ3<0，方程（16）无解，齿轮链的特征曲线与五杆链的边界曲线S2无交点，机构不存在分支点。

3.3 齿轮五杆机构分支及子分支识别

分支指的是一个连杆机构的所有构型空间，在这个构型空间中连杆机构可实现构型之间的连续转换［7］。子分支指的是一个连杆机构的连续的构型空间，在子分支内，机构可以完成构型之间的连续转换且不存在奇异点。对于齿轮五杆机构，必须同时满足齿轮链和五杆链的运动条件，才能连续运动。

可通过以下方法来识别齿轮五杆机构的分支和子分支。

（1）齿轮五杆机构可看作一个五杆链和一个齿轮链耦合而成，满足式（1）表示齿轮链能连续运动而满足式（9）表示五杆链能连续运动，同时满足式（1）和式（9），齿轮五杆机构才能装配和运动。

（2）式（1）表示齿轮链的输入输出曲线，而式（9）表示五杆链的关节旋转空间。齿轮五杆机构的分支为齿轮链的输入输出曲线与五杆链的关节旋转空公共的部分，每一部分代表了一个分支。

（3）分支点为齿轮链的输入输出曲线（式（1））与五杆链的关节旋转空间边界曲线的交点。齿轮链的输入输出曲线可由奇异点（死点和分支点）分成若干部分，仅满足式（9）的部分为有效分支，也是齿轮五杆机构的分支。

（4）通过式（10）、式（11）识别齿轮五杆机构的子分支。由3.1节可知，每个输入值θ2都可能对应着一个或两个θ3，即在每个分支中，每一个输入可能对应着一种或两种构型，也就是子分支，子分支通过式（10）和式（11）来区分。当Δ1=0，每一个输入对应一个θ3值，机构只存在一种构型，即只有一个子分支；当Δ1>0，每一个输入对应两个θ3值，机构有两个子分支。

3.4 齿轮五杆机构完全旋转性识别

机构的完全旋转性表示机构在整个运动循环中平滑变换而不会遇到死点的能力。要识别机构的完全旋转性，首先应识别机构的分支［10］。如果分支具有完全可旋转性，则输入旋转不会受到限制，在这样的分支中，每个输入值对应于唯一的机构构型。

具有完全可旋转性的机构，其分支中不能存在死点或分支点。也就是说，对于齿轮五杆机构，齿轮链所在直线应满足式（9）或式（12），同时式（1）与式（13）、式（14）之间没有公共解。可通过以下方法来识别齿轮五杆机构分支的完全旋转性：

（1）识别分支点。若齿轮链的特征曲线与五杆链的边界曲线之间有交点，即Δ2≥0或Δ3≥0，分支有分支点；若齿轮链的特征曲线与五杆链的边界曲线无交点，即Δ2<0且Δ3<0，分支无分支点。若存在分支点，则机构不具有完全旋转性。（2）识别机构完全旋转性。若齿轮链所在直线完全在五杆链关节旋转空间内，不存在分支点，则齿轮五杆机构的分支具有完全旋转性。

3.5 实例1

当a1=4，a2=7，a3=4，a4=6，a5=8，n=-1，α=0°时，以θ2为输入，θ5为输出的分支图，如图6所示。

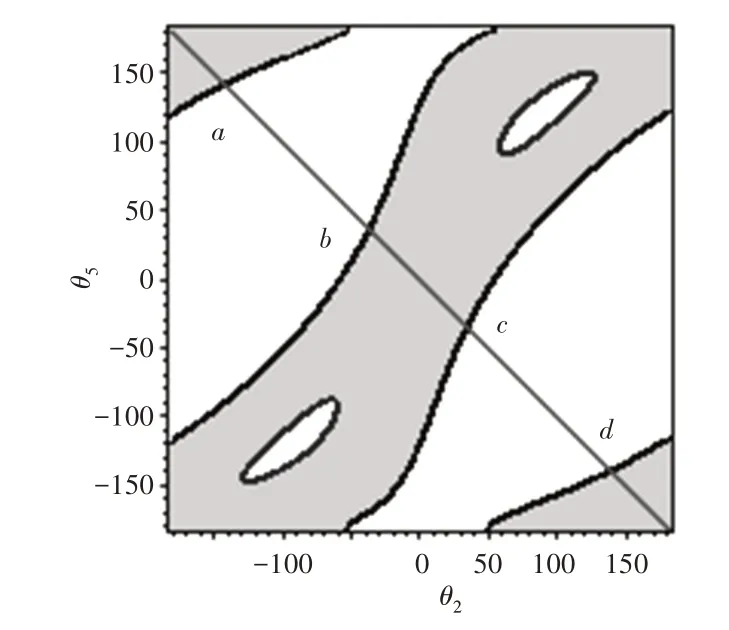
图6 例1的分支图Fig.6 Branch Diagram of Example 1

灰色阴影为五杆链ABCDEA输入与输出的关节旋转空间，代表了五杆链中两输入关节的可行域，黑色曲线表示二杆组BCD处于拉伸共线的奇异构型，蓝色环状曲线表示二杆组BCD处于重叠共线的奇异构型。斜率为-1的直线为齿轮链的特征曲线，代表了齿轮链中输入输出关节的可行域。

齿轮链的特征曲线被五杆机构的关节旋转空间分为若干段，只有公共的部分才是机构的有效分支，位于关节旋转空间外部的部分输入输出曲线表示由五杆链阻碍了齿轮链的可动性。

将机构尺寸代入式（15）、式（16）可得到分支点：a（-148°，148°）、b（-32°，32°）、c（32°，-32°）、d（148°，-148°）。由图6可知，（148～180）°与（-180～-148）°是一个连续的分支，因此，输入关节θ2的运动范围为（-32～32）°、（148～212）°。

分支点处于五杆链边界曲线上，一个输入值只能对应一个θ3值，机构只存在一种构型，处于阴影内的每个点，一个输入对应着两个θ3值，由式（10）、式（11）来区分，分别对应机构的两个子分支。

由于存在分支点，则机构的分支不具有完全旋转性。

4 齿轮链与完全旋转性研究

4.1 完全旋转性的约束条件

在机构设计、综合以及并联机器人应用中，必须保证机构在各精确点之间运动的连续性和平滑性，才能有效避免机构设计和综合中运动缺陷问题［7］。

由第2章可知，齿轮链的传动比及初相角会影响分支点的存在，分支点的存在会影响分支的完全旋转性，而机构的分支是否具有完全旋转性决定了机构是否存在运动缺陷。

要使齿轮五杆机构描绘出完整封闭的连杆曲线，机构必须连续平稳的转动，即齿轮五杆机构的分支要具有完全旋转性，需满足：

（2）齿轮链与五杆链边界曲线没有交点：

（3）齿轮链所在直线完全在五杆链关节旋转空间内。

在机构设计及轨迹综合过程中，将Δ1≥0、Δ2<0及Δ3<0作为约束条件，可避免分支点的存在，避免运动缺陷。

4.2 分支的纠正

不具有完全旋转性的分支是含有运动缺陷的，会阻碍机构的连续运动，因此，应当纠正分支，避免运动缺陷。

齿轮五杆机构是组合机构，当五杆机构参数确定时，Δ1是可以确定的，其奇异曲线及关节旋转空间也是确定的，因此，可通过改变齿轮链的传动比及初相角来纠正分支。

由前文可知，Δ2与Δ3是与五杆机构的尺寸、传动比及初相角相关的方程，当五杆机构尺寸一定时，满足齿轮链输入输出曲线与五杆机构奇异曲线不相交的传动比和初相角有很多组解。

分支要具有完全旋转性，齿轮链所在特征曲线必须完全在五杆链的关节旋转空间内，因此关节旋转空间的形状决定了齿轮链的传动比的取值范围，而传动比的取值决定了初相角的范围。

因此，五杆机构的尺寸确定了关节旋转空间，根据五杆机构的关节旋转空间的形状选择适当的传动比，求解4A2C2<0 和Δ3=即可得到初相角的取值范围。取区间内的初相角与传动比组成的特征曲线，与关节旋转空间没有交点，且完全在关节旋转空间内，满足完全旋转性的要求。

4.3 实例2

五杆机构尺寸为a1=3，a2=9，a3=4，a4=6，a5=9。

将尺寸代入Δ1，得到五杆机构的关节旋转空间。关节旋转空间为斜率为1的条形区域，要使齿轮五杆机构的分支具有完全旋转性，可以取传动比为1，将传动比及五杆机构尺寸代入Δ2<0和Δ3<0 中，可得到初相角的取值范围为（-6°，6°），（33°，45°），（-45°，-33°），如图7所示。也就是说，当传动比为1时，初相角在取值范围内，齿轮五杆机构的分支是具有完全旋转性的。由图7可知，六条红色直线分别是初相角取区间边界值时的输入输出曲线，分别与五杆链的奇异曲线存在一个交点，机构存在一个分支点。当初相角取区间内的值时，齿轮链所在直线就完全在五杆机构的关节旋转空间内，机构的分支为齿轮链所在直线，没有分支点，具有完全旋转性。

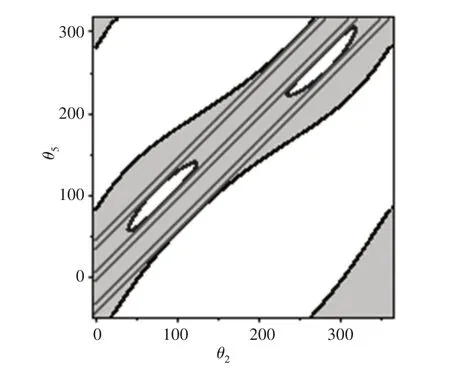
图7 例2的分支图Fig.7 Branch Diagram of Example 2

5 结论

（1）利用Matlab/fsolve函数，结合实例，分析了传动比及初相角对齿轮五杆机构轨迹曲线的影响，结果表明，齿轮五杆机构轨迹曲线的变化具有周期性，变化周期与传动比和初相角有关。（2）对五杆链和齿轮链建立了数学模型，结合实例，利用判别法分析了齿轮五杆机构分支点、分支、子分支及完全旋转性识别过程。（3）分析了齿轮链的两个参数对机构完全旋转性的影响，传动比及初相角的取值会影响分支点的存在，分支点会影响机构分支的完全旋转性，导致机构存在运动缺陷。提出了在机构设计及轨迹综合过程中，将无分支点作为约束条件，来避免运动缺陷的理论方法。（4）针对不具有完全旋转性的齿轮五杆机构，提出了通过改变传动比及初相角来纠正分支的方法，来避免运动缺陷的理论方法，并通过实例进行了验证。（5）齿轮链中传动比及初相角对机构运动规律的影响，为齿轮五杆机构的轨迹优化综合提供了重要的理论依据。