复合台阶绕流中旋涡与强化传热的关联性机理

瞿 磊，谢纬安，喜冠南，张 杰

（1.南通职业大学汽车与交通工程学院，江苏 南通 226007；2.南通大学机械工程学院，江苏 南通 226019）

1 引言

台阶绕流是分离再附流动现象中的典型代表，这种流动现象不仅在自然界广泛存在，在工业中也经常被应用。针对台阶绕流的研究通常在后向台阶、前向台阶、复合台阶以及障碍物流道中进行。后向台阶绕流的研究涉及很多方面，主要包括了后向台阶绕流中侧壁效应引起的三维特性［1-2］，几何参数对流动传热特性的影响［3，4］以及旋涡运动引起的流动不稳定性［5-6］。另一个典型模型前向台阶绕流的研究主要涉及了台阶上下游的回流区流动［7-8］，纳米流体的传热特性［9］以及粗糙表面的流动机理［10］。

复合台阶绕流的研究主要考虑了后向前向台阶，双前向台阶和台阶加障碍物等复合台阶模型。对于后向前向复合台阶，文献［11］通过数值模拟研究了复合台阶流道中的流动自激振荡及其引起的强化传热。文献［12］研究了复合台阶绕流中台阶几何参数对流体振动以及壁面传热的影响，发现流体周期性振动下的传热有明显提升。文献［13］研究了复合台阶流道中弧形引流板对流动传热的影响，结果表明弧形引流板能有效强化台阶之间区域的传热。

对于双前向台阶，文献［14］研究了双前台阶流道中湍流强制对流的传热，结果表明第二个台阶的几何参数对传热有明显作用。在此基础上，文献［15］研究了矩形障碍物在双前向台阶流道中的传热，结果表明增大矩形块的高宽比能够增强湍流下的壁面传热。文献［16］分析了双前台阶流道中障碍物位置对流动传热的影响。

对于台阶流道中带有障碍物的模型，文献［17］数值模拟了矩形障碍物流道中脉动来流的传热特性，分析了斯特劳哈尔数、振动频率以及障碍物间距对传热的影响。在此基础上，文献［18］研究了矩形障碍物间添加旋转圆柱的模型，发现雷诺数、圆柱旋转速度和脉动来流频率均对传热形成影响。文献［19］研究了台阶顶面带矩形障碍物流道中的流动传热，分析了障碍物尺寸的作用。文献［20］的类似研究表明，顶面矩形障碍物位置和高度对传热作用明显，而矩形障碍物的宽度和数量对传热的影响不大。文献［21］进一步研究了台阶流道顶面布置振动翅片的强化传热效果，结果表明振动速度对传热有明显作用，而振动幅度的影响不大。

根据以上文献分析，关于分离再附流动的研究通常以包含单个台阶的流道为主。对于复合台阶绕流，考虑了后向前向台阶，双前向台阶和台阶加障碍物等模型，研究内容主要涉及了几何结构参数以及边界条件对流动传热的作用。但复合台阶绕流中的强化传热机理尚未完全理清，因此，这里针对典型的复合台阶模型展开流动传热研究，首先分析了后向前向台阶流道中的基本流动传热特征，进而考察了主回流区下游周期性旋涡的演变规律，最后，阐明了复合台阶绕流中典型旋涡与强化传热的关联性机理。

2 研究方法

2.1 物理模型及边界条件

研究中涉及的物理模型，如图1所示。采用二维模型主要是因为不考虑侧壁效应时，雷诺数范围400≥Re≥1000下的流动主要表现为二维特征。根据文献［1-2］的研究结果，流动特征是否向三维转变主要取决于侧壁边界条件和台阶模型的高宽比。文中的雷诺数定义为Re=ρuinS/m，式中：台阶高度S固定为15mm，台阶上游壁面的长度为2S，台阶底面长度为12S，流道总长度为60S。流道在后向台阶处的扩张比为2，在前向台阶处的收缩比为0.5。

图1 复合台阶绕流的物理模型Fig.1 Geometry Domain of Combined Step Model

上述物理模型中的边界条件可以表达为：

进口边界处的流动考虑为充分发展流动流，流向速度满足抛物线分布，法相速度为零，进口温度均匀为Tin=283K。

出口边界处的速度、温度边界被认为满足边界层近似定律。

高中关于洛伦兹力的问题多数是关于带电粒子在磁场中的应用，而最让人头痛的便是洛伦兹力在叠加磁场中运动综合运用问题。下面就以2015年高考福建卷11题为例进行分析，(如图5)

流道所有壁面为无滑移边界条件，台阶底面为温度恒定Tw=313K的加热面，其余壁面为绝热壁面。

2.2 控制方程及求解

数值模拟部分做出了以下假设：流体为不可压缩牛顿流体，流动为二维流动，流体物性值为常量。控制方程如下：

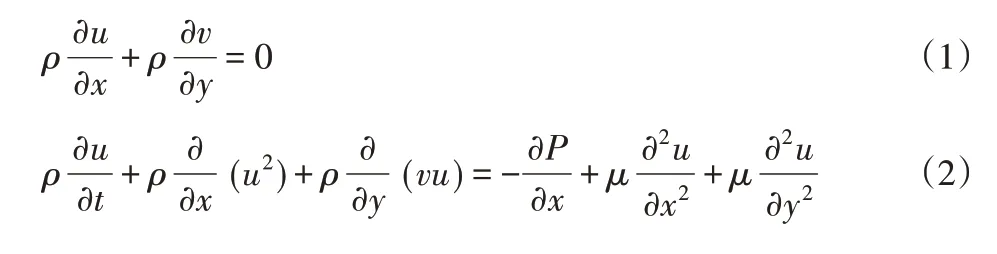
式中：u、v、P和T—流向和法向速度、压力和温度；Cp、r、m和l—定压比热容、密度、动力粘度和导热系数。参数取值为：ρ=1.247kg·m-3、μ= 1.76×10-5kg·m-1·s-1、λ= 0.0251W·m-1·K-1和Cp=1.005kJ·kg-1·K-1。

研究中通过FORTRAN程序编程来求解控制方程，QUICK格式用来离散差分方程中的对流项，ADI算法用来求解全隐式的差分方程。在每个时间步长中，SIMPLE算法用来处理速度-压力耦合问题。流道中计算区域的速度、温度初始条件设定为u=0、v=0和T=283K。

2.3 网格划分及实验验证

在作者之前的研究中，已对后向台阶绕流进行了网格独立性验证。本研究中采用非均匀网格对计算区域进行划分，又通过考察Re=700时复合台阶绕流底面时均努塞尔数对网格独立性进行了验证。网格独立性验证结果，从图中可以看出，沿着整个底面时均努塞尔数的局部最大偏差不超过8%，如图2所示。因此，网格数为（642×101）的网格能够准确计算研究中涉及的流动传热问题。

图2 网格独立性验证结果Fig.2 Test Results of Grid Independent Study

为了验证数值模拟结果的准确性，通过闭式循环水槽试验台和PIV系统对后向台阶绕流进行了流动实验，如图3、图4所示。循环水槽包括了水箱、水泵、整流段、收缩段、发展段、实验段和流量计等主要组成部分。PIV系统主要包括了激光器、CCD相机和同步控制器。实验段的尺寸为台阶高度S=15mm，台阶扩张比和宽高比分别为2和16。

图3 闭式循环水槽实验台的实物图Fig.3 Physical Map of the Closed Loop Water Tunnel

图4 PIV系统的布置Fig.4 Arrangements of PIV System

根据以上实验系统，测得了主回流区时均在附着点的位置。通过实验结果和已有文献的结果对数值模拟结果进行了验证，如图5 所示。从图中可以看出，数值模拟结果与实验结果以及文献［22］的研究结果吻合较好，与文献［23］的研究结果在Re≥400后出现偏差主要是因为实验方法以及模型的几何尺寸不同引起。以上验证表明这里的数值模拟方法准确可靠。

图5 不同雷诺数时的时均在附着点位置Fig.5 Time-Average Reattachment Point Positions for Different Reynolds

3 结果与讨论

3.1 基本流动传热特性

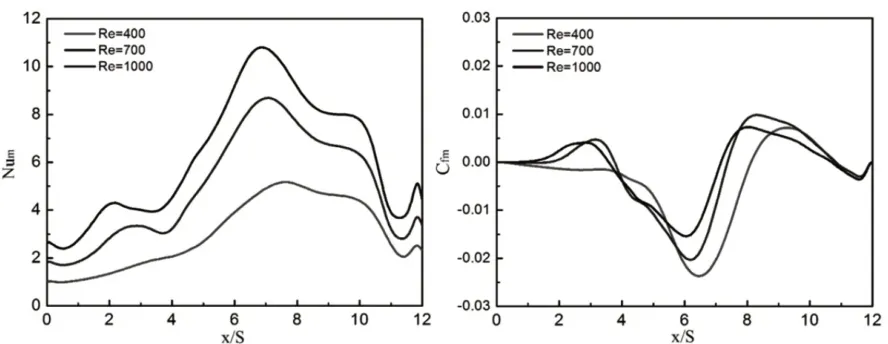
图6 不同Re时底面的时均努塞尔数和时均摩擦系数Fig.6 Time-Average Nusselt Number and Skin Friction Coefficient for Different Reynolds Numbers

从图6中可以看出，各工况下Num呈现先增大后减小的趋势，在附着点附近形成一个较大的峰值，主回流区内以及前向台阶上游均形成一个较小的峰值。图中雷诺数从（400～700）时Num的增长要明显大于雷诺数从（700～1000）时的增长，这体现出了Num随雷诺数的非线性增长特征。各工况下的Cfm曲线表现为先减小后增大的趋势，下降趋势中谷值的绝对值随雷诺数的增大而减小，上升趋势中峰值的大小随雷诺数的变化不大。总体上，在再附着区域出现了时均非相似性（Num增大的同时Cfm减小）。随着雷诺数的增大，产生时均非相似的区域逐渐减小，Re=400时非相似的区域为x/S=6.5 到x/S=7.6，而Re=700和Re=1000时非相似的区域分别减小为x/S=6.2 到x/S=7.1和x/S=6.1到x/S=6.9。形成这种非相似性的原因值得进一步深入研究。

不同雷诺数下流道中的时均速度流线和温度场，如图7、图8所示。时均速度流线图中，不同工况时均在后向台阶下游，顶面附近以及前向台阶上游分别形成回流区。图6中的较大的Num峰值由主回流区的流体再附着引起，而前向台阶上游的回流运动引起了Num曲线在前向台阶上游的较小峰值。随着雷诺数的增大，主回流区的尺度逐渐减小并主回流区内形成一个逆时针旋转的近壁回流涡，这一旋涡的形成促使Re≥700后Num曲线在主回流区内形成较小的峰值。时均温度场中，各工况下的温度场形态相似。早期过渡流区域，高温流体聚集在后向台阶下游和前向台阶上游的回流区中，温度边界层随雷诺数的增大而变薄。

图7 不同Re时的时均速度流线与速度场Fig.7 Time-Average Streamlines and Velocity Vectors for Different Reynolds Numbers

图8 不同Re时的时均温度场Fig.8 Time-Average Temperature Fields for Different Reynolds Numbers

为了深入阐明图6中流动传热特性的形成原因，考察了不同雷诺数下的瞬时速度流线和瞬时温度场，如图9、图10所示。瞬时速度流线在不同区域均出现了流动不稳定性，主回流区中形成类泰勒旋涡，再附着区域下游出现交替旋涡。主回流区中的流动不稳定性随雷诺数的增大逐渐增强，促进了图7中近壁小尺度旋涡的形成，同时旋涡的形态也随流动不稳定性的改变而改变。瞬时温度场中，主回流区下游产生了较明显的温度波动，该温度波动由流道中的近壁旋涡引起，能够加强高温流体和低温流体的混合从而强化局部传热。在Re=1000时，温度波动的范围延伸到了主回流区的剪切层。总体上，温度波动的范围和强度都随雷诺数的增大而增大。

图9 不同Re时的瞬时速度流线与速度场Fig.9 Instantaneous Streamlines and Velocity Vectors for Different Reynolds Numbers

图10 不同Re时的瞬时温度场Fig.10 Instantaneous Temperature Fields for Different Reynolds Numbers

3.2 强化传热机理

上述分析理清了不同雷诺数下复合台阶绕流的基本流动传热特征，在此基础上选取Re=700 时的工况来考察不同监测点A（x/S=8，y/S=1），B（x/S=10，y/S=1）和C（x/S=10，y/S=1.5）的速度振动特征。这些测试点法向速度随时间的振动特征以及所对应的能量谱密度，如图11所示。

图11 Re=700时监测点的速度及其能量谱密度Fig.11 Velocity and Power Spectral Density for Test Points at Re=700

Re=700时一个振动周期不同时刻的流线及流向速度场图，如图12所示。由图12可知，一个振动周期内的流动演变出现了三种典型的旋涡，分别是由从回流区中分离出的旋涡A，再附着点下游的旋涡B以及主回流区中新生的旋涡C。这些旋涡随着时间存在演变关系，又同时在流道中存在，一个周期的初始时刻，旋涡A0和旋涡B0随时间发展演变。在t=t0+5Δt时，由于几何结构中前向台阶的阻挡效应，旋涡B在该时刻消失，同时旋涡A5代替了之前时刻B类旋涡的角色，主回流区内新生旋涡C5也在不断地发展将代替之前的A类旋涡。新生的C类旋涡主要是由于主回流区剪切层中的Kelvin-Helmholtz 不稳定性和回流区内的Tay⁃lor-Grtler不稳定性相互作用诱导生成。以上分析基本上阐明了一个振动周期内旋涡的形成原因及演变特征。

图12 Re=700时一个周期内不同时刻的流线和速度场Fig.12 Streamlines and Velocity Fields in the Periodic Cycle at Re=700

与图10中时刻相对应的瞬时努塞尔数（Nu）和瞬时摩擦系数（C）f曲线图，如图13所示。从图13中可以看出，周期性的旋涡演变促使Nu和Cf曲线沿着底面形成了明显的波动。Nu曲线形成了两个主要的峰值，第一个峰值主要由A类旋涡引起，第二个峰值主要由B类旋涡引起，峰值的大小也与旋涡的演变特征密切相关。此外，由于Taylor-Grtler 不稳定性的影响，Nu曲线在主回流区内还出现了一个较小的峰值。在不同时刻，Cf曲线中同样出现了相应的峰值和谷值，Cf峰值主要由于局部流体的加速效应引起，而谷值则是由旋涡的回流运动引起。峰值和谷值大小的直接影响因素是局部流体剪切应力的大小。同时在图中可以发现，局部区域的瞬态流动和传热存在非相似性（传热提升的同时流阻下降），对这种现象的合理利用能有效提高换热设备的性能。根据对图12和图13中一个振动周期内流动传热特征的分析，初步建立了一个早期过渡流下的旋涡分析模型来考察旋涡运动和传热强化之间的关联性机理。Lv和Hv分别表示旋涡长度和旋涡高度，γ和Ω分别表示旋涡再附着冲击角和近壁冲击流速，如图14所示。基于这个分析模型，图12中旋涡A2比旋涡A0的冲击角大，促使图13中Nu峰值PA2大于峰值PA0。同时Nu峰值PB1小于峰值PB0主要是因为旋涡B2后方的流动受到前向台阶的抑制作用，旋涡冲击流速下降而造成。图12中旋涡A7的回流长度比旋涡C7小，这就造成了图13中Nu峰值PA7和PC7有不同的曲线特征。从以上分析可以看出，旋涡再附着冲击角γ，近壁冲击流速Ω和旋涡流向长度Lv是影响旋涡附着区域传热的三个关键因素，较大的冲击角和近壁流速能够有效的破坏壁面边界层并加强流体的混合，不同的旋涡长度则会影响旋涡区域Nu曲线的变化率。总体上，旋涡区域的局部传热将随着γ和Ω的增大而增大。

图13 Re=700时一个周期内不同时刻的努塞尔数和摩擦系数Fig.13 Nusselt Number and Skin Friction Coefficient Distributions in the Periodic Cycle at Re=700

图14 过渡流下的旋涡分析模型Fig.14 Preliminary Evaluation Model of the Vortex in the Transitional Flow

4 结论

这里以复合台阶绕流为对象研究了早期过渡流下典型旋涡与强化传热的关联性机理。

重点分析了周期性的旋涡演变及其对壁面传热的作用，主要得出了以下结论：

（1）从层流到早期过渡流Num表现出了非线性的增长特征，传热随雷诺数增长速率最大的位置发生在层流向过渡流转变的区域。早期过渡流下的Num和Cfm表现出了局部非相似性，该非相似性的区域随雷诺数的增大而减小。

（2）过渡流下的流动和传热不稳定性有所增强，这引起了旋涡形态的变化以及台阶底面上方的温度波动。在流动的周期性演变过程中，流道中出现了三类典型旋涡，分别是由从回流区中分离出的旋涡，再附着点下游的旋涡和主回流区中新生的旋涡。这些旋涡的运动及演变对局部传热有显著的影响。

（3）根据建立的旋涡评价模型，旋涡再附着冲击角γ，近壁冲击流速Ω和旋涡流向长度Lv是影响旋涡附着区域传热的三个关键因素。γ和Ω主要影响Nu峰值的大小，Lv主要影响Nu曲线的变化形态。一般情况下Nu的峰值将随着γ和Ω的增大而增大。