函数的几种数学模型应用探究
■贵州省晴隆民族中学 岑春静
函数是高中数学知识的主线之一,也是高考的难点,要注意对函数基本性质的归纳总结,特别是函数的最值、对称性、零点等问题。求函数的参变量问题是高考的热点,我们在学习的过程中也要加强归纳总结。
题型一、形如函数f(x)=(x>0)的图像问题
结论1:若函数f(x)=(x>0)在区间(0,e)上为单调递增函数,在区间(e,+∞)上为单调递减函数,则当x=e时,函数f(x)=(x>0)取得最大值为。
证明:函数f(x)=的定义域为(0,+∞),f'(x)=。当f'(x)>0,即0<x<e时,函数f(x)为单调递增函数;当f'(x)<0,即e<x时,函数f(x)为单调递减函数。又f'(e)=0,故当x=e时,函数f(x)=(x>0)取得最大值,最大值为。
例1已知a>0,且a≠1,函数f(x)=。
(1)当a=2时,求函数f(x)的单调区间。
(2)当函数y=f(x)与直线y=1 有且仅有两个交点时,求参变量a的取值范围。


题型二、函数的中心对称问题
结论2:如果函数f(x)对任意x∈D,恒有f(a-x)+f(b+x)=c,那么函数f(x)的图像关于中心对称。

例2已知函数f(x)的定义域为R,且满足条件f(-x)=2-f(x),若y=和y=f(x)的交点为(x1,y1),(x2,y2),(x3,y4),…,(xm,ym),则=()。
A.0 B.mC.2mD.4m

题型三、函数的对称性问题
结论3:若函数f(x)满足f(a+x)=f(b+x),则函数f(x)关于直线x=对称。
例3已知函数f(x)的定义域为R,且满足f(x)=f(2-x),当函数y=|x2-2x-3|与y=f(x)的交点为(x1,y1),(x2,y2),(x3,y4),…,(xm,ym),则=()。
A.0 B.mC.2mD.4m
解析:因为函数f(x)=f(2-x),所以f(x)的图像关于直线x=1对称。又因为函数y=|x2-2x-3|也关于直线x=1对称,所以两函数的图像的交点也关于直线x=1对称,不妨设x1<x2<x3<…<xm,则x1+xm=x2+xm-1=…=xm+x1=2,故。
题型四、函数的奇偶性问题
结论4:若函数f(x)是奇函数,且g(x)=f(x)+c,则g(-x)+g(x)=2c。
证明:由于函数f(x)是奇函数,所以f(-x)=-f(x),故g(-x)+g(x)=f(-x)+c+f(x)+c=2c成立。

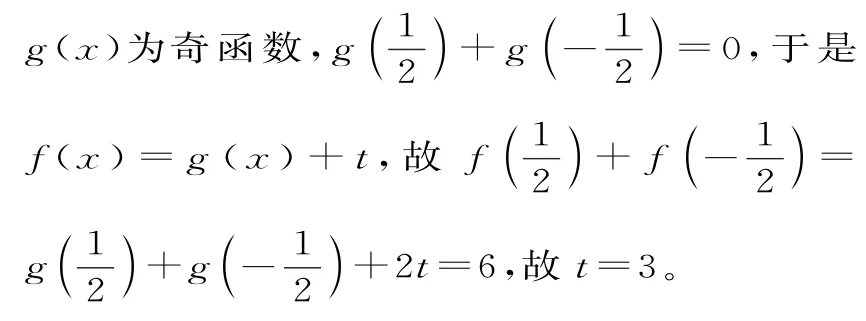
结论5:已知函数f(x)是定义域D上的奇函数,则f(x)对任意的x∈D,都有f(x)+f(-x)=0成立。特别地,当奇函数f(x)在D上有最大值和最小值时,则f(x)max+f(x)min=0。

结论6:若函数f(x)为偶函数,则f(x)=f(|x|)成立。
证明:当x≥0 时,|x|=x,故f(x)=f(|x|);当x<0时,f(|x|)=f(-x),由函数f(x)是偶函数,得f(-x)=f(x)。所以f(|x|)=f(x)成立。
例6已知函数f(x)=ln(1+|x|)-,若使得f(x)>f(2x-1)恒成立,则参变量x的取值范围为____。
解析:函数f(x)的定义域为R,且f(x)是偶函数,当x≥0 时,f(x)=ln(1+x)-,故f(x)是增函数,所以f(x)>f(2x-1)⇒f(|x|)>f(|2x-1|),所以|x|>|2x-1|,故<x<1。
综上所述,函数的最值、单调性、对称性、中心对称、奇偶性是高考考查的热点,对同学们的综合能力、创新能力有很高的要求,因此,在平常的学习过程中要认真总结归纳,不断反思。

