基于GA-小波-BP神经网络的装备维修能力评估*

赵黎兴，侯兴明，徐兆文，和林子

（航天工程大学 航天保障系，北京 102206）

0 引言

随着装备信息化、智能化和复杂程度日益提升，装备维修依靠承研承制单位和维修资质企业等专业维修力量的特征越来越明显，社会化维修已逐渐成为装备维修的主要方式。然而，由于维修力量筛查遴选机制的不健全和维修能力评价方式方法的不客观，导致装备的维修质量参差不齐，严重影响装备性能的发挥和完成任务的质量。因此，开展装备维修能力评估研究具有重大的现实意义。冯宇等［1］在构建了装备维修能力评价指标体系的基础上，将14个指标数据和评价结果作为BP（back propagation）神经网络模型的输入和输出，对某型复杂装备的维修能力进行了评估。但未考虑指标特征信息冗余和初始网络权重/阈值对BP神经网络影响。连云峰等［2］在建立评估指标体系的基础上，利用美国国防部体系架构框架（department of defense architecture framework，DoDAF）模型对装备的维修保障能力进行了评估，但利用统计和专家评估结合的方法对静态指标和动态指标的取值存在主观性强、缺乏基础数据支撑和评估结果误差偏大等问题。朱敦祥等［3］构建了军民融合维修保障能力评估指标体系，利用云理论和物元理论通过熵权法和均方差方法对不同单位的维修保障能力进行了评估。但通过调查和咨询专家构建标准云的方法存在易受调查范围、被咨询专家领域和知识程度的影响，极易导致结果不准确和误差较大。任佳成等［4］利用层次分析法对构建的装备维修能力评价指标体系进行了实际应用研究，但在实际应用中，评估结果对专家经验和知识水平有很强的依赖性，很难形成统一的认识和具有实际意义的评估结果。

以上方法都是通过对指标的优化、组合和指标值的设定，利用数理统计的方法对维修能力进行评估。但是，随着装备的复杂程度越来越高，维修能力评估的非线性、开放性、复杂性和动态性特征越来越明显，使得装备维修能力评估的难度加大，传统评估方法的不适应和低效用越来越明显。BP神经网络结构简单，具有自组织、自学习和自适应性的特点，能够以任意精度和不同方式逼近任意非线性函数。误差的反向传播反复修正网络的权值/阈值，实现实际输出和期望输出差异的最小化［5］。但随机选取的初始阈值和权值容易造成网络的局部收敛、网络的震荡和训练结果差异较大等问题。因此，本文利用遗传算法（genetic algorithm，GA）全局寻优特性和稳健性［6］优化BP神经网络初始权值/阈值，通过小波函数作为隐含层传递函数增强网络的学习功能。将经过属性约简的样本数据作为GABP神经网络模型的输入，评估结果作为模型输出，经样本数据的网络训练和验证，实现对装备维修能力的评估。GA-小波-BP发挥了BP神经网络的泛化映射能力和分类器特性，避免了局部收敛问题，提高了能力评估的分类精度和网络的学习能力。

1 模型构建基础

装备维修记录是对维修基本信息、物资消耗、时间消耗、维修质量等的真实记录，是衡量承修方维修能力的重要数据来源。维修记录数据主要来源于维修企业历次维修统计和维修完成后针对装备使用单位的一线岗位人员和机关业务部门开展的装备维修满意度调查问卷的总结。经调研发现，某维修企业的维修记录属性多达20多项，部分属性间存在相似性和强相关性。为避免因属性冗余造成的网络局部收敛和精度差等问题，本文采用属性主分量约简算法对维修记录属性进行约简。

1.1 粗糙集理论

粗糙集理论的核心内容是通过属性约简消除数据的冗余属性实现降维和特征提取。常见的粗糙集属性约简算法有：基于正区域的属性约简算法、基于差别矩阵的属性约简算法和基于信息熵的属性约简算法［7］。本文通过构造差别矩阵和粗糙集分量函数构建属性最优约简集。

1.1.1 区间值决策系统

区 间 值 决 策 系 统［8］可 以 表 示 为：S=(U，C∪D，V，f)，其中U={χ1，χ2，…，χn}是论域，对象用χ1表示；A=C∪D={a1，a2，…，am}是论域对应的属性集（非空有限集），uk i为属性ak(k=1，2，…，m)下 对 象χi(i=1，2，…，n)的 实 际 值，。C={c1，c2，…，ci}为 条 件 属 性 集，D={d1，d2，…，d j}为决策属性集是属性集A的值域；f表示对象χn在属性am约束下到值域V的度量函数，即f：U×A→V，a∈A，χ∈U，f(χ，a)∈Va。

1.1.2 相似度

相似度表示在同一属性下2个区间值数据之间的相似程度，通过相似度可以得出数据之间的相关关系，具体的方法如下：

定义1假设区间值决策系统S=(U，C∪D，V，f)，属性ak∈C下和的Jaccard相似度ςkij定义为［9］

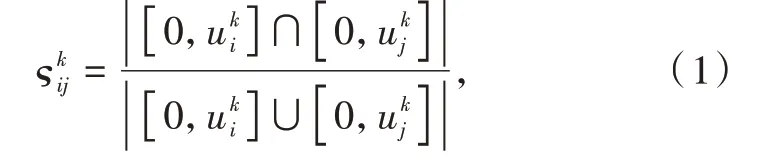
式中：|·|为区间长度。设定相似度阈值δ∈[0，1]，当≥δ时，ak(χi)与ak(χj)两者相容<δ时，两者相离。

1.1.3 属性主分量约简算法

假设有区间值决策系统S=(U，C∪D，V，f)，差别矩阵为M=(cij)n×n的矩阵，cij为差别矩阵中第i行、第j列的元素，cij满足以下条件：

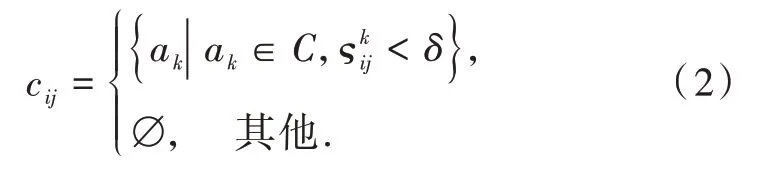
在差别矩阵基础上利用主分量启发式算法构造属性分量函数，属性ak分量函数为［10-11］

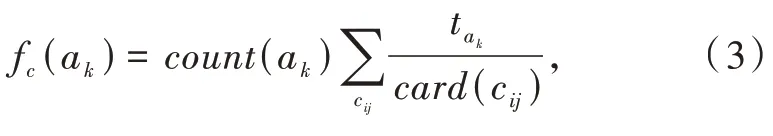
式中：

card(cij)为差别矩阵集合基数；count(ak)为属性ak出现的次数。

属性ak的分量函数的大小反应了属性ak的重要程度，通过属性分量函数可以有效避免属性冗余。属性主分量约简算法具体步骤如下：

（1）求相似度阈值δ∈[0，1]条件下的差别矩阵M=(cij)n×n，将单个核属性加入约简集，即

（2）依据式（3）计算差别矩阵中各属性分量的值，将属性按照分量函数值fc(ak)的大小降序排列。

（3）将所需的前x位fc(ak)加入到属性的约简集，得到最优的属性约简集{}。具体实现过程如图1所示。

图1 粗糙集主分量约简算法示例Fig.1 Rough set principal component reduction algorithm example

主分量约简算法不用对差别矩阵进行简化处理，减少了搜索和遍历决策表的次数，对于有核和无核的决策表均可通过分量函数得到约简集，在相似度阈值δ=0.7，fc(ak)值为前14位属性约简后的维修记录表如表1所示。

表1 XX维修公司经属性约简的维修记录表Table 1 Maintenance r ecords of XX maintenance company after attr ibute r eduction

1.2 BP神经网络

神经网络是一种通过模仿动物神经网络特征，进行大规模分布式信息并行处理的机器学习算法，是一种非线性的动力学系统，在解决多因素和多条件的模糊信息处理问题中有很强的适用性［12］。

1.2.1 信号的单向正向传播

BP神经网络是一种信号单向正向传播，误差反向传播的前项多层反馈的前馈型神经网络算法，利用梯度下降法对网络的权值/阈值进行逐步调整，达到网络模型中每一组输入都能达到理想输出的目的［13-14］。Kolmogorov定理和实践表明：含有一个隐含层的3层BP神经网络能在闭区间内以任意精度逼近任意非线性函数的能力［10］。因此，本文采用3层的神经网络进行维修能力的评估。具有1个隐含层的3层BP神经网络如图2所示，设各层的神经元数目分别为：输入层I，隐含层M，输出层O，ωim和ωmo分别为输入层与隐含层、隐含层与输出层的权值，λ和β分别为输入层与隐含层，隐含层与输出层的阈值。

图2 BP神经网络结构图Fig.2 BP neural network structure diagram

隐含层和输出层的激活函数分别为h(x)和g(x)，u和v分别表示各层神经元的输入和输出，输出 期 望b=(bj1，bj2，…，bjo)，样 本 集 为X=(xj1，xj2，...，xji)，j=1，2，...，n，i为输入层神经元的个数，则隐含层的输入为［15］

隐含层的输出为

输出层的输入为

输出层的输出为

1.2.2 误差的反向反馈

采用梯度下降法按照输出层、隐含层、输入层的顺序对各层的阈值和权值进行调整，使神经网络输出经不断调整更加接近输出期望值。

第j个样本输入时，输出层神经元o的误差为

输出层误差能量的总和为

按照梯度下降法

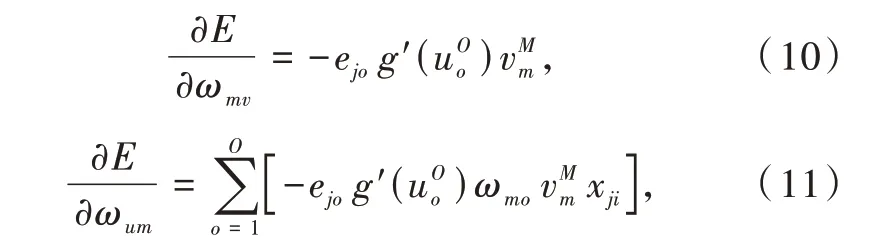
输出层权值调整Δωmo为

输出层阈值调整Δβm为

隐含层权值调整Δωim为

隐含层阈值调整Δλi为

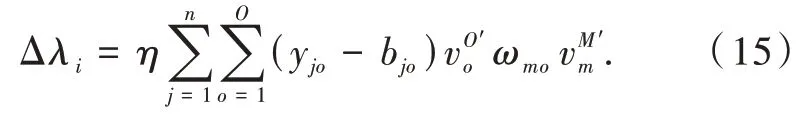
1.3 GA-小波-BP神经网络

由于神经网络初始的权值和阈值为某一区间内的随机值，初始值选取不当会造成网络局部收敛和震荡。利用遗传算法（GA）全局寻优特性优化BP神经网络初始的权值和阈值，避免BP神经网络因局部极值导致局部收敛和收敛速度过慢的影响，为增加网络的学习功能，提高网络训练速率和训练精度，选取小波函数作为隐含层的传递函数［16-17］，Sig‑moid函数为输出层激活函数。GA-小波-BP神经网络模型进行维修能力评估的流程如图3所示。

图3 GA-小波-BP神经网络流程图Fig.3 GA-wavelet-BP neural network flow chart

遗传算法从最开始选定的初始阈值和权值种群，利用选择复制、随机交叉和变异，通过种群优胜劣汰实现种群渐进式的逐代优化，进而不断逼近最优解［18］。GA优化BP神经网络具体步骤如下：

（1）种群初始化

在一定的区间内随机选择BP神经网络的初始阈值和权值，按照输入层-隐含层-输出层权值和阈值的顺序组成遗传算法的种群个体。遗传算法种群个体一般采用二进制编码，由于BP神经网络初始的权值和阈值为一随机数，采用二进制编码容易导致位串过长，影响网络的寻优速率，因此采用实数对种群个体进行编码。

（2）设定适应度函数

适应度函数通常由求解问题的目标函数转化而来，本文中目标函数为误差能量的求解问题，要求误差能量越小越好，而适应度函数优化BP神经网络的权值和阈值要求个体优化程度和被选择的概率越大越好，因而，选择适应度函数为［19］

种群中个体j的适应度值为F j，fj为Fj的倒数，fj越大，适应性越好。

（3）选择遗传算子

遗传算法的选择操作是优胜劣汰的过程，即挑选出优良个体和淘汰不满足要求的个体，挑选出的个体作为父代繁殖子代。常用的遗传算法的选择方法有随机遍历选择法、基于种群交流的选择法、适应度比例选择法和局部选择法等［15］。本文采用基于适应度比例选择的Monte Carlo法［20］。设初始阈值和权值的种群数量为N，种群中个体的选择概率Pj为

（4）交叉遗传算子

从经选择操作保留的优良个体的父代中，随机选择2个个体θi和θj，随机独立地选择交叉位l进行染色体的交叉操作，具体如下：

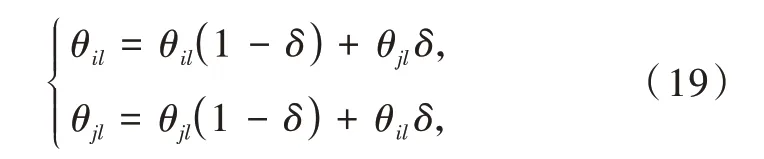
式中：δ为[0，1]的随机数。

（5）变异遗传算子

遗传算法变异操作是，随机选取的种群个体以很小的概率随机改变个体编码数据中某个串的值完成均匀变异，达到提高个体适应度和局部逼近最优解的目的。本文采用均匀变异的方法，变异后的新个体为

式中：θmin和θmax为初始种群个体的最小、最大值；ε为[0，1]的随机数。

（6）个体评价

评价个体适应度是否满足要求，若不满足，则进行再次循环迭代，直到满足网络要求。

（7）解码

将符合要求的个体按照编码的逆过程进行解码，本文使用实数编码，不存在解码过程。

（8）赋值

将获得的最优阈值和权值作为BP神经网络的初始阈值和权值进行网络训练。

2 基于GA-小波-BP的装备维修能力评估

2.1 数据预处理

装备维修数据记录中数据量纲不同，标准不统一，需要对数据进行标准化处理。

2.1.1 等级数据的处理

（1）维修等级、技术等级数据的处理

调研得知，该企业装备维修等级分为4类：①维修为装备的核心部件损坏或核心功能无法实现，故障点位多，故障定位难，维修时限要求高，维修困难；②维修为装备的重要功能存在故障，部分功能无法实现，故障定位较难，故障数量较多，维修难度较大；③维修为装备的状态不稳定，技术性能达不到指标要求，故障排查任务量大，一般需要换件和较简单的原位修理，维修难度较低；④维修为装备发生一般故障，故障数量较少，故障定位容易，维修难度低。维修人员的技术等级由高到低分为1，2，3，4，5，6个等级，本文参照比例法，对维修等级、技术等级按照公式（21）进行定量化：

式中：i为单次维修中维修装备数量或维修人员数量；zij为第j次维修中第i个装备的维修等级或第j次维修中第i个维修人员的技术等级。

（2）其余等级数据的处理

该企业将维修设备、维修材料按照等级的由高到低依次划分为1，2，3和1，2，3，4等级，为保证原始数据的真实性和一致性，采用比重法对等级数据进行处理，公式如下：

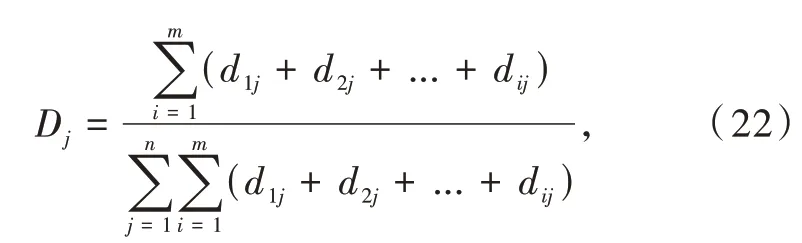
式中：i为单次维修中维修设备、维修材料的数量；d ij为第j次维修中第i个维修设备和维修材料等级。

2.1.2 其他维修记录条件属性数据的处理方法

为保持原始数据的真实性，本文采用比例法对其余各项属性数据进行归一化进行处理，公式如下：

式中：ci为维修记录中的第i个属性；j为维修的次数；xij为第j次维修，第i个属性的值。ci∈[0，1]且无量纲。

2.2 基于遗传算法（GA）优化BP神经网络的构建

结合该企业的维修记录表，网络的输入层为维修记录中的属性a1～a14，输出层为含有一个神经元的维修能力评价结果，依据维修记录中维修能力评价的标准，依次划分为优（0.82～1］，良（0.62～0.82］，中（0.45～0.62］，差（0～0.45］，隐含层神经元的个数按照公式（24）得到。

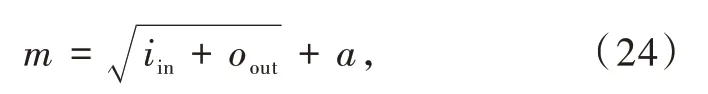
式中：m，iin，oout分别为隐含层、输入层、输出层神经元的个数；a为[1，10]之间的整数。

本文中BP神经网络隐含层的传递函数使用小波函数，输出层的激活函数使用Sigmoid函数g(x)=，小波函数作为隐含层传递函数时，隐含层和输出层的输出如式（25），（26）所示：

式中：H(·)为函数hi(·)经傅里叶变换后的函数［21］；ai为度量hi的收缩因子；bi为度量hi的平移因子。

隐含层不同神经元数目的训练误差如表2所示。经网络训练，最终确定隐含层神经元的个数为10个。

表2 隐含层不同神经元数目的训练误差Table 2 Training errors of different numbers of neurons in the hidden layer

在14个记录属性作为输入，10个隐含层神经元和输出层1个神经元的GA-BP神经网络结构中，需要优化的网络权值个数为14×10+10=150，网络阈值个数为10+1=11，总有165个变量。遗传算法优化参数的设置如表3所示。

表3 遗传算法优化参数设置Table 3 Genetic algorithm optimization parameter settings

3 模型应用与结果分析

BP神经网络输出精度和训练速度主要受初始阈值、权值、网络结构和网络训练函数的影响。本文选取某维修资质企业近4年的维修记录283组数据为样本，选取其中的270组数据作为模型的训练样本，按照上述数据的处理方法对数据进行归一化，其中部分数据如表4所示。

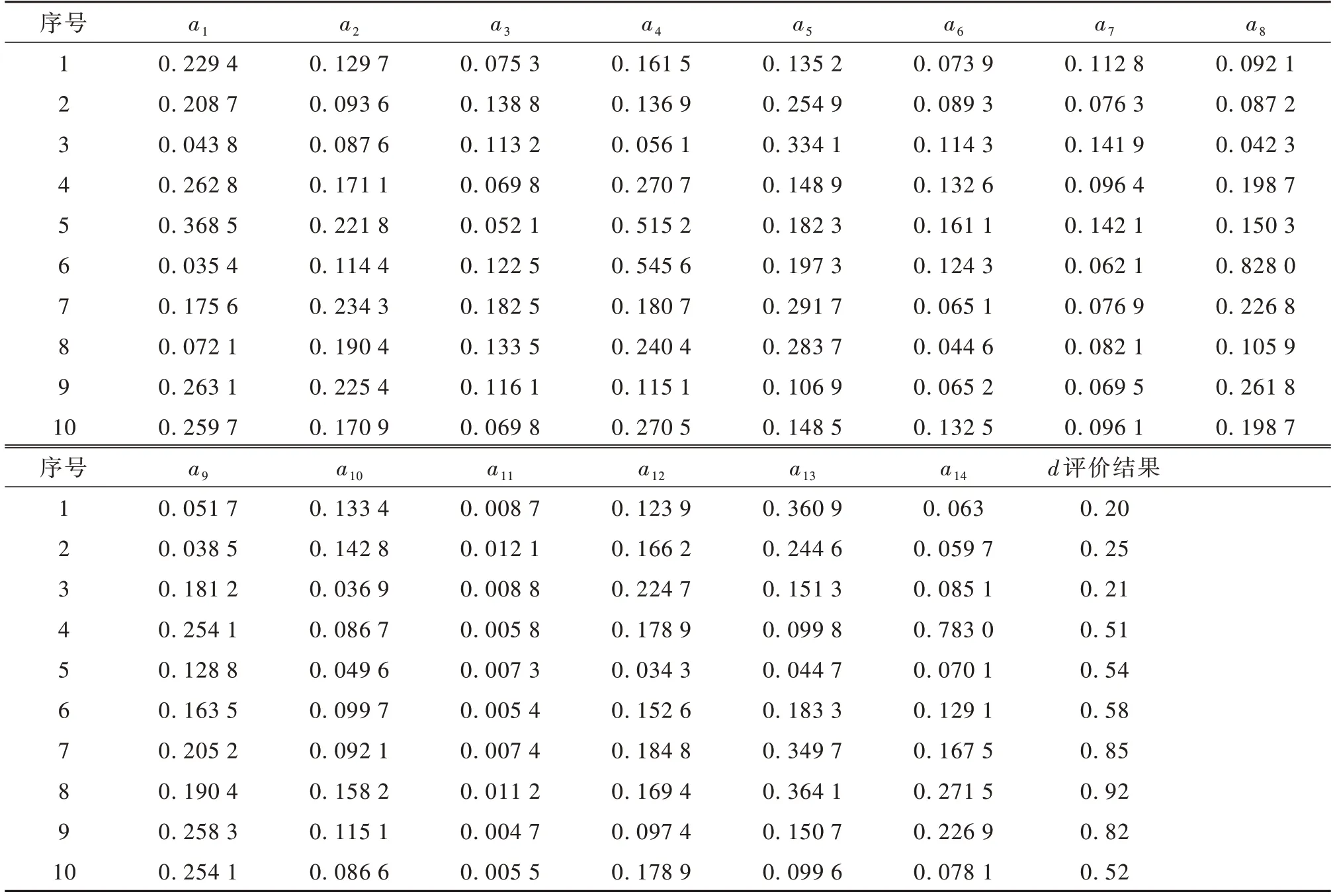
表4 数据处理后的某维修企业维修记录表（节选）Table 4 Repair r ecord form of a maintenance company after data pr ocessing（excer pt）

将第1～270组数据作为训练样本输入模型，设置训练精度为10-5，学习速率为0.1，最大迭代次数为1 000，利用Matlab软件进行训练。当训练样本中的一部分数据存在很大偏离时，可以用异常值检测算法对异常数据进行检测，然后用平均值、中位数或者其他处理方法对异常值进行替换或删除。当一些数据偏离很小时，可以看作是数据噪声，一般对模型的训练效果影响很小，不作处理。BP神经网络训练输出误差变化曲线如图4所示，在迭代至第12步时，网络达到收敛和最佳验证性能误差0.057 019。

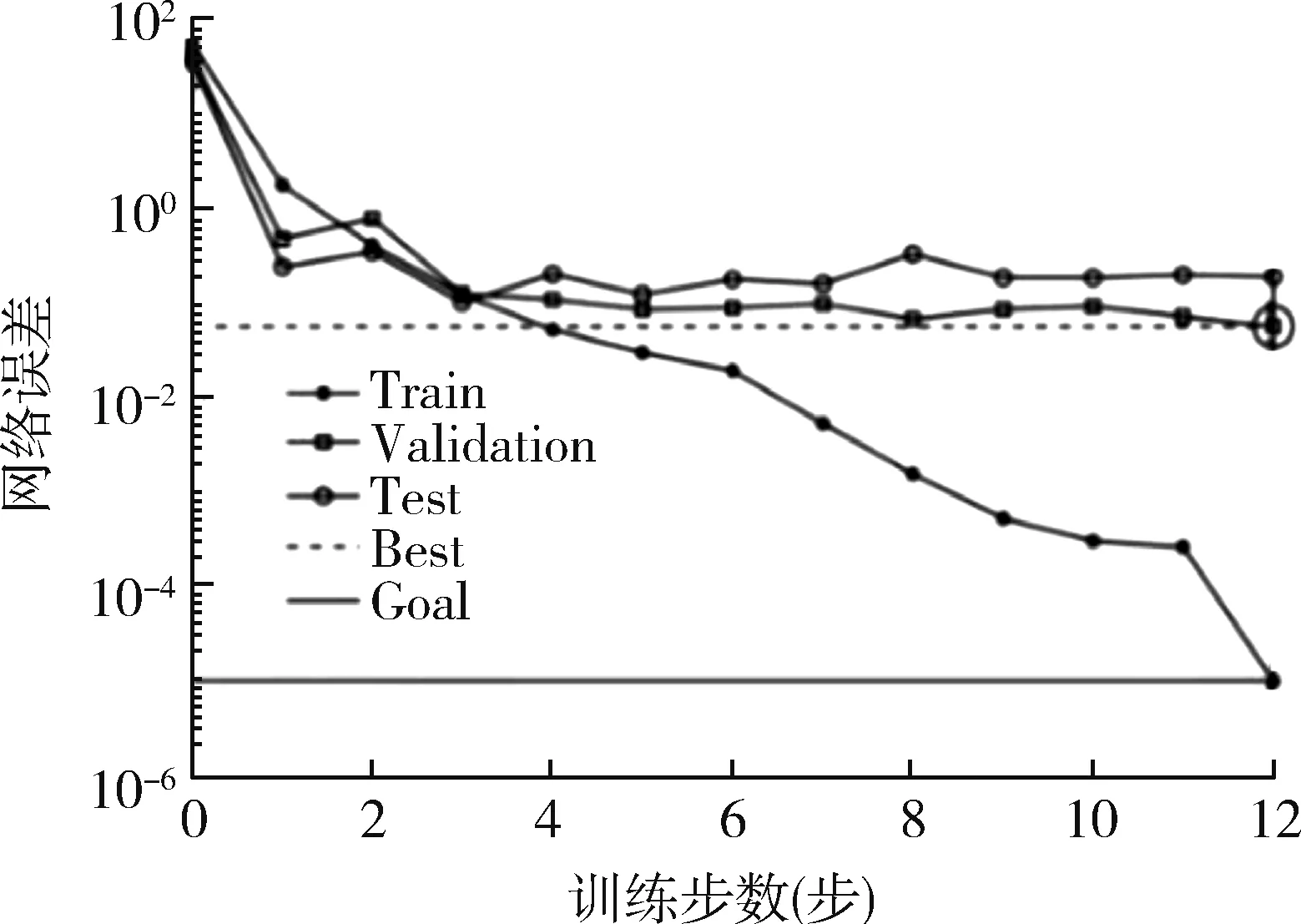
图4 BP神经网络误差曲线Fig.4 Error curve of BP neural network

利用GA-BP网络结构，采用同样的训练样本，学习率为0.01，不设置目标值，迭代完为止。在迭代至第3步时，网络达到最佳验证性能误差0.055 629；在迭代到第9步时，完成迭代，网络收敛，如图5所示。

图5 GA-BP神经网络误差曲线Fig.5 GA-BP neural networ k er ror cur ve

GA-BP，GA-小波-BP的适应度变化曲线如图6，7所示，GA-小波-BP的平均适应度远远小于GA-BP的适应度，即GA-小波-BP的误差能量远远小于GABP的误差能量，具有更小的误差输出。GA-小波-BP平均适应度曲线在22代趋向平缓，网络可获得最优个体；而GA-BP平均适应度曲线在38代趋向平缓，获得最优个体。用小波函数代替BP神经网络的传递函数，网络的收敛速度更快。

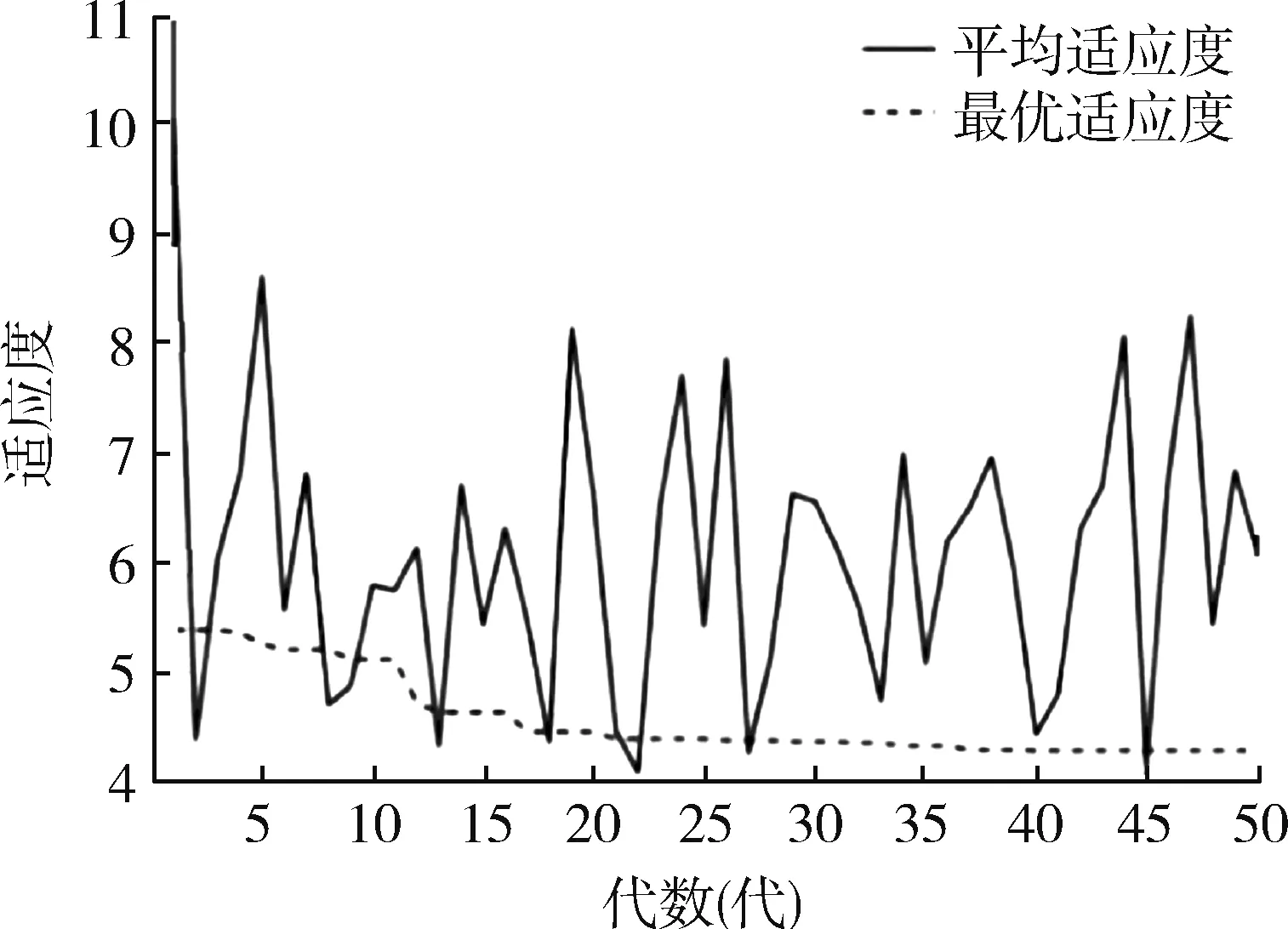
图6 GA-BP适应度随代数变化曲线Fig.6 GA-BP fitness cur ve with algebr a

图7 GA-小波-BP适应度随代数变化曲线Fig.7 GA-wavelet-BP fitness cur ve with algebr a

BP神经网络、GA-BP神经网络的拟合度曲线如图8，9所示。

图8 BP神经网络拟合度Fig.8 BP neural network fit degree

将271～283的13组数据作为测试样本，评估结果如图10和表5所示。

表5 BP神经网络、GA-BP神经网络、GA-小波-BP神经网络输出与真实值比较Table 5 BP neural network，GA-BP neural network，GA-wavelet-BP neural networ k output and real value compar ison

图10 评估结果对比图Fig.10 Comparison of evaluation results

为综合评价BP神经网络、GA-BP神经网络、GA-小波-BP神经网络的实际性能，采用平均绝对误差、最大绝对误差和最小绝对误差进行评判3种不同网络的性能，结果如表6所示。

表6 算法误差对比Table 6 Algorithm error comparison

GA-小波-BP神经网络的收敛速度、评估精度显著高于GA-BP和BP神经网络，测试样本平均绝对误差相比BP神经网络降低了45.8%，相比GA-BP神经网络降低了14.7%，最大和最小绝对误差远远小于BP和GA-BP神经网络的最大、最小误差，拟合度优于BP神经网络，迭代步数少，网络收敛快，避免了局部极小值和局部收敛问题，降低了平均误差，提高了评估精度。

图9 GA-BP神经网络的拟合度Fig.9 The fit of GA-BP neural network

4 结束语

本文利用粗糙集主分量约简算法对维修记录的冗余属性进行了约简，提高了网络的性能。提出了一种基于GA-小波-BP神经网络维修能力评估方法，通过某维修企业近4年的维修数据证实了本文提出评估模型的有效性和准确性，为进行装备维修能力评估提供了一定的方法借鉴。