混沌Yang系统的Hopf分岔分析与控制

周六圆， 崔 岩， 赵少卿， 卢晨晖

(上海工程技术大学 机械工程学院， 上海 201620)

0 引 言

混沌系统广泛存在于自然科学和人文科学领域[1]。1963年，Lorez[2-3]混沌模型的提出，证实了在混沌系统中，即使很小的扰动也会导致巨大的无法预测的变化，并且Lorenz在演讲中用著名的“蝴蝶效应”阐述了这一理论。著名数学家Smale对结果稳定性做了深入研究，引出了拓扑马蹄理论，随后混沌理论进入了蓬勃发展的时期[4]，一系列混沌模型也被研究人员发现，如Chen系统、Lü系统、Chua系统等[5—8]。近十年来，混沌系统设计、动力学分析、Hopf分岔、混沌控制和反控制、时滞系统分析等混沌研究不断发展，很多学者从各种自然现象和非线性的工程实际中抽象出各类混沌系统，使得混沌理论学说在迈向实际应用的过程中更进一步。在混沌理论应用过程中，时滞因素的作用不可忽视，Mackey 和 Glass 首先发现混沌现象存在于时滞系统中[9—12]。2015年，蔡萍[13]分析非线性动力系统的分岔理论，丰富和完善了Hopf分岔理论；魏朝颖等[14]通过周期函数正交性方法,分析了具有离散时滞的单种群模型Hopf分支周期解问题,并由此给出了τ0在分支周期解存在的充分条件；孙观等[15]通过对时滞类Lü系统的分析得出系统达到稳定时的时滞参数；陈立林等[16]在原Rössler系统基础上增加了时滞项，运用变量延时反馈法对Rössler混沌系统进行控制。

Yang系统是具有两个非线性项的类Lorenz 新型混沌系统[17]，本文在混沌Yang系统的基础上提出一种单时滞类Yang系统[18]，首先分析时滞系统的动力学特征，并结合计算得出单时滞Yang系统的时滞参数，明确系统发生Hopf分岔的条件；然后以此为基础对该系统采取线性状态反馈控制，对系统的分岔发生时间进行提前和滞后，由此控制分岔发生的时间，扩大系统的应用范围，实现对该时滞系统的有效控制；最后用MATLAB软件仿真验证理论结果的正确性。

1 时滞系统分析

1.1 单时滞混沌Yang系统稳定性分析

混沌Yang系统描述为

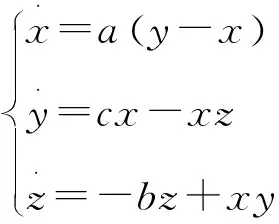
其中，a，b，c均为常数，当a=35，b=3，c=35时，混沌Yang系统存在混沌吸引子(图1)。

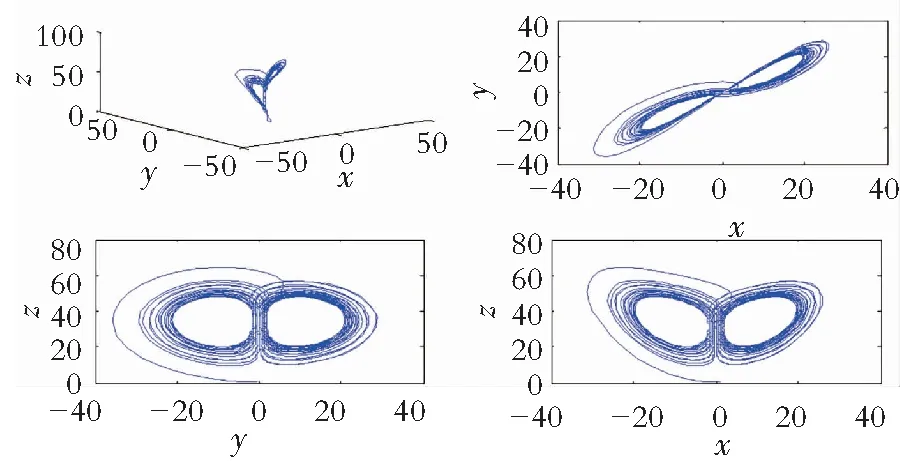
图1 Yang系统混沌吸引子图像

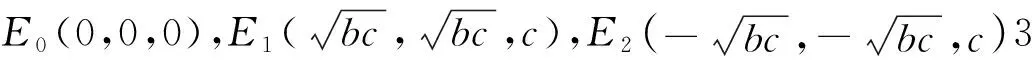
在研究Yang系统的稳定性问题时，本文提出了一种单时滞Yang系统。通过对单时滞Yang系统的平衡点稳定性分析和Hopf时滞分岔参数的分析研究，验证了单时滞Yang系统Hopf分岔的存在性。

在Yang系统的第二个方程上添加时滞项，方程描述为

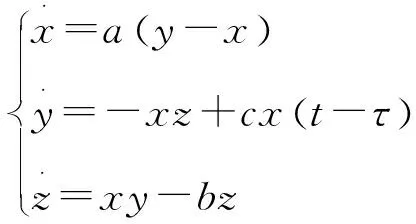
这里仅对平衡点E0(0,0,0)进行分析，其余平衡点分析相同。时滞系统在平衡点E0(0,0,0)处的线性化方程为

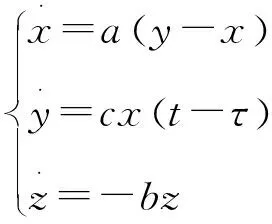
(3)

对应的Jacobi矩阵为

特征方程如下：

λ3+(a+b)λ2+abλ-(acλ+abc)e-λτ=0

令p1=a+b,p2=ab,p3=ac,p4=abc,得

λ3+p1λ2+p2λ-(p3λ+p4)e-λτ=0

(1)

当时滞参数τ=0时，有

λ3+p1λ2+(p2-p3)λ-p4=0

若特征方程所有的特征根均有复实部，根据Routh-Hurwitz判据可知，满足p1>0,p4<0,p1(p2-p3)+p4>0,对应参数代入式(1)可知条件满足，时滞系统在平衡点处是局部渐进稳定的。

1.2 Hopf 分岔分析

时滞参数τ>0，λ=±iω(ω>0)时，代入式(1)得

-iω3-p1ω2+p2iω(p3iω+p4)(cosωτ-i sinωτ)=0

令实数和虚数分别等于零，得

(2)

移项，平方相加：

(3)

令ω2=ξ,有

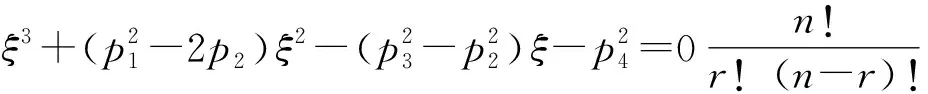
(4)

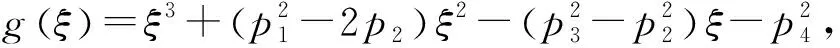
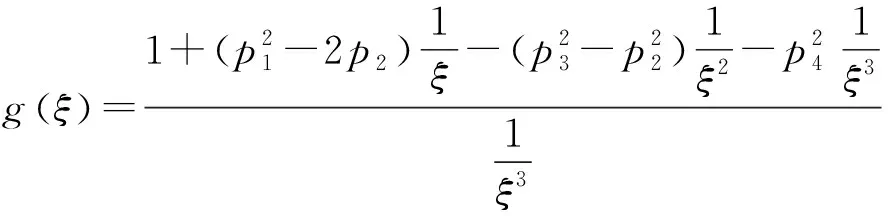
设ω0为式(3)的一个正实根，±iω0是一对纯虚根,代入式(2)得

再将ω=ω0代入式(11)，可得时滞参数τ：

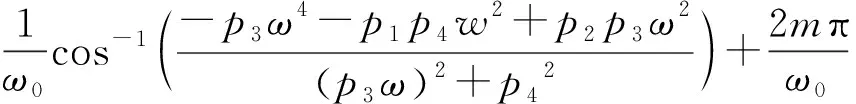
m=0,1,2,…

令(ω0，τn)为式(1)的解，当τ0是该式的最小时滞参数时，得出定理1。

定理1方程的特征根为λ(τ)=α(τ)+iω(τ)，λ=±iω0是一对共轭的纯虚根，使得α(τk)=0,ω(τn)=ω0。

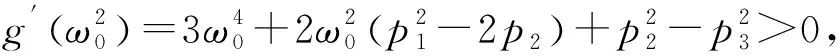
证明对于式(1)，两边求导可得

(5)

由式(1)可得

λ3+p1λ2+p2λ=(p3λ+p4)e-λτ

(6)

式(6)代入(5)中,可得

则有

时滞参数τ=τn时，时滞方程存在特征根，特征根为iω0，代入方程得λ3+p1λ2+p2λ-(p3λ+p4)e-λτ=0， 又e-iω0τ=(cosω0τ-isinω0τ)=0，|e-ω0τ|=1，方程两边取绝对值：

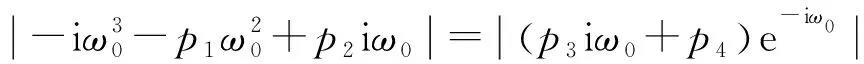
(7)

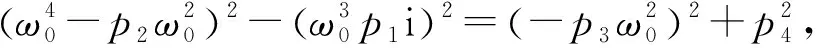
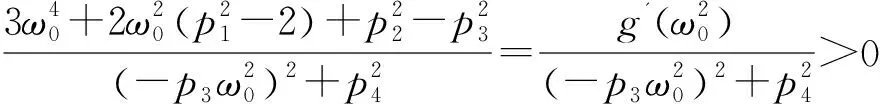
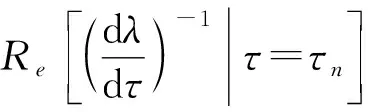
根据命题(1)与Hopf分岔可得下面结论：

(1) 当τ∈[0，τn)时，时滞系统在平衡点E0(0,0,0)处是趋向稳定的；

(2) 当τ=τn时，时滞系统在平衡点E0(0,0,0)处分岔已经产生，并存在极限环；

(3) 当τ>τn时，时滞系统在平衡点E0(0,0,0)的状态不稳定且存在较为稳定的极限环。

1.3 数值仿真分析

Yang系统的参数a>0,b>0,c<0，取a=8,b=2,c=-1,此时该系统为

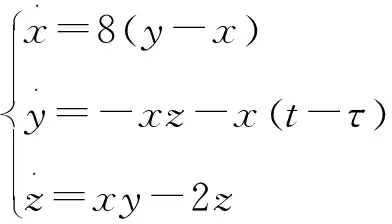
(8)

可得ω0=0.992 4，再将ω0代入到式(8)中，得τk=1.428 5，有如下结论：

(1) 当τ∈[0，1.428 5)时，系统在平衡点E0(0,0,0)是逐渐稳定状态；

(2) 当τ=1.428 5时，系统在平衡点E0(0,0,0)处产生分岔，并出现极限环；

(3) 当τ>1.428 5+kπ时，系统在平衡点E0(0,0,0)不稳定但存在较为稳定的极限环，此时发生的为超临界Hopf分岔。

当时滞参数τ取不同值时，Matlab仿真得到的结论如下：

(a) 当τ∈[0，1.428 5)时，图2给出了当时滞系数τ=1.400时系统时间序列，从图中可以观察到：系统的状态变量x,y,z在较短的时间内趋近平衡点，因此系统在平衡点E0(0,0,0)处是稳定的，结论(1)得证。

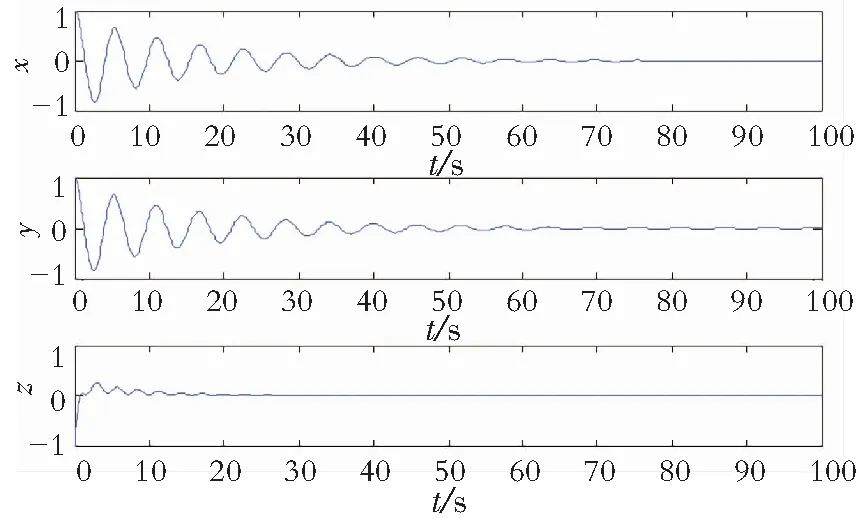
图2 τ=1.400时系统时间序列

(b) 当τ=1.428 5时，图3给出了系统时间序列和极限环，此时系统所经历的历程与τ∈[0，1.428 5)类似，但此时该系统已经产生极限环，结论(2)得证。

(c) 当τ>1.428 5时，图4给出了当时滞系数τ=1.428 5时，系统的局步分岔图，其状态变量x,y,z随时间t的增大而进入稳定的震荡，即产生极限环，说明系统在平衡点E0(0,0,0)处是不稳定的，此时该系统极限环的状态稳定性较好，结论(3)得证。

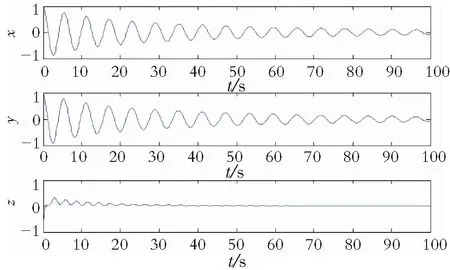
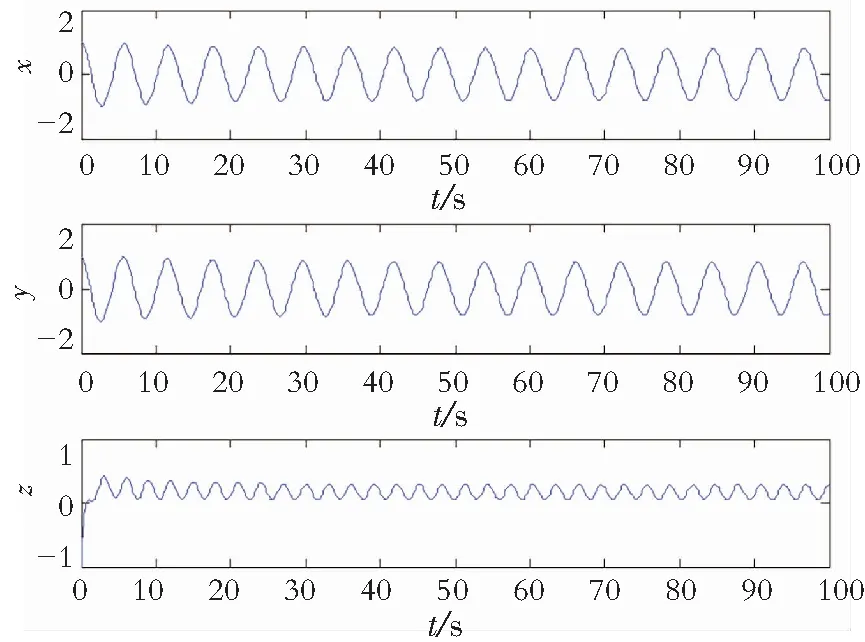
(a) 时间系列

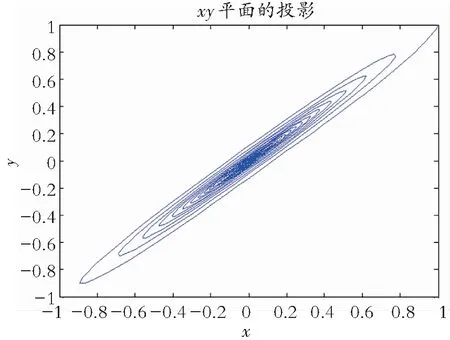
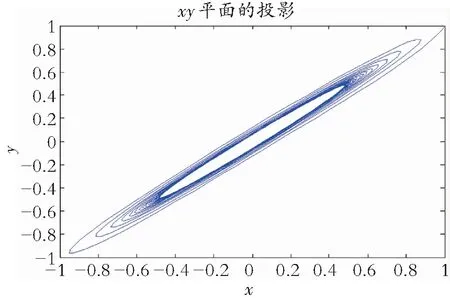
(b) 极限环图3 时滞系数τ=1.428 5时系统时间序列和极限环

图4为系统时滞参数τ的局部分岔图，当τ=1.428 5时，时滞系统到达分岔临界点。

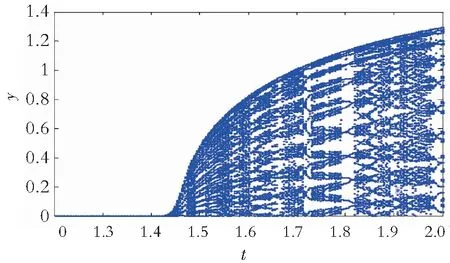
图4 时滞Yang 系统局部分岔图

2 分岔控制

2.1 时滞系统分岔控制

对于该系统,参数取a=8，b=3，c=-1,此系统在τ=1.425 8处产生分岔。设计线性状态反馈控制对系统的状态变量进行控制，可改变其分岔状态，并对极限环的幅值也会有一定的影响。在实际生产中，可采用阻尼减振器等实现该线性控制器的功能，对于该系统，可以采用线性控制k(x-p),其中k为控制参数，此处的p为对应于平衡点处的坐标值，由于其对应的平衡点为E0(0,0,0),因此p=0。线性控制项k(x-p)可添加在系统的第二个方程中，则整个系统可变为

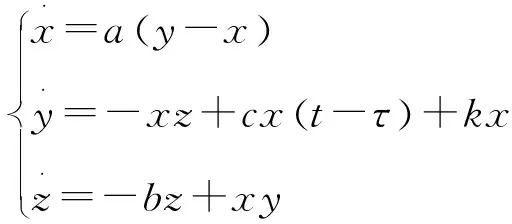
(9)

将系统线性化得

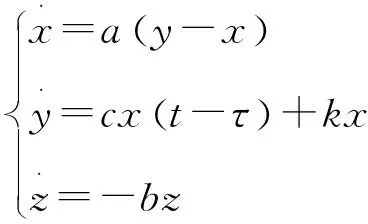
(10)

受控系统的Jacobi矩阵为

则线性部分的特征矩阵为

对于该系统的分岔控制，若仅考虑虚根，则该系统的特征方程为λ2+aλ-ace-λτ-ak=0，将λ=±iω0代入该特征方程，化简后可得如下方程组:

根据三角恒等变换可得受控系统的时滞参数为

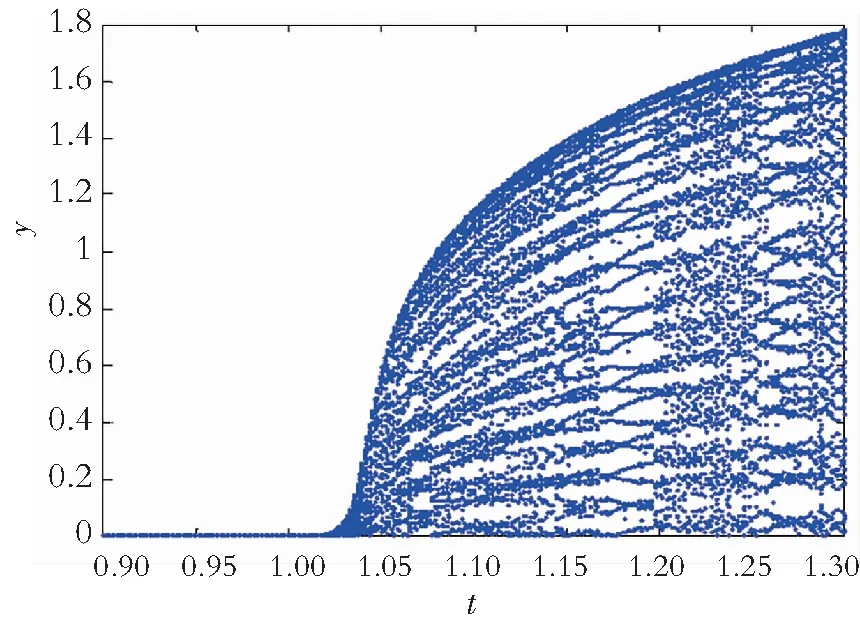
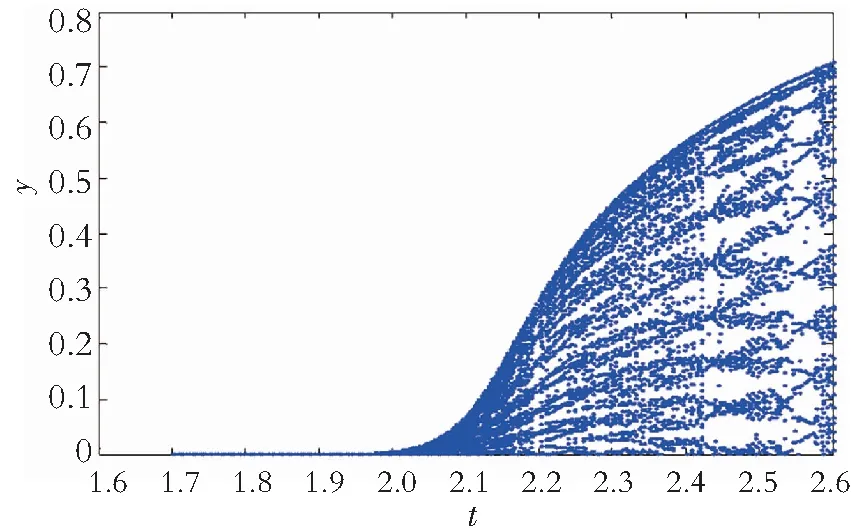
在调节整个系统的分岔参数过程中，当0

2.2 仿真结果

对于该受控时滞系统，在数值仿真计算中采用四阶龙格-库塔验证以下结果：在控制参数k满足取值范围情况下，改变其值可以提前或滞后分岔的产生。

(1) 取k=0.75，对时滞系统进行控制后，该系统的分岔参数有所改变，图5给出了受控时滞系统的分岔图以及时间序列情况。可以看出分岔点由原来的1.428 5提前至1.250 5，时滞参数τ=1.428 5时,原本趋近平衡点的系统状态变量x,y,z也开始变得震荡起来并逐渐远离平衡点，同时整个分岔系统的幅值增加。

(a) Hopf分岔图

(2) 取k=-0.75，由图6可以看出分岔点由原来的1.428 5滞后到1.943 5，时滞参数τ=1.428 5时，系统的状态变量x,y,z在更短的时间内趋近于平衡点，整个分岔过程的幅值下降。

(a) Hopf分岔图

以上仿真表明:可以添加适当的控制器对时滞系统进行提前或滞后控制，并且该受控系统的整体幅值与原系统相比，有较大变化。

3 结束语

在对单时滞Yang系统的研究中，给出了时滞系统局部保持稳定和出现Hopf分岔的充分条件，得到了时滞参数τ∈[0，1.428 5)时，系统在短时间内趋于稳定；当τ=1.428 5时，系统产生分岔并存在较稳定的极限环；当τ>1.428 5时，时滞系统状态不稳定。对时滞混沌系统的线性反馈控制研究显示：在适当的控制参数调节下，可以成功地将时滞系统分岔点提前或者滞后。通过MATLAB软件的仿真实验验证了分析的正确性。