一类带Kirchhoff扰动项拟线性Schrödinger方程非平凡解的存在性

李国发

（曲靖师范学院 数学与统计学院，云南 曲靖 655011）

本文将研究一类如下形式的带Kirchhoff扰动项一般对偶拟线性薛定谔(Schrödinger)方程非平凡解的存在性

其中位势函数V∈C(ℝ3,ℝ)和函数g∈C1(ℝ,ℝ+)满足如下条件

(V1)V(x)≥V0＞0,∀x∈ℝ3。

(V2)对任意的M＞0有meas({x∈ℝ3:V(x)≤M})＜+∞，这里meas为ℝ3中的Lebesgue测度。

(g1)g是偶函数，对任意的

当b=0，方程（1）变为如下拟线性Schrödinger方程

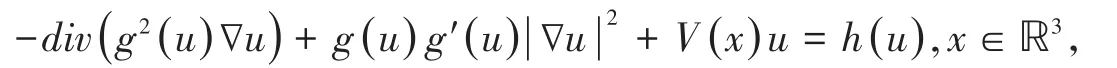
此方程有非常丰富的物理背景，函数g的不同可以导出不同的物理现象[1，2]。当g(t)=1时，方程（1）可以化为如下的Kirchhoff方程

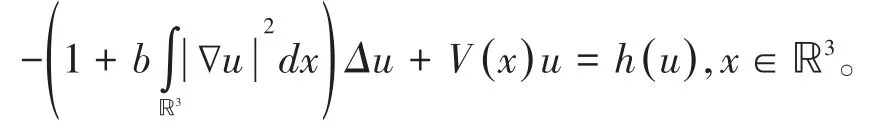
从数学的角度研究以上问题具有重要的理论意义，也是目前研究的热点问题，发表了许多重要结果。函数g在讨论解的存在性过程中带来了困难，人们通常需要用对偶变换技巧来克服此困难，即处理函数g，我们将此函数称为对偶变换函数，我们在文献[4]中提出了条件(g1)，有许多特殊的函数满足条件(g1)[3]，这样就推广许多文献中的对偶变换函数。本文将利用变分方法讨论在条件(g1)之下方程驻波解的存在性，本文中我们假设非线性项h∈C(ℝ,ℝ)满足：

(h3)0＜4H(t)≤h(t)t,∀t∈ℝ。

在如上的条件中，我们称非线性项h在无穷远处满足3-超线性增长，据我们所知，对此问题的研究结果还很少，以下是本文的结果：

定理1 假设(V1)，(V2)，(g1)，(h1)-(h3)成立，则方程（1）有一非平凡解。

注记：有许多函数满足条件(h1)-(h3)，例如h(t)=|t|q-2t,4＜q＜6,t∈ℝ。

本文中，我们将采用如下记号：‖u‖q(1＜q≤∞)记为Lebesgue空间Lq(ℝN)中的标准范数，→记为强收敛，on(1)是n→∞时的无穷小量，C,C0,C1,…记为正常数。

1 变分框架

我们定义如下空间

并赋予范数

由条件(V1)和(V2)可知此范数与标准的空间H1(ℝ3)的范数等价。

我们注意到方程（1）的能量泛函为

泛函I(u)可转化为

泛函J(v)为如下方程的能量泛函

下面给出函数g的一个性质。

引理1[4]假设(g1)成立，则对偶变换函数g(t),满足如下性质：

由引理1，泛函J在空间X中是良定义的，直接计算可知对所有的v,ψ∈X,J∈C1且

标准的讨论可知v∈X是方程（3）的一个弱解当且仅当如果u∈X是泛函I的一个临界点，此临界点即为方程（1）的弱解，具体的讨论过程可参见文献[5]。

2 定理的证明

我们将利用山路定理证明定理1，首先证明泛函J满足山路几何，获得(PS)c序列{vn}，其次证明(PS)c序列在X中有界，最后证明{vn}强收敛。

引理2 假设条件(V1)，(V2)，(g1)，(h1)和(h2)成立，则存在ρ,α＞0，使得J(v) ≥α,∀v:‖v‖=ρ。

证明：由条件(h1)，(h2)，存在Cε＞ 0使得