基于模糊大脑情感学习的神经网络控制器研究

郑泛舟

（湄洲湾职业技术学院 信息工程系，福建 莆田 351119）

神经网络控制器在一些特定条件下，例如在有界的跟踪误差和补偿控制器的存在下，能够保证闭环性能[1]。此外，通过建立连续时间和离散时间的神经网络校正算法使得神经网络权值易于初始化，神经网络能够实时在线学习，避免了需要预先离线学习；与传统的自适应控制相比，神经网络控制器不需要建立回归矩阵；并且，将Lyapunov稳定性判据引入，保证了跟踪误差和权值估计误差都是有界的，这大大保证了神经网络控制器的稳定性。因此，神经网络控制器一直是智能控制领域中的研究热点，不但在人工智能领域，也在自动控制领域都受到了极大的关注。

当今智能控制领域学者的很多工作受到了人脑结构的启发，尝试建立不同的神经网络模型来提高神经网络控制器的效率，例如，Moren和Balkenius[2]的大脑情感学习模型网络（Brain Emo‑tional Learning，BEL）就是此类的一项开创性的工作。该网络在数学上模拟了杏仁核和大脑中相关部分的情绪活动。BEL网络由四个子系统组成：丘脑、感觉皮层、杏仁核和眶额皮质。输入信号从丘脑进入，通过应用非线性映射后，被映射到感觉皮层。杏仁核通过感觉皮层接收精确和间接的信号，并且杏仁核直接从丘脑接收不精确的信号，从而产生兴奋信号。除了丘脑输入外，眶额皮质的连接也是一样的。它抑制杏仁核不匹配的部分激发信号产生网络输出。杏仁核和眶额皮质也会接收到一个外部增强信号，以调整它们的权重，从而适当地执行信号传递任务[3]。

大脑情感学习网络模型作为一种先进学习型结构迅速进入控制和决策领域，对实际的控制过程进行系统建模，参数估计，甚至用作控制器。不少研究者将大脑情感学习网络用于自适应控制系统中，验证这种网络在线性和非线性系统的控制系统中的表现[3-4]。此外，比较典型的研究还有Debnath等人利用大脑情感学习网络优秀的非线性特点，在模拟环境中对四罐系统进行了模拟，收到了较好的效果[5]。Deshti等人还提出了将大脑情感学习网络用在流动非线性、内部摩擦和噪声情况下对电动液压伺服系统进行速度控制[6]。还有不少研究工作尝试使用大脑情感学习网络控制不同类型的机械臂和移动型机器人[7-9]。

从现有的研究中发现大脑情感学习在非线性函数拟合的能力可以引入模糊推理系统。但现有的研究中对于模糊推理机制在大脑情感学习的改进和应用还比较有限。因此，本文对一种模糊大脑情感学习神经网络网络模型进行了研究与实现，为了提高模糊大脑情感学习神经网络网络的控制表现，将其嵌入到带有滑模面的前馈型自适应控制器中，并分别在混动模型和六足机器人的模拟环境中进行验证。实验结果表明，引入模糊推理机制的大脑情感学习网络具有较好的非线性拟合能力和应对控制中的扰动抑制能力。

1 模糊大脑情感学习网络的基本结构

模糊大脑情感学习网络的结构如图1所示，模糊大脑情感学习网络由眶额皮层通道和杏仁核通道组成。眶额皮层通道是一个情感网络，杏仁核通道是一个感官网络。一种单输出的模糊大脑情感学习网络可以由如下表示：

图1 大脑情感学习控制器网络结构图

其中i=1,2,…,m;并且，j=1,2,…,n.i是系统输入的个数；j是隐含神经元的个数，a是杏仁核的输出量，o是眶额皮层输出量。每个隐含神经元的传递函数如下：

其中sij是高斯函数的输出，Ii是系统输入，ζij是均值，是方差。此外，基于两个模糊规则库的大脑情感模型网络推理系统被用于感觉神经网络的模糊杏仁核系统，模糊规则库则表示为：

如果Ii是λ1j并且Ii是λ2j,…,那么a=vij，

如果Ii是λ1j并且Ii是λ2j,…,那么o=wij，

其中vij和wij分别为两个通道的权重。权重的更新由下式给出：

其中α和β是学习率，uBELC是网络输出，dj的参数调整如下：

其中bi和c是增益参数，通常在实际控制中根据经验确定。

图2给出了基于神经网络的控制器结构图，它包括了被控对象基于神经网络的控制器模块。误差与其一阶导数的组合误差被输入基于神经网络的控制器中。控制器由一个模糊大脑情感学习神经网络uFBEL和一个鲁棒控制器组成ur；其中模糊大脑情感学习神经网络作为主控制器，接收组合误差输入，输出为控制量；而鲁棒控制器作为一个辅助控制器，为弥补模糊大脑情感学习神经网络逼近理想的系统动力学过程中的近似误差而设计；模糊大脑情感学习神经网络的输出和鲁棒控制器的输出组合到一起作为整体控制器的输出u，其定义为u=uFBELC+ur。这里，鲁棒控制器ur的定义如下：

图2 模糊大脑情感学习网络控制器结构图

其中，R=diag(r1,r2,…,rm)和I是一个统一矩阵；s(,t)是一个滑膜平面。

2 仿真实验

为了验证模糊大脑情感学习网络控制系统的有效性，在实验中使用该控制器对Duffing-Hol‑mes混沌系统和六足机器人系统进行控制。为了比较所提出的控制系统的性能，我们与其它两种控制模型做了比较。两种比较模型是：传统的PID控制模型和模糊小脑控制器网络建立的控制器。

2.1 Duffing-Holmes混沌模型与实验设置

Duffing-Holmes混沌系统是典型的复杂不确定非线性系统，该混沌系统由两个子系统组成：（1）驱动子系统和（2）响应子系统。这两个子系统的定义如下：

（1）驱动子系统表示为：

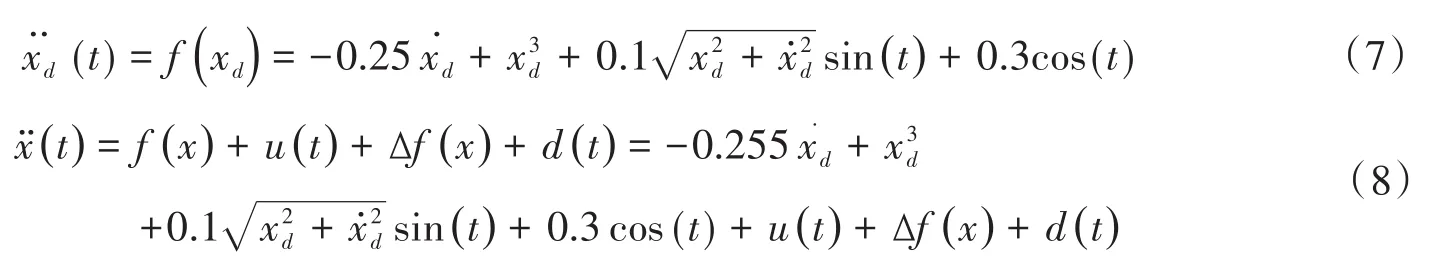
其中xd和x分别代表驱动系统和响应系统的系统状态，u表示输入，Δf(x)表示未知不确定项，d(t)是外部扰动。本次实验中，系统的初值为：；滑动表面设计为：

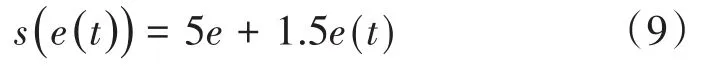
2.2 实验结果

三个控制系统的仿真结果如图3所示，红色实线表示驱动系统的参考轨迹；黑色实线、绿色实线、蓝色实线分别表示PID，FCMAC（模糊小脑控制器网络）和FBEL（模糊大脑情感学习网络）控制系统生成的跟踪轨迹。在图3中，由三个控制系统生成的所有轨迹都可以成功地跟踪混沌轨迹。但模糊大脑情感学习网络控制系统的轨迹比其他的控制系统更早的到达参考点。

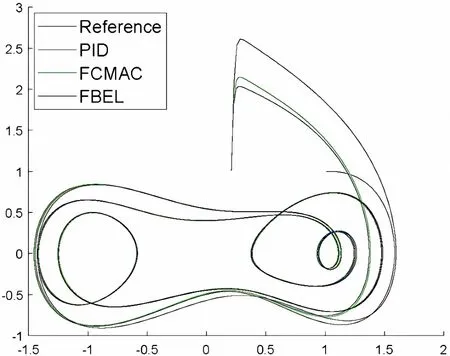
图3 混动系统轨迹跟踪图

完整的跟踪响应如图4(a)所示，在该图中，所有三个控制系统都可以很好地跟上追踪目标，性能差异仅在跟踪开始时存在。因此，图4(b)中展示了前两秒的跟踪性能。从图中可以看出，模糊大脑情感学习网络实现了良好的追踪性能，而且在进行了一段调整后，模糊大脑情感学习网络可以快速捕捉参考轨迹，并紧跟目标。相反，PID和模糊小脑控制器网络的轨迹需要更长的时间才能逼近目标轨迹。

图4(c)显示了三个控制系统从0秒到50秒的跟踪误差，图4(d)显示了在前5秒期间的跟踪误差。在这两个子图可以看出，所有控制系统都具有稳定的性能，但是模糊大脑情感学习网络控制系收敛更快。

图4 xd与x的轨迹图

表1给出了所有控制器的跟踪误差的累积RMSE值，从表中可见，PID和模糊小脑控制器网络的性能非常接近，而模糊大脑情感学习网络明显优于上述的两个控制器。因此由该实验可以得出结论，基于模糊大脑情感学习网络的控制系统优于其他的控制系统。

表1 三种控制器在混动系统中累积RMSE表现

2.3 六关节双足行走机器人

图5给出了一个六关节的双足行走机器人示意图。该机器人的数学模型表示如下：

图5 六关节的双足行走机器人示意图

在上述表达式中，其中b=0.145m，其余各个参数的具体值如表2所示，其中n的取值范围为1到6。

表2 六关节的双足行走机器人的参数设置

2.4 实验结果

在六关节双足机器人的仿真实验中，我们计算了三种控制器在各个关节的累积误差，并汇总在表3中。可以看到PID控制器在关节4中的表现最好，其次是FCMAC控制器，而FBEL控制器在关节四种的精度没有超过前两种。FCMAC控制器在关节6中表现的最好，而PID与FBEL的精度稍差，但是差别不会太大。相比之下，FBEL控制器在剩下的4个关节中达到了最好的控制效果，且明显超出另外两种控制器的幅度。实验结果表明：FBEL在更复杂的非线性系统的控制中，能够达到总体比较优势的效果。

表3 三种控制器在六足机器人中各关节累积RMSE表现

3 结论

本研究实现了一种引入模糊推理机制的大脑情感学习神经网络，并在一种混沌系统中验证了它的有效性。实验过程与实验结果表明，这种新型的网络不需要通过反向传播方法，仅仅依靠大脑情感学习就可以很好的实现系统的稳定。因此，这种网络对实现轻量化的网络控制器具有很好的应用意义。在未来的工作中，可以将这种网络控制器推广到不同的机器人实际控制器中，实现对机器人系统的实时与高精度控制。