一个函数应用“对数求导法”求导过程的探析

杨 雄 周立芬

（1.娄底职业技术学院，湖南 娄底 417000；2.邵阳县第一高级中学，湖南 邵阳 422100）

微积分是高等数学的重要内容，其中求导是微积分的主要内容之一，并且对函数的求导的方法灵活多样——定义求导、求导公式、求导的四则运算法则、复合函数求导和反函数求导等。若一个函数是幂函数、指数函数及幂指函数或由这几个函数组合成的结构形式，并且函数式中又有乘、除、乘方、开方等运算，则采用前面提到的方法求导，会比较困难，进而大部分教材介绍了“对数求导法”。对数求导法是一种很方便求函数导数的方法，取对数的运算可将幂函数、指数函数及幂指函数运算降格成为乘法运算或除法运算降格为加法或减法运算，使求导运算量大为减少。其采用的原理是对数运算和复合函数求导法则，适用的范围是函数由乘积形式、商的形式、根式、幂的形式、指数形式或幂指函数形式等构成的复合函数。可在应用对数求导法时，有时忽略了对数的真数要大于零的条件，细心的同学会提出问题，对于函数的定义域范围内，有时函数值小于零或等零时，函数等式两边取对数是否合理。鉴于此，从教材的案例出发，通过分析存在的问题，提出解决问题的方法，并且探讨对数求导法合理的构思，最后应用实际案例给出对数求导法的严谨解题过程。当然对数求导法在幂指函数求导中应用很广，值得探索，可以参考其他的书籍[1]和文献[2-3]，这里只探讨以下案例1类型的函数求导过程。

1 教材中案例分析

大部分教材在求导章节中会有案例1的举例，有假设x＞4的，有没有考虑x取值范围的[4]，也有考虑x的取值范围的，但没有考虑端点的导数[5]，教师上课时甚至说不用考虑x的取值范围。进而导致求导的过程不能完全说服学生，因此我们在讲解求导的过程时要考虑自变量的取值范围。

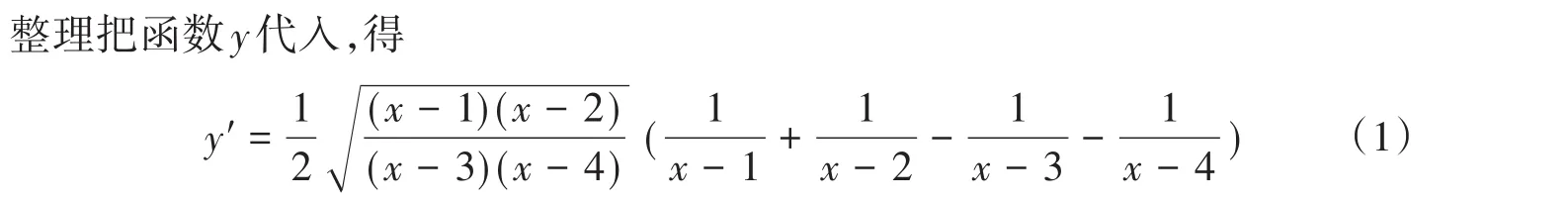
分析1：作出案例1函数的图像如图1所示，从图像上可以看出函数的定义域是(-∞,1]∪[2,3)∪(4,+∞)，若不考虑定义域，直接求导，相当于没有考虑导数不存在的点，即无定义点、左右导数存在但不相等点、左右导数至少一个不存在点的导数是不存在的。若定义x＞4，则缩小函数的实际定义域，求出来的导数很难具有说服力。因此从图1可以看出，求导时要分段进行，并且要考虑端点的导数问题。

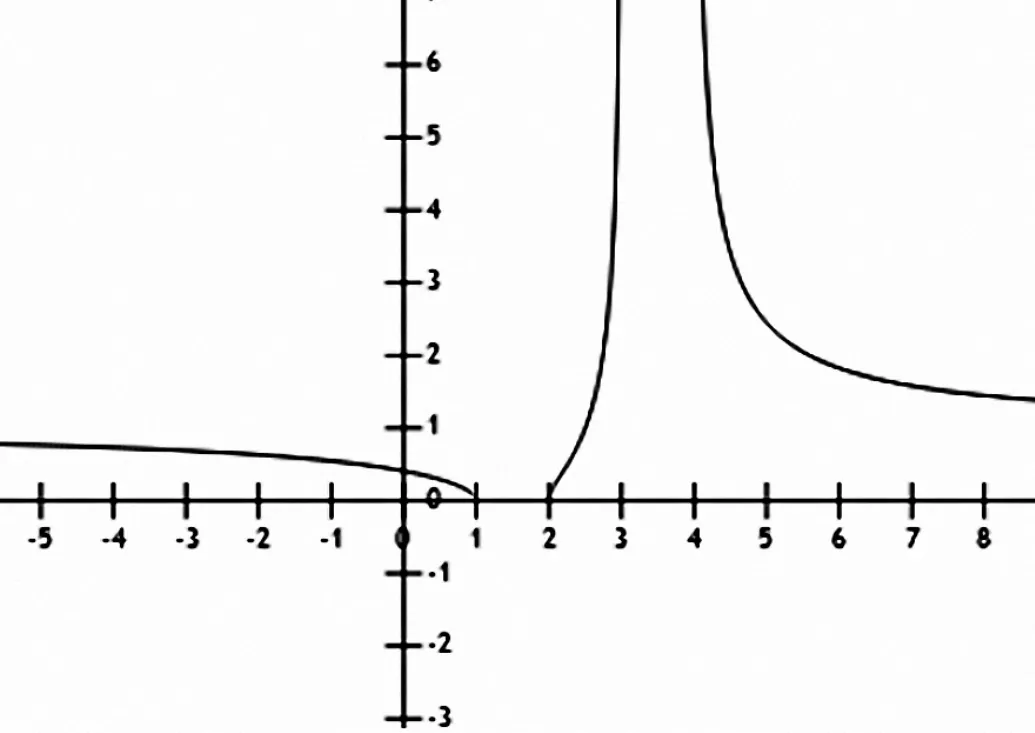
图1 案例1函数的图像

分析2：案例1利用对数求导的计算过程是方便快捷，并易学易懂，但是解题过程不太严谨，如x＜1时，ln(x-1)等是没有意义的，可x＜1在原函数的定义域内，即计算过程没有考虑到函数的定义域及对数真数要求大于0的情况，正确的求解应考虑定义域(-∞,1]∪[2,3)∪(4,+∞)内部点及x=1和2两个端点的导数问题，进而应该分步对此函数进行求导。

（ⅰ）应用左右导数的定义判断x=1和x=2是否可导，则有

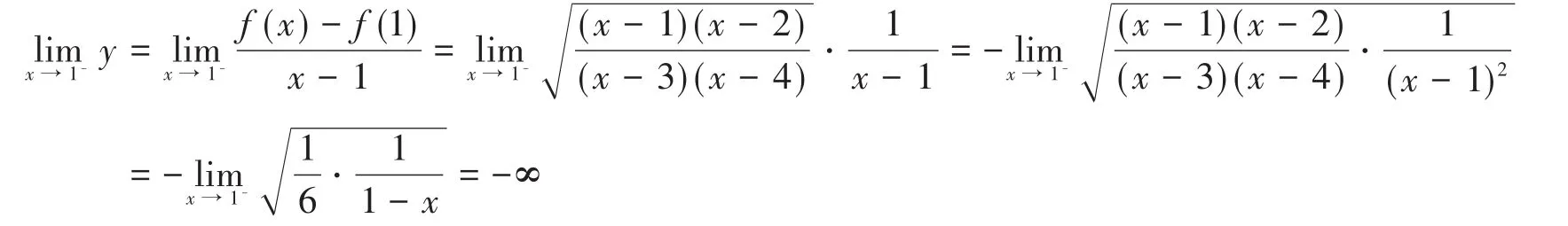
所以f＇(1)不存在，同理可求x=2右导数不存在，进而f＇(2)不存在。

（ⅱ）当x∈(-∞,1)时，原式可变为

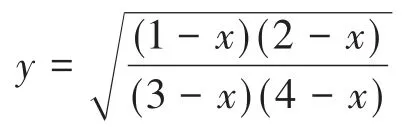
对等式两边同时取自然对数和求导，并进行整理，即可得（1）式。

（ⅲ）当x∈(2,3)时，原式可变为

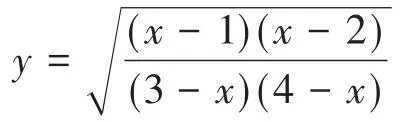
对等式两边同时取自然对数和求导，并进行整理，即可得（1）式。

（ⅳ）当x∈(4,+∞)，（1）式的求解过程即可得导数。

综上可得，x∈(-∞,1)∪(2,3)∪(4,+∞)函数可导，且导数为

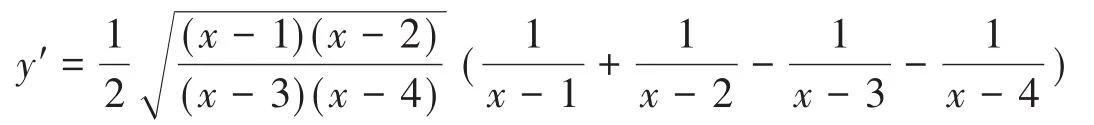
当x=1或x=2时，函数的导数不存在。

2 对数求导法深入探讨

2.1 对数求导法的一般步骤

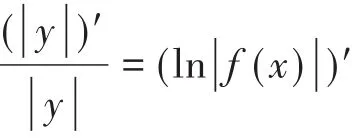
2.2 对数求导法合理性的深入探索

对案例1是否存在方法使其在计算过程中更合理，先看y=ln||x,(x≠0)的导数

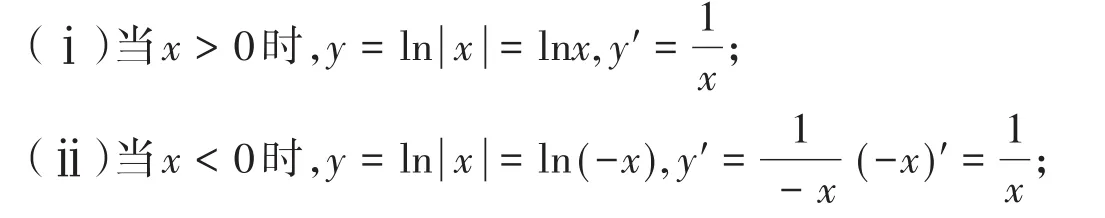
从上面的求导可知，y=ln|x|,(x≠0)与y=lnx,(x≠0)的求导结果是一致的，因此加绝对值对结果没有影响，虽然结果没有影响，但若不取绝对值，则求对数过程中，若自变量不大于0是没有意义的。

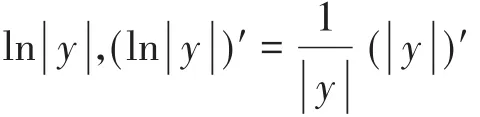
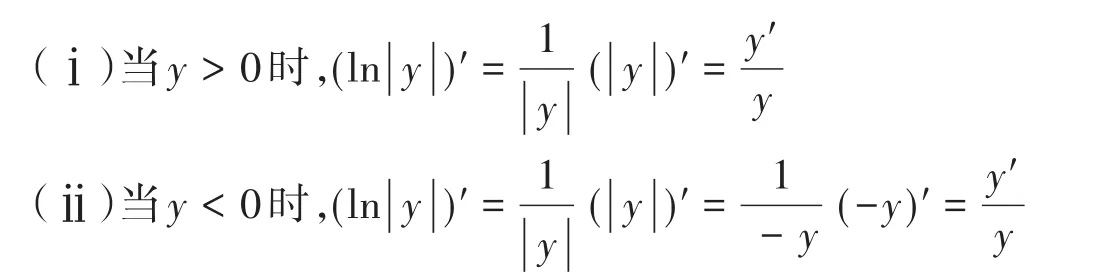
从上面的求导过程可知，不管函数f(x)是否为正还是为负，加不加绝对值都对求导结果没有任何影响，但从解题的严谨性看，在取对数前必须加绝对值，可取绝对值之后，问题又来了，在求解导数时，要去绝对值进行讨论，并且一些零点值要应用左右导数的定义进行求解，这样的求解导数是严谨的过程，如案例1的分析过程，可发现求导过程还是较复杂，那是否有办法避免去绝对值的讨论，是否有直接的方法求出零点的导数值，进而进一步思考可得出下列命题。

命题1：若有函数f(x)定义域内可导，当定义域包括端点时，端点的左导数或右导数存在，且f(x)≠ 0，则

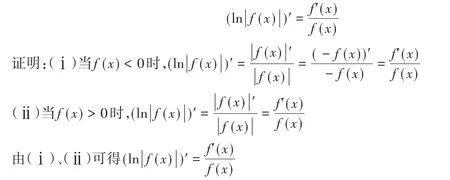
此命题可以在函数取绝对值之后取对数的求导过程中，避免分情况讨论，进而减少了许多计算过程，如案例1解题过程取对数时可转化为（2）式，再由命题1进行求解，则求解过程就严谨了。

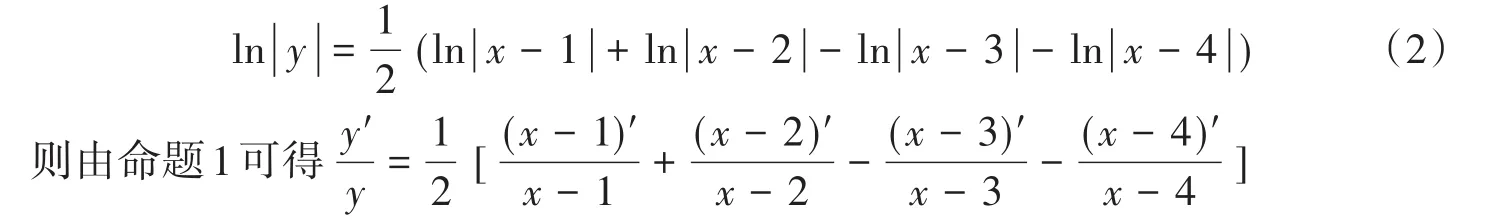
命题2：[6]设f(x)=(x-x0)aφ(x)，其中a为常数，f(x)在x0的领域u(x0)内仅有x0一个零点，φ(x)在u(x0)内连续且φ(x)≠ 0，则

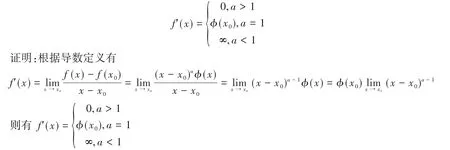
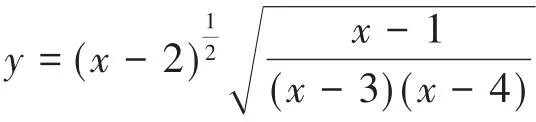
2.3 对“对数求导法”求导的推广

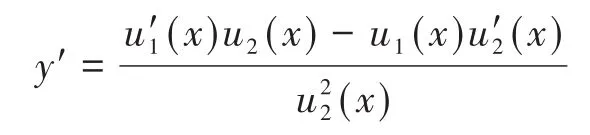
3 对数求导法合理性解题过程举例

函数乘积形式的求导，可以应用积的求导公式进行求解，但有些函数式，既有乘积又有幂及根式，如直接用积求导公式，运算过程复杂，只宜采用对数求导法，实质是通过对数运算把积式转化为和式，然后对和式进行求导，进而简化了积求导繁杂的过程。但在求对数时一定要考虑定义域范围内，取对数是否有意义。

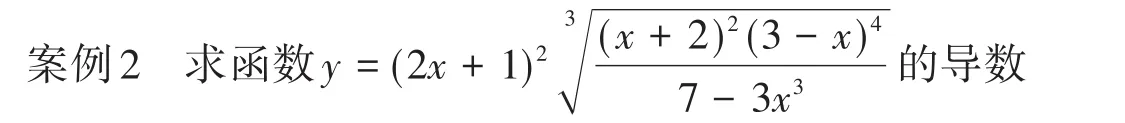
分析：这是乘积形式的求导，若直接应用公式求导，计算量大，并且不一定能求出导数，先用对数计算把乘积式转化为和式，当然应注意取对数前先取绝对值，因求导的函数可能取负值，只有取绝对值，才能保证函数定义域内取对数时，真数中的因式大于0，对数在有意义[7]，定义域一些特殊点取0时，可以根据命题2进行考虑，真数大于0的因式再根据命题1，即可完成求导。

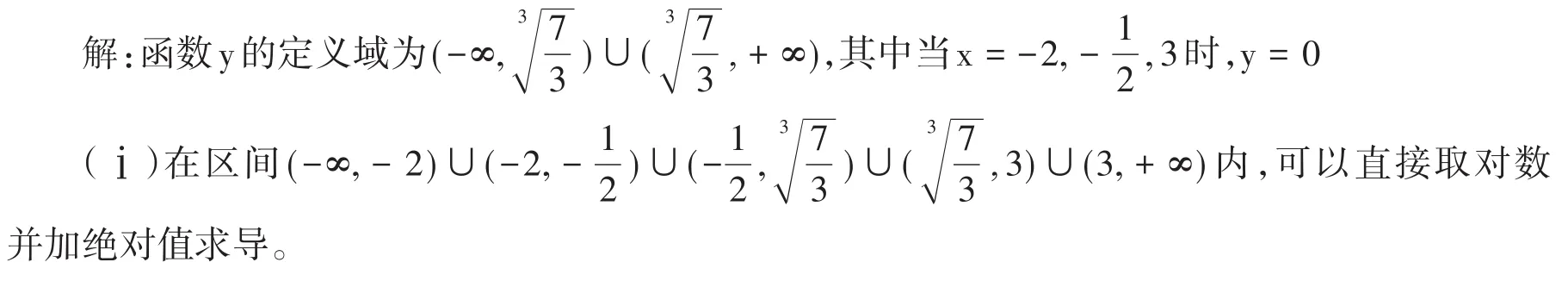
4 结论

本文从案例出发，发现应用对数求导法解题过程中，若不取绝对值，解题过程不够严谨，进而进行深入分析，得出对数求导过程中，等式两边取对数时是否加绝对值求导的结论是一致的，但解题过程中当函数值小于0或等于0做真数是无意义的，因此取对数应加绝对值，加绝对值后为了计算方便，进一步得出命题1，命题1避免了真数去绝对值的讨论。当然在函数的定义域的一些特殊点的函数值为0，取对数做真数也无意义，一般应用函数在某一点导数定义来求这些特殊点的导数或判断这些点的导数不存在，用导数的定义求导数，要用到极限的思想，计算量大，为计算的方便，进而得出了命题2，可以直接判断一些特殊点的导数不存在或直接求出这些点的导数值。对数求导法是一种常用的求导方法，但在求解问题中要认真考虑真数的取值范围。文章最后给出实际案例，运用对数求导法给出了严谨的解题过程，为教师教学和初学对数求导法的学生提供参考。