概率知识核心考点综合演练

■张 夏 刘中亮

一、选择题

1.下列命题中正确的是( )。

A.事件A发生的概率P(A)等于事件A发生的频率fn(A)

C.掷两枚质地均匀的硬币,事件A为“一枚正面朝上,一枚反面朝上”,事件B为“两枚都是正面朝上”,则P(A)=2P(B)

D.对于两个事件A,B,若P(A∪B)=P(A)+P(B),则事件A与B互斥

2.下列四个命题:①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件。其中正确命题的个数是( )。

A.1 B.2

C.3 D.4

3.(多选题)某次数学考试的一道多项选择题,要求是:“在每小题给出的四个选项中,全部选对的得5分,部分选对的得3分,有选错的得0 分。”已知某选择题的正确答案是C,D,且甲、乙、丙、丁四位同学都不会做,则下列表述正确的是( )。

4.(多选题)从集合A={-1,-3,2,4}中随机选取一个数记为a,从集合B={-5,1,4}中随机选取一个数记为b,则( )。

5.(多选题)利用简单随机抽样的方法抽查某工厂的100 件产品,其中一等品有20件,合格品有70件,其余为不合格品,现在这个工厂随机抽查一件产品,设事件A为“是一等品”,B为“是合格品”,C为“是不合格品”,则下列结果正确的是( )。

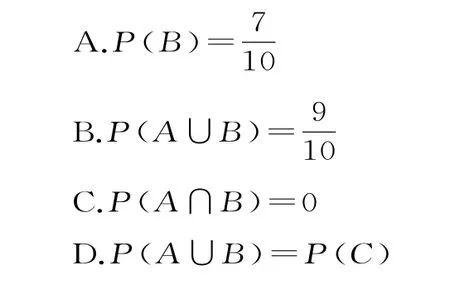
二、填空题

①A与D为对立事件;②B与C是互斥事件;③C与E是对立事件;④P(C∪E)=1;⑤P(B)=P(C)。

三、解答题

9.某服务电话,打进的电话响第1 声时被接的概率是0.1;响第2声时被接的概率是0.2;响第3声时被接的概率是0.3;响第4声时被接的概率是0.35。

(1)打进的电话在响5 声之前被接的概率是多少?

(2)打进的电话响4 声而不被接的概率是多少?

10.甲、乙两人参加普法知识竞赛,共有5题,选择题3个,判断题2个,甲、乙两人各抽一题。

(1)甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少?

(2)甲、乙两人中至少有一人抽到选择题的概率是多少?

11.A,B两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:

A组:10,11,12,13,14,15,16。

B组:12,13,15,16,17,14,a。

假设所有病人的康复时间互相独立,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙。

(1)求甲的康复时间不少于14 天的概率。

(2)如果a=25,求甲的康复时间比乙的康复时间长的概率。

(3)当a为何值时,A,B两组病人康复时间的方差相等? (结论不要求证明)

12.在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3 只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写着摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1 元钱。

(1)摸出的3个球为白球的概率是多少?

(2)摸出的3个球为2个黄球1个白球的概率是多少?

(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱。

一、选择题

,,,,

(3)把B组数据调整为a,12,13,14,15,16,17或12,13,14,15,16,17,a,可见当a=11或a=18时,与A组数据方差相等。(可利用方差公式加以证明,但本题不需要)