模型估计对序数响应轮廓控制图的影响
王志琼 李金梦 王 颖 马彦辉
天津理工大学管理学院,天津,300384
0 引言
统计过程控制(statistical process control,SPC)是一种将统计技术应用于过程监控的方法,该方法通过控制图等工具监控过程的稳定性,以确保最终产品的质量[1]。在实际中,某些产品或过程的质量特性需要用函数关系表示,如产品故障率与使用时间的关系,这种响应变量与一个或多个解释变量之间的函数关系称为轮廓(profile)[2]。对由一系列轮廓组成的时间序列数据进行监控被称为轮廓监控[3]。根据轮廓响应变量的性质,轮廓可分为两种类型:一种是具有数值响应变量的轮廓,另一种是响应变量为属性(计数或分类)数据的轮廓。对于第二种轮廓,大部分监控方法没有考虑响应属性之间的序数信息(例如,好、中和差),而这些信息对构建控制方案具有重要的作用。NOOROSSANA等[4]通过使用序数逻辑回归拟合轮廓模型,提出了4种方法来监控序数轮廓,这是对序数轮廓的首次研究。HAKIMI等[5]使用序数列联表拟合序数变量之间的关系,并提出了一种基于序数正态统计量的控制图,用于监控序数对数线性模型。DING等[6]假设存在一个潜在的连续变量决定响应变量的水平,提出了一种新的控制方案,用于监控参数回归模型。本文针对响应变量为序数数据的轮廓,采用非参数模型拟合函数关系,并使用经典的广义似然比(generalized likelihood ratio,GLR)控制图对该函数关系进行监控。
轮廓监控一般分两个阶段进行,即阶段Ⅰ和阶段Ⅱ。阶段Ⅰ是以采集到的历史样本数据为基础,剔除失控(out-of-control,OC)样本点,以确保剩下样本均处于受控(in-control,IC)状态,从而建立稳定的IC模型。阶段Ⅱ是在阶段Ⅰ建立的IC模型的基础上对实时数据进行监控,以及时发现过程异常[1]。阶段Ⅱ控制图的构建往往是假设IC模型已知或者可以被完全精确估计[7-8]。然而,在实际中,模型通常是未知的,需要通过阶段Ⅰ的分析,剔除异常点和变点以确保样本处于IC状态,然后进行模型估计。因为模型估计值具有波动性,所以在监控过程中使用估计值代替已知模型可能会影响阶段Ⅱ控制图的性能。在根据阶段Ⅰ的IC轮廓数据集估计模型时,MAHMOUD[9]评估了监控简单线性轮廓的方案的性能。YAZDI等[10]比较参数估计对监控多元简单线性轮廓的3种阶段Ⅱ方法性能的影响。更多详细内容见文献[11-17]。本文的主要目的是探讨在IC模型未知且被估计量取代的情况下,模型估计对阶段Ⅱ序数轮廓控制图性能的影响。
首先,样本量在模型估计中起较大的作用, JONES等[18]讨论了样本量大小对控制图性能的影响,认为要获得与模型已知时类似的结果,需要较大的样本量。其次,可以选用不同的估计方法,主要分为两大类:参数方法[6]和非参数方法[19]。本文主要使用两种非参数方法即局部线性核估计(local linear kernel estimation,LLKE)和样条法(spline),以及参数方法Newton Raphson。最后,在不同的估计方法中,涉及到相应参数的设置问题(例如LLKE中参数c的取值对估计曲线的平滑度有很大影响)。针对不同的参数设置,本文将通过仿真以及案例进一步探讨样本量大小、估计方法对序数轮廓控制图的IC和OC性能的影响,直观地展现出选择合适的样本量和模型估计方法的重要性。
1 序数轮廓的监控方法
1.1 序数轮廓的回归模型
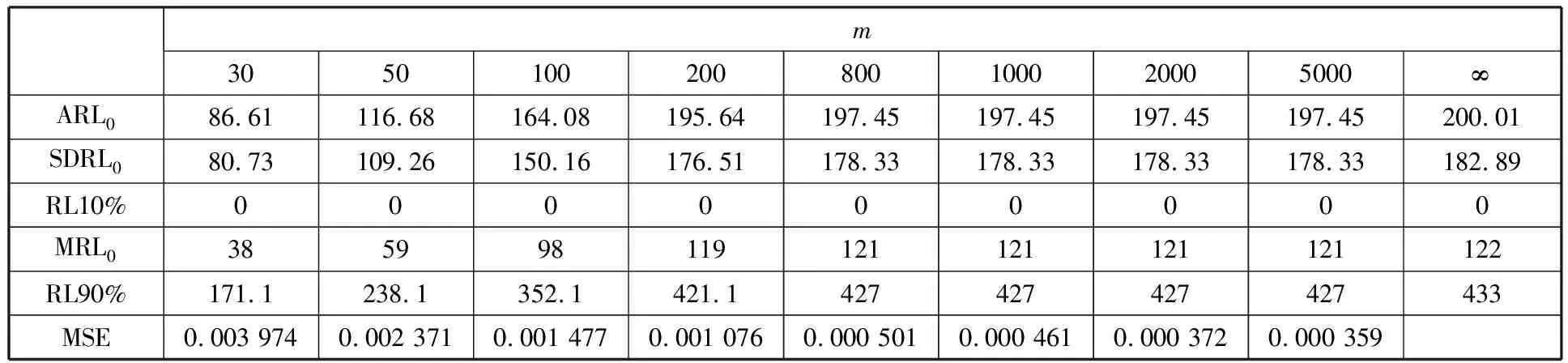
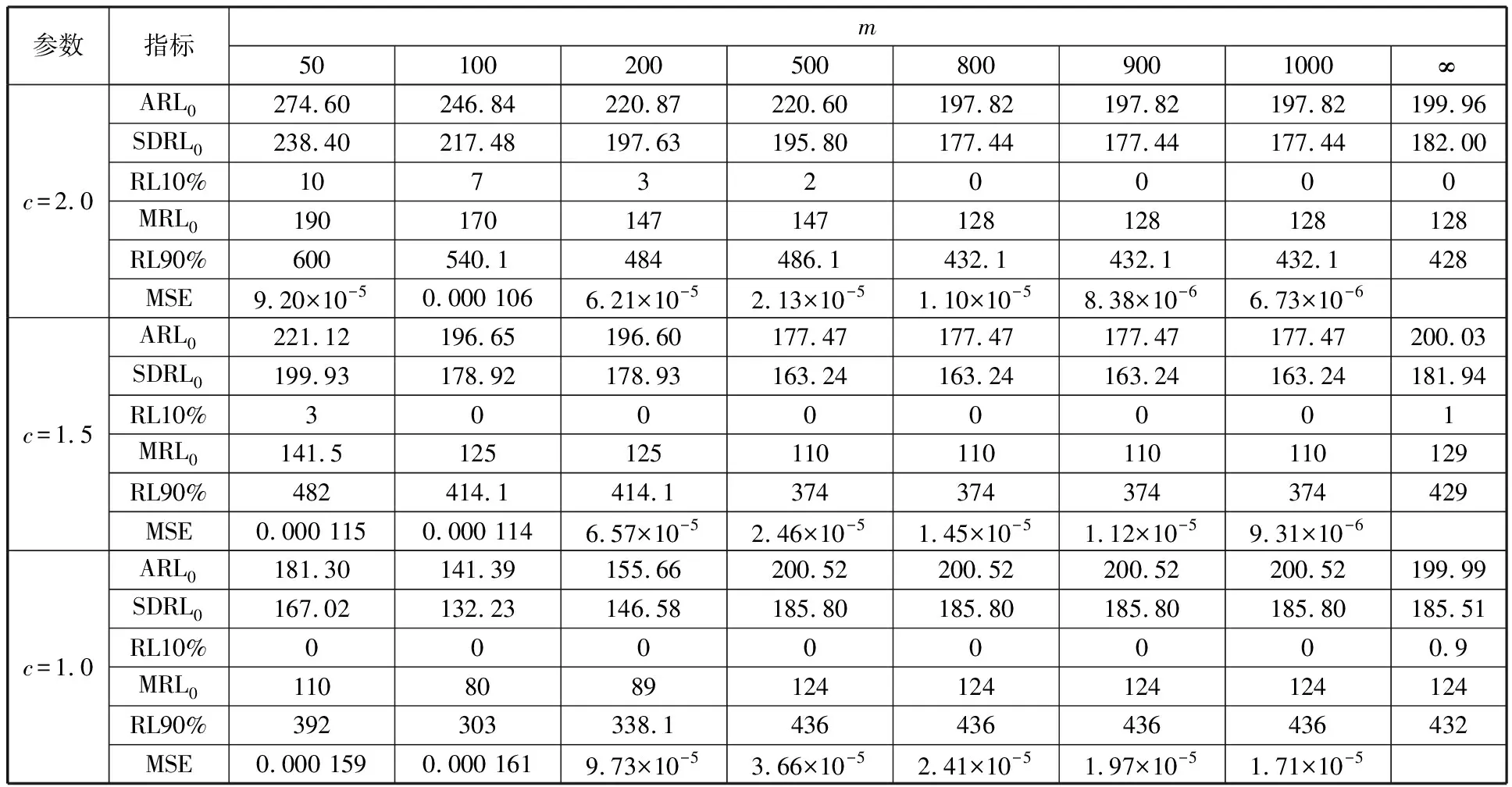
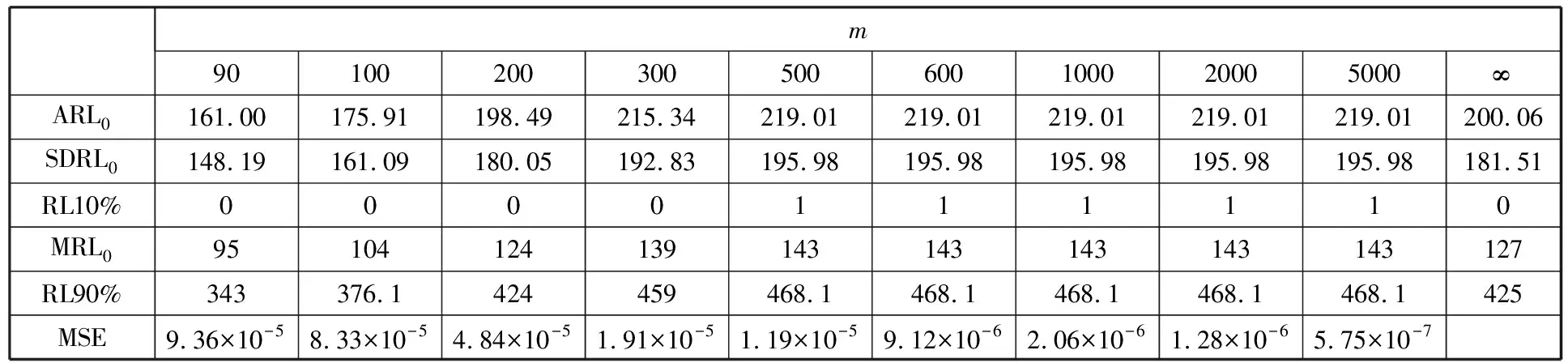
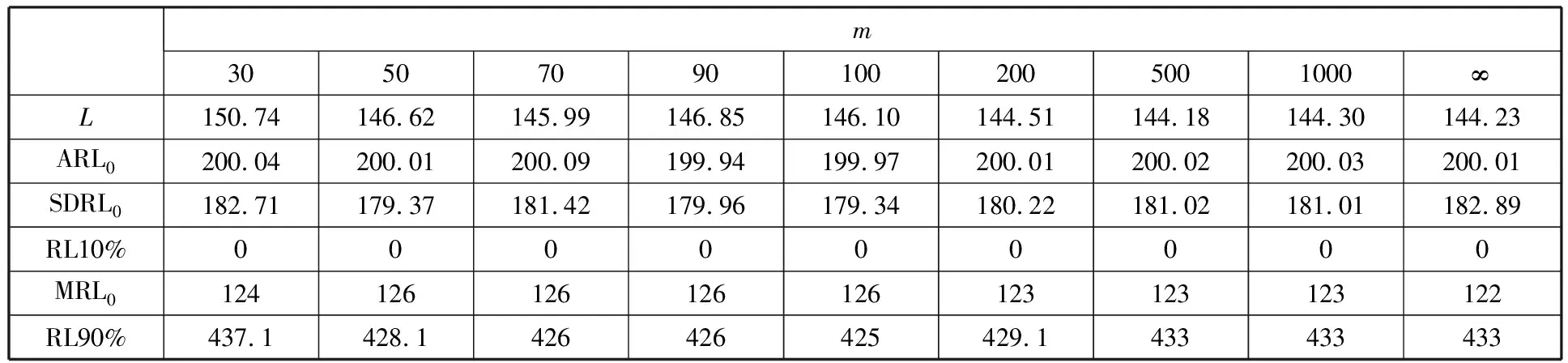
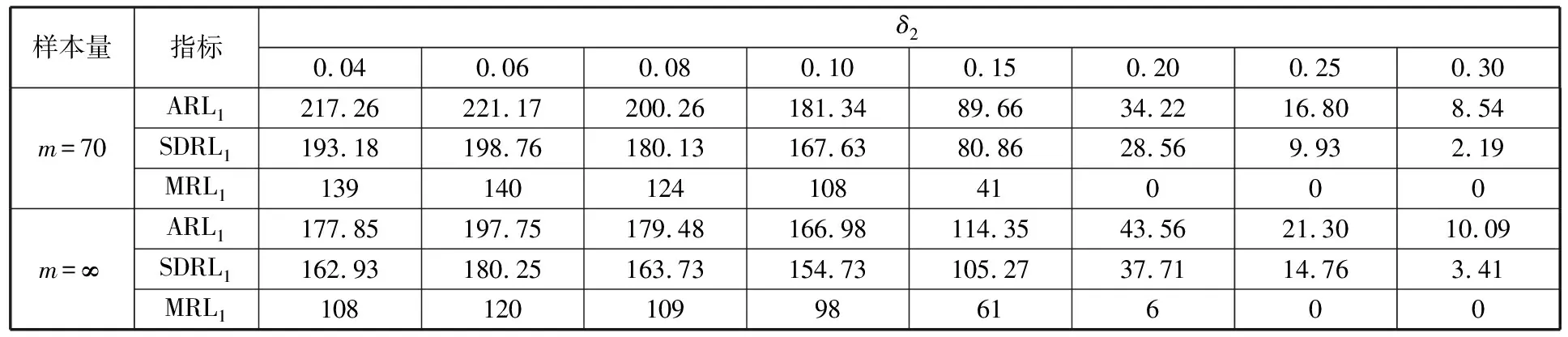
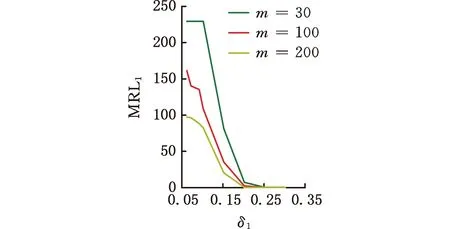
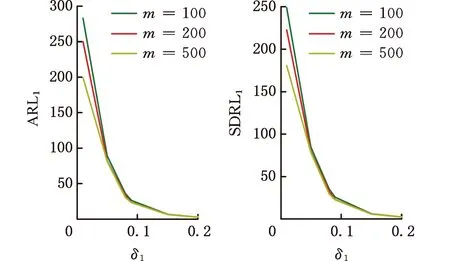
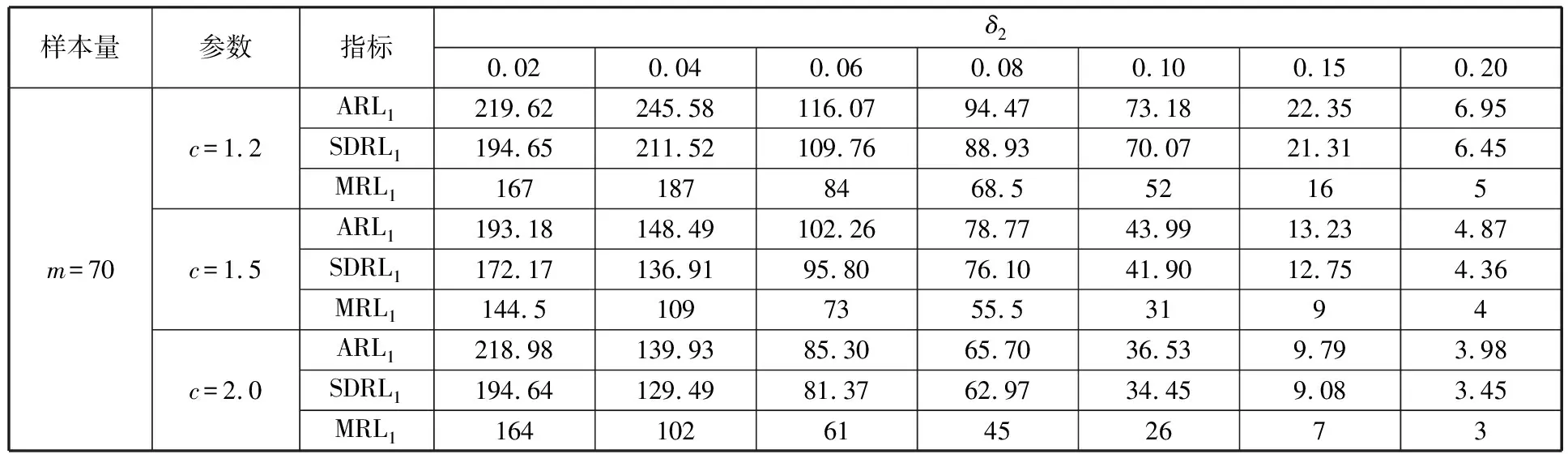
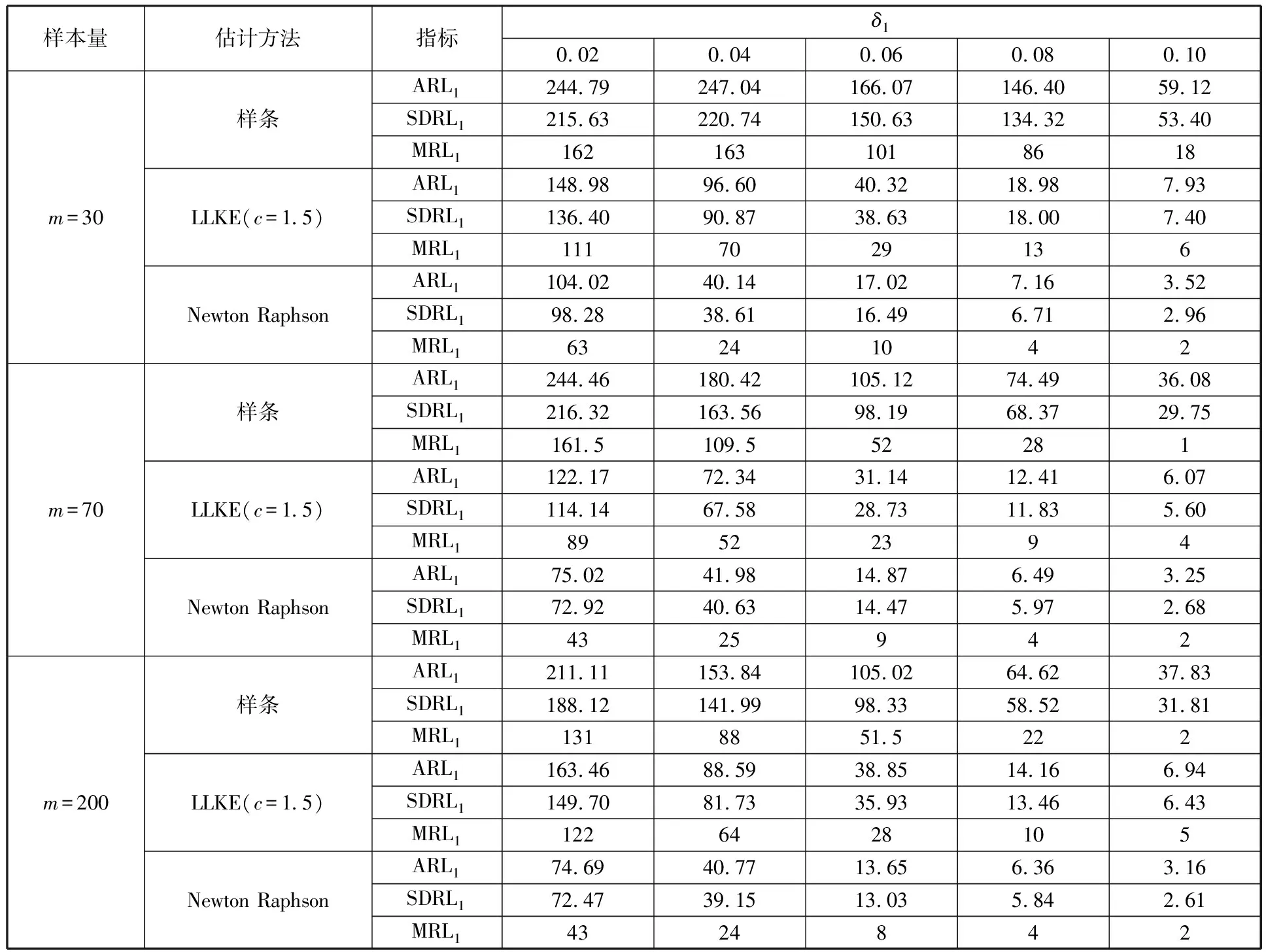
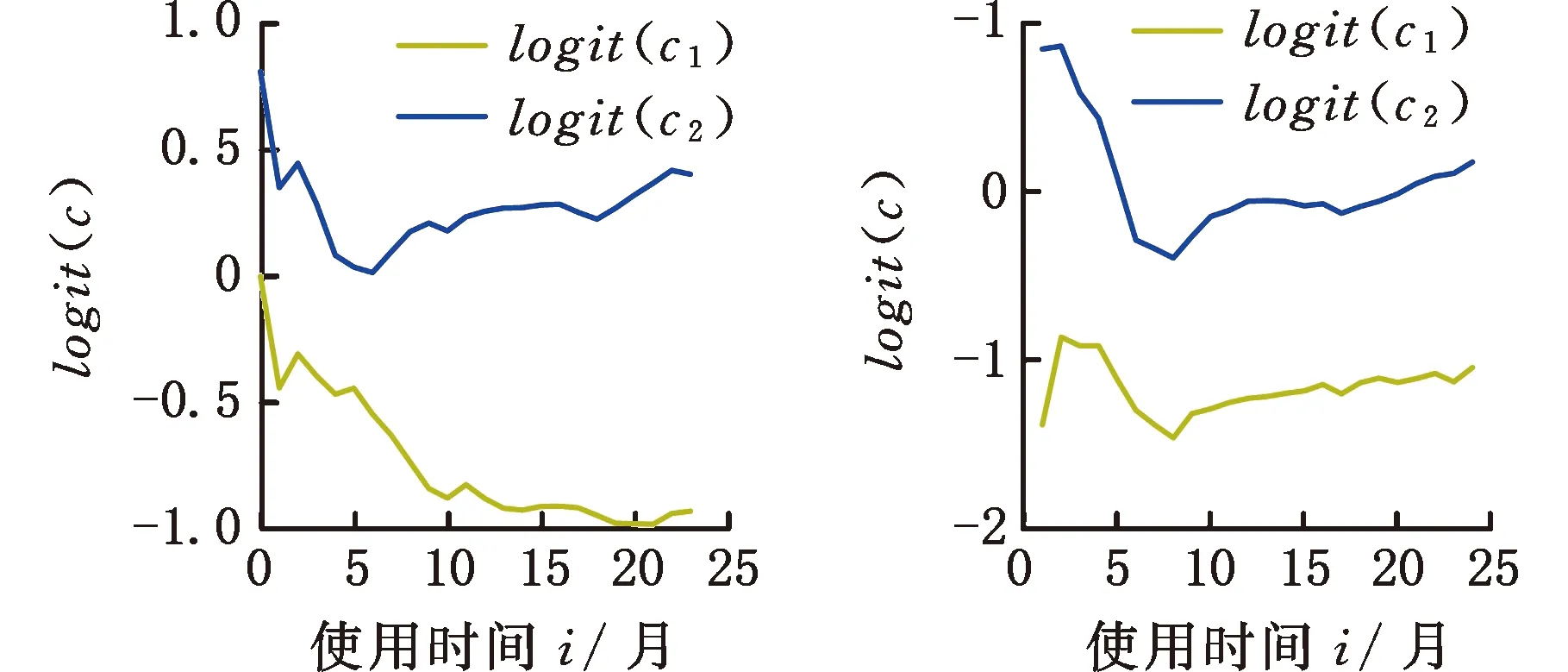
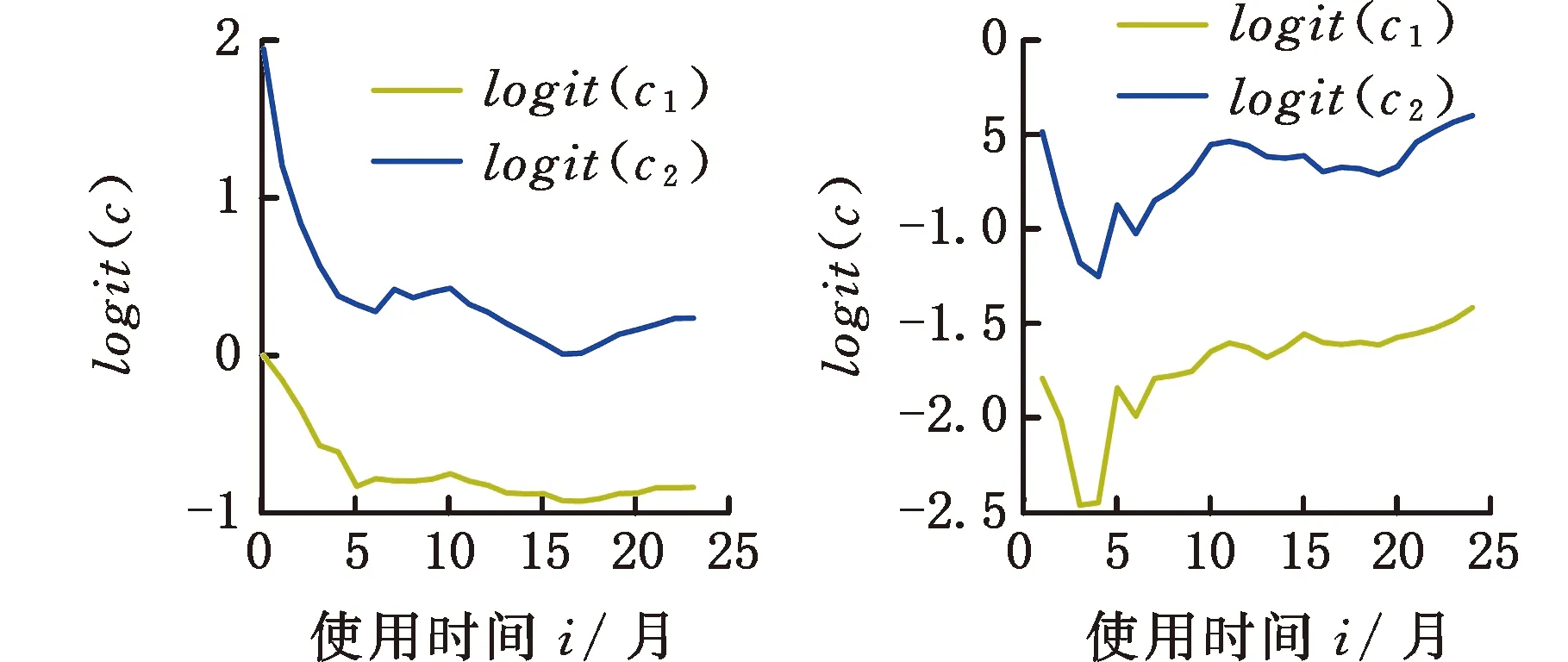
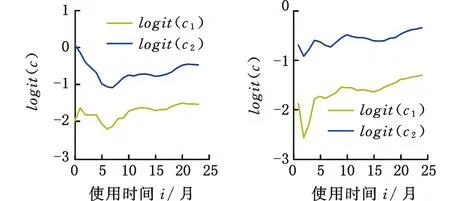
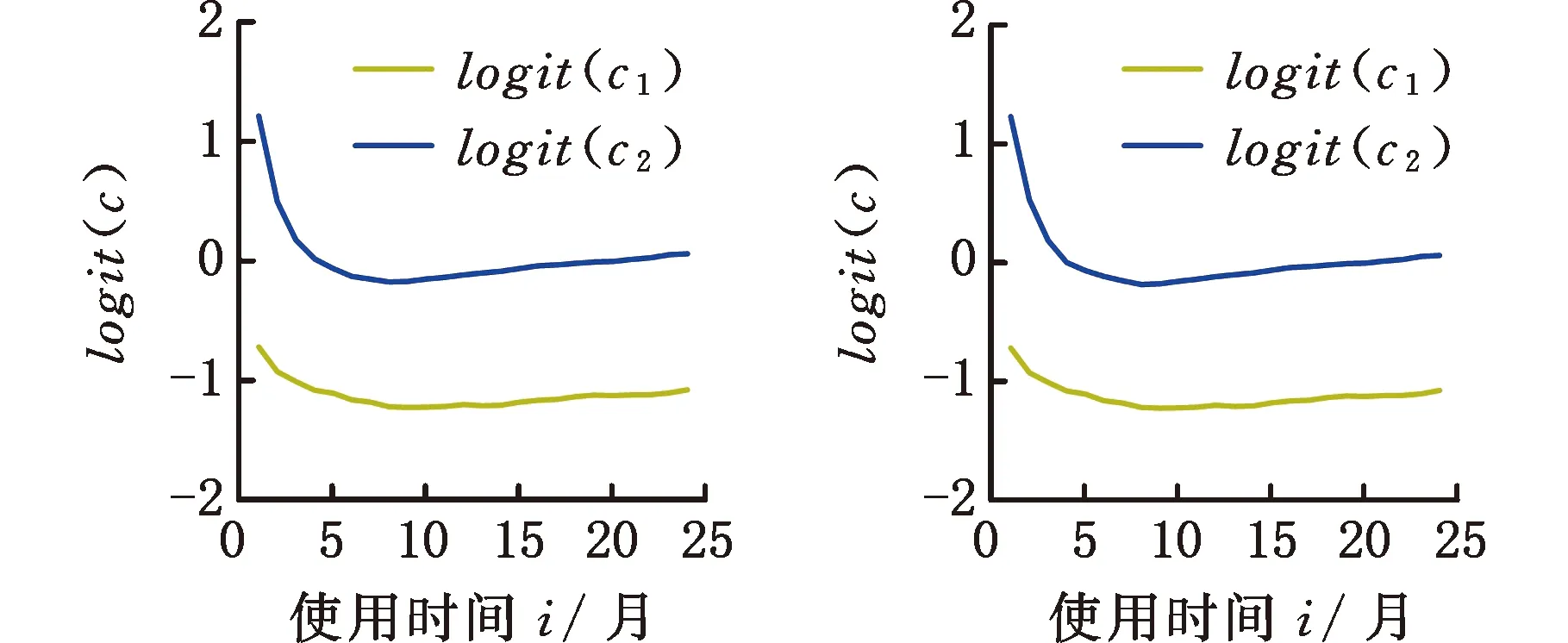
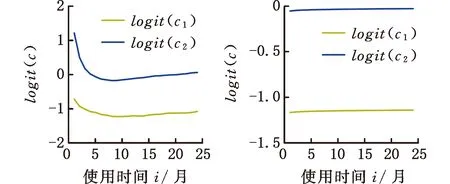
为了简化表示,本文考虑的模型中仅有1个协变量。假设随着时间的推移,收集到第j(j≥1)个轮廓。yji是第j个轮廓中的第i个响应观测值,xi是相应的解释变量(i=1,2,…,Nj),其中Nj是第j个轮廓中的设计点数。假设yji是具有K个属性级别的有序响应变量,且yji服从参数为nji和pji的多项式分布,其中nji=yji1+yji2+…+yjiK,pji=(pji1,pji2,…,pjiK)T。对于不同的j和i,nji取相同的值n,yjik表示第j个轮廓中处在k级的第i个响应变量,pjik表示yji处在k级的概率。令cjik为k级的累积概率(k=1,2,…,K)。因此cjik=Pr(yji 在对序数响应变量和解释变量之间的关系进行建模时,MCCULLAGH[20]提出的比例优势比模型应用较多,IZADBAKHSH等[21]将比例优势比模型作为拟合序数响应变量与解释变量之间函数关系的基础,DING等[6]使用以下参数比例优势比模型对序数轮廓进行建模: logit(ck)=αk+XTβk=1,2,…,K-1 本文使用以下非参数比例优势比模型拟合序数轮廓的回归模型: logit(cjik)=gk(xjik) (1) j=1,2,…i=1,2,…,Njk=1,2,…,K-1 其中,gk(·)是未知的平滑函数;xjik为第j个轮廓中处于k级的第i个响应变量对应的解释变量。 一般来说,轮廓设计点可以是固定不变的(即固定设计)也可以是随机的(即随机设计)。本文只考虑固定设计,将随机设计的方法留待以后研究。也就是说,对于不同的j,取Nj为相同的值N。对于不同的轮廓,解释变量x=(xji,xj(i+1),…,xjN)T是已知且固定的,其中xji表示第j个轮廓的第i个响应变量对应的解释变量。 序数轮廓的响应变量yji服从多项式分布,根据非参数比例优势比模型(式(1)),可以得到第j个轮廓的对数似然函数(省略常数项): (2) 式(1)的监控问题可以看作是回归函数gk(·)的假设检验问题,原假设和备择假设分别如下: 本文主要通过3种模型估计方法对非参数比例优势比模型(式(1))进行估计,分别是非参数方法LLKE、样条法,以及参数方法Newton Raphson。对于这两类模型估计方法,参数方法将轮廓函数拟合为线性、非线性和其他复杂模型,非参数方法则不对模型做过多的假设和约束。本文关注非参数和参数方法在模型估计中的拟合精度问题。 1.2.1局部线性核估计法 局部平滑法是估计非参数函数的常用方法之一。局部拟合方法包括局部常数拟合方法和局部多项式拟合方法。与前者相比,后者在拟合过程中没有边界效应,拟合结果更好。本文利用局部多项式拟合的一种特殊情况——局部线性拟合来估计未知函数gk。 特别地,在给定的x0的邻域内,函数gk(xjik)通过泰勒展开式展开为线性函数: 据FAN等[22]分析可知,对数似然函数(式(2))的核函数为Kh(xji-x0),其中h为带宽参数。因此局部加权对数似然函数可表示为 (3) βk的估计可通过迭代加权最小二乘法(iterative weighted least squares,IWLS)的迭代过程来获得。YEH等[23]简要说明了使用IWLS法估计轮廓参数的步骤。为了便于表达而不影响理解,以下公式省略了一些下标。增广因变量可定义为 zk=(z1k,z2k,…,zNk)T gk=(gk(x1),gk(x2),…,gk(xN))T Wk=diag(w1k,w2k,…,wNk) yk=(y1k,y2k,…,yNk)T μk=(μk(x1),μk(x2),…,μk(xN))T 此外,根据多项式分布的均值和方差公式以及回归函数gk(xi)的估计,可以得到 wik=npik(1-pik)μk(xi)=npik i=1,2,…,Nk=1,2,…,K-1 基于上述条件,可以通过求解以下IWLS方程来获得βk的估计值: Kh(xN-x0)) 使用局部拟合方法的一个重要问题就是确定局部邻域,该邻域主要是由核函数Kh(·)和带宽参数h决定的。本文选取Epanechnikov核函数: 其中,I(·)是指示函数。对于带宽h的选择,建议使用以下经验带宽公式[24]: (4) 1.2.2样条法 样条法不再将样本数据集当作一个整体,而是将它划分成一个个连续区间,划分的点称为节点(knot),并用单独的模型(线性函数或低阶多项式函数)来拟合。 样条估计包括光滑样条估计、多项式样条估计、惩罚样条估计和局部自适应回归样条估计等方法。考虑到本文轮廓解释变量中N的选择问题,以及多项式样条对节点的个数以及位置较敏感,本文选择多项式样条对回归函数gk进行估计。通常情况下,当多项式的阶数达到3时样条法就可获得较高的估计精度,因此针对一个轮廓下的gk,本文使用三次多项式进行拟合。 其中,θs为系数;s为函数f(x)的项数。令gk(x)=fk(x)+ε(ε为误差项),则回归函数gk(x)的估计问题转化为gk(x)-fk(x)=ε的最小化问题: 令 以上为使用三次样条估计gk的大致过程,在仿真部分本文使用的是三次样条插值法,可直接调用Python中程序包完成模型估计。 1.2.3NewtonRaphson方法 Newton Raphson方法在统计中广泛应用于求解最大似然估计。对于序数轮廓,可强制使用广义线性模型拟合,然后采用Newton Raphson算法进行参数估计[6]。本文目标函数为对数似然函数(式(2))极大化,可转化为求解函数l(·)的一阶导函数l′(·)=0的问题。具体迭代步骤如下: (1)将目标函数l(·)在给定的x0的邻域内,通过泰勒展开式展开到二阶形式: (5) 当且仅当Δx=xji-x0无线趋近于0时,式(5)得以成立,此时式(5)等价于: (2)计算迭代公式: 其中,v为迭代次数,v≥0。 (3)结合对数似然函数(式(2)),令 k=1,2,…,K-1 其中,Ak为关于gk的函数,则式(2)可以转化为有关gk的K元函数f(·): (4)对函数f(·)求偏导,计算迭代公式: Xv+1=Xv-[Hf(Xv)]-1f(Xv) 其中,H为Hessian矩阵。 (5)将Xv+1代入步骤(3)中的K元函数f(·),重复步骤(4)、步骤(5),直至|Xv+1-Xv|<ζ(ζ为搜索精度),终止计算。 GLR控制图的应用范围较广,例如监控正态分布的均值或方差等。由于GLR统计量的良好性质,本文基于GLR统计量构建控制图对非参数比例优势比模型(式(1))进行监控。3种估计方法下GLR统计量定义如下。 LLKE方法下的统计量: 样条和Newton Raphson方法下的统计量为 控制限L(1)和L(2)可用二分法搜索,具体迭代步骤如下: (1)在第i次迭代计算中,在区间[L(i),U(i)]中搜索L*。当i=1时,令L(1)=0和U(1)=U,其中U是满足以下条件的上限,即L*=U时控制图的平均运行链长(average run length,ARL)值大于预先指定的受控状态下的ARL值ARL0。 (2)将搜索区间折半,即L*=l(i)=(L(i)+U(i))/2,然后计算对应控制限L*下的运行链长(run length,RL)。 常用的阶段Ⅱ控制图性能评价指标是ARL值。控制图在IC状态下的性能主要是通过ARL值ARL0进行评估,对于OC性能,ARL值的计算存在零态和稳态两种假设。本文使用稳态OC下的ARL值ARL1作为一个指标来比较不同估计方法下的控制图的OC性能。理想情况下,在ARL0相等的情况下,对于给定的偏移,具有较小ARL1的控制图通常被认为具有更好的性能。除此之外,用运行链长的标准差(standard deviation of run length,SDRL)和运行链长分布的百分位数来更全面地评估控制图的性能。在分析控制图的IC性能时,本文主要通过ARL0、SDRL0、运行链长的10%分位数RL10%、运行链长的中位数(median run length)MRL0和90%分位数RL90%来评价控制图的性能。通过均方误差(mean square error,MSE)来评价不同估计方法的精确度。OC状态下的评价指标包括ARL1、SDRL1以及MRL1指标。 采用二分搜索法,通过5000次重复仿真,逼近相应控制图的控制限。为了便于说明,变化点设置为τ=25。为了评估每个控制图的稳态ARL值ARL1,在第(τ+1)个观测值之前发生警报的任何仿真序列将被舍弃。对于多项式分布中的参数,假设n=50。另外,带宽h由式(4)确定,常数c取3个不同的值,分别为1、1.5和2。不失一般性,假设每个序数轮廓样本中有N=50个等距设计点,有 假设序数响应变量具有3个水平,即K=3,非参数比例优势比模型(式(1))可以写为 logit(cji1)=g1(xji)logit(cji2)=g2(xji) i=1,2,…,Nj=1,2,… 本文主要考虑了广义线性模型(generalized linear model,GLM)为受控模型的情况。 GLM受控模型为 logit(cjik)=αk+βxi i=1,2,…,Nj=1,2,…k=1,2 如DING等[6]所述,响应变量y的序数水平主要由截距决定,系数β反映x对y的影响。本文仍采用与DING等[6]相同的参数设置。考虑到响应变量之间的序数信息,系数选择为(α1,α2)=(-1,0.5),β=0.2。 表1、表2、表3所示为在不同样本量m下,分别使用样条、LLKE和Newton Raphson估计方法时,GLR控制图的ARL0、SDRL0、RL10%、MRL0和RL90%值。注意,表1、表2和表3的最后一列给出的是m=∞时控制图的IC性能,即GLR控制图在回归模型已知条件下的性能。在每张表的最后一行,给出了不同样本量下估计的均方误差MSE。 表1 样条方法下GLR控制图的IC性能 一方面,从表1中可以看到随着样本量m的增大,GLR控制图的各项评价指标越来越接近模型已知条件下的各指标值。在样本量m≤800时,ARL0、SDRL0、MRL0和RL90%值呈现出递增的趋势,即样条方法下产生的虚报警次数在减少。当样本量增至800后,再继续增大样本量,GLR控制图性能的各项指标不再发生变化。换言之,在样本量m=800时,使用样条方法就可以达到较好的估计效果,即此时样条估计对控制图性能的影响较小。 表2 LLKE方法下GLR控制图的IC性能 表3 Newton Raphson 方法下GLR控制图的IC性能 另一方面,根据MSE不难发现,随着样本量m的增大,MSE呈现出递减的趋势,即估计精度提高。最后,从表1中可以发现,样本量m从30增大至800时,ARL0、SDRL0等指标的数值跨度较大,这也说明使用样条方法估计回归模型时,样本量对GLR控制图的性能影响显著。 表2总结了LLKE方法下GLR控制图在不同样本量及参数c下的IC性能。在c=2和1.5时,GLR控制图的ARL0、SDRL0、RL10%、MRL0和RL90%指标均随着样本量m的增大而递减。当c=2时,在样本量m=800处GLR控制图的IC性能与m=∞时的性能最接近,此时使用LLKE估计非参数比例优势比模型(式(1))对GLR控制图的IC性能影响最小。当m>800时,LLKE对控制图IC性能的影响不再随着样本量的增大而变化。当c=1.5时,在样本量m=100处GLR控制图的IC性能受LLKE估计的影响最小。在c=1的情况下,当样本量达到500时,LLKE估计方法下GLR控制图的IC性能与模型已知情况下的差距最小,继续增大样本量,控制图IC性能指标不再发生变化,即m=500时,使用LLKE可获得较好的估计效果。 观察不同参数c下各样本量对应的MSE指标,可以发现MSE指标均随着样本量的增大而递减,即样本量越大,取得的估计效果越好。但是,当样本量较大时,MSE数值变化较小,因此,在使用LLKE方法估计回归模型时,使用小样本就可达到较高的估计精度。对比不同参数c下的GLR控制图的IC指标不难发现,在m≤200时,随着c的减小,各指标呈现出递减的趋势。当m≥500时,各参数c下GLR控制图的IC性能几乎不再受样本量大小的影响,小样本量时控制图已可以获得较好的IC性能。 观察表3,首先,随着样本量m的增大,在Newton Raphson 方法下GLR控制图的各项IC指标呈递增的趋势。当样本量m=200时,控制图的性能指标与模型已知时的性能差距较小。后续随着样本量继续增大,ARL0、SDRL0、MRL0和RL90%等指标逐渐远离m=∞时的数值,且当m≥500时,GLR控制图的各性能指标不再发生变化。再者,对比不同样本量下的MSE指标可以发现,随着样本量的增大,MSE的递减幅度较小,这表明在样本量m=200后再继续增大样本数量对Newton Raphson方法的估计效果影响不大。因此,在使用Newton Raphson方法估计GLM时,小样本量也可达到较好的估计效果。 综合表1、表2和表3,对比3种模型估计方法所需的最小最优样本量,在IC模型是GLM时,与非参数方法相比,使用参数方法Newton Raphson可以达到较高的估计精度,对阶段Ⅱ的GLR控制图的IC性能影响较小。 由以上分析可知,模型估计会影响GLR控制图的IC性能,而适当增大样本量会降低该影响,但由于成本或其他限制,收集大量样本比较困难,在这种情况下,调整控制限也可以补偿模型估计带来的影响。本文通过模拟实验,调整GLR控制图在不同估计方法下的控制限,使其具有预定的ARL0约等于200。样条方法下对应的GLR控制图的调整后的控制限见表4。根据表4可知,在样本量一定的情况下,控制图各性能指标相对调整控制限之前更加接近m=∞时的性能指标。当m=30时,仅看MRL0指标,表1中调整控制限之前MRL0为38,表4中MRL0为124,显然后者更接近m=∞时的MRL0值122。在LLKE和Newton Raphson方法下,可以得到相同的结论。 表4 调整控制限后样条方法下GLR控制图的IC性能 对于OC模型,本文仅选取了一种有代表性且易于理解的OC模型进行仿真研究:只改变模型系数,响应变量与解释变量之间的函数关系结构不变。失控模型如下: logit(cjik)=(αk+δ1)+(β+δ2)xi i=1,2,…,Nj=1,2,…k=1,2 为了评估失控状态下使用不同的估计方法对阶段Ⅱ的GLR控制图OC性能的影响,本文主要考虑了3个样本量范围。为了公平比较控制图的OC性能,应确保ARL0相同,因此采用调整后的控制限。首先在样本量一定的情况下,评价样条和Newton Raphson方法对GLR控制图OC性能的影响。接着,当样本量发生变化时,分析控制图性能指标的变化情况。最后,在不同样本量下,比较样条、LLKE和Newton Raphson方法下控制图的OC性能指标,找到在IC模型为GLM时,参数和非参数模型估计方法适用的样本量范围。 表5和表6分别总结了在使用样条和Newton Raphson估计方法的情况下,当参数β发生偏移时,GLR控制图在样本量m=70和∞下的ARL1、SDRL1和MRL1的数值。从表5和表6中可以发现,GLR控制图的OC性能受到模型估计的影响。当使用样条估计模型时,如果参数发生的偏移较小,则该估计方法会带来较大的负面影响;当偏移较大时,则估计对控制图性能的影响较小。使用Newton Raphson估计回归模型时,无论参数β发生的偏移大小,该方法均会对GLR控制图的OC性能产生明显的负面影响。 表5 样条估计方法对GLR控制图OC性能的影响(β偏移) 表6 Newton Raphson估计方法对GLR控制图OC性能的影响(β发生偏移) 图1和图2分别给出了样条和Newton Raphson方法在3种不同的样本量下,当参数α发生偏移时,GLR控制图的OC性能指标。从图1中可以看到,在同一样本量m下,随着偏移的增大,ARL1、SDRL1和MRL1均呈现出递减的趋势,即参数发生的偏移较大时,GLR控制图能够快速检测出异常并发出警报。另外,在偏移量相同的情况下,m=30时的控制图的各项OC指标远远超过m=200时的指标,即GLR控制图的检出力度随着样本量的增大而增强。因此,适当增大样本量可以减小模型估计对控制图OC性能的影响。由图2可以得出类似的结论,但与样条方法不同的是,使用Newton Raphson估计回归模型时,随着样本量m的增大,同一偏移下的各OC指标的差距较小。因此,使用Newton Raphson方法估计模型时增大样本量m,对控制图检出力的影响并不显著。 (c)MRL1的对比图1 样条方法下样本量对GLR控制图OC性能的影响(α偏移)Fig.1 The effects of sample sizes on OC performanceof GLR control chart under spline method(α shifts) (a)ARL1的对比 (b)SDRL1的对比 (c)MRL1的对比图2 Newton Raphson方法下样本量对GLR控制图OC性能的影响(α偏移)Fig.2 The effects of sample sizes on OC performanceof GLR control chart under Newton Raphsonmethod(α shifts) 通过以上对不同样本量下使用样条和Newton Raphson方法时的GLR控制图的OC性能分析可知,样本量对阶段Ⅱ控制图性能的影响因估计方法的不同而有所不同,所以在实际应用时,应根据样本量的大小谨慎选择模型估计方法。在LLKE方法下,式(4)中的参数c对估计曲线的平滑度有较大影响,进而会影响最终的模型估计结果。因此,对于LLKE方法,本文重点关注参数c对GLR控制图OC性能的影响。表7所示为样本量固定为70的情况下,使用LLKE方法估计模型时,GLR控制图的OC性能指标。根据表7可得,在同一参数c下,当参数β发生偏移时,随着偏移量的增大,GLR控制图的OC性能指标呈递减的趋势;当偏移量固定时,随着参数c的增大,ARL1、SDRL1和MRL1大致呈递减的趋势,GLR控制图的OC性能随着c的递增而增强。 表7 LLKE估计方法对GLR控制图OC性能的影响(β偏移) 对比分析不同的样本量下采用这3种估计方法的控制图OC性能指标,得出3种模型估计方法分别适用的样本量范围。本文选取了样本量分别为30,70,200的3种情况进行简单解释。当参数α偏移时,GLR控制图的OC性能指标数据见表8。 表8 不同样本量下样条、LLKE(c=1.5)和Newton Raphson三种估计方法对GLR控制图OC性能的影响(α偏移) 由表8可以发现,首先,对于同一种估计方法,随着样本量的增大,GLR控制图的ARL1、SDRL1和MRL1指标均呈现出递减的趋势,即在大样本量情况下控制图的OC性能更优,该结论与图1和图2一致。其次,当样本量固定在30时,比较3种估计方法下GLR控制图的OC性能可以发现,Newton Raphson方法下控制图的OC性能最优,无论偏移大小,控制图均能够及时发现变点,LLKE(c=1.5)次之,而样条方法下控制图的OC性能最差。在m=70和200时可以得到同样的结论。因此,当IC模型为GLM且样本量m≤200时,使用参数方法Newton Raphson可以获得较好的GLR控制图OC性能。 在仿真过程中,本文假设IC模型为GLM,该假设与参数方法Newton Raphson的假设一致,因此使用Newton Raphson估计模型时,GLR控制图的性能较好。但对于复杂的函数关系,无法使用GLM拟合模型。通过以上仿真可以发现,在IC模型为GLM时,LLKE方法下的控制图性能仅次于Newton Raphson,因此在模型为非GLM或未知时,推荐使用LLKE。 为了进一步检验LLKE、样条和Newton Rapson方法的估计效果,本文将3种方法应用于一个汽车制造商的保修索赔的数据集。汽车是最常见的带有保修合同的产品之一,在保修期内,制造商有义务免费维修或更换保修合同范围内的瑕疵产品。汽车投入使用后,将每天(每周或每月)发生的保修索赔次数记录在保修数据集中,通过对保修索赔数据建模分析,可尽早发现质量或现场可靠性问题[25]。通常假定同一天生产的产品具有相同的可靠性[26]。 在本文所使用的保修索赔数据集中,每周生产的汽车总数量中的累计保修索赔数量是按照汽车使用月份记录的。为了排除其他因素的影响,本文只考虑在特定车型和型号下汽车发动机的保修索赔情况。因为发动机的保修期通常不少于两年,所以选择对汽车销售后24个月的索赔数据进行分析。数据集中提供了故障类型(从工程角度)和每种故障类型下的保修索赔数量。通过整理数据发现,所有故障类型按照发生频次可归纳为轻微、中等、严重3种故障类型。案例中的质量特征是一个轮廓,其中响应变量是不同故障类型的累计保修索赔数量,解释变量是使用月份。数据集中共有52个保修索赔的轮廓,图3显示了6个具有代表性的轮廓(第19个轮廓到第24个轮廓)的logit(c)图。由图3可以看出,图3c与图3d之间存在明显的差异,即从第22个轮廓开始,函数模型开始发生变化。因此,在案例研究中前21个轮廓作为IC参考数据。 (a)第19个轮廓 (b)第20个轮廓 (c)第21个轮廓 (d)第22个轮廓 (e)第23个轮廓 (f)第24个轮廓图3 IC和OC状态下的轮廓的logit(c)曲线Fig.3 The logit(c) curve of the profile in IC andOC states 采用非参数比例优势比模型(式(1))来表示响应变量y与解释变量X之间的函数关系。 综上,当IC模型是GLM时,本文推荐使用Newton Raphson,该方法所需估计样本量较少,且可以获得较好的估计效果。当IC模型形式不明确时,本文推荐使用非参数方法LLKE和样条。 (a)基准 (b)LLKE (c)样条(d)Newton Raphson图4 使用LLKE、样条和Newton Raphson方法的模型估计结果与基准对比Fig.4 Comparisons of Benchmark with the estimationresults using LLKE, spline and Newton Raphson method 本文评估了使用样条、LLKE和Newton Raphson 3种估计方法对序数轮廓控制图的IC和OC性能的影响。首先,本文通过ARL0、SDRL0、RL10%、MRL0和RL90%等指标评价了3种模型估计方法对GLR控制图IC性能的影响。通过对比发现,一方面增加样本量可以减少模型估计对控制图性能的影响,但是当样本量增加到一定程度之后,继续增加样本量所到来的效果并不理想。另一方面在IC模型为广义线性模型(GLM)时,3种估计方法中,Newton Raphson方法对样本量大小的要求不高。其次,当IC模型由GLM变为另一种线性模型时,本文评估了GLR控制图在3种估计方法下的OC性能。通过ARL1、SDRL1和MRL1指标可以发现,在样本量固定的情况下,样条、LLKE和Newton Raphson均会影响控制图OC性能,但参数方法Newton Raphson可以获得较好的估计效果,即在OC模型仍为GLM时Newton Raphson对GLR控制图的OC性能影响较小。再者,本文对比了不同样本量下使用3种估计方法时控制图的OC指标,发现当IC模型为GLM时,参数方法较非参数方法可以达到较高的估计精度,且对控制图性能影响较小。最后,本文通过一个实际案例进一步说明了当IC模型不明确时,非参数方法可以获得较高的估计结果精确度。 本文存在以下两点不足。第一,本文主要针对IC模型为GLM的情形研究了模型估计对序数轮廓控制图性能的影响,对其他更复杂的IC模型没有做细致的说明。在实际应用场景中,IC模型的具体表现形式不得而知,因此仿真情景中,可适当增加较复杂的模型以进行更完善的研究。第二,LLKE中的参数c对估计精度有较大的影响[19],关于模型估计对序数轮廓控制图性能的影响以及LLKE方法下的参数c的影响可做进一步研究。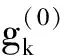
1.2 模型估计方法

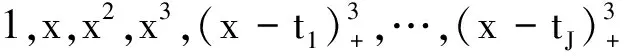

1.3 监控序数轮廓的控制图
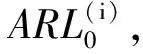
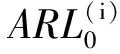
2 控制图IC性能分析
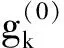
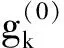
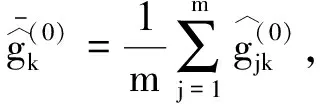
3 控制图OC性能分析


4 案例研究
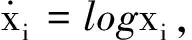
5 结论及展望

