关于对换改变排列反序数的奇偶性的一种推理方法
常加强
(咸阳师范学院计算机学院,咸阳 712000)
关于对换改变排列反序数的奇偶性的一种推理方法
常加强
(咸阳师范学院计算机学院,咸阳712000)
对《高等代数》中行列式排列理论的补充,从另一个角度证明和推理对换改变排列反序数的奇偶性,得出原排列反序数与对换后新排列反序数之间的关系及公式,使对换改变排列反序数的奇偶性更加清晰。
排列;对换;反序数;奇偶性
0 引言
对于《对换改变排列反序数的奇偶性》这一问题的研究,其理论体系几乎完闭和严密,所以目前对于该问题的研究相对较少。张禾瑞[1]等从另一方面对该问题做了理论上的证明与推理,得出原排列反序数与对换后新排列反序数之间的关系及公式,该理论简单、易懂,初学者能够更加直观地看到对换确实改变了排列反序数的奇偶性。本文另辟蹊径,再次证明了《对换改变排列反序数的奇偶性》这一问题。
1 奇偶性的推理
已有的资料显示[2-5],对于排列问题每一个对换都可以改变排列的奇偶性。即,一个排列m1,m2,…,mn经过(mk1,mk2)对换,则改变此排列反序数的奇偶性,如果知道原排列的反序数,如何利用简便算法,求得经过对换后得到新排列的反序数呢?或者说能不能给出原排列的反序数与新排列的反序数之间一个关系式?使大家更加明白,每一个对换都改变排列的奇偶性。
证明:
设式(1)为原排列,式(2)为经对换后的新排列,式(3)新排列的反序数
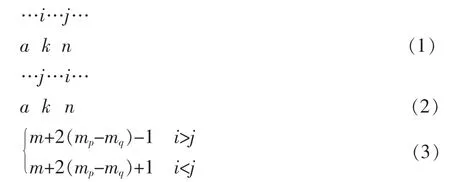
(1)当i>j时
在k个数码中有mq个数码大于,则有k-mq个数码小于j,由于a个数码,n个数码及k个数码的位置次序没有变,则由它们构成的部分排列的反序数没有变。对排列

来说,j的反序数mj=mq+1。经过对换(i,j)得到新的排列为:

则,j的反序数为mj=0,但j和其他数码构成的反序数为k-mq,那么,从数码j的角度来看,经过对换(i,j),排列(4)变为排列(5),其反序数增加了
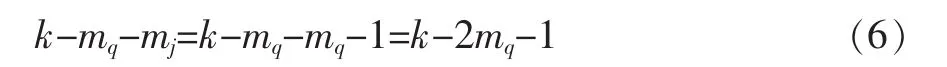
设k个数码中小于i的数码为m1个,对于排列(4)来讲,i和其他数码构成反序数为m1,(j除外,因为i与j构成反序已经计算过了),则在排列(5)中,i的反序数为m2=k-m1,从i的角度来讲,反序数增加了

则排列(4)经过对换(i,j)得到新的排列(5),其反序数增加了

对于排列(1)来讲,由于i和j的对换不影响i和j分别和a+n个数码构成排列的反序数,显然就有排列(1)经过(i,j)对换得到新排列(2),其反序数增加为:

(2)当i<j时,同理可证。
[1]张禾瑞,郝鈵新.高等代数[M].北京:高教出版社.
[2]王萼芳.高等代数[M].北京:清华大学出版社.
[3]郭龙先,张毅敏,何建琼.高等代数[M].北京:科学出版社.
[4]高孝忠.高等代数[M].北京:清华大学出版社.
[5]黄益生.高等代数[M].北京:清华大学出版社.
[6]秦松喜.高等代数新编[M].厦门:厦门大学出版社.
排列(1)经过(i,j)对换得到新排列(2),其反序数增加为m+2(mp-mq)+1。
故此定理证毕。
举例:将排列4513627经过对换(1,2)得到新的排列4523617
排列(1)的反序数m1=2+4+2+0+0+0+0=8
排列(2)的反序数m2=5+2+2+0+0+0+0=9
现用上面证明的公式:
由于1<2其中mp=mq=2
则有m1+2(mp-mq)+1=9,m2=9
即两个计算的结果相同。
2 结语
本文从另一个角度证明和推理了对换改变排列反序数的奇偶性,得出原排列反序数与对换后新排列反序数之间的关系及公式,使对换改变排列反序数的奇偶性更加清晰。
A Novel Reasoning Method about the Parity of Ordinal Numbers
CHANG Jia-qiang
(School of Computer Science,XianYang Normal University,Xianyang 712000)
This is a supplement of determinant permutations.It proves the parity of arrangement and inverse order via swapping.Thus,the relationship is deduced between inverse order of original arrangement and swapped arrangement,so as the property of swapped arrangement is easy to understand.
Arrangement;Swapping;Inverse Order;Parity
1007-1423(2016)26-0036-02DOI:10.3969/j.issn.1007-1423.2016.26.009
常加强(1963-),男,陕西咸阳人,本科,讲师,研究方向为信息与计算科学
2016-07-07
2016-09-07
计算机科学与技术专业嵌入式方向“团队式”人才培养模式创新实验区(No.26)

