机械传动系统运动精度优化分配新方法

李 健 冉 琰 张根保 王勇勤

重庆大学机械与运载工程学院，重庆， 400044

0 引言

精度是数控机床等机电产品的主要性能指标之一，通过精度设计可以保证机械产品的精度。精度设计包括精度分析和精度分配，二者互为相反的过程。国内外学者对精度分配技术进行了大量的研究。余治民等[1]利用多体系统理论和坐标变换方法，建立了龙门导轨磨床几何误差的传递模型，并在此基础上对磨床精度进行了优化分配。王海艳等[2]利用统计方法建立了螺旋铣孔专用主轴单元的精度分配模型，并综合考虑权重影响系数和精度储备系数等因素，实现了主轴单元的精度分配。CHENG等[3-4]利用多体系统理论建立了数控机床的体积精度模型，并在此基础上实现了多轴机床几何精度的优化分配。ZHANG等[5]利用多体系统理论建立了数控机床的体积误差模型，给出了机床各部件的误差与体积误差之间的耦合关系，提出一种同时考虑几何误差和热诱导误差的零件几何精度分配方法。吕程等[6]基于多体运动学理论建立了机械系统装配体误差模型，并结合装配体精度要求进行了结合面精度的优化分配。武剑[7]利用齐次坐标变换方法建立了三轴加工中心的误差模型，并在此基础上建立了精度优化分配模型，实现了整机-部件-零件的逆向精度分配。徐彦伟等[8]提出了一种面向零件加工精度要求的弧齿锥齿轮铣齿机主动精度设计方法，通过建立零件加工精度要求和机床数控轴重复定位精度之间的映射关系，实现了精度的合理分配。

上述方法实现了数控机床等复杂机电产品精度的优化分配，但误差建模和分析均基于静态误差建模方法。数控机床等复杂机械系统的运动误差是通过零部件的相对运动产生的，静态误差建模方法无法反映机械系统精度的形成机理。因此，宋江波等[9]通过研究影响数控机床传动精度的主要因素，建立了机床传动系统精度可靠性的分析模型，并提出了提高传动系统精度可靠性的措施。吴凤和等[10]建立了双摆角铣头传动链的运动误差模型，并提出一种考虑灵敏度与加权分配的运动精度定量分配方法。上述分析方法从传动链误差形成机理出发，实现了运动精度的分析和优化分配，但这些方法需要对整条传动链进行建模，分析过程比较繁琐，在实际应用中存在很大的局限性。

因此，本文结合元动作理论，提出一种机械传动系统运动精度优化分配新方法。首先利用“功能-运动-动作”(function-motion-action, FMA)分解树将机械传动系统进行结构化分解，得到元动作链和基本的元动作；然后，将元动作链的运动精度分配给各个元动作，得到元动作运动精度，最终实现机械传动系统运动精度准确合理的分配。

1 元动作理论介绍

1.1 FMA结构化分解树

笔者所在团队利用元动作理论对复杂机电产品的可靠性、精度等质量特性进行研究[11-14]。通过元动作理论的FMA结构化分解树可对复杂机械系统进行结构化分解，得到各个串联的元动作，如图1所示。整机的性能通过各个元动作以及元动作之间的连接性能来实现，因此，以元动作为基本单元对复杂机电产品的质量特性进行研究，实现机械系统的模块化分析，降低分析的难度和复杂性。

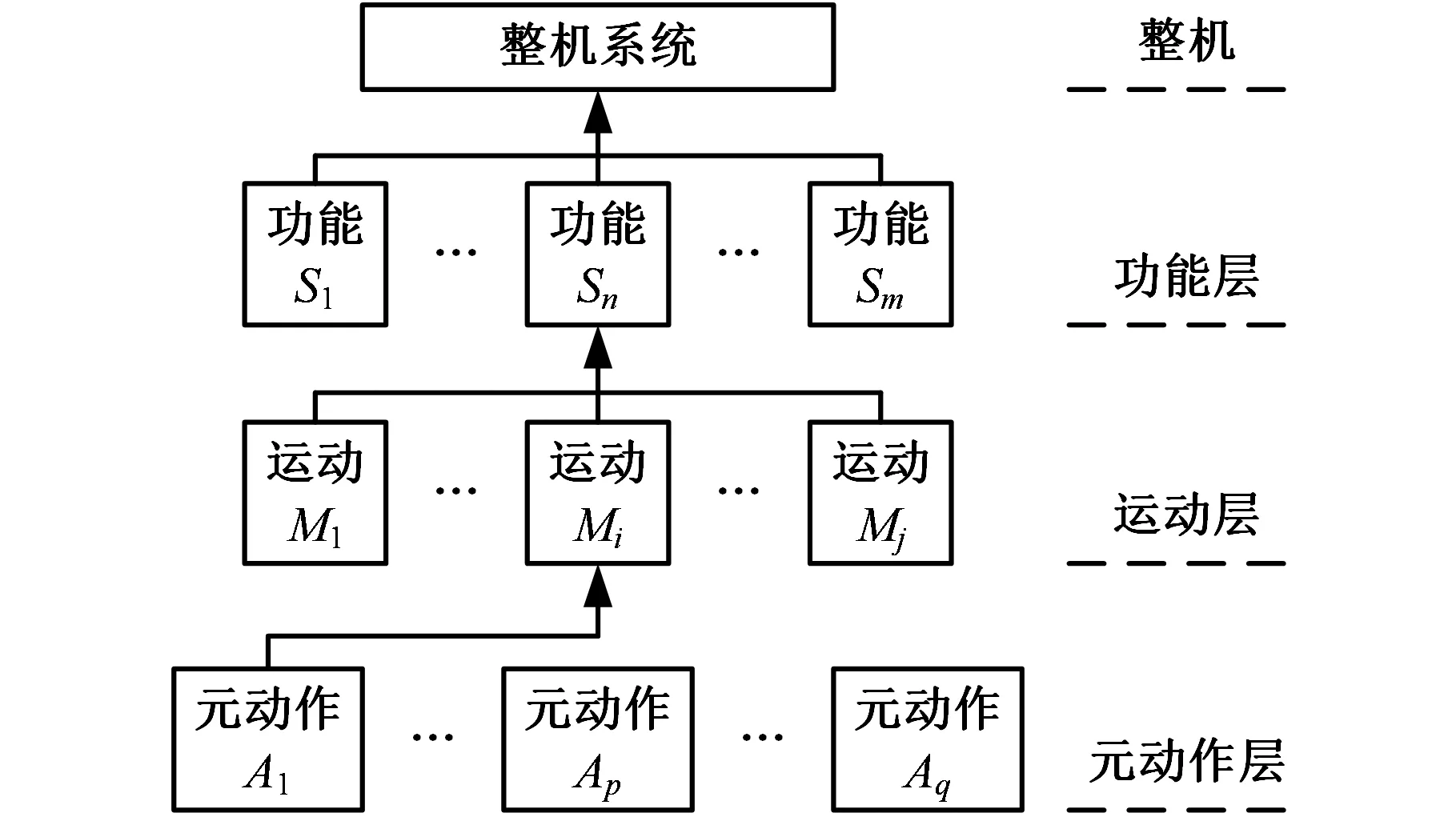
图1 机电产品FMA结构分解树Fig.1 Schematic of the FMA decomposition tree

1.2 元动作分类及其单元结构组成

元动作根据运动形式的不同分为两类：①转动元动作，如蜗杆转动元动作、齿轮转动元动作等；②移动元动作，如齿条移动元动作、直线导轨移动元动作等。

元动作单元主要由动力输入件、中间件、支撑件、紧固件和动力输出件组成，其结构模型如图2所示。上游元动作单元通过动力输出件将动力传递给当前元动作单元的动力输入件，然后经本单元的中间件传递给动力输出件，再由本单元的动力输出件传递给下游元动作单元的动力输入件，从而实现动力在机械系统中的传递。

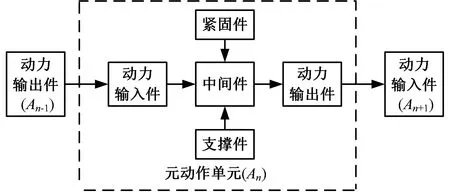
图2 元动作单元结构组成Fig.2 Structure composition of meta-action unit

1.3 元动作链介绍

元动作链(meta-action chain, MC)定义如下[15-16]：将元动作按照运动传递顺序进行有序链接，用来表示系统将运动由动力源传递到特定执行机构的元动作组合，其建立对象是一个单一的运动传递关系。

如图3所示，元动作链包含动力源、中间元动作和执行部件，中间的各个元动作相互串联，通过齿轮副、蜗轮蜗杆副等机械传动副将动力源的动力传递给执行部件。

图3 元动作链结构Fig.3 The structure of meta-action chain

1.4 元动作链运动精度机理分析

元动作链中，上游元动作的动力输出件和下游元动作的动力输入件构成传动副，将动力源的动力和运动传递给执行部件,因此，元动作执行部件的运动误差是由各个相邻元动作之间的传动副运动误差造成的。传动副的运动误差是由相互运动的动力输入件和动力输出件的安装位置偏差和本身固有误差造成的，其中，动力输入件和动力输出件的安装位置偏差仅与自身所在单元的内部零件几何误差和装配误差有关。通过上述分析可以明确元动作链的运动精度形成机理：首先，元动作单元内部的零件几何误差、装配误差等因素导致动力输入件和动力输出件的安装位置偏差；然后，动力输入件和动力输出件的安装位置偏差与本身固有误差导致相邻元动作之间传动副的运动误差；最后，传动副的运动误差导致元动作链的运动误差，形成元动作链运动误差，即机械传动系统的运动精度。

2 元动作链运动精度优化分配

2.1 元动作链运动误差建模

元动作链作为典型的机械传动系统，在综合分析其运动精度时，需要考虑各个传动副传动比的影响。元动作链的运动误差为各个传动副的运动误差折算到执行部件后的综合误差。图4所示为包含n个元动作的元动作链系统，第k-1个元动作单元的动力输出件与第k个元动作单元的动力输入件的传动比为ik,k-1。

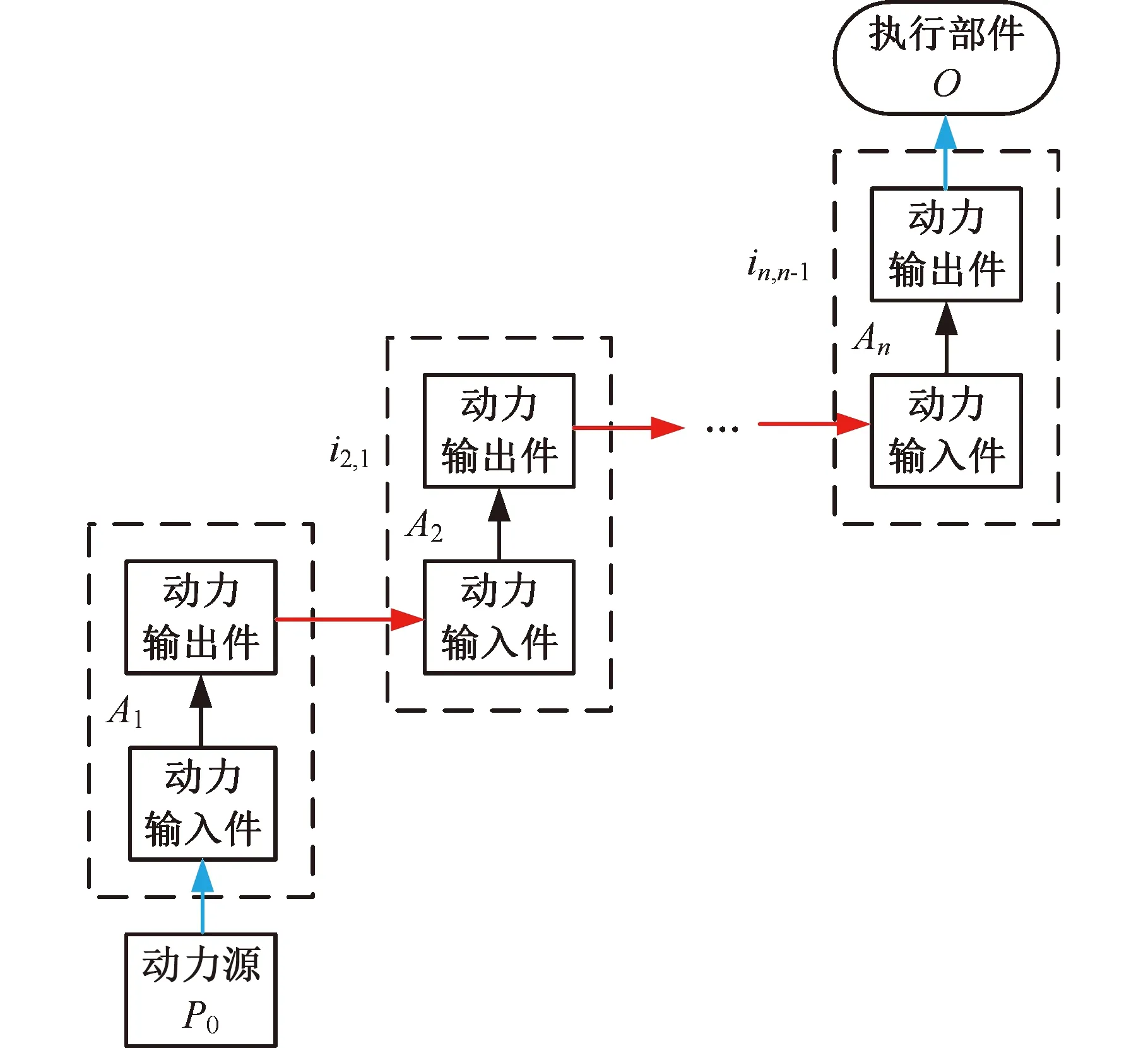
图4 元动作链动力传动系统Fig.4 Power transmission system of meta-action chain

因此，元动作链系统的运动误差为[9,17]

(1)

式中，φm-1,m为第m-1个元动作单元的动力输出件和第m个元动作单元的动力输入件组成的传动副的运动误差。

各项运动误差均为随机变量，假设各项误差均服从正态分布且相互独立，因此综合运动误差的均值μ(φMC)和标准差σ(φMC)分别为

(2)

式中，σ(*)为各误差项的标准差。

若取置信概率为99.7%，则元动作链运动误差的最大值、最小值分别为

(3)

2.2 元动作单元综合装配复杂度的计算

由元动作链运动精度机理分析可知，元动作单元中的动力输入件和动力输出件的运动误差主要由零件本身的固有误差和安装位置偏差保证。对于不同的元动作，单元组成零件的数目、结构复杂程度的不同导致生产成本具有显著差异。元动作单元结构复杂、生产制造成本较高时，如果分配的精度较高，则会极大增加生产制造的难度，导致高昂的生产成本。元动作链运动精度分配过程中，需要综合考虑元动作单元的制造难度等因素，因此，为比较不同元动作单元的制造难度，利用元动作单元综合装配复杂度对元动作单元的生产制造难度进行表征。

2.2.1综合装配复杂度分析

ELMARAGHY等[18]考虑零件材料、结构设计和规格等因素并结合机械产品装配过程特点，提出了机械产品装配复杂度模型。该模型考虑了零部件装配预处理属性和装配操作属性，先通过装配过程经验数据，得到零件装配预处理属性和装配操作属性的平均复杂度，再通过加权求得单个零件的装配复杂度，然后利用机械产品装配复杂度模型，求得整个产品的装配复杂度[19]。

对于元动作单元，影响生产制造过程复杂程度的因素包括单元零件属性、零部件配合特性、紧固件数量、装配操作、产品检测、辅助资源等因素，因此从零件预处理属性装配复杂度和零件装配操作属性复杂度进行分析[19]。

零件预处理属性装配复杂度的分析属性包括尺寸、厚度、质量、对称性、抓取难度和辅助动作。零件装配操作属性复杂度的分析属性包括对齐、插入阻力、视线、机械紧固工艺、质量检测、操作人员要求、辅助操作设备和一次装配成功率。表1、表2所示分别为装配操作属性和零件预处理属性平均复杂度。

2.2.2单元装配复杂度的建模与计算

元动作单元的装配过程复杂度指数需要综合考虑单元零部件数量、零件装配预处理属性、零件装配操作属性以及紧固件数量的影响，其计算模型为

Ca=NpCailog2Ns

(4)

式中，Ca为元动作单元的装配复杂度；Np、Ns分别为元动作单元中零件和紧固件的总数量；Cai为元动作单元的装配复杂度指数。

2.2.3单元综合复杂度指数的计算

计算元动作单元装配复杂度指数，首先需要对单元中零件的装配预处理属性和装配操作属性进行分析，计算得到零件的综合装配复杂度；然后将零件综合装配复杂度进行加权，利用式(4)得到元动作单元的综合装配复杂度。图5所示为元动作单元综合装配复杂度的计算流程。

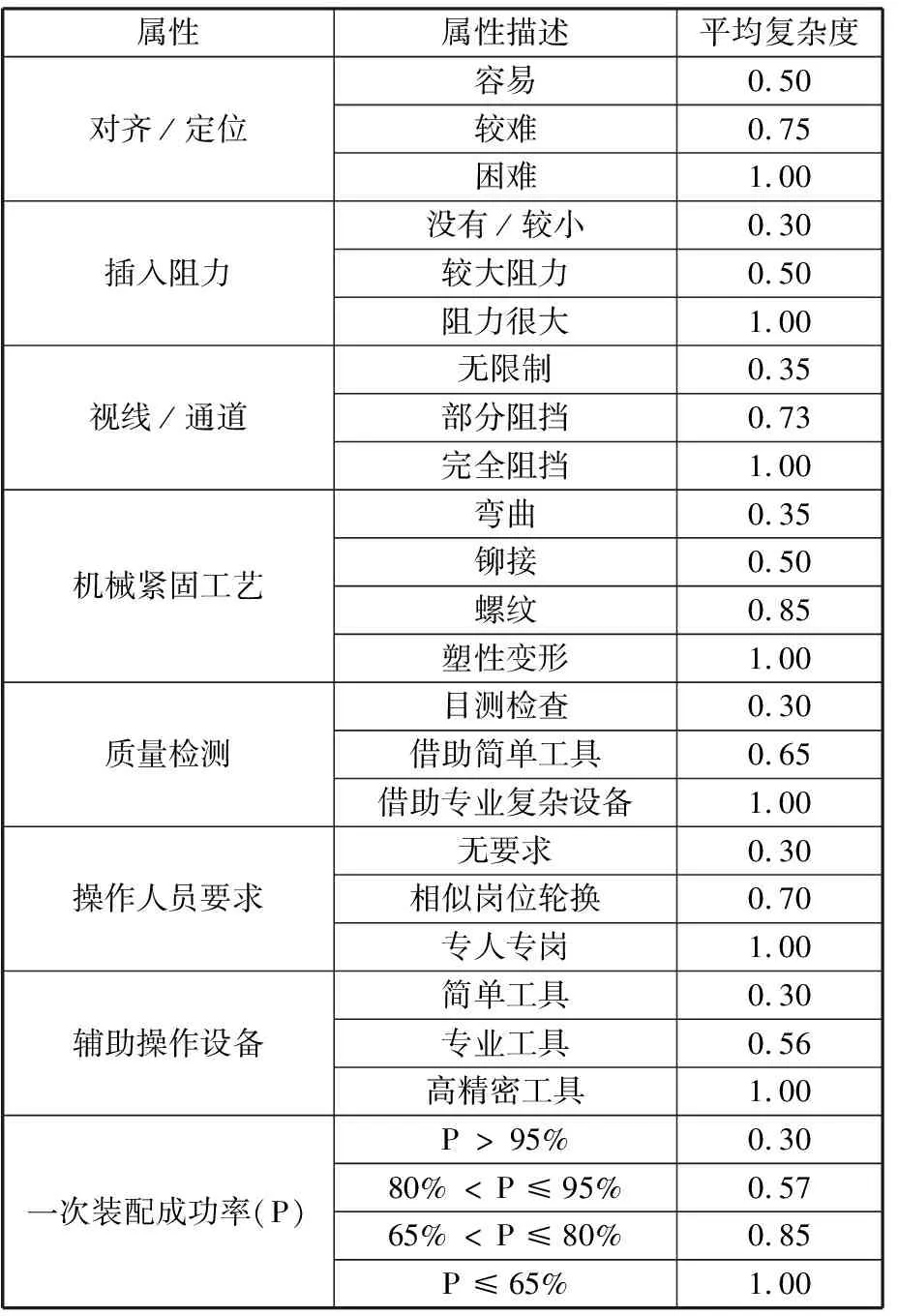
表1 零件装配操作属性复杂度

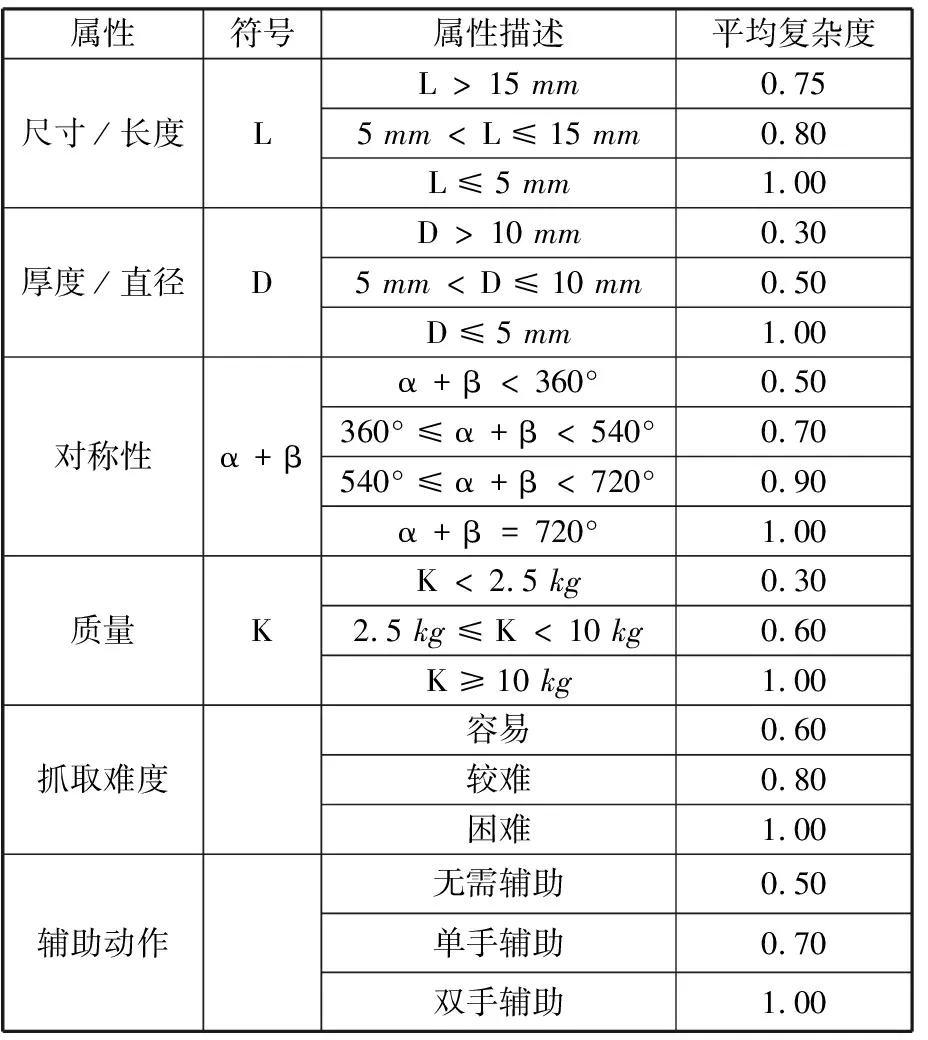
表2 零件预处理属性装配复杂度

元动作单元装配复杂度具体计算步骤如下：

(1)根据表1、表2中的数据确定元动作单元中零件的装配预处理属性复杂度和装配操作属性复杂度。

(2)分别计算零件k装配预处理属性的平均复杂度CM,k和装配操作属性的平均复杂度CO,k：

(5)

式中，CM,k,f、CO,k,f分别为零件k第f个特征的装配预处理属性复杂度和装配操作属性的特征属性复杂度；p、q分别为零件k的装配预处理属性和装配操作属性的数量。

(3)由CM,k和CO,k计算元动作单元零件k的综合装配复杂度：

Cai,k=CM,k+CO,k

(6)

(4)由元动作单元零件的装配复杂度计算单元的装配复杂度指数：

(7)

式中，np为单元特征零件的数量。

(5)将元动作单元装配复杂度指数Cai、零件总数量Np和紧固件数量Ns代入式(4)，计算得到元动作单元的综合装配复杂度Ca。

2.3 运动精度优化分配

元动作链的运动精度受元动作链各个元动作运动误差的影响。各个元动作运动误差形成元动作链的综合运动误差，即元动作链运动精度。元动作链精度分配的目的是将元动作链的运动精度分配给各个元动作，得到各个元动作单元的动力输入件和动力输出件的运动误差。

元动作链运动精度的分配包括综合运动精度的分配和传动副运动精度的分配。综合运动精度的分配是将元动作链末端执行部件的运动精度分配给相邻元动作间的传动副。传动副运动精度的分配是指将上一步分配得到的传动副运动误差分配给上游元动作单元的动力输出件和下游元动作单元的动力输入件。

通过分配元动作链的综合运动精度，得到单个元动作单元中动力输入件和动力输出件的运动误差，为元动作运动精度的优化分析奠定基础。

2.3.1元动作链综合运动精度分配

为对元动作链运动精度进行优化分配，需要综合考虑各个传动副的综合制造成本、运动精度灵敏度等因素，因此，建立的元动作链运动精度优化分配模型不仅包括设计变量和目标函数，还包括成本函数和鲁棒函数[20]。

(1)设计变量。元动作链包括n个传动副，以每个传动副的运动误差(最小值为0，最大值通过元动作链运动精度的标准差确定)的标准差为设计变量，即

(8)

式中，σ[φMC]为元动作链运动误差的标准差；σ(φ′m-1,m)为元动作单元之间传动副的运动误差的标准差。

(2)目标函数。将各个传动副运动误差的分配值代入元动作链运动误差模型，计算得到元动作链的运动误差，然后将计算得到的元动作链运动误差与设计值的差值作为目标函数：

(9)

(3)成本函数。元动作链运动精度优化分配过程中，生产成本主要是各个元动作单元的综合装配成本。每个元动作单元的结构、组成零部件的数目和种类等均不相同，因此用单元综合装配复杂度对成本进行度量，则成本函数为

(10)

(11)

式中，Ca,m-1、Ca,m-1分别为第m和m-1 个元动作单元的综合装配复杂度；ρm-1,m为传动副装配成本加权系数，通过各个单元的综合装配复杂度计算获得。

(4)鲁棒函数。为将各个传动副运动误差的不确定性对元动作链运动精度的影响最小化，通过灵敏度分析，设计了如下鲁棒函数：

(12)

Δ[σ(φm-1,m)]=0.2σ(φm-1,m)

优化模型以成本和鲁棒性为目标，是多目标优化问题，为降低问题分析的难度，将多目标优化问题转化为单目标优化问题，即将成本和鲁棒性进行归一化处理：

(13)

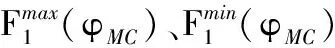
通过式(8)～式(13)得到元动作链综合运动精度优化分配模型：

(14)

式中，β1、β2为权重系数，表示决策者对成本和鲁棒性的偏好程度，0≤β1，β2≤1，β1+β2=1。

式(14)为典型的单目标优化问题，利用多岛遗传算法[21]进行求解，可得到各个传动副的运动误差的分配值。

2.3.2传动副运动精度优化分配

传动副中的零件属于不同的元动作单元，因此需要将传动副的运动精度再次进行分配，得到相邻元动作单元中动力输入件和动力输出件的运动误差。设第m-1个元动作单元和第m个元动作单元之间的传动副的运动误差为φm-1,m，相互配合的上游元动作动力输出件和下游元动作动力输入件的运动误差分别为φm-1和φm，则通过综合精度分配可得

φm-1,m=φm-1+φm

(15)

传动副的运动误差的均值和标准差分别为

(16)

同样，以传动副的运动误差为分配目标，得到上游元动作单元动力输出件和下游元动作单元动力输入件的允许运动误差。考虑各个元动作单元制造装配成本和灵敏度等因素，建立传动副运动精度优化分配模型，该模型同样包括设计变量、目标函数、成本函数和鲁棒函数。

(1)设计变量。传动副中，上游元动作单元的动力输出件和下游元动作单元的动力输入件的运动误差(最小值为0，最大值为传动副允许最大运动误差的标准差)的标准差为设计变量：

(17)

(2)目标函数。以传动副最大允许运动误差的标准差为分配目标，根据式(16)得到的目标函数为

(18)

(3)成本函数。动力输出件和动力输入件的运动误差受元动作单元内部零件误差和装配误差的影响，因此用单元装配复杂度对相邻元动作单元的成本进行度量，则成本函数为

(19)

(20)

式中，ηm-1、ηm分别为元动作单元Am-1和Am的成本加权系数。

(4)鲁棒函数。为减小上游元动作单元的动力输出件和下游元动作单元的动力输入件运动误差的不确定性对传动副运动精度的影响，通过灵敏度分析，设计了鲁棒函数：

(21)

Δ[σ(φ′m-1)]=0.1σ(φ′m-1)Δ[σ(φ′m)]=0.1σ(φ′m)

采用式(13)的方法，对成本函数和鲁棒函数进行归一化处理：

(22)

通过式(17)～式(22)，得到传动副运动精度优化分配模型：

(23)

式(23)同样为单目标优化问题，可以利用多岛遗传算法进行求解，最终得到相邻元动作单元动力输出件和动力输入件的允许运动误差。

2.4 元动作链运动精度优化分配流程

元动作链的运动精度优化分配如图6所示。具体如下：

(1)分析元动作链结构，确定元动作链运动精度指标，建立运动误差模型。

(2)确定设计变量，建立优化分析模型的目标函数、约束函数和设计变量。

(3)利用优化算法进行分析计算，得到元动作链中各个传动副的运动误差分配值。

(4)以φm-1,m为分配目标，进行优化分配。

(5)建立φm-1,m的优化分配数学模型，该模型包括确定目标函数、约束函数和设计变量。

(6)利用优化算法进行分析计算，得到元动作单元Am-1的动力输出件和元动作单元Am的动力输入件的运动误差的分配值，最后得到元动作运动精度。

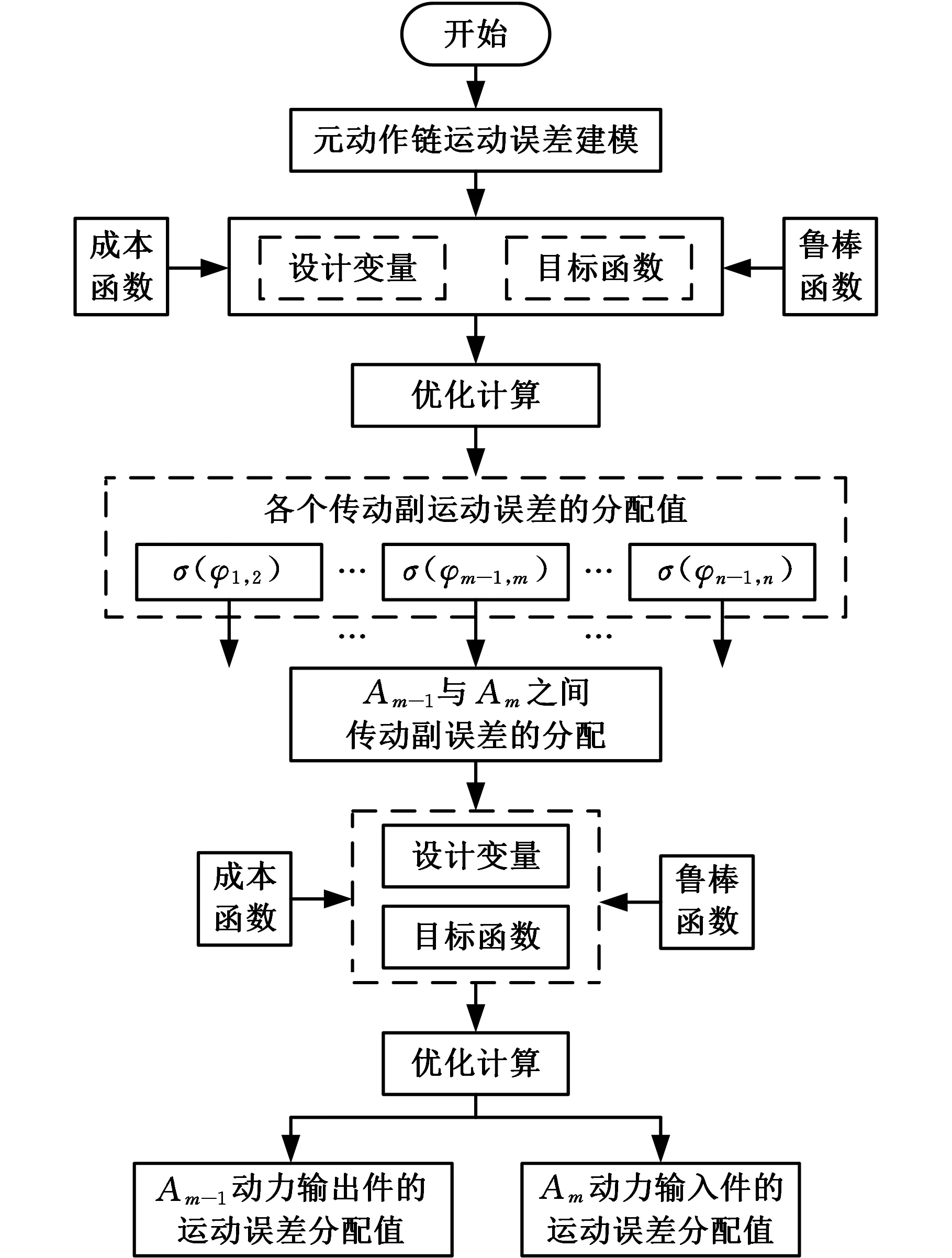
图6 元动作链运动精度优化分配Fig.6 Optimal allocation of meta-action chainkinematic accuracy

3 实例分析

利用FMA结构化分解方法对某型号数控磨床进行结构化分解，如图7所示。以C轴数控回转工作台为主进行运动分解，得到了2个分运动以及分运动包含的元动作和元动作链[22]。

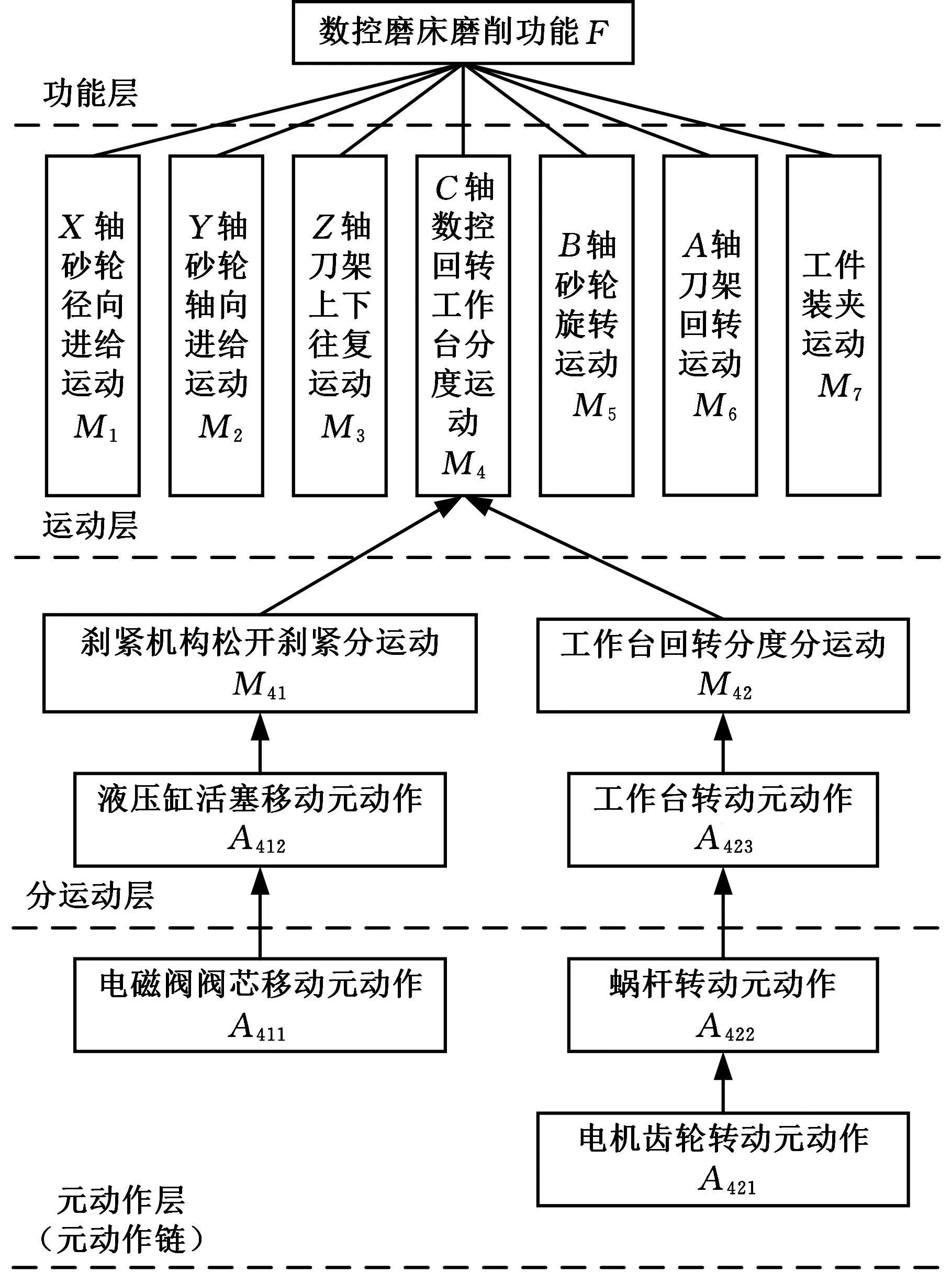
图7 数控磨床FMA结构化分解Fig.7 FMA structured decomposition for a CNCgrinding machine

数控回转工作台主要由箱体、电机齿轮、输入齿轮、蜗杆、蜗轮、工作台和刹紧机构等部分构成，是数控磨床重要的功能部件，其回转定位精度对数控磨床的加工精度有重要影响，因此利用所述方法对数控回转工作台传动系统的运动精度进行优化分配。

3.1 数控回转工作台结构分析

对数控回转工作台的转动元动作链进行运动精度优化分配，首先需要明确该元动作链的结构组成，以及数控回转工作台的工作过程。

工作台回转运动工作过程：电机轴输出的转矩带动电机齿轮转动，通过电机齿轮与蜗杆右端输入齿轮的啮合实现蜗杆的转动，通过蜗杆与蜗轮的啮合实现蜗轮的转动，工作台与蜗轮固连在一起，最终实现工作台的回转运动。

工作台刹紧工作过程：工作台后端安装刹紧片，工作台刹紧腔通入压力油后，活塞压紧刹紧片，实现工作台的刹紧。工作台刹紧腔的压力油卸压后，活塞在弹簧的作用下，由压紧位置回到脱开位置，松开工作台。

3.2 工作台回转元动作链

通过数控磨床FMA分解和工作台回转运动过程的分析，并结合元动作链的概念，得到转台回转元动作链，如图8所示。该元动作链动力传递路径为电机齿轮转动元动作-蜗杆转动元动作-工作台转动元动作，动力源为电机，执行部件为工作台。

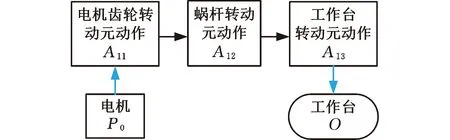
图8 工作台回转运动元动作链Fig.8 Meta-action chain of worktable rotary element

电机齿轮转动元动作的动力输入件为齿轮轴，动力输出件为电机齿轮；蜗杆转动元动作的动力输入件为输入齿轮，动力输出件为蜗杆；工作台转动元动作的动力输入件为蜗轮，动力输出件为工作台。建立该元动作链动力传动系统，如图9所示，其中i2,1=90，i3,2=2。

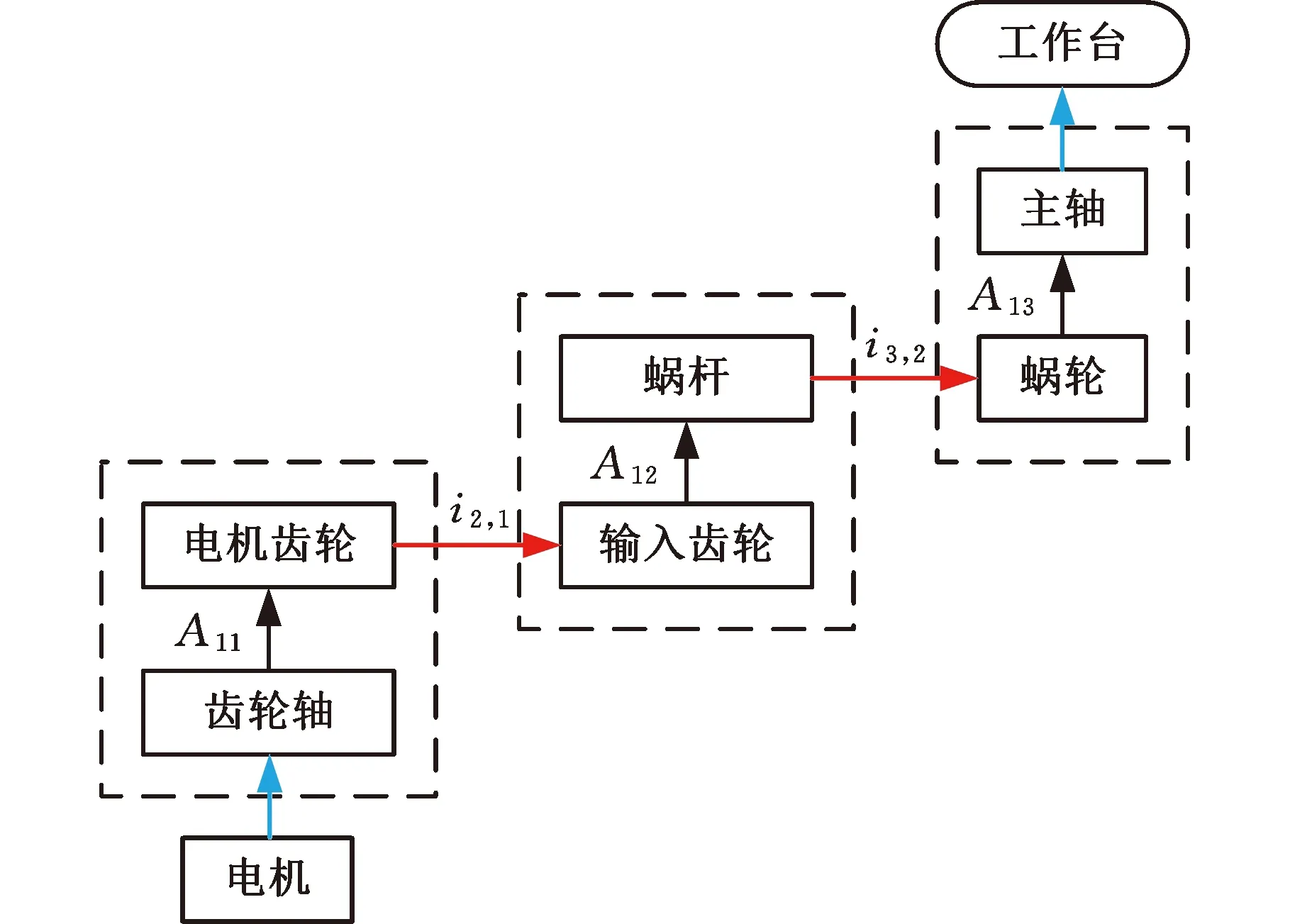
图9 转台回转元动作链动力传递图Fig.9 Power transfer process of meta-actionchain of turntable

3.3 数控转台运动精度优化分配

由数控回转工作台的设计要求可知，工作台的回转定位精度为30″，将此指标作为数控回转工作台的运动精度指标进行优化分配。

分析转台回转元动作链中各个元动作单元的结构特点和零件组成，利用2.2节所述方法，计算得到电机齿轮转动元动作单元、蜗杆转动元动作单元和工作台转动元动作单元的综合装配复杂度，即Ca,A1=71.21，Ca,A2=205.86，Ca,A3=802.85。

根据式(9)建立工作台回转定位精度与齿轮副和蜗轮蜗杆副的运动误差的计算模型：

(24)

以齿轮副和蜗轮蜗杆副的运动误差的标准差为设计变量，其取值范围由式(8)计算得到：

(25)

通过式(14)建立数控转台回转元动作链运动精度优化分配模型：

(26)

对式(26)进行分析求解，得到各个传动副运动误差的标准差分配值，然后根据式(3)得到传动副的运动误差。分配过程中，成本和鲁棒性决定了元动作链的综合制造成本和运动精度的稳定性，因此决策者通过选择不同的权重系数(β1,β2)对精度分配结果进行综合权衡。为分析不同决策对元动作链运动精度分配结果的影响，分析计算了β2取不同值时齿轮副运动误差φ1,2和蜗轮蜗杆副运动误差φ2,3的分配情况。

蜗杆转动元动作单元和工作台转动元动作单元的结构比较复杂，综合装配复杂度较大，而电机齿轮转动元动作单元的综合装配复杂度较小,因此，提高蜗轮蜗杆副的运动精度需要花费的成本比提高齿轮副的运动精度花费的成本高很多。蜗轮蜗杆副的运动误差会直接传递给工作台，其灵敏度较高；齿轮副的运动误差受蜗轮蜗杆副的传动比(i=90)的影响，其灵敏度较低。

因此，若重点考虑综合成本，则蜗轮蜗杆副应该分配较大的运动误差，齿轮副分配较小的运动误差；若重点考虑鲁棒性因素，则蜗轮蜗杆副应该分配较小的运动误差，齿轮副分配较大的运动误差。

图10所示为齿轮副和蜗轮蜗杆副的分配误差随决策者偏好的变化。当决策者比较重视成本即β2较小时，φ2,3取值较大，φ1,2取值较小。当决策者比较重视鲁棒性即β2较大时，φ2,3取值较小，φ1,2取值较大。

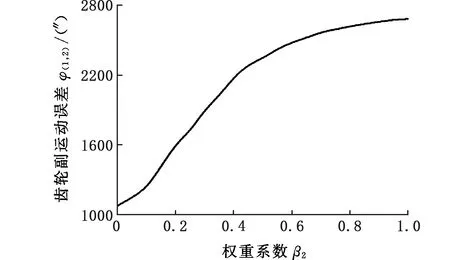
(a)φ1,2随决策偏好的变化

(b)φ2,3随决策偏好的变化图10 决策者偏好对元动作链精度分配的影响Fig.10 Influence of decision maker’s preference onprecision allocation of meta-action chain

以φ1,2和φ2,3(其标准差分别为σ(φ1,2)和σ(φ2,3))为分配对象，利用式(17)分别得到电机齿轮、蜗杆右端输入齿轮、蜗杆以及蜗轮运动误差的标准差范围：

(27)

(28)

根据式(23)分别建立齿轮副和蜗轮蜗杆副的运动精度优化分配模型：

(29)

(30)

计算式(29)、式(30)，并考虑决策者对成本和鲁棒性的偏好程度，求解得到电机齿轮、蜗杆右端输入齿轮、蜗杆和蜗轮的运动误差的标准差，然后计算得到其运动误差的分配值。

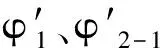
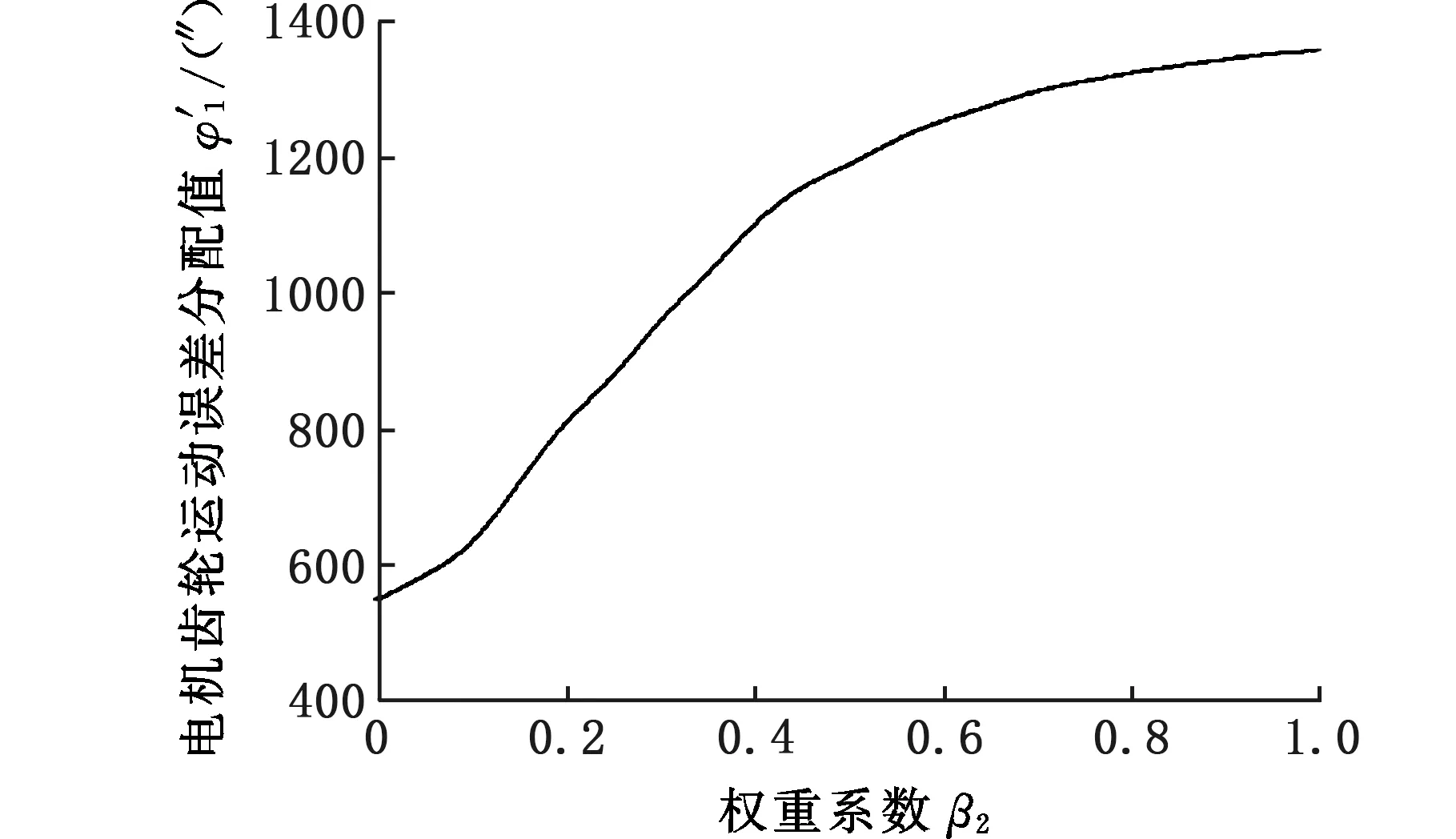
(a)φ′1随决策偏好的变化

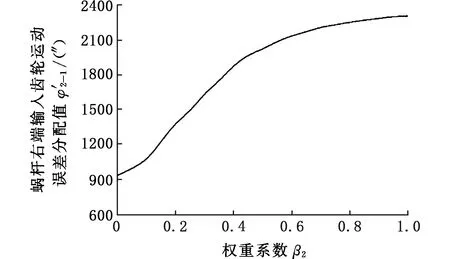
(b)φ′2-1随决策偏好的变化

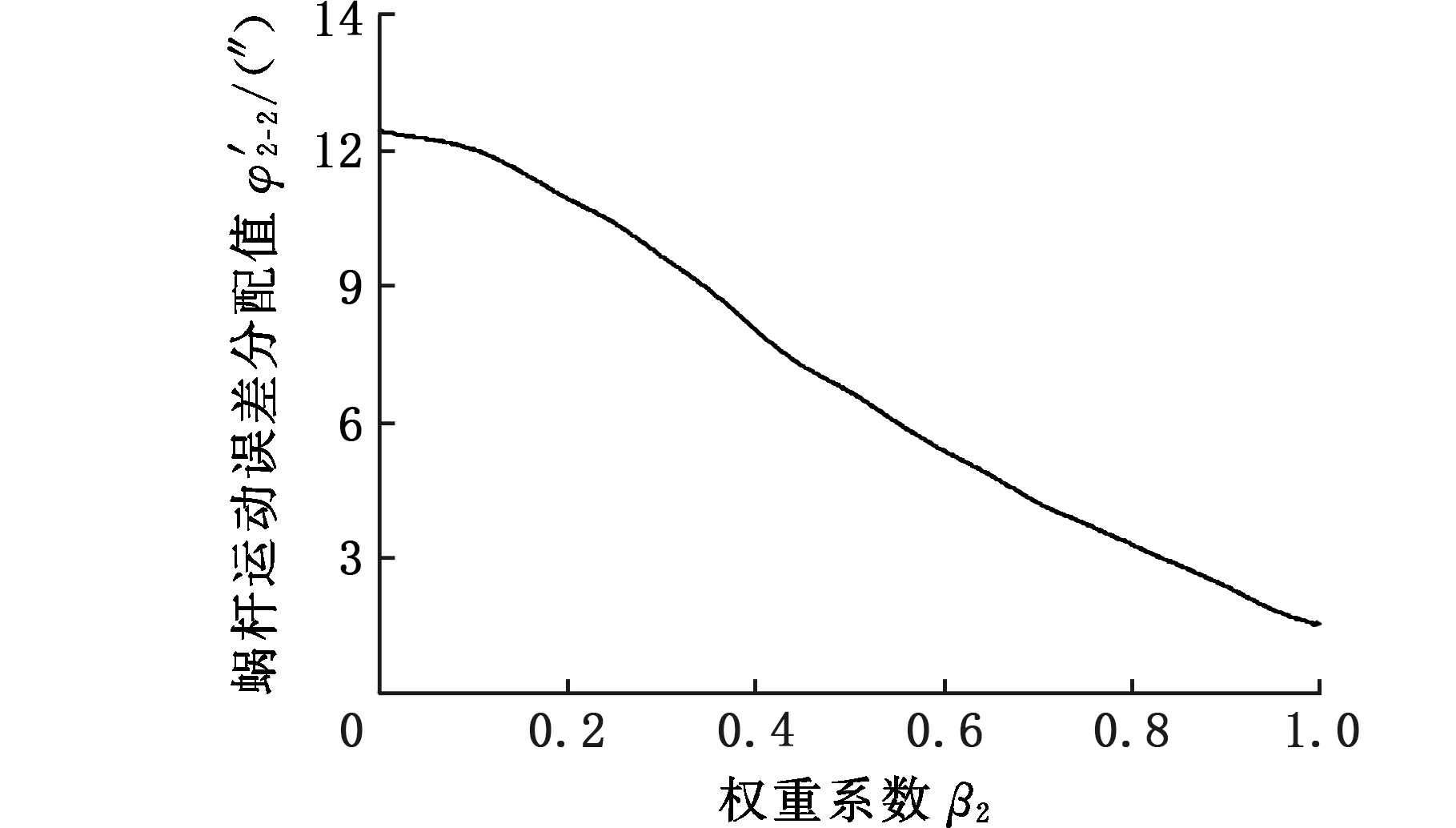
(c)φ′2-2随决策偏好的变化

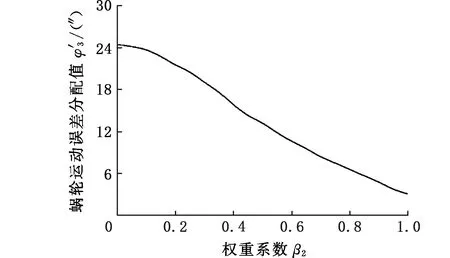
(d)φ′3随决策偏好的变化

4 结论

(1)从机械传动系统运动精度形成机理出发，对机械传动系统运动误差进行分析，建立了运动精度优化分配模型。该模型以机械传动系统运动误差的形成过程为基础，分析结果更加合理。

(2)通过分析元动作单元的综合装配复杂度，建立了成本函数；通过元动作链运动精度的灵敏度分析，建立了机械传动系统运动精度的鲁棒函数。分析并得到成本和鲁棒性对分配结果的影响规律。

本文方法提高了运动精度分配的合理性，但在成本函数建模分析过程中，仅仅考虑了元动作单元的综合装配复杂度。实际工程中，元动作单元的维修性以及维修过程的成本对运动精度的分配也有重要影响。因此，在今后的研究中，需要综合考虑设计、制造和维修等因素，建立面向全生命周期的成本函数模型，使机械传动系统的运动精度分配更加合理，对实际生产过程提供更好的指导作用。