利用弹性网络算法求解大型三坐标测量机几何误差的方法

陈洪芳 孙梦阳 高 毅 石照耀 王帼媛 路伟光 宋辉旭

1.北京工业大学北京市精密测控技术与仪器工程技术研究中心，北京，1001242.中国航空工业集团公司北京航空精密机械研究所，北京，100076

0 引言

航空发动机、大型汽轮机、风力机、汽车、大型舰船等大型先进制造装备的核心关键部件如叶片、大齿轮、大箱体、大主轴等的精密测量，对保障先进制造装备性能至关重要。为使我国成为大型先进制造装备的制造强国，必须全面提升叶片、大齿轮等核心机械基础部件的制造与测试水平。而高精度大型三坐标测量机是先进高端制造装备领域大型关键核心部件高精度检测的有效手段[1-2]。

大型三坐标测量机(coordinate measuring machine，CMM)测量空间大、各运动部件质量大，且易受环境温度变化影响[3-5]，其精度提高与中小型CMM相比非常困难。完全通过提高大型CMM制造的精度、严格控制环境条件来实现高测量精度是很困难的，成本也高。CMM制造中除了机械主机、标尺、导轨、驱动机构、平衡部件、测头等硬件基础保证精度外，21项几何误差的高精度、高效补偿是保证CMM整体性能的先决条件。

传统方法修正大型CMM空间几何误差的效率有限，实物基准体积大、较为笨重且难以加工[6-7]。激光跟踪仪作为一种面向现场的便携式三维坐标测量仪器，与其他CMM的几何误差修正技术相比，效率高、操作方法简单，但其角度测量的精度有限，且随着测量距离的增大，角度的测量不确定度更大，因此激光跟踪仪在大型CMM空间几何误差修正中受限。激光追踪仪采用基准球设计，机械旋转轴的偏差对精度影响较小，且仅采用长度量，因此精度较高，达到了0.2 μm + 0.3 μm/m。激光追踪仪更适合用于大型CMM空间体积误差的测量。

对于三坐标测量机几何误差的求解，传统的方式均基于体积误差与单轴几何误差之间的关系模型，该模型数据利用率低、算法精度低且耗时长。ZHANG等[8]利用激光跟踪仪转站测量CMM的体积误差，并对体积误差进行分解得到几何误差，该方法求解几何误差的效率较低，且数据利用率不高。基于激光追踪仪多站位测量技术有利于CMM体积误差测量效率的提高，但是基于准刚体模型求解几何误差过程中存在多重共线问题。

弹性网络(elastic net)算法由斯坦福大学于2005年提出[9]，是一种使用L1、L2范数作为先验正则项训练的线性回归模型，结合了 LASSO筛选重要变量的特性和岭回归防止多重共线性的优点[10]。

本文利用激光追踪仪多站位测量技术，提出了基于弹性网络算法求解CMM几何误差的方法，解决了该方程组多参数求解的多重共线问题，相较于传统的单项几何误差测量及补偿，该方法的多参数求解效率更高；此外，相较于传统的大型CMM几何误差修正方法，该方法所采用的激光追踪仪多站位测量技术更高效，操作更便捷。

1 CMM几何误差求解方法

基于激光追踪多站位测量技术对CMM体积误差进行测量，利用L-M(Levenberg-Marquard)算法求解其目标方程，实现激光追踪仪站位自标定及体积误差的高精度测量。基于符合FYXZ型CMM的准刚体模型，建立CMM体积误差与几何误差的关系模型，整理得到求解几何误差的目标方程组。为解决目标方程组多重共线问题，利用弹性网络算法求解CMM的几何误差。

1.1 激光追踪多站位测量系统工作原理

建立图1所示的激光追踪多站位测量系统。将激光追踪仪分时转站放置在CMM测量平台的不同位置，猫眼被固定于CMM测头位置，猫眼随CMM的测头移动。从激光追踪仪发出的激光经猫眼反射后，再经过激光追踪仪内固定的标准球反射后作为测量光束，与参考光束形成干涉，以实现激光追踪仪的跟踪测距。

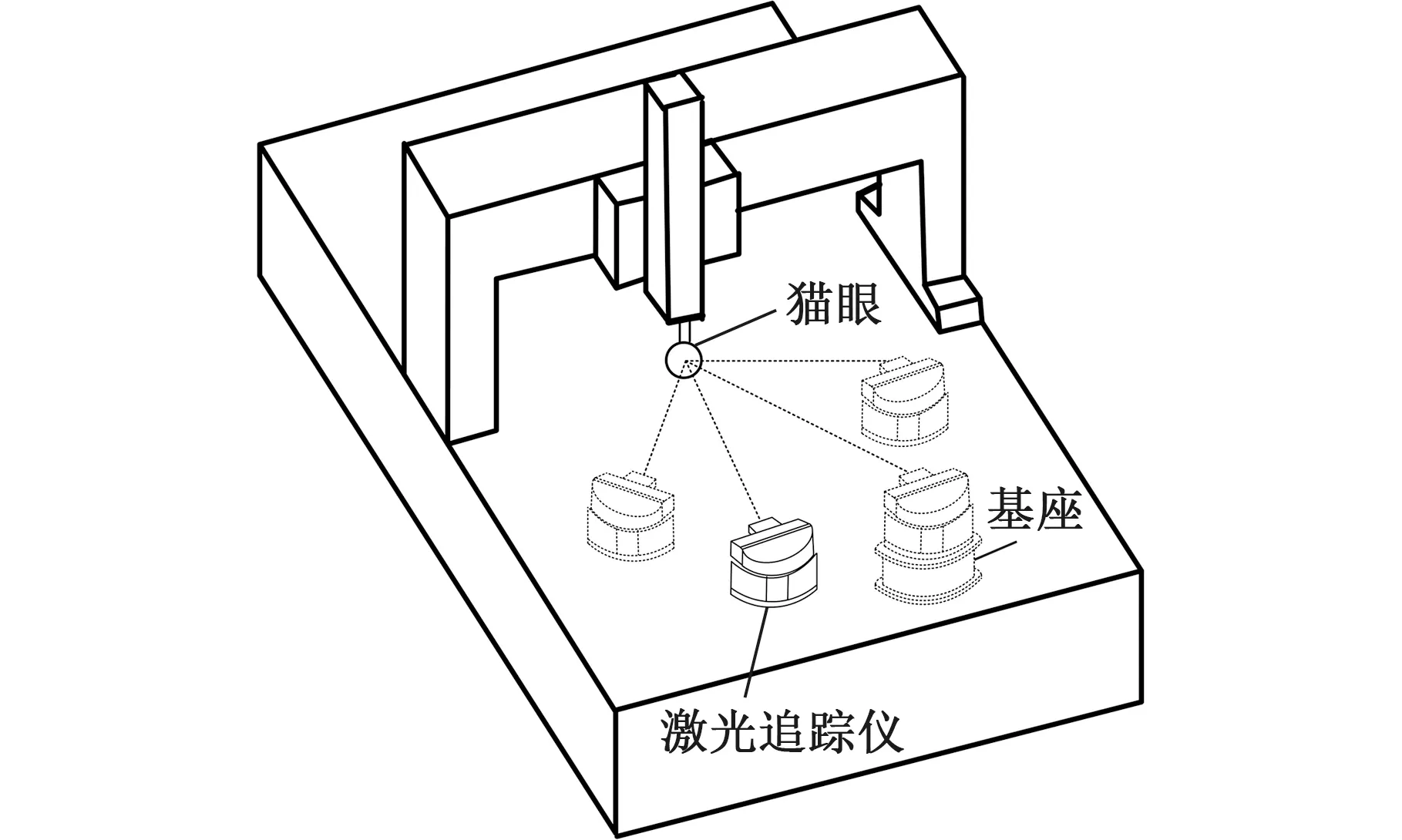
图1 激光追踪多站位测量系统Fig.1 Laser tracing multi-station measurement system

1.2 基于L-M算法测量CMM体积误差的原理

根据激光追踪仪的测距原理，激光追踪多站位测量模型可由下式表示：

Fi(Xj,Yj,Zj,dj)=

(1)

其中,i为测量点个数，i=1,2,…,n；j为追踪仪站位个数，j=1,2,…,m；(Xj,Yj,Zj) 为激光追踪仪站位坐标；(xi,yi,zi) 为待测点理论坐标；dj为激光追踪仪站位到待测初始测量点的距离；lij为激光追踪仪在第j个站位测量第i个待测点时测量的相对干涉长度。

利用L-M算法求解出激光追踪仪站位坐标Pi(Xj,Yj,Zj)和dj。激光追踪仪站位自标定利用全球定位系统(GPS)建立模型，避免了坐标系的转换；在求解模型时采用L-M算法解算非线性方程组，有效提高了站位自标定的精度[11]。

基于L-M算法求解测量点的实际坐标,与式(1)相似，测量模型如下所示：

Fj(xi,yi,zi)=

(2)

将求解的激光追踪仪站位坐标Pi(Xj,Yj,Zj)和dj作为已知参数代入式(2)中，利用L-M算法对待测点实际坐标Ai(x′i,y′i,z′i)求解。

记待测点理论坐标为Ai(xi,yi,zi)，则CMM体积误差为待测点实际坐标与理论坐标之差为

(3)

1.3 FYXZ型CMM准刚体模型建模

以FYXZ型三坐标测量机为例，建立准刚体模型如下[12]：

Δx=δx(x)+δx(y)+δx(z)+(z+z1)εy(x)-
y1εz(x)+(z+z1)εy(y)-y1εz(y)+
z1εy(z)-y1εz(z)-zαxz

(4)

Δy=δy(x)+δy(y)+δy(z)-(z+z1)εx(x)+
x1εz(x)-(z+z1)εx(y)+(x+x1)εz(y)-
z1εx(z)+x1εz(z)-xαxy-zαyz

(5)

Δz=δz(x)+δz(y)+δz(z)+y1εx(x)-
x1εy(x)+y1εx(y)-(x+x1)εy(y)+
y1εx(z)-x1εy(z)

(6)

其中，A1(x1,y1,z1)为待测初始点坐标;(x,y,z)为CMM相对初始点的位移;(Δx,Δy,Δz)为待测点体积误差;δx(x)、δy(x)、δz(x)为x轴位移误差；εx(x)、εy(x)、εz(x)为x轴旋转误差；δx(y)、δy(y)、δz(y)为y轴位移误差；εx(y)、εy(y)、εz(y)为y轴旋转误差；δx(z)、δy(z)、δz(z)为z轴位移误差；εx(z)、εy(z)、εz(z)为z轴旋转误差；αxy、αxz、αyz为垂直度误差。

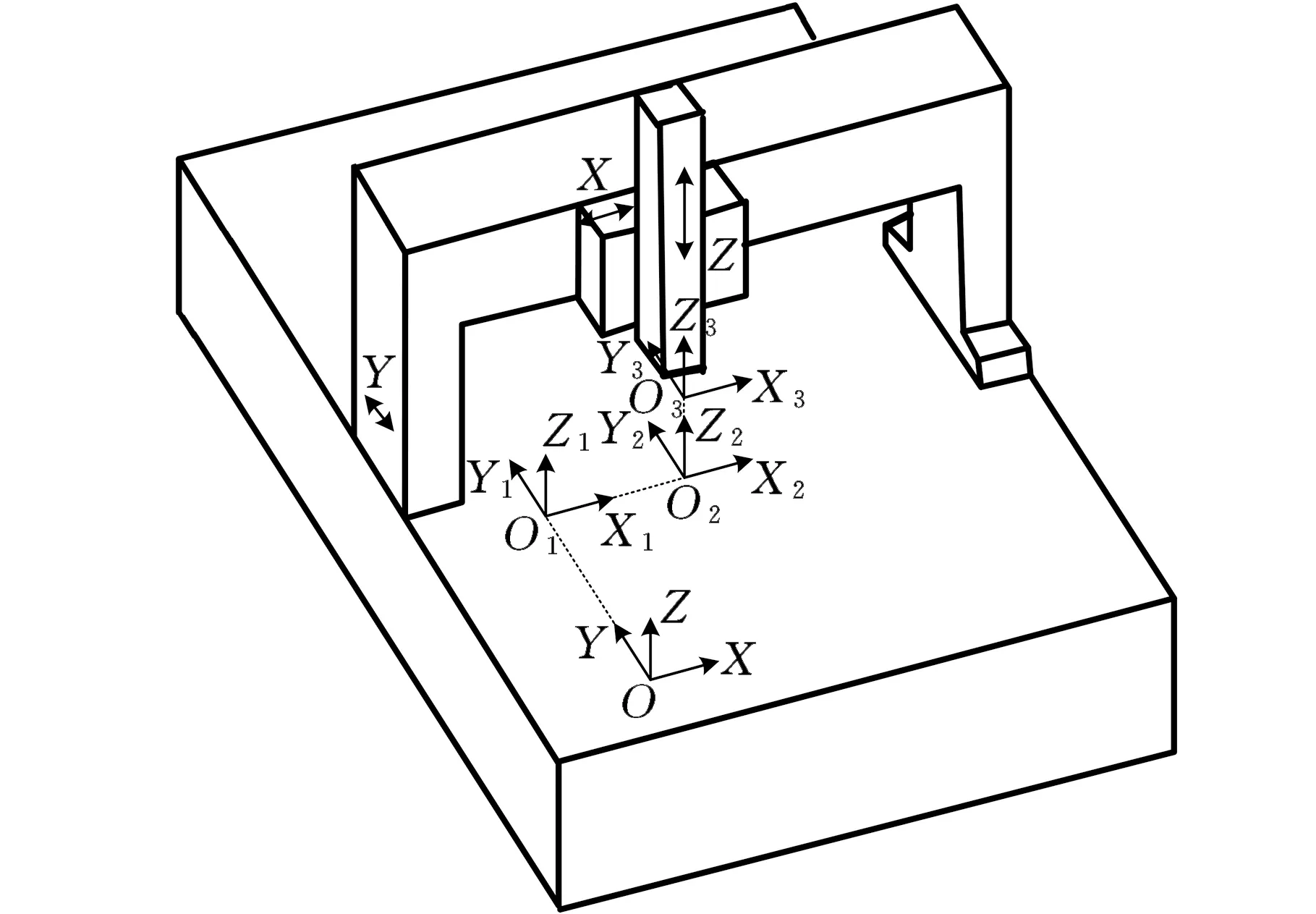
图2 三坐标测量机结构示意图Fig.2 Structure diagram of coordinatemeasuring machine

FYXZ型三坐标测量机结构如图2所示。根据上述准刚体模型，结合待测点个数及误差个数建立体积误差与几何误差之间的方程组。令CMM测量空间内任意待测点Ai(xi,yi,zi)到第一个待测点A1(x1,y1,z1)3个坐标轴的位移分别为xi1=xi-x1,yi1=yi-y1,zi1=zi-z1，代入CMM的准刚体模型式(4)～式(6)中，得到

Aixi=bi

(7)

其中

bi=[ΔxiΔyiΔzi]T

(8)

xi=(δx(x),δy(x),δz(x),εx(x),εy(x),
εz(x),δx(y),δy(y),δz(y),εx(y)，εy(y),
εz(y),δx(z),δy(z),δz(z),εx(z),εy(z),
εz(z),αxy,αxz,αyz)T

(9)

Ai=

(10)

(11)

式中，δx(x)表示由x轴的定位误差构成的矩阵，其大小与x轴所规划的测量范围及步长大小有关，其余几何误差矩阵均与δx(x)有相同含义；Exx1表示δx(x)对应的系数矩阵，长度与x轴规划的测量范围及步长大小有关，其余单位矩阵的定义均与Exx1相同；(z+z1)1表示εy(x)的系数矩阵，因此(z+z1)1的大小与εy(x)相同，其余系数矩阵均有相同的含义。

设方程组所包含几何误差的个数为f个，共n个待测点，每个待测点对应一个式(10)，整理方程组即可得到式(11)。

1.4 基于弹性网络算法的CMM几何误差求解

由于式(11)系数矩阵奇异，故采用弹性网络算法对其求解，优化目标如下：

(12)

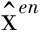
采用坐标下降法求式(12)。对系数矩阵A进行零均值标准化，将由体积误差组成的矩阵b中心化，即

(13)

式中，u为方程式个数，u=1,2,…,3n；n为待测点个数；p为第p个几何误差个数，p=1,2,…,f。

根据弹性网络公式(式(12))构造惩罚函数:

(14)

式中,λ1>0；λ2>0。

令δ=λ1/(λ1+λ2)(在计算过程中需选取合适的δ值)，δ为惩罚因子，λ=λ1+λ2，则式(14)可写为

(15)

对L(x)求偏导有

(16)

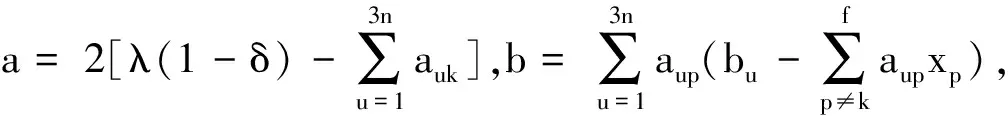
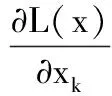
(17)

根据最小二乘原理，令式(17)为0，迭代解得CMM几何误差为

(18)

由式(10)可以看出，旋转误差εz(x)、εx(z)、εy(z)、εz(z)的系数均为初始测量点的坐标值A1(0,0,0)，故εz(x)、εx(z)、εy(z)、εz(z)4项几何误差通过准刚体模型无法求解。因此利用体积误差与单轴几何误差的关系模型进行求解。

由于6种几何误差分量和位移x的影响，实际x滑动坐标系的位姿发生了变化。利用4×4齐次变换矩阵可以表征参考坐标系与实际x轴滑动坐标系之间的关系。体积误差可由下式求得：

(19)

将通过弹性网络算法求解得到的δx(x)、δy(x)、δz(x)、εx(x)、εy(x)及体积误差代入式(19)，可以求得εz(x)。

体积误差与z轴几何误差的关系如下所示：

(20)

将通过弹性网络算法求解得到的δx(z)、δy(z)、δz(z)及体积误差代入式(20)，基于最小二乘原理利用QR分解对其进行求解，获得旋转误差εx(z)、εy(z)、εz(z)。

2 实验

2.1 搭建实验系统

搭建基于激光追踪仪的多站位测量系统，如图3所示。本实验使用海克斯康LaserTracer激光追踪仪，将激光追踪仪分时转站放置在CMM测量平台的不同位置进行测量。共规划4个不同的激光追踪仪站位。猫眼固定在CMM测头位置，并跟随CMM移动。CMM的测量范围为1500 mm×2500 mm×1000 mm。拟规划待测点的空间范围为1400 mm×2400 mm×1000 mm，在激光追踪仪的测量软件中规划测量路径，共规划待测点188个，如图4所示。

图3 激光追踪测量系统Fig.3 Laser tracer measurement system

图4 测量点分布Fig.4 Distribution of measuring points

当激光追踪仪位于第一个站位P1时，CMM及猫眼按规划路径移动，激光追踪仪追踪并采集规划的188个待测点到P1的相对干涉测长距离。为获得高精度的测量数据，激光追踪仪系统将188个待测点位置往返采集，即除最后一点外其他测量点均获得两组数据(共得到375个测量数据)，并进行对比，以确保其测量误差在允许范围内。重复以上过程，分时转站4个站位测量。实验过程中共采集1500个激光追踪仪干涉测长值。

2.2 实验结果

2.2.1激光追踪仪站位自标定

激光追踪仪的精度为亚微米级，本文搭建的激光追踪仪多站位测量系统的精度需求为亚微米级，即ε=10-4。将实验所得的干涉测长值及CMM待测点的理论位置坐标代入激光追踪多站位测量模型(式(1))中，利用L-M算法对其进行求解，经过多次迭代得出基于CMM坐标系的激光追踪仪站位坐标Pj(Xj,Yj,Zj) 以及激光追踪仪站位到测量起始点距离dj，如表1所示。

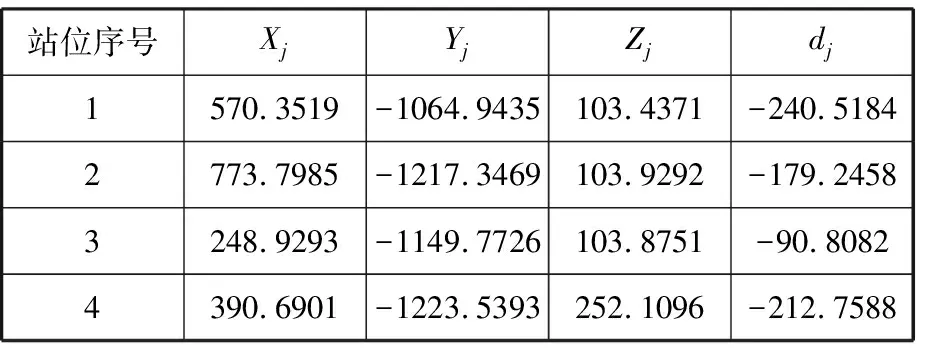
表1 激光追踪仪站位坐标及测量起始点距离

2.2.2CMM体积误差测量

CMM的体积误差为待测点实际位置坐标与理论位置坐标之差。将2.2.1节中求得的激光追踪仪站位坐标和激光追踪仪站位到测量起始点的距离代入激光追踪多站位测量模型(式(2))中，利用L-M算法对其进行求解，经过多次迭代得出CMM待测点的实际位置坐标,与理论位置坐标比较即可得到CMM的体积误差，实验结果如图5所示。

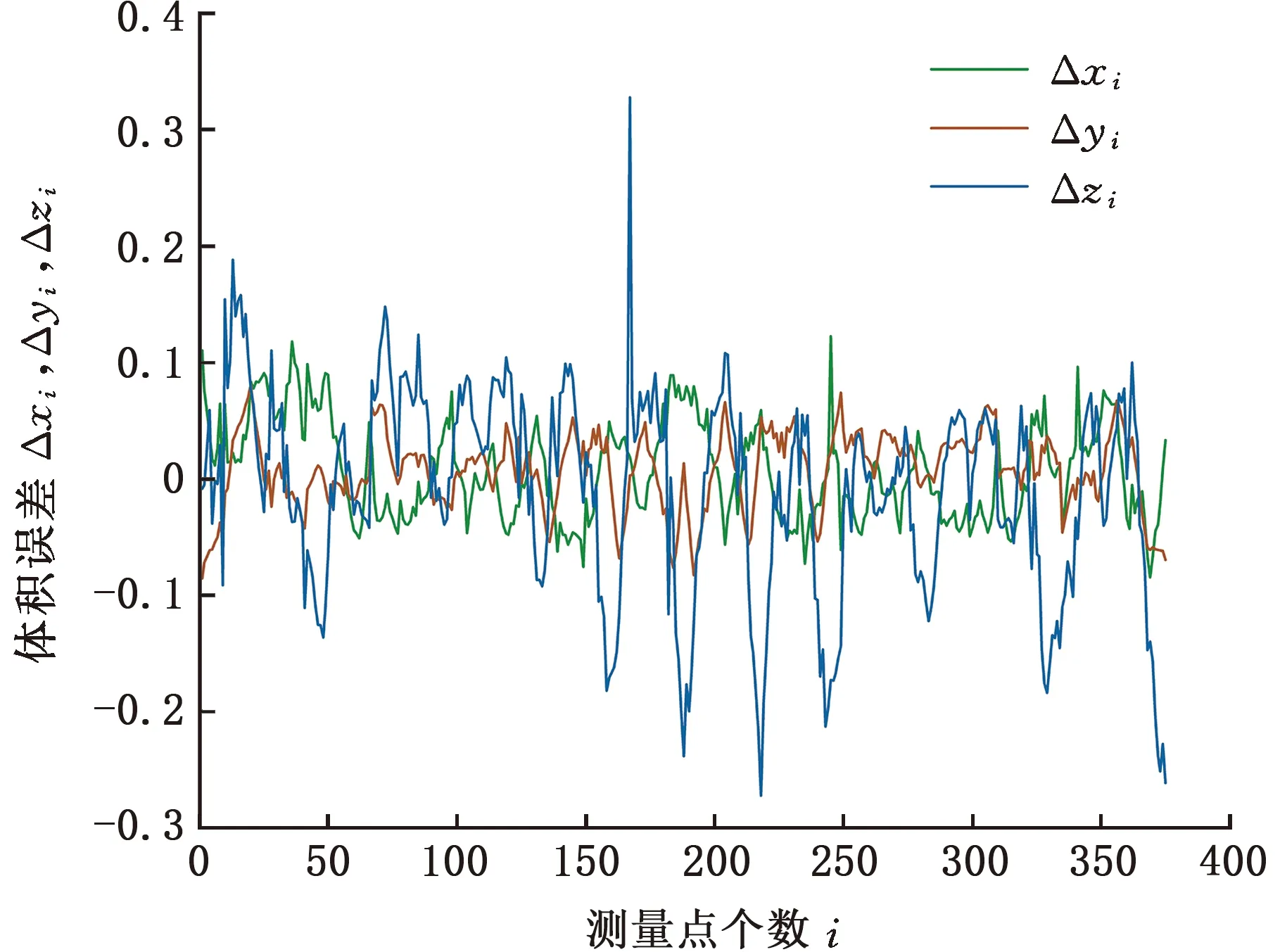
图5 三坐标测量机体积误差Fig.5 Volume error of CMM

2.2.3CMM几何误差的求解

将2.2.2节中测量的体积误差及待测点坐标代入CMM体积误差与几何误差之间的关系式(式(4)～式(6))，建立目标方程组，利用弹性网络算法求解，获得除εz(x)、εx(z)、εy(z)、εz(z)之外的17项几何误差。将求出的部分几何误差代入式(19)～式(20)，利用QR分解求解出εz(x)、εx(z)、εy(z)、εz(z)4项几何误差，最终获得CMM的21项几何误差。不同惩罚因子对应的最小二乘均方误差如图6所示。求解出的垂直度误差分别为αxy=3.06 μrad，αxz=-0.75 μrad，αyz=-3.57 μrad，其余18项x、y、z轴位移误差及旋转误差如图7所示。

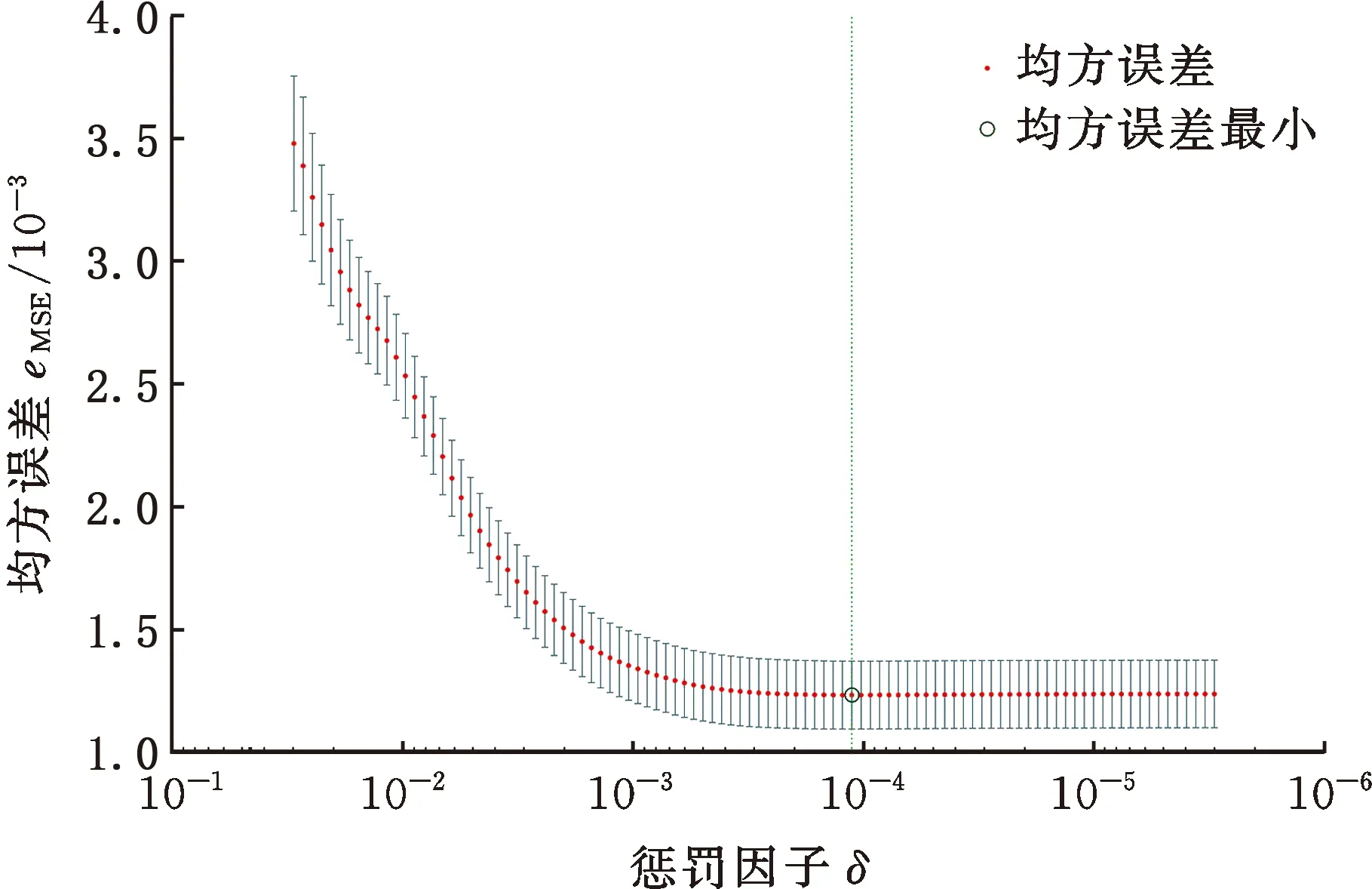
图6 均方误差与惩罚因子对应关系Fig.6 Correspondence between mean square errorand penalty factor

3 结论

(1)本文基于激光追踪仪多站位测量技术实现了大型CMM空间规划点体积误差的高精度测量；

(2)提出了基于弹性网络算法求解三坐标测量机几何误差的方法，解决了CMM准刚体模型求解存在多重共线的难题；

(3)实验测量了大型CMM的空间待测点体积误差，表明本文提出的方法为大型CMM在现有硬件基础上的精度提升提供了新思路。

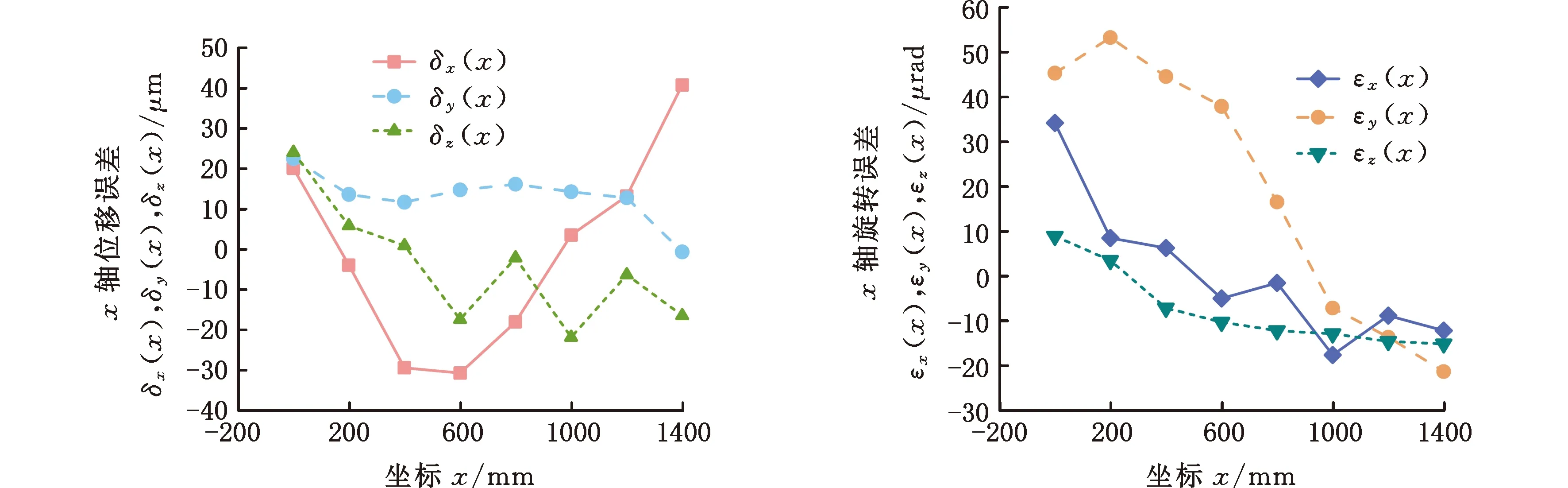
(a)x轴位移误差 (b)x轴旋转误差

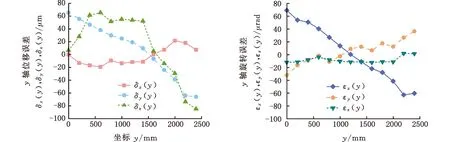
(c)y轴位移误差 (d)y轴旋转误差

(e)z轴位移误差 (f)z轴旋转误差图7 x、y、z轴位移误差及旋转误差Fig.7 x, y, z axis displacement errors and rotation errors