基于电极位移的点焊飞溅量化评价与自适应控制研究

李 欢 吕天乐 夏裕俊 李永兵

上海交通大学上海市复杂薄板结构数字化制造重点实验室，上海，200240

0 引言

电阻点焊技术因其生产效率高、成本低等优势，一直以来都是薄板结构尤其是汽车车身的主要连接工艺[1]。据统计，通常一台轿车车身上有4000～6000个焊点，占到整车焊装总量的90%，焊点质量非常影响车身结构的安全性和可靠性[2]。然而，大规模生产中工况的波动会降低焊接工艺的有效性，造成许多焊接缺陷，飞溅就是较为常见且严重的一种。飞溅会导致熔核尺寸减小，焊点质量不合格[3]，因此，对飞溅进行管控十分必要。在实际生产过程中，存在各种异常情况，其中边距工况是最常见的异常情况，它的存在严重影响焊接质量[4]。

研究人员发现，飞溅现象的发生总是伴随着过程信号的突变。WEN等[5]对不锈钢点焊过程中的动态电阻信号进行了研究，测试了不同焊接工艺条件(边距工况、装配不良、轴向偏差等)的影响，结果表明动态电阻信号在飞溅发生时存在瞬时陡降，可以用来判断飞溅是否发生。FARSON等[6]通过监测电极位移信号，发现其突变量与压痕深度显著相关。JI等[7]对铝合金点焊的电极力和电极位移信号进行了研究，指出在发生飞溅时，电极力和电极位移信号均会发生明显的下降，此现象反映了熔融液态金属的飞溅。ZHANG等[8]将电极位移曲线转化为二值矩阵，通过与概率神经网络相结合，对焊点质量进行检测，在小样本中可快速准确地识别飞溅焊点。LUO等[9]对声信号进行了研究，提出声发射信号的振幅可以反映飞溅程度。可以看出，通过过程信号识别飞溅的研究已经比较成熟了。

在飞溅管控方面，传统方法主要采用人工离线调整焊接参数。较先进的控制方法是采集实时信号并进行反馈控制[10]。HWANG等[11]对比了恒流焊接工艺和多脉冲焊接工艺对 Al-Si 镀层热成形钢点焊的影响，发现多脉冲焊接工艺可以有效抑制飞溅，获得高质量焊点，但是多脉冲焊接工艺会显著增加焊接时间。SHIM等[12]对比了恒功率焊接和恒流焊接对飞溅的影响，发现在相同的工况下，恒功率焊接有助于获得更高的热输入，减少由于热输入过大导致的前期飞溅，但恒功率焊接缺乏参数设置标准，需要根据不同工况手动调整焊接功率。此外，MIKNO等[13]对比了飞溅时电极力和电极位移的变化，发现由于电极力信号的高动态性，跟踪电极力信号能更有效地控制焊接过程。然而，ZHOU等[14]指出，跟踪过程信号是通过增大焊接电流来减弱异常工况影响的，在某些异常工况下，此方法会增加飞溅的可能，并不能保证焊接质量。可以看出，以上飞溅管控策略在特定工况下效果良好，但当工况变化时，有可能失效。SHEN等[15]提出了一种电流短时调幅策略，以应对复杂的焊接工况，实验结果表明该策略具有较强的鲁棒性，但是，在初始电流较大的情况下，该策略会导致调幅次数增多、补时时间变长，显著增加焊接时间。

本文提出了一种基于量化统计的电流调幅自适应控制策略，以解决电流短时调幅策略中调幅次数多、补时时间长的问题。文章介绍了实验装置、焊接工况和测量方法，进行了飞溅特征量的选择，提出了一种基于量化统计的电流调幅自适应控制策略，具体分析了量化统计调幅策略的各个参数，并通过实验对新方法与原方法进行了对比和验证。

1 实验设备与方案

1.1 设备

本文使用的电阻点焊实验平台包括FANUC R2000iB型六轴电阻点焊机器人、CENTERLINE C型伺服焊枪、MEDAR 6000s 型中频直流(MFDC)焊接控制器(逆变频率1 kHz)以及电流、电压、电极力和位移等过程信号的测量传感器，如图1所示。传感器的所有输出信号由数据采集设备以500 kSPS的采样频率进行采集，然后显示在计算机上。由于传感器安装位置远离电极，故信号采集不会干扰焊接过程。焊接过程使用端面直径6 mm的电极帽，冷却水流量为11.3 L/min。

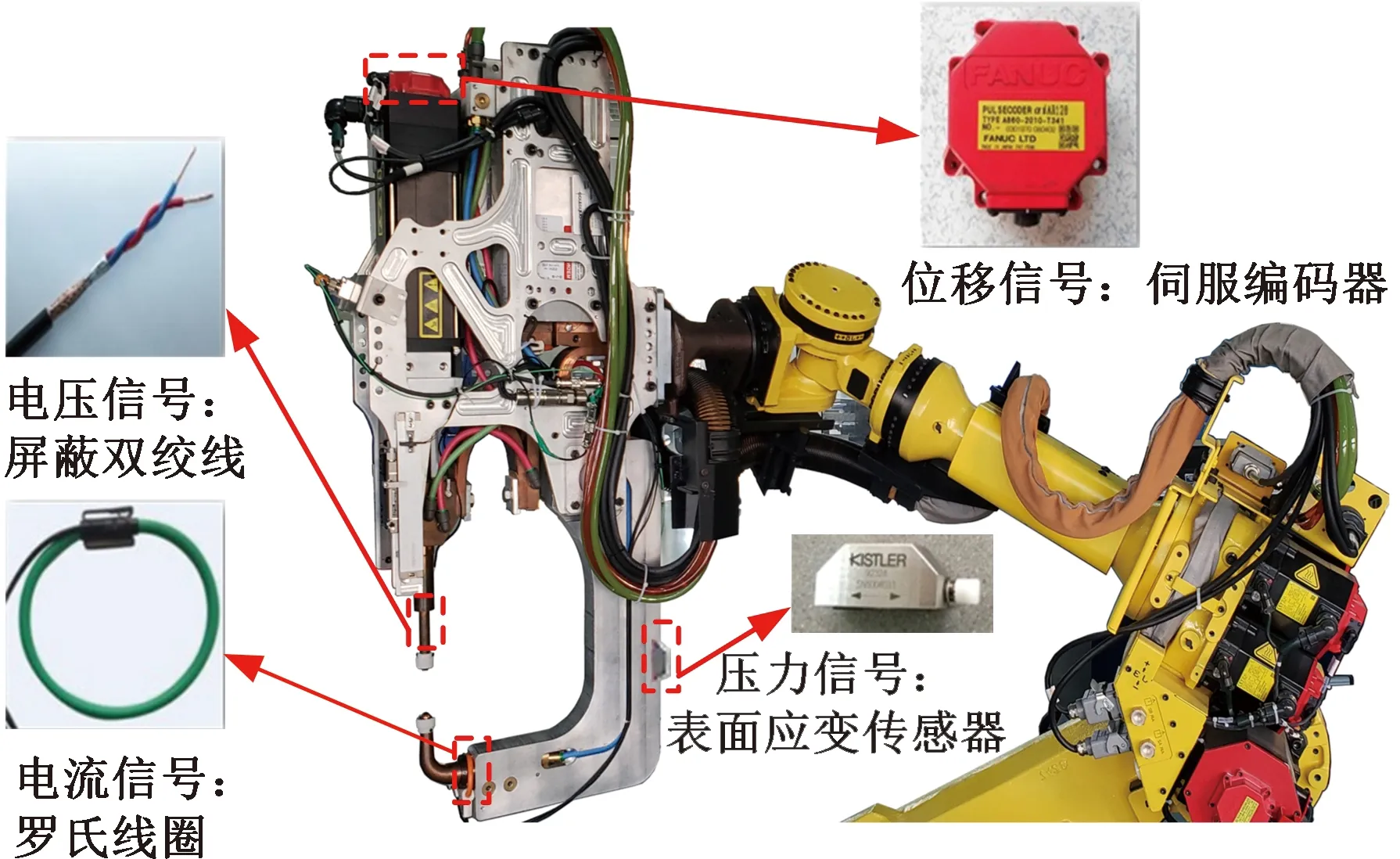
图1 C型伺服焊枪及传感器示意图Fig.1 Schematic diagram of the C-type servo gunequipped with multiple sensors

在电阻点焊工艺中，两个或两个以上的板材被一对电极以电极力F(由安装在下电极臂上的KISTLER表面应变传感器测量，精度为2%)压住，在电压U(由接在上下电极上的屏蔽双绞线测得)的作用下，焊接电流I(由挂在下电极臂上的一个 MEATROL Rogowski 线圈测量，精度为0.5%)通过板材产生焦耳热，在板间形成熔核。根据欧姆定律，动态电阻R计算如下：

(1)

其中，Rg为伺服焊枪的基值电阻，即两电极之间不放置板材时的电阻。此外，由安装在线性导轨上的伺服编码器HEIDENHAIN(标称分辨率0.5 μm)测量移动电极位移Sm。

根据文献[16]，固定电极(上电极)位移Sf与F成正比，则两电极之间的相对位移S计算如下：

(2)

其中，Kg为伺服焊枪固定电极臂的等效刚度系数。根据文献[16]，为了获得Kg，需要将焊枪闭合、两电极在不同电极力下接触，此时移动电极位移Sm可以近似替代固定电极位移Sf，从而获得固定电极位移Sf和电极力F关系，通过曲线拟合即可测定等效刚度系数Kg，本实验中测定Kg为 4.54 kN/mm。

1.2 焊接工况及材料

图2为实验所用试样尺寸及边距工况示意图。试样尺寸均为138 mm×38 mm。边距工况表示焊点靠近较长侧的边缘，本研究中设置边缘距离为3 mm。

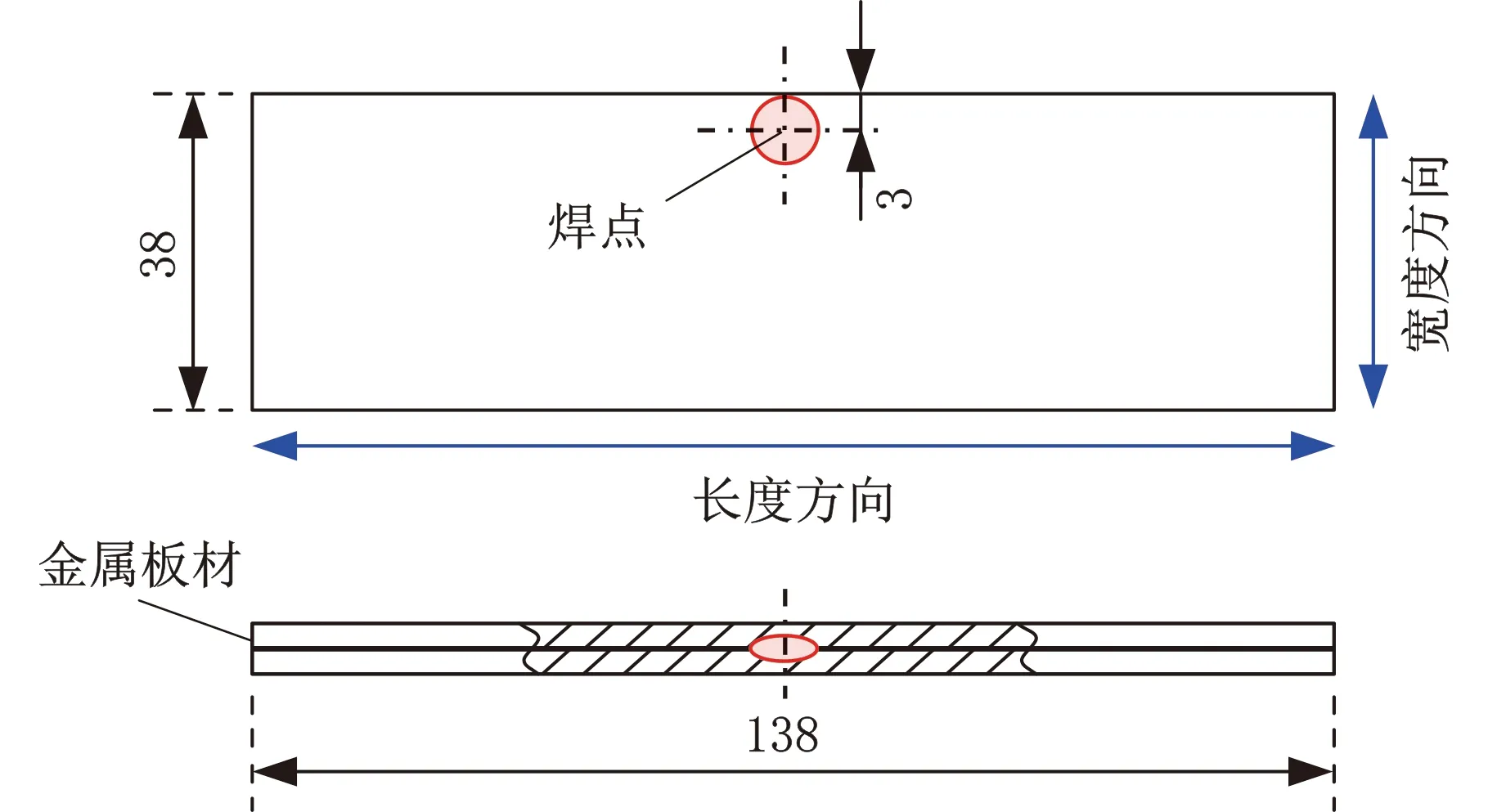
图2 试样尺寸及边距工况示意图Fig.2 Specimen dimensions and Edge proximitycondition diagram

由于车身连接中存在不同的板材组合，为了提高管控策略的实用性，实验选取了两种不同厚度、不同强度的板材：BUSD和DP590，它们的化学成分及力学性能如表1、表2所示。

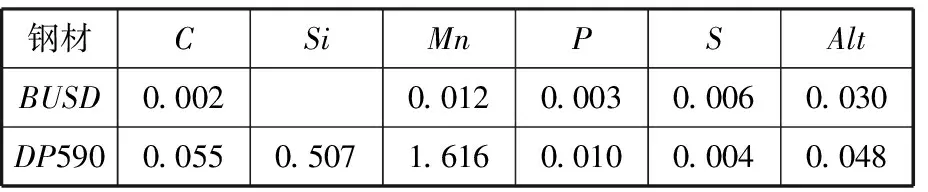
表1 BUSD和DP590的化学成分(质量分数)

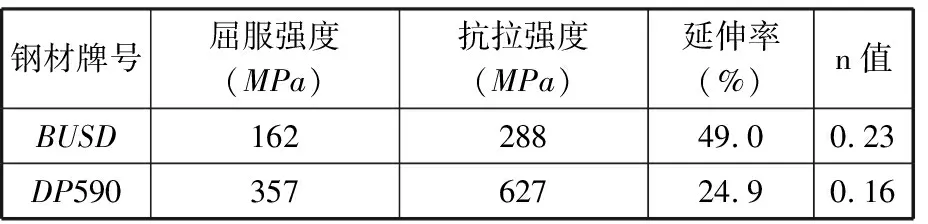
表2 BUSD和DP590的力学性能

实验设计了2种方案，表3给出了边距工况下这2种方案的焊接参数。

1.3 飞溅金属质量的测量

飞溅金属质量是衡量飞溅程度最直接、最有效的特征量，实验中通过离线剥离的方式来确定各个焊点的飞溅程度。根据之前的研究[17]，飞溅金属量测量过程如下：

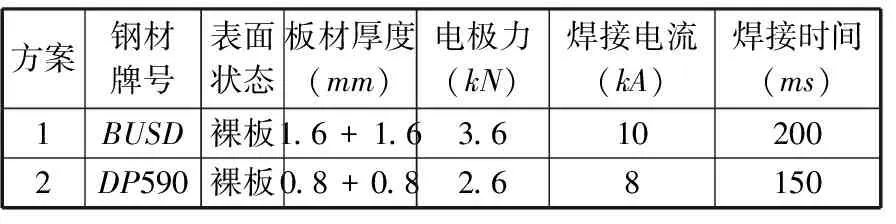
表3 由两种板材组成的焊接方案

(1)使用精度为 1 mg的数字天平称量焊接前的板材质量m0；

(2)使用数字天平称量焊后工件质量，记为m1。因此发生飞溅时飞出液态金属的质量Δme可计算如下：

Δme=m0-m1

(3)

(3)剥离工件，剔除残留的飞溅金属，再次使用数字天平称量板材质量m2。因此飞溅金属总质量Δm可计算如下：

Δm=m0-m2

(4)

1.4 熔核尺寸的测量

异常焊接条件会引起熔核不对称生长，因此，如图2所示，需要测量两个正交平面上的熔核直径和熔核厚度，并采用平均熔核直径Dn表征熔核尺寸：

(5)

其中，DL和DW分别代表长度和宽度方向的熔核直径，平均熔核厚度Hn计算方法同理。为保证测量精度，都进行了5次重复实验。压痕深度HI的计算公式如下：

HI=2h-Hn

(6)

其中，h为板材厚度。

2 飞溅量化评价

图3所示为边距工况下以7kA电流焊接DP590板材时的过程信号，可以看出，飞溅时刻texp在145 ms左右，此时电阻信号突变量为ΔR，位移信号突变量为ΔS，与文献[5-6]的研究结果一致，说明电阻信号和电极位移信号均适用于识别飞溅。

图4a、图4b为边距工况下以8kA电流焊接DP590板材发生飞溅时电阻信号突变量ΔR与飞出金属的质量Δme和飞溅金属的总质量Δm的关系图。图4c、图4d为同种工况下发生飞溅时位移信号突变量ΔS与飞出金属的质量Δme和飞溅金属的总质量Δm的关系图。由图4a、图4b可以看出，ΔR与Δme、ΔR与Δm之间均没有明确的相关性，即不能通过电阻信号突变量ΔR评估飞溅程度。从图4c、图4d可以看出，ΔS与Δme之间也没有明确的相关性，而ΔS与Δm之间存在线性关系，拟合的斜率为0.207，线性相关系数R2为0.955，均方根误差(RMSE)为5.69，线性度较好，这一结果与XIA等[17]的研究结果一致，说明位移信号突变量ΔS可作为飞溅量化评价的重要指标。

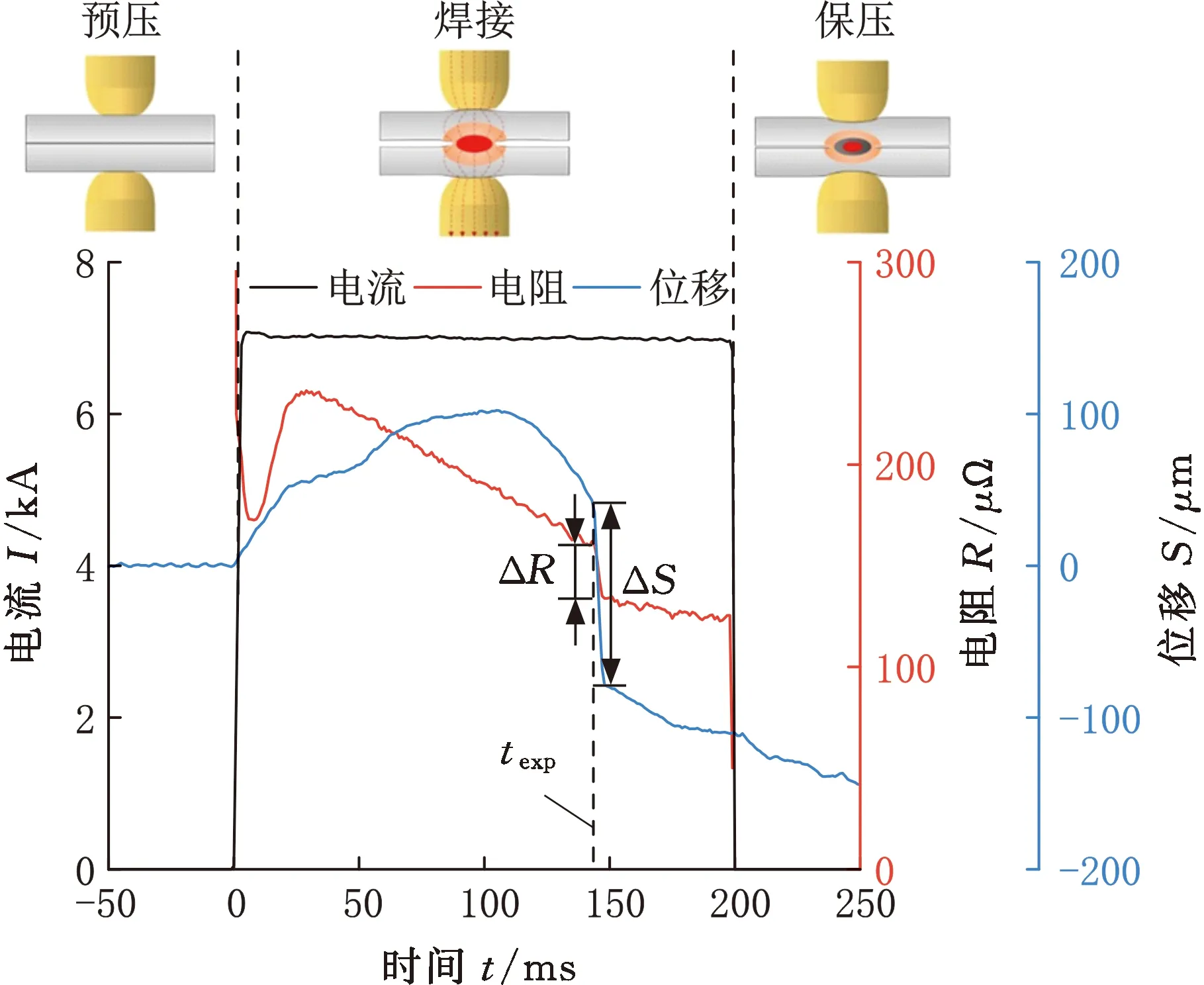
图3 恒流模式下的电阻和位移信号 Fig.3 Resistance and displacement signals ofconstant current

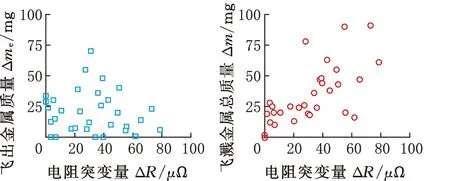
(a)ΔR与Δme的散点图 (b)ΔR与Δm的散点图

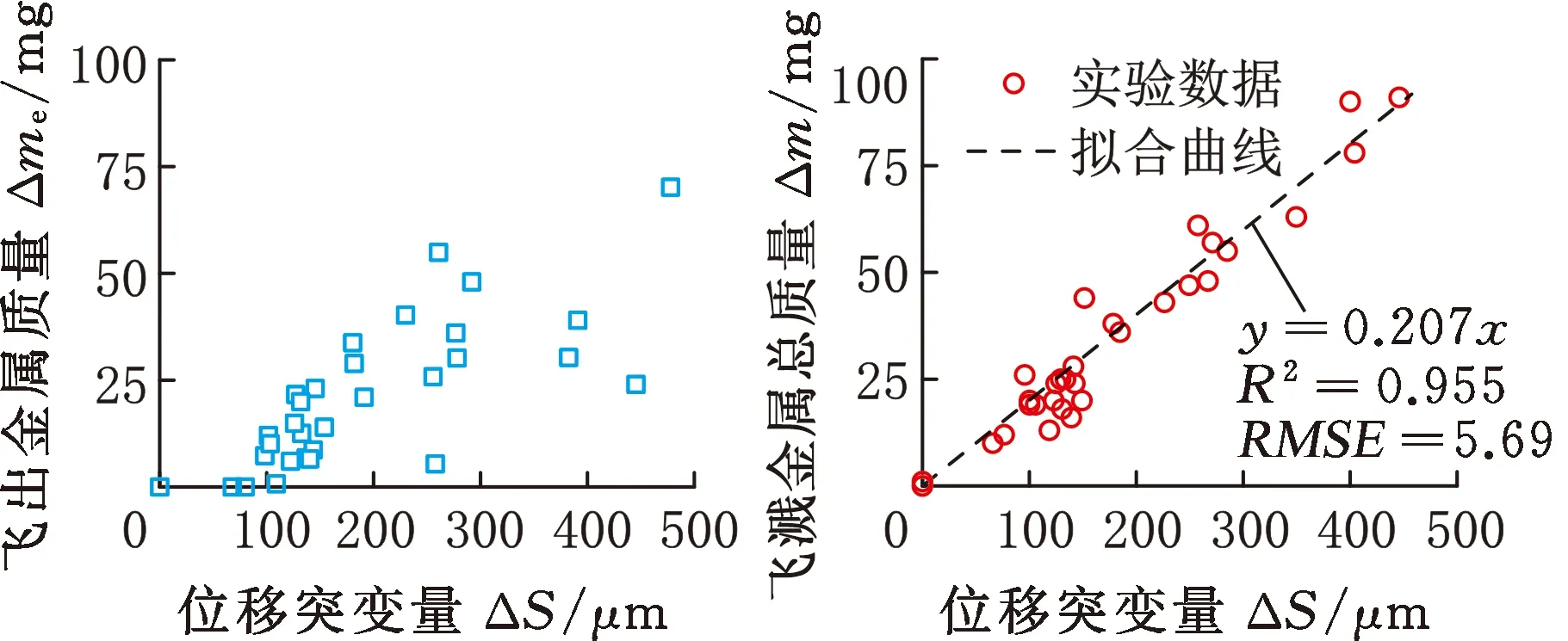
(c)ΔS与Δme的散点图 (d)ΔS与Δm的散点图图4 过程信号突变量与飞溅金属质量的散点图Fig.4 Scatter diagram of process signal suddenchange and expulsion metal quality

另外，通过金相观察实验，分析了飞溅发生前后的熔核尺寸，结果如图5所示。由图5a可以看出，飞溅发生在78 ms，对应的位移信号突变量ΔS为306 μm。图5b为飞溅前1 ms(77 ms时)和飞溅后1 ms(79 ms时)的熔核形貌，可以看出，在电极力的作用下发生了飞溅，熔核内部出现空腔，飞溅发生前后熔核直径基本不变，熔核厚度从2.6 mm减小到2.28 mm，减小了320 μm，与位移信号突变量ΔS近似相等，再次验证了位移信号突变量ΔS可作为飞溅特征量。

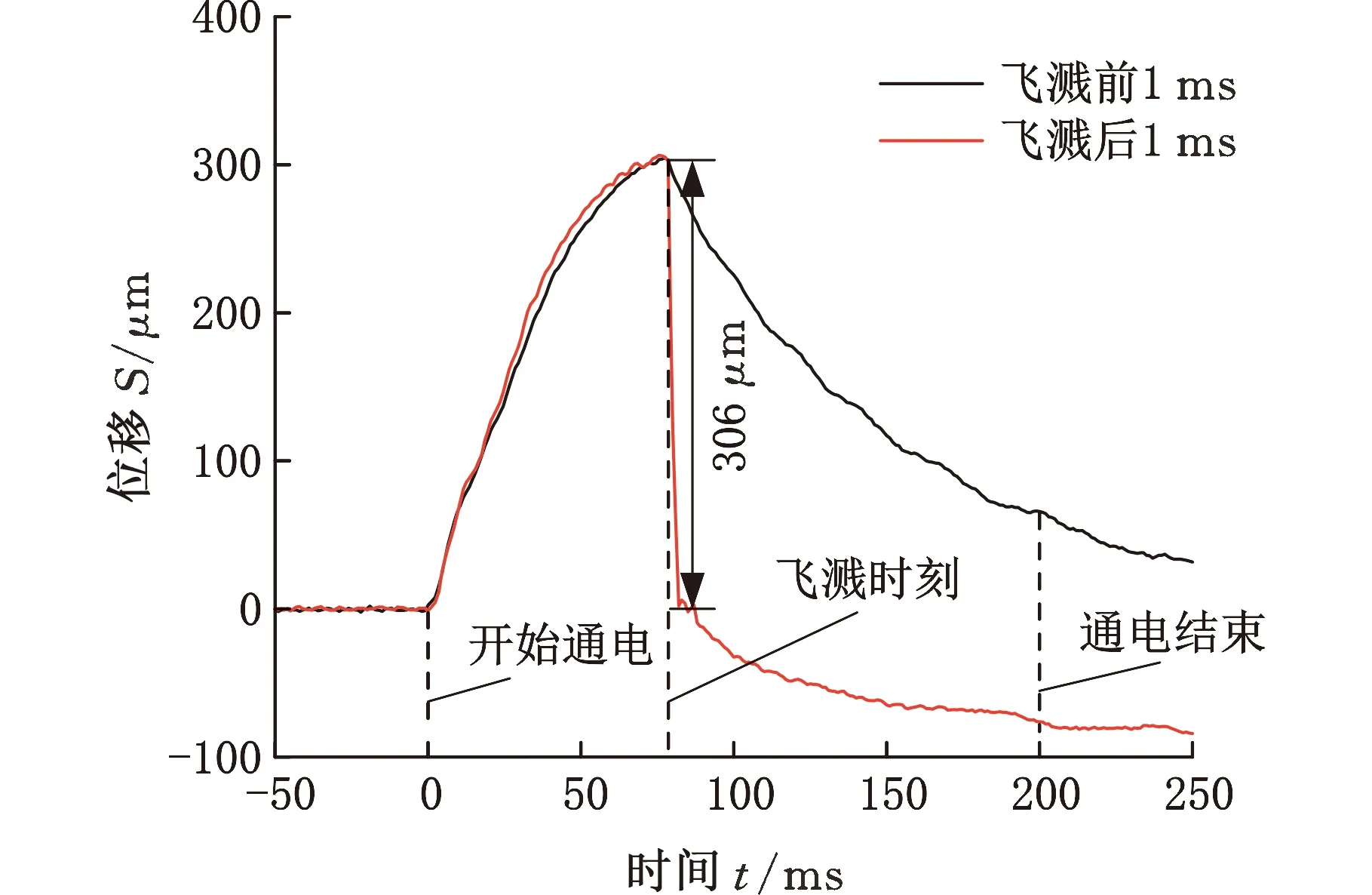
(a)飞溅前后位移曲线对比

(b)熔核形貌(mm)图5 飞溅发生前后的位移信号及熔核形貌Fig.5 Displacement signal and metallographic diagrambefore and after expulsion

3 飞溅在线管控策略

因为通过电极位移信号可以有效地在线识别飞溅和量化飞溅程度，故本文采用位移信号突变量作为飞溅特征量进行统计分析，进而开展基于量化评价的电流调幅，实现飞溅的自适应控制，以适应快节拍复杂多变的焊接工况。

基于量化评价的调幅策略包含飞溅程度评估、自适应电流调幅、恒功率能量补充三个部分。飞溅程度评估通过电极位移信号识别飞溅，计算飞溅特征量ΔS，统计出一定周期内的平均飞溅时刻tavg和平均飞溅特征量ΔSavg。自适应电流调幅即根据统计结果对参数进行自适应选择，进而实现不同工况下的适应性。恒功率能量补充即在电流调幅后，通过补充一定的焊接时长来弥补由于电流调幅导致的热输入下降，从而保证熔核质量。

3.1 飞溅程度评估

图6所示为边距工况下以7kA电流焊接DP590时的飞溅程度评估情况。由图6b可以看出，飞溅特征量ΔS在均值ΔSavg附近波动，分布比较集中，故可认为同一工况下，飞溅特征量ΔS基本一致。图6c所示为飞溅时刻texp的统计图，计算分析texp的分布可得，均值tavg为91.7，方差σ2为7.01，峰度系数为-0.59，偏度系数为0.0023。由于峰度系数与偏度系数的绝对值均小于1，故可认为飞溅时刻texp呈正态分布，即texp～N(91.7, 7.01)。最终将统计得到的正态分布参数及平均飞溅特征量ΔSavg记录下来。

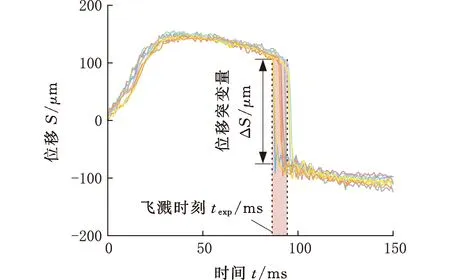
(a)位移信号曲线

(b)ΔS统计图 (c)texp统计图图6 边距工况下DP590板材的飞溅统计示意图Fig.6 Expulsion statistics diagram of DP590 sheetunder edge proximity condition

3.2 自适应电流调幅

异常工况下焊接时，短时间内热输入过大导致熔核增长过快，当熔核突破塑性环时就会发生飞溅。其中，短时间内热输入越大，飞溅程度越严重，位移信号突变量越大。电流调幅的思想是在飞溅前降低电流以减少热输入，从而抑制飞溅，减小位移信号突变量。在调幅过程中，存在3个参数，即调幅时刻t0，调幅时长td，调幅系数α，其中t0确定调幅的时刻，td与α确定调幅的力度。如图7所示，调幅时刻t0为0，根据电流调幅的思想，下次焊接时，区间[tavg-td-t0,tavg-t0]内的电流为初始电流的α倍。

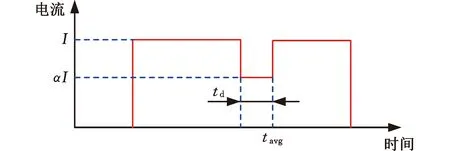
图7 电流调幅示意图Fig.7 Schematic diagram of current amplitude modulation

自适应电流调幅即根据飞溅程度和飞溅概率，采用模糊控制算法确定调幅参数。

(1)调幅时刻t0。由图6c统计结果可知，飞溅时刻texp均落在区间[tavg-3σ，tavg+3σ]内，且根据正态分布的性质可知，飞溅时刻texp落在区间[tavg-3σ，tavg+3σ]内的概率为99.7%，所以若飞溅时刻落在区间[tavg-3σ，tavg+3σ]内，则认为texp～N(tavg,σ2)。如果飞溅时刻texp服从N(tavg,σ2)时texp不在区间[tavg-td-t0,tavg-t0]内，可能是由于随机波动导致飞溅时刻提前，则飞溅时刻t0增加σ。t0初始值为0且最大不超过3σ。

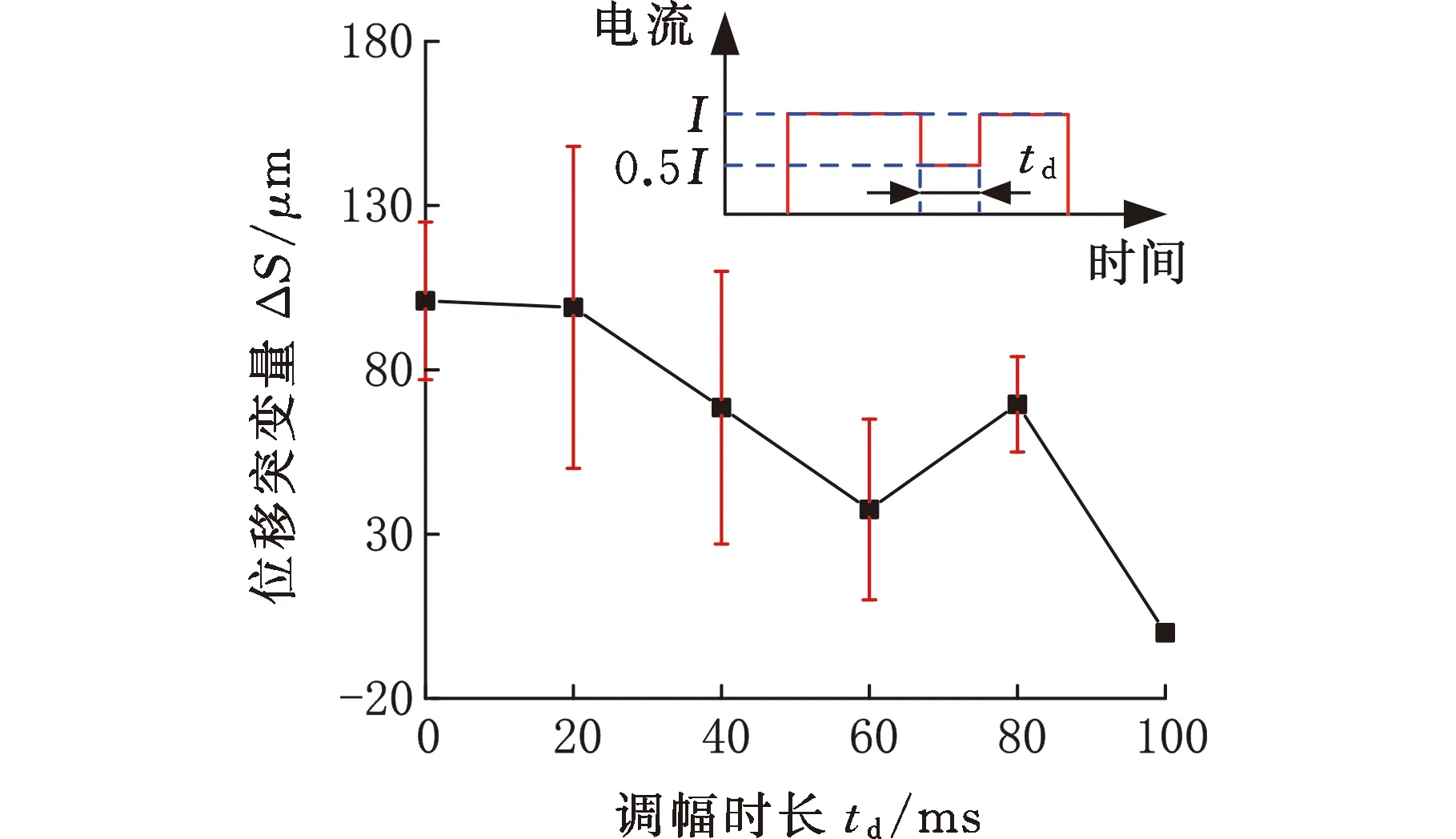
(a)td与ΔS的关系图

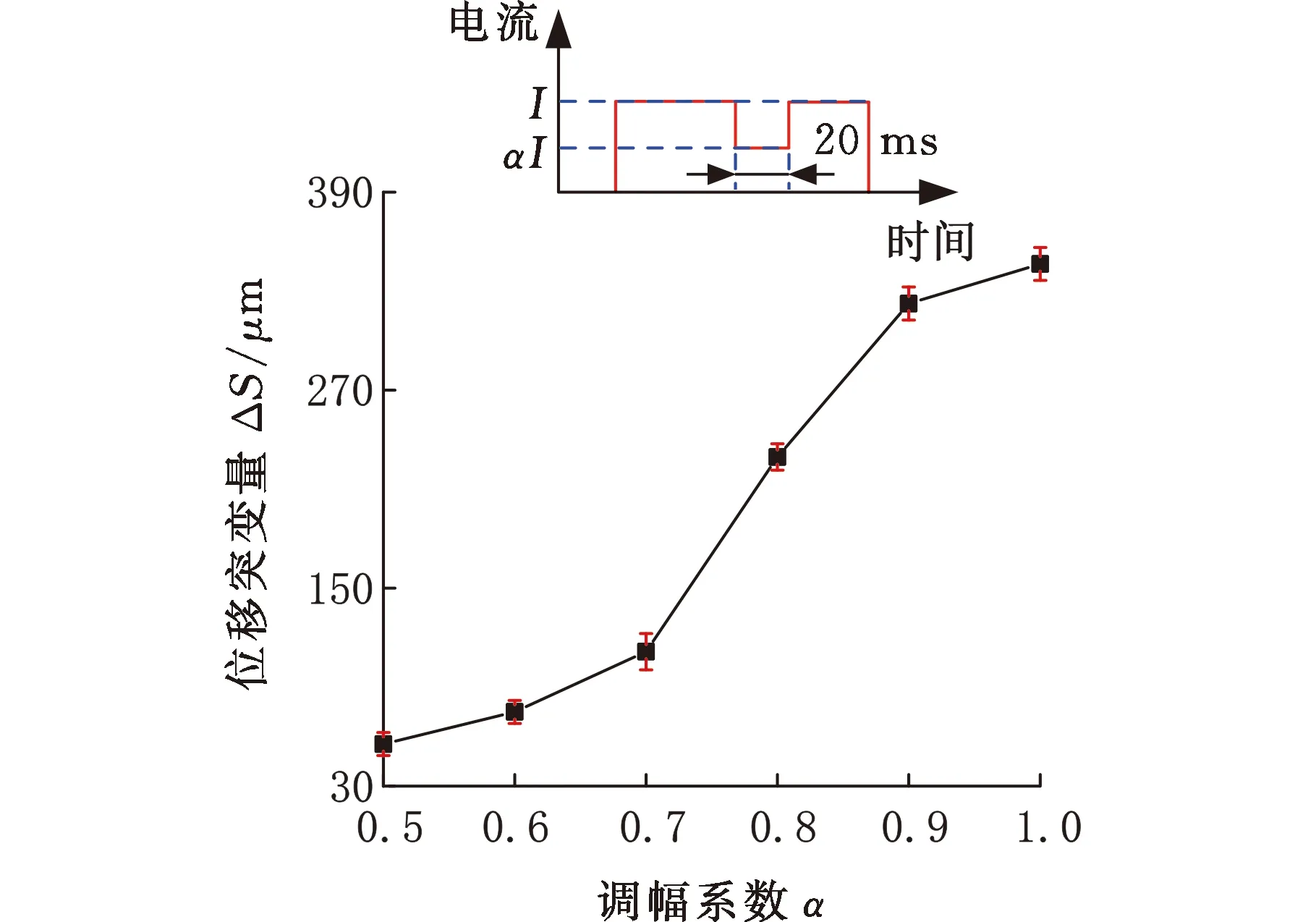
(b)α与ΔS的关系图图8 调幅时长与调幅系数对飞溅量的影响Fig.8 Effects of amplitude modulation duration andamplitude modulation coefficient on expulsion

(2)调幅系数α与调幅时长td。为了探究调幅系数α和调幅时长td对飞溅抑制的影响，以8kA电流对DP590板材进行了焊接，调幅时刻t0为0。如图8a所示，调幅系数α为0.5，不断增大调幅时长td时，飞溅特征量ΔS总体趋势下降，但波动较大，下降不明显。图8b中，调幅时长td为20 ms，随着调幅系数α的不断减小，飞溅特征量ΔS不断减少，且波动较小。实验结果说明调幅系数α对ΔS的影响较大，调幅时长td对ΔS的影响较小。因此将调幅系数α作为主要研究对象。

根据SHEN等[15]的研究，飞溅的发生是由于熔核增长过快，熔核尺寸突破塑性环造成的。图9a为边距工况下以8kA初始电流对DP590板材进行焊接的电流示意图，实验采用0.35～0.95的调幅系数α，调幅时刻t0为0，调幅时长td为20 ms。对调幅后的焊点进行金相分析，测量其熔核直径Dn与塑性环直径DC，如图9b所示。由图9c可以看出，随着调幅系数α的增大，塑性环与熔核直径均不断变大，其中塑性环尺寸增加比较均匀，而熔核在小电流下增长缓慢，电流变大时急剧增长，说明熔核对电流的敏感度比塑性环大。小电流时，熔核增长速度小于塑性环，电流增大时，由于熔核对电流的敏感度更高，导致熔核增长大于塑性环，因此，当调幅系数α取0.65时，熔核与塑性环之间的尺寸差达到最大值，为0.24 mm。

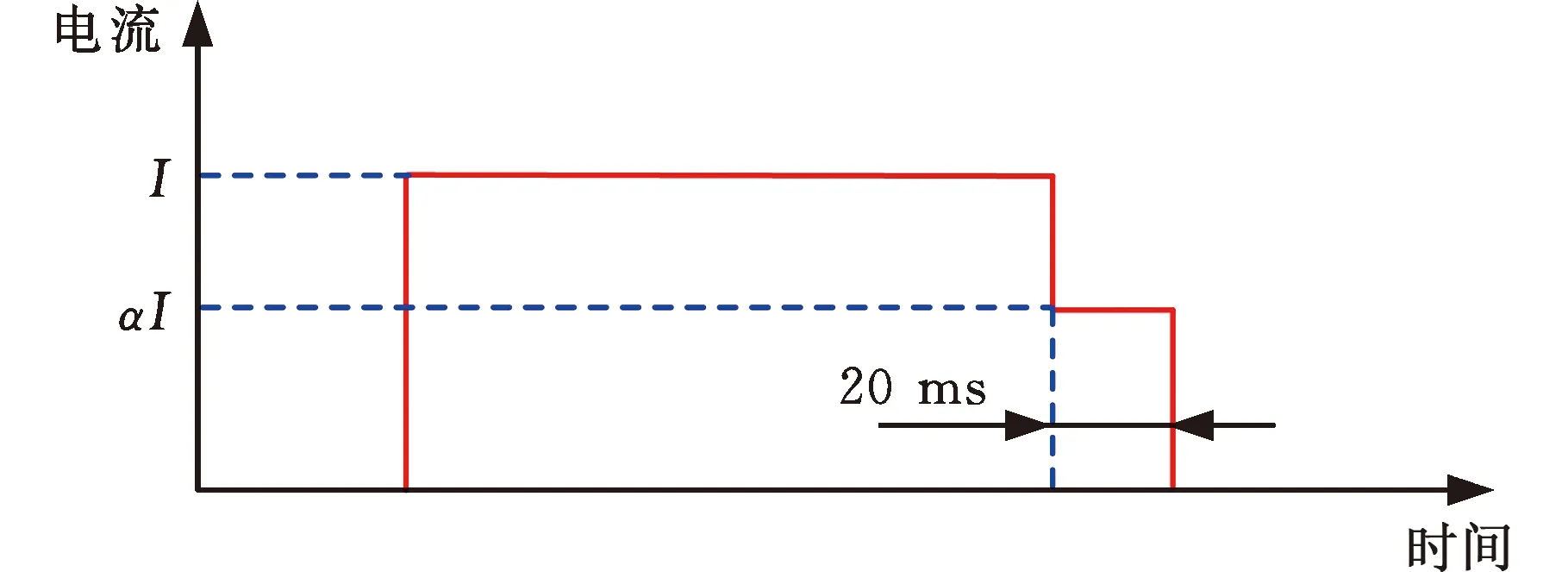
(a)焊接电流示意图

(b)熔核直径Dn及塑性环直径DC测量示意图

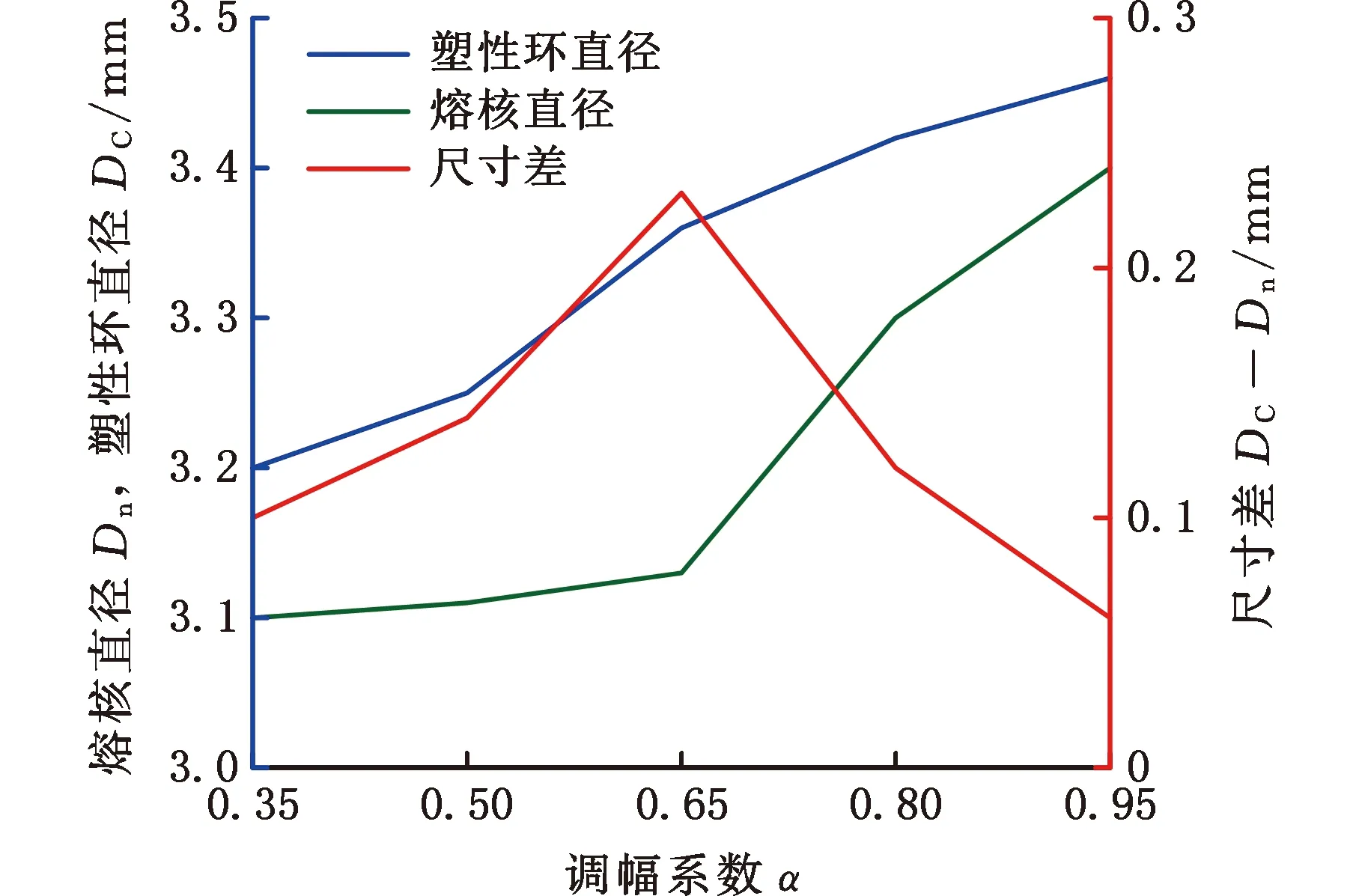
(c)调幅系数与熔核、塑性环尺寸及尺寸差的关系图9 调幅系数与塑性环及熔核尺寸的关系图Fig.9 Relationship schematic diagram of amplitudemodulation coefficient and corona and nugget size

在实际调幅的过程中，为了最大程度地抑制飞溅，需要不断调整调幅系数α，使得塑性环与熔核之间的尺寸差达到最大。为了减少调整次数，提高调幅效率，采用基于飞溅量化评价的控制策略——模糊控制算法——以实现自适应调幅过程。算法输入为飞溅特征量ΔS和飞溅概率p。根据图6b统计结果，以7kA电流焊接(0.8+0.8)mm DP590板材时，平均飞溅特征量ΔSavg为193.5 mm，约为板材总厚度的12%。因此可将飞溅特征量ΔS分为三个等级，ΔS在板材厚度8%～12%范围内为M，大于12%为L，小于8%为S。飞溅概率p分为三个等级，p在0～0.3之间为S，在0.3～0.7之间为M，在0.7～1之间为L。表4所示为模糊控制规则表，其中不同程度的飞溅特征量ΔS和飞溅概率p对应不同的初始调幅系数α。经过电流调幅后，若仍发生飞溅，则α自减0.1，α不小于0.5。

由图8a可以看出，随着调幅时长td不断增大，飞溅特征量ΔS虽波动较大，但总体趋势仍在下降，即调幅时长td对飞溅的影响较小。在调幅的过程中，当α为0.5时仍发生飞溅，可适当增加调幅时长td，直到飞溅完全消除。td初始值为σ，每次增加σ。

3.3 恒功率能量补充

由于短时调幅是通过在飞溅前降低电流强度的方式来管控飞溅的，在相同焊接时长的情况下会导致热输入的下降，为了保证熔核质量，需要增加能量补充机制。由焦耳定律可知：

E=I2Rt

(7)

将式(7)离散化：

(8)

其中，Ii和Ri分别为i时刻的电流和电阻值。

为了保证总体的热输入，需要针对调幅部分进行能量补充。通常，电阻点焊中受控参数为电流、功率等电学相关量。SHEN等[15]研究表明，采用原焊接电流进行能量补充会导致飞溅时刻后移，无法完全消除飞溅。另外，SHIM等[12]指出，恒功率焊接模式可有效抑制飞溅。因此，本文根据前期焊接能量计算平均功率Pavg作为后期补充能量的功率：

(9)

则补时时长ta的计算公式如下：

(10)

其中，ΔE为调幅前后的能量差。不同时刻焊接电流Ia的计算公式如下：

(11)

其中,Ri-1为前一毫秒的电阻值。

为了更直观地解释电流调幅和能量补充的过程，图10展示了参数的具体选择过程，图10a为初始电流波形。首先根据电极位移信号识别飞溅时刻texp，计算飞溅特征量ΔS，对飞溅量进行统计，计算平均飞溅时刻所属正态分布的参数tavg与σ2，平均飞溅特征量ΔSavg及飞溅概率p。图10b为首次调幅电流示意图，初始化调幅参数t0=0，td=σ，同时根据模糊控制规则确定参数α，以α取0.6为例，根据当前参数再次进行焊接，若仍发生飞溅，则将α逐次递减0.1。如果α为0.5时飞溅仍存在，则将调幅时长td增加σ，直至飞溅完全消除。在恒功率补时阶段，根据前期焊接能量计算平均功率Pavg，并根据能量差计算补时时间ta、补时电流Ia，最终电流及功率示意图见图10c。

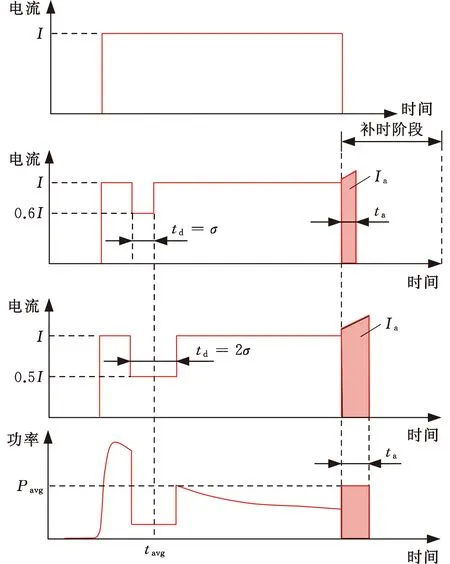
(a)初始电流波形(b)基于量化统计的首次调幅电流(c)最终电流和功率示意图图10 电流及功率调节示意图Fig.10 Schematic diagram of current andpower regulation

图11为基于量化统计的电流控制策略流程图。该策略针对飞溅情况进行调节，且初始统计阶段不进行调幅。在调幅的过程中，通过对位移信号突变量的统计，采用模糊控制算法确定调幅参数，进行前期焊接，以实现自适应电流调幅。同时统计前期焊接的总能量，计算平均功率和补时时间，对后期补时阶段进行恒功率模式焊接，实现自适应能量补充。

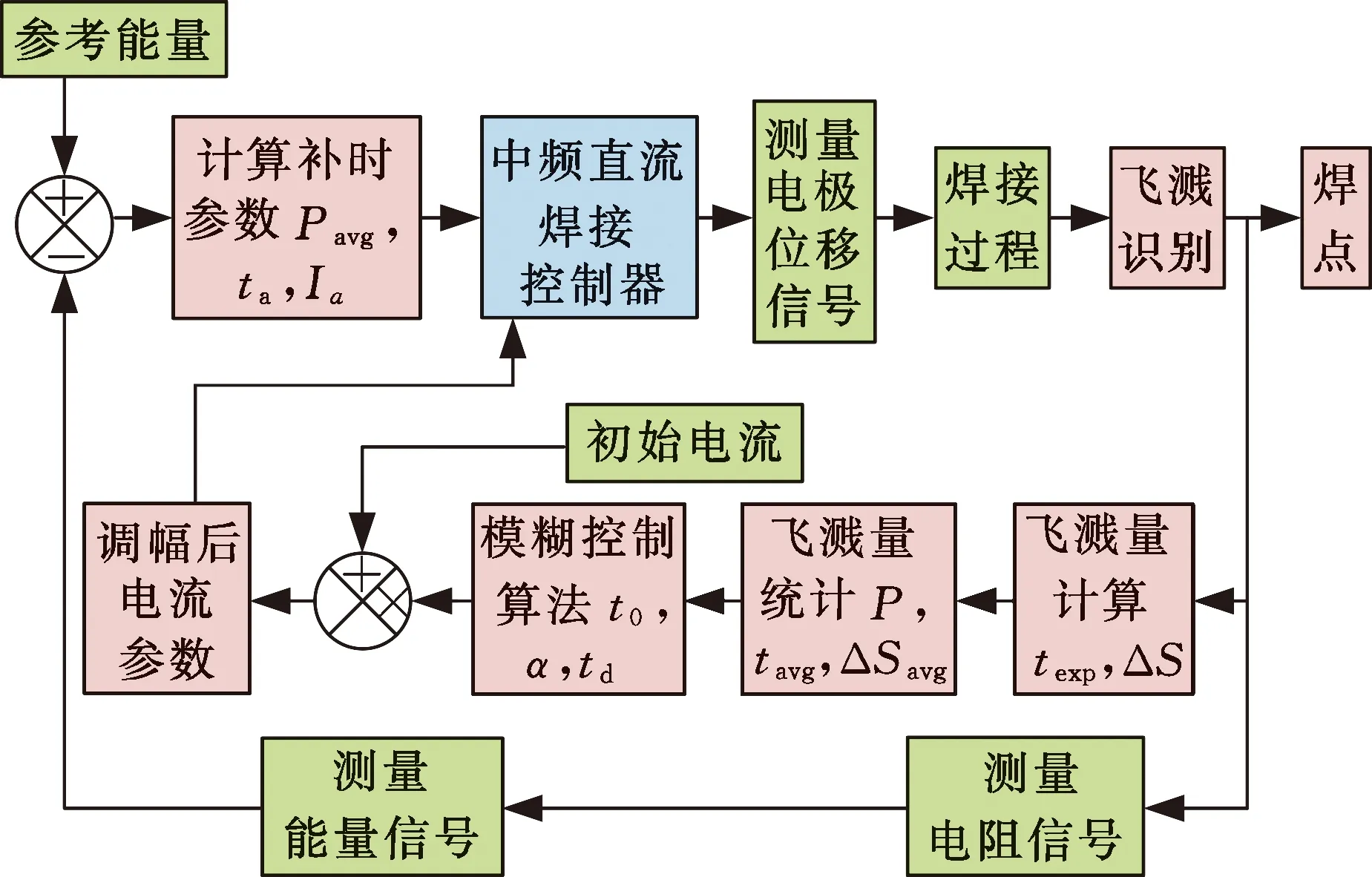
注：初次焊接时不进行调幅和补时(a)基于量化统计的控制方案

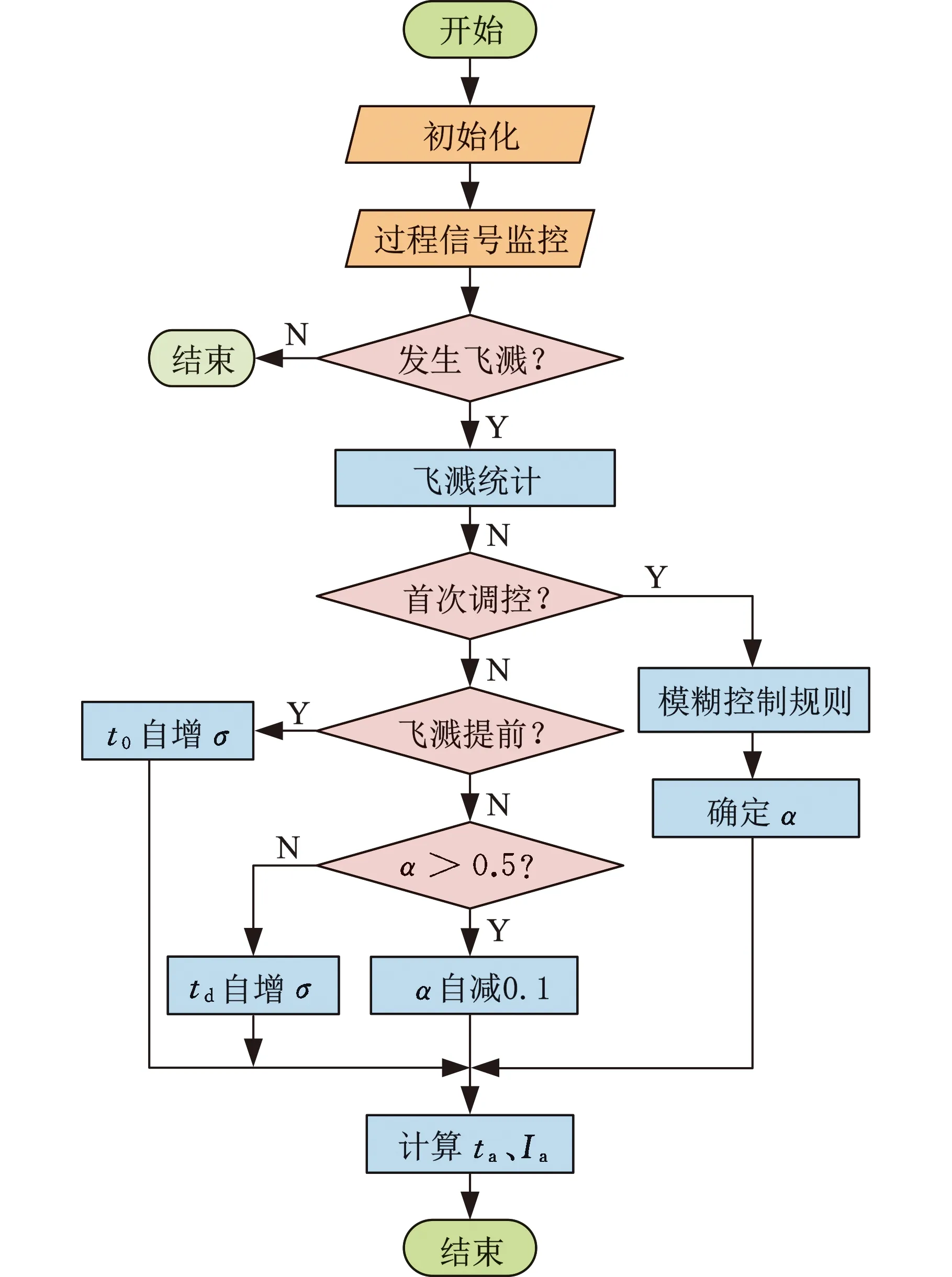
(b)基于量化统计的控制流程图图11 基于量化统计的调幅控制图Fig.11 Control diagram of amplitude modulationstrategy based on quantitative statistics

3.4 策略的可行性验证

图12为边距工况下以8kA初始电流对DP590板材进行焊接的过程信号示意图，可以看出，通过采用基于量化统计的自适应电流调幅策略，最终调幅系数α为0.5，调幅电流4kA。由图12a可以看出，与SHEN等[15]短时电流调幅策略相比，采用量化调幅的恒功率能量补时策略后，补时时长由40 ms减至24 ms，减少了40%。由图12b可以看出，采用恒功率模式的补时能量比短时调幅的补时能量少20 J。

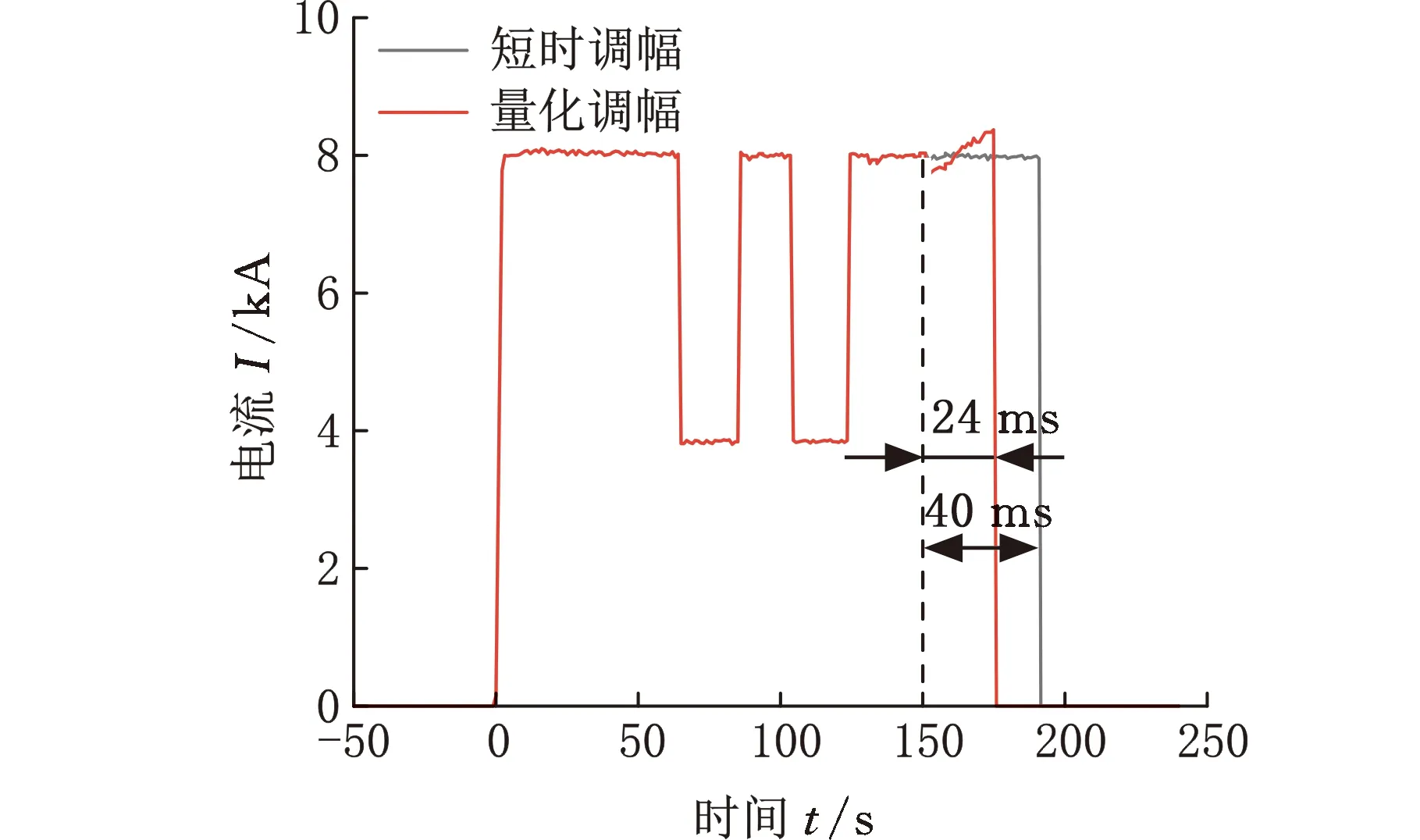
(a)短时调幅与量化调幅的电流对比图

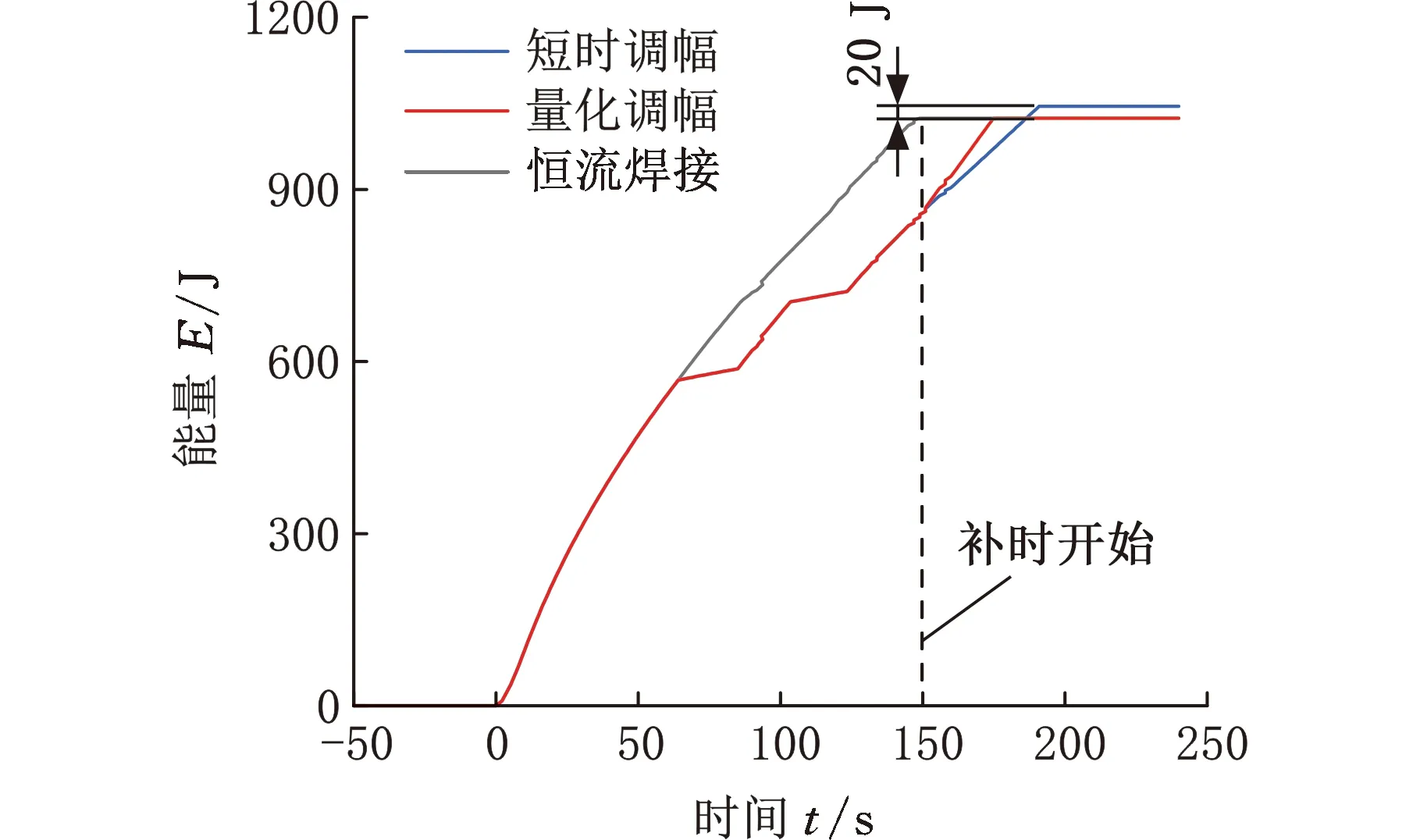
(b)短时调幅与量化调幅的能量对比图图12 短时调幅和量化调幅的电流与能量对比图Fig.12 Current and energy comparison diagram of shorttime amplitude modulation and quantitativeamplitude modulation

为了保证量化统计策略下的焊接质量，对比了边距工况下恒流模式与基于量化统计的调幅策略在两种板材下的结果。

表5所示为2种方案下飞溅特征量ΔS、平均熔核直径Dn、平均压痕深度HI的统计结果，表中“量化”表示基于量化统计的调幅策略，“恒流”表示边距工况下恒流模式。可以看出，相比于恒流焊接，基于量化统计的调幅策略均有效抑制了飞溅，同时平均熔核直径增加0.67 mm，平均压痕深度减少0.24 mm。量化调幅通过在飞溅前降低电流，使得熔核与塑性环的尺寸差达到最大，从而消除飞溅，同时根据焊接功率进行补时，保证焊接质量。实验结果表明，采用量化调幅恒功率策略的补时能量虽然比短时调幅恒流策略的补时能量少20 J，但仍能有效保证焊接质量。

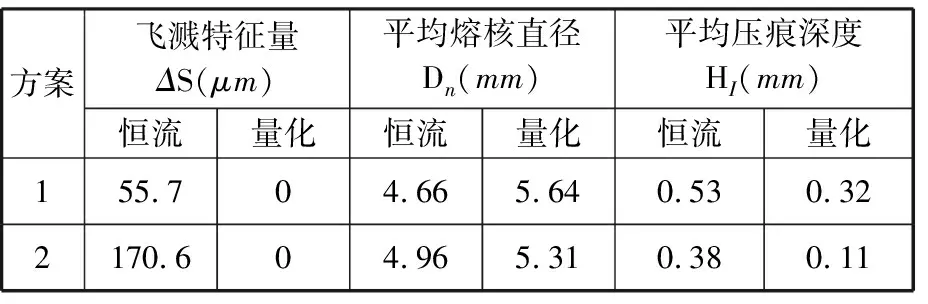
表5 边距工况下2种方案的控制结果

另外通过实验对比了边距工况下短时电流调幅策略与基于量化统计的调幅策略在不同板材下的调整情况，结果如表6所示，表中“量化”表示基于量化统计的调幅策略，“短时”表示边距工况下短时电流调幅策略。可以看出，基于量化统计的调幅策略由于采用模糊控制的自适应方法，相比于短时电流调幅可以更快速地确定调幅系数，从而有效缩短调幅时间，减小调幅次数。同时由于能量补充时采用恒功率策略，在抑制飞溅的同时将补时时长减少了75%，有效提高了焊接效率。

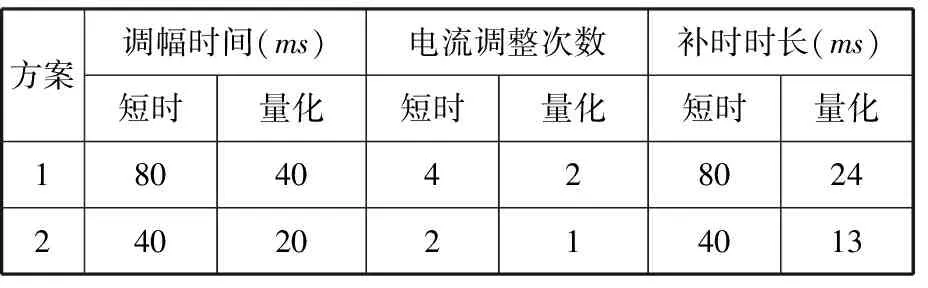
表6 边距工况下2种方案的最终调整时间

4 结论

本文提出一种基于电极位移信号的飞溅量化自适应控制策略来抑制异常工况下不同板材的飞溅情况。通过对BUSD和DP590两种板材进行实验和数据分析可以得出以下结论：

(1)相比于动态电阻信号，电极位移信号更适用于识别及量化飞溅。飞溅金属总质量与动态电阻信号的突变量无关，仅与电极位移信号的突变量线性相关。飞溅发生前后熔核直径基本不变，熔核厚度的减少量与电极位移信号的突变量基本一致，即电极位移信号突变量可作为飞溅特征量来量化飞溅程度。

(2)提出基于量化统计的电流调幅控制策略，制定了以飞溅特征量和飞溅概率为输入，调幅系数、调幅时长和调幅时刻为输出的模糊控制策略。该方法根据飞溅程度确定调幅参数，提高调幅效率。实验表明，与传统短时电流调幅策略相比，该方法可将调幅次数减少50%。

(3)提出基于恒能量与恒功率补时策略，以调幅前后的能量差为补时总能量，以前期功率为补时功率，实现对焊点能量的补充。补时阶段动态电阻减小，恒功率模式下补时焊接电流增大，从而减少补时时间。实验表明，与传统短时电流调幅策略相比，该方法可将补时时长减少75%左右，有效提高生产效率。