视觉显著区域和主动轮廓结合的图像分割算法

何亚茹，葛洪伟+

1.江南大学 江苏省模式识别与计算机智能工程实验室，江苏 无锡214122

2.江南大学 人工智能与计算机学院，江苏 无锡214122

图像分割是实时图像处理的基础研究内容，作为目标提取、识别和跟踪的预处理操作，分割结果的好坏直接影响后续步骤的判断。图像采集过程中，易受设备及外部环境的影响，获取的图像往往存在灰度分布不均且边界模糊的问题，图像分割面临巨大的挑战。Kass等人提出主动轮廓模型（active contour model，ACM）并首次应用于图像分割中，利用能量最小化原理，为目标分割提供平滑的轮廓。由于此类模型在处理具有亚像素边缘的图像中表现突出，凭借允许嵌入各种先验知识实现鲁棒分割的优势，在计算机视觉和图像分割中得到了广泛的应用。

目前主要存在基于边缘和区域的主动轮廓模型。前者主要依赖图像梯度信息定义边缘停止函数，在梯度大的位置曲线停止演化，捕捉目标边界。测地主动轮廓（geodesic active contour，GAC）模型为具有代表性的基于边界主动轮廓模型，该模型在高质量图像中取得精确的分割结果，但对噪声敏感且不适合弱边缘的提取。后者主要利用区域统计信息构造驱动力，引导曲线演化至目标边界。根据区域统计信息类型的不同分为基于全局、局部的主动轮廓模型。基于全局的主动轮廓模型中具有代表性的为CV（Chan-Vese）模型，该模型基于图像由两个同质区域组成的假设，能够有效分割同质图像。Zhang等人在CV 模型的基础上提出符号压力函数（signed pressure function，SPF），该函数能够有效阻止轮廓曲线在弱边缘和模糊边缘处的运动，检测目标边界。然而，上述两种模型，难以准确捕捉灰度不均图像的目标边界。为了解决这一问题，Li 等人引入高斯核函数来统计图像局部信息，提出RSF（region-scalable fitting）模型，从而克服全局模型无法分割灰度呈非均匀变化图像的缺点，但该模型对初始化的设置极其敏感，易出现错误的分割结果。鉴于对基于全局和局部两种模型优缺点的分析，许多研究学者尝试将两种模型结合，提出一系列混合模型。Wang 等人引入全局能量项，吸引演化曲线向目标附近靠拢。同时，利用局部能量项进一步驱动演化曲线到达目标边界，该模型在灰度分布较为简单的图像中表现较好，但由于模型中的全局项无法在灰度呈分布不均匀图像中有效识别目标边界，因此即便调节全局项权重系数也难以得到满意的结果。赵杰等人通过设计双核函数来提取局部信息，并使用改进的全局项加以辅助，提出的混合区域主动轮廓模型从模糊C 均值聚类算法（fuzzy C-means algorithm，FCM）中获取目标先验信息，自动设置初始化轮廓。Ding 等人提出优化LoG（Laplacian of Gaussian）能量项，作为一种全局检测方法，与RSF 模型相结合，降低模型陷入局部极值的可能。然而，此模型仍需人工设置初始化轮廓，当轮廓曲线远离目标边界时，演化曲线易受背景干扰，收敛速度缓慢，且局部项的设计仅考虑局部空间信息，无法全面衡量局部邻域点对中心点的影响程度，导致模型在待分割目标弱边缘处易发生泄漏，降低模型的分割精度。

复杂场景中，仅使用主动轮廓模型往往难以得到理想的分割结果。陶永鹏等人通过提取CT 图像的SIFT（scale invariant feature transform）特征，再利用加权随机森林回归算法获取椎骨中心点位置，将其作为CV 分割模型的初始轮廓位置。该方法在自动定位方面具有一定的优势，但无法获取待分割目标形状先验信息。Li 等人提出了一种将模糊C 均值聚类与水平集方法相结合的算法。其中，水平集函数的初始化直接从模糊C 均值聚类中获取，并且从模糊聚类的结果中估计水平集演化的参数，减少了人工操作。Yang 等人使用类似的思想，将模糊聚类的结果作为初始约束信息，通过动态约束项将水平集方法与模糊聚类相结合，提出新的能量泛函。但由于聚类算法在复杂自然图像中表现欠佳，导致主动轮廓模型获取的初始值具有不准确性，从而影响模型的分割结果。视觉显著区域检测算法是当前计算机视觉领域的一大研究热点。Fu 等人提出基于簇的视觉显著性检测算法，通过定义各簇对应的对比度测度和空间测度，来衡量各簇的显著值，并以非线性方式将两个测度融合，得到最终显著图。该模型简单、高效，获取的目标边界清晰，能够在灰度呈不均匀分布的医学图像或自然图像中较好地提取视觉显著区域。Yuan 等人结合回归校正和正则化随机游走排序算法，输出更平滑、准确的显著图。但此类模型仅能定位目标显著区域，难以将目标完全分割出来。

针对主动轮廓模型用于图像分割时，演化曲线受背景干扰，演化速度缓慢，且易在弱边缘处发生泄漏，难以保留目标完整性的问题，本文根据每个簇的紧凑性定义紧凑对比度测度，与空间测度相结合，利用改进显著性检测算法对原始图像进行预处理操作，提取目标候选区域，自动设置初始化轮廓，并将获取的目标先验信息用于优化LoG 能量项的符号选取，自适应决定曲线演化方向；其次，引入局部窗口内邻域灰度信息的变化，设计局部灰度测度，与局部核函数相结合，改进局部能量项，更为全面地衡量局部窗口内邻域像素点对中心点的影响权重，提高模型在目标弱边缘处的敏感程度。此外，本文模型增加长度项和距离正则项，用于平滑轮廓曲线，避免重新初始化。该模型无需人工设置初始化轮廓，并且提升了在目标弱边缘处的捕获能力，取得了更为理想的分割效果。

1 主动轮廓模型简介

1.1 RSF 模型

Li 等人通过定义局部拟合项用于分割灰度分布不均匀图像，提出局部尺度可控的RSF 模型。对于图像域内任意像素点，定义基于水平集函数的局部拟合项，由式（1）给出：

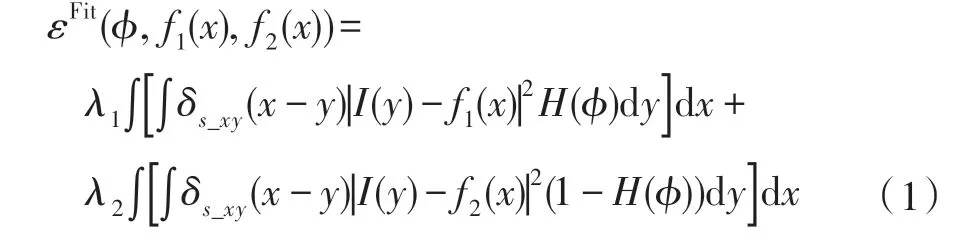
式中，f()为像素点处的局部外（内）拟合均值；、为权重系数，均为正数；δ为高斯核函数，控制局部窗口内邻域像素点处灰度值()对中心像素点处的影响程度；(·)为亥维赛函数。

RSF 模型能够有效分割灰度呈非均匀变化的图像，但由于该模型的局部化特性，导致其对初始化轮廓的设置敏感，曲线演化易陷入局部极值，无法准确定位目标边界，极大程度上限制了该模型的应用。

1.2 ACML 模型

传统LoG 算子对灰度变化十分敏感，在含噪图像中，零交叉点易被判为错误边缘点，构建的能量项用于分割时，易出现“孤岛”区域。为了解决此问题，Ding 等人提出基于图像的优化LoG 能量项，用于平滑同质区域，保持边缘信息，与仅由高斯核函数定义的局部能量项相结合，构建混合模型，本文称其为ACML（active contour model based on optimized LoG and RSF model）模型，降低演化曲线陷入局部极值的可能性。

首先，使用变量来表示优化后的LoG 算子，定义能量泛函，如式（2）所示：

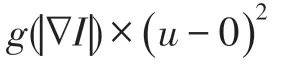
其次，假设待分割目标灰度均值大于背景灰度均值，并使用Ω表示演化曲线包围的内部区域，并用优化后的变量代替文献[20]中传统LoG 算子，构建能量泛函：

最后，使用θ表示全局项系数，结合式（1）、式（3），定义外部能量约束项：

该模型一定程度上避免曲线陷入局部极值。然而，该模型仍需人工设置初始化轮廓曲线，当初始化轮廓设置远离真实目标边界时，曲线容易受背景干扰，演化速度缓慢，且由于局部能量项仅考虑空间信息，使ACML 模型易在弱边缘处发生泄漏，影响模型分割精度和效率。

2 基于视觉显著区域的初始轮廓提取算法

本文结合视觉显著性检测方法获取目标形状先验信息，作为形状约束引入主动轮廓模型中，提出一种基于视觉显著区域的初始轮廓提取算法（initial contour based on visual salient regions，ISR），自动设置初始化轮廓曲线，消除人工干预，初始轮廓曲线于目标边界附近开始演化，避免背景干扰，提高模型分割的精度和效率。

2.1 基于簇的视觉显著区域提取

本文采用基于簇的视觉显著性检测算法获取目标先验信息，并根据各簇的紧凑性对该算法进行改进。首先，使用聚类算法将图像中像素点聚类为个簇，通过统计簇内各像素点到图像中心的空间距离，并比较簇C与其他簇（非簇C）之间的差异性，同时考虑每个簇的空间分布，分别定义空间测度ω(C)和紧凑对比度测度ω(C)。其次，以非线性方式融合两个测度，获取各簇对应的显著值。而后根据每个簇的显著值得到簇中各像素点对应的显著值。

分别定义空间测度ω(C) 和对比度测度ω(C)来表示各簇到图像中心的空间距离以及各簇之间的差异性，如式（5）、式（6）所示：

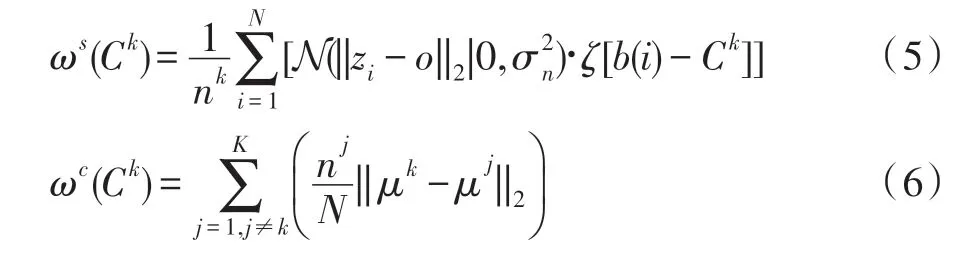
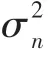
为了更好地抑制背景干扰，获取图像显著区域，文献[21]指出显著目标通常具有紧凑的空间分布，而背景区域较分散。本文将此概念延伸到簇，利用簇内的各像素点到该簇中心位置的空间距离定义紧凑对比度测度，有效抑制背景干扰。首先计算图像域中基于簇的对比度测度显著值均值，如下所示：

其中，表示聚类簇数；使用来表示簇内各像素点到该簇的中心位置的空间距离，并将其归一化为[0,1]。定义如下：

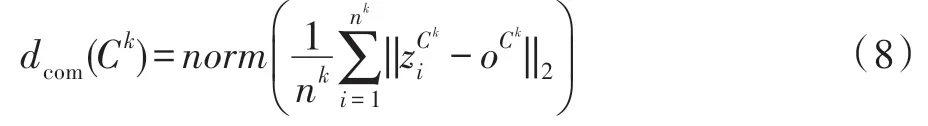
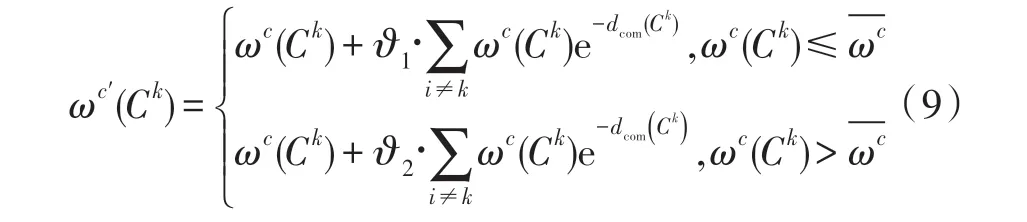
式中，＜，本文所有实验=0,=1。

采取非线性方式融合两种测度，获得更为精确的视觉显著区域，如式（10）所示：

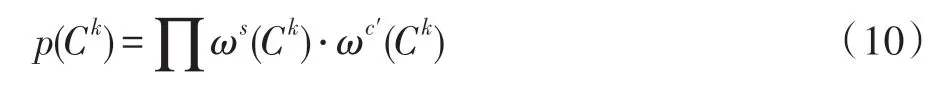
式中，(C)表示簇C显著测度值，每个像素点属于簇C的显著性似然满足高斯分布，定义如下：

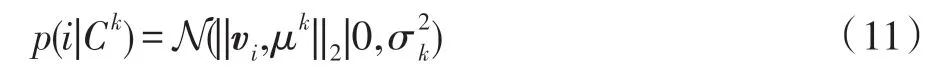
式中，v表示像素的特征向量；μ表示簇C的聚类中心；σ表示标准差。最后获取每个像素点对应的显著值，如式（12）所示：

图1（a）中给出一幅X-Ray 血管原始图像，图1（b）、（c）给出对比度测度与紧凑对比度测度图，再分别与空间测度以非线性方式相结合，获取显著图与紧凑显著图，图1（e）、（f）分别给出其对应的二值图与紧凑二值图，再进一步利用形态学操作滤除孤立区域，获取更为准确的目标形状先验信息。不难看出，使用改进后的对比度测度获取的目标先验信息更加准确，依此设置的初始化轮廓曲线能更好定位目标位置，如图1（d）中绿色曲线所示。

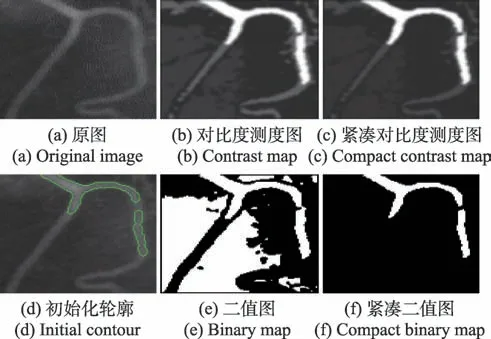
图1 对比度测度改进前后效果Fig.1 Effect of contrast measure before and after improvement

2.2 初始轮廓提取算法

本文结合改进视觉显著性检测算法，获取目标形状先验信息，提出基于视觉显著区域的初始化轮廓提取算法ISR，步骤如下：

1.使用聚类算法将图像聚类为个簇；

2.for←1 todo

根据式（5）计算簇的空间测度ω(C)；

根据式（6）～（9）计算簇C的紧凑对比度测度ω(C)；

end

3.根据式（10）融合两个测度，得到各簇对应的显著值；

4.for←1 todo

根据式（12）获得图像每个像素点对应的显著值；

end

5.根据步骤4 获取待分割图像的视觉显著区域，再利用阈值将获取的显著图分割为二值化图像，当部分目标错分为背景或部分背景错分为目标时，构成图像的两部分（目标和背景）灰度差别越小，反之越大。使用最大化类间方差法来计算最优阈值。将显著值大于阈值的，标签记为1；将显著值小于此阈值的，标签记为0，得到二值图像，对二值化图像进行形态学操作，滤除噪声，将处理后得到的最终二值化图像分界线作为初始演化轮廓曲线。

视觉显著区域的有效提取，能够提供准确的目标先验信息，为后续操作步骤提供可靠依据。本文在提取视觉显著区域特征时，不局限于某一特定的聚类算法，通过实验测试并分析means++、FCM、均值漂移（Mean shift）算法三种较为经典的聚类算法在提取视觉显著区域时的优劣性。

图2（a）～（c）分别给出嵌入means++、FCM、Mean shift聚类算法的视觉显著区域检测算法所获取的初始化轮廓（绿色曲线）。前两种聚类算法均需人工给出聚类簇数，means++算法高效率，易实现，且在改进对比度测度的作用下，降低了对聚类簇数的敏感程度。由图2（a）可以看出，在医学和自然图像中均表现较好。FCM 聚类算法以隶属度来衡量每个数据点属于各簇的可能性，在背景分布相对简单的医学图像中获取较为精确的视觉显著区域，而在背景相对复杂且与目标强度值相近的自然图像中，难以将像素点准确归类，如该算法在小船图像中的分割结果所示。Mean shift聚类算法虽无需人工给出聚类簇数，但引入了带宽参数，当带宽大小设置不合理，收敛速度慢，无法准确地提取视觉显著区域。综合上述分析，本文实验均选取means++算法来获取视觉显著区域，其中簇数为5。

图2 使用不同聚类算法得到的初始化轮廓Fig.2 Initial contour obtained by different clustering algorithms

3 基于混合区域的主动轮廓分割模型

本章首先引入优化变量来代替传统LoG 算子，构建基于图像全局信息的优化LoG 能量项，改善传统LoG 算子对灰度变化敏感的问题，并结合由显著性检测获取的目标先验信息，设计自适应符号函数，对优化LoG 能量项进行加权，自行追踪目标边缘方向；其次，设计局部灰度测度，与高斯核函数相结合，改进局部能量项，更加充分地衡量局部邻域像素点对中心点的影响权重，提高模型对目标弱边缘的敏感程度。此外，引入长度项与距离正则项，用于平滑轮廓，避免水平集重新初始化，提出新的基于区域的混合主动轮廓模型（region based hybrid active contour model，RBHM）。

3.1 自适应符号函数加权的优化LoG 能量项

假设图像由两部分区域组成，且待分割目标灰度均值大于背景灰度均值。考虑到传统LoG 算子对灰度变化敏感问题，同文献[12]，本文使用优化LoG算子来代替Δ，用于平滑同质区域，保持目标边缘，使用表示图像域，定义如下能量泛函：

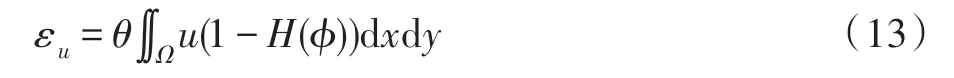
其中，为权重系数，(·)为亥维赛函数。此外，本文利用目标先验信息判断待分割目标相对于图像的亮暗程度，设计自适应符号函数，对优化LoG 能量项进行加权，自行判定目标边缘追踪方向，增强模型自适应能力。

首先，利用改进的视觉显著性检测算法获取目标候选区域，使用大津法对显著图进行二值化操作，并利用圆盘半径为2 的模板对获得的二值化显著图依次进行腐蚀、膨胀操作。类似于文献[24-25]，选取腐蚀后的二值掩码图中最大连通域内的像素点判为目标种子点，标签记为1，其余为非目标种子点，标签记为0，得到目标标签矩阵。其次，对于彩色图像，同文献[26]，选取原始图像（R，G，B）通道中具有最大对比度的位图Img（:,:,cmax），与标签矩阵以非线性方式结合，获取具有最大对比度位图中目标种子强度均值与非目标种子的强度均值，设计自适应符号函数sgn(,)。具体操作步骤如下：

（1）使用(,)表示使用视觉显著性检测算法获取的显著图中像素点，标签矩阵表示二值化显著图经过腐蚀操作后具有最大连通域的二值掩码图，定义如下：

（2）同文献[26]，选取原始分割图像R、G、B 通道中具有最大对比度的位图Img（:,:,cmax），并使用(,)表示位图Img（:,:,cmax）中任意像素点的灰度值，分别计算目标种子点与非目标种子点对应的灰度均值，如下所示：

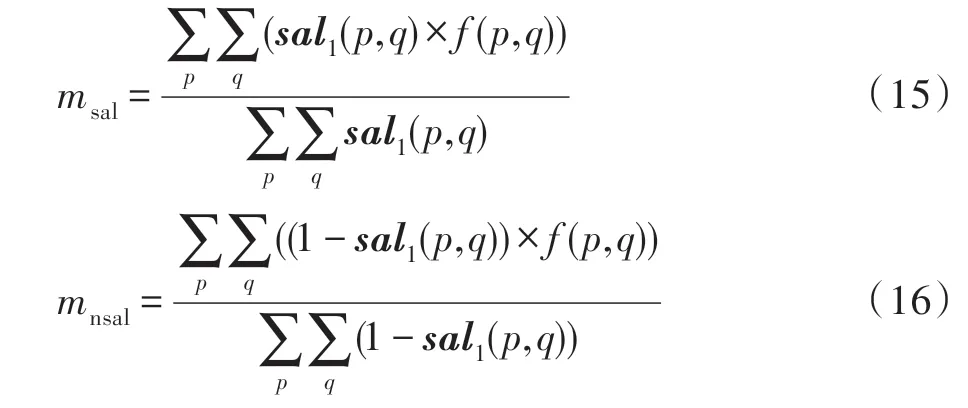
（3）比较目标种子点与非目标种子点的均值大小，设计自适应符号函数，定义如下：

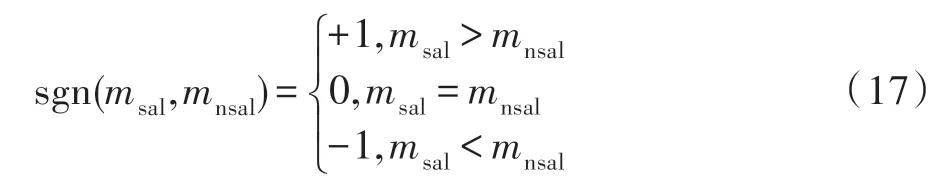
结合式（13）、式（17），本文提出自适应符号函数的优化LoG 能量项，定义如下：

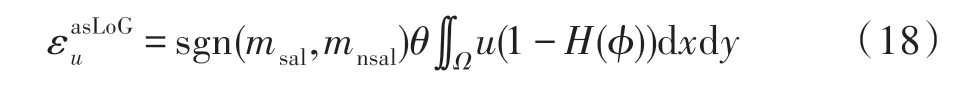
图3（a）中分别给出含有亮、暗目标的两幅合成图像，图3（b）分别为其对应的显著图，图3（c）中黄色封闭曲线所包围的像素点为图像经预处理操作分别获取的目标种子，依此设计自适应符号函数，对LoG能量项进行加权，自行决定曲线演化方向。

图3 目标种子点Fig.3 Seeds of target

不同于基于图像全局信息的CV 模型，自适应符号加权的优化LoG 能量项作为一种全局检测方法，能够在灰度分布不均匀图像中有效识别与背景强度值相差较大的目标边界，自适应决定轮廓曲线的演化方向，避免模型陷入局部极值。然而，仅使用该模型容易出现过分割现象。

3.2 改进局部能量项

本文通过设计局部灰度测度δ，与局部核函数δ相结合，充分考虑局部窗口内邻域像素点对中心点的影响权重，构建新的局部能量项。

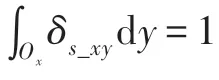
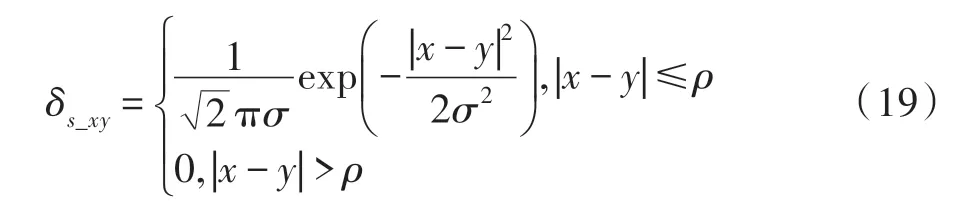
其次，设计局部灰度测度统计局部窗口内中心像素点处的灰度信息变化，当局部窗口位于同质或弱边缘区域，灰度变化较小，应减弱空域中局部邻域点对中心点的影响；当局部窗口邻域点为边缘点或噪声点时，局部窗口灰度变化较大，应增强空域中邻域点对中心点的作用。以此提高模型在弱边缘处的敏感程度，防止错误边缘点出现。

对于图像中的任一局部窗口N，使用ω表示中心像素点所在局部窗口的灰度分布均匀程度，定义如式（20）：

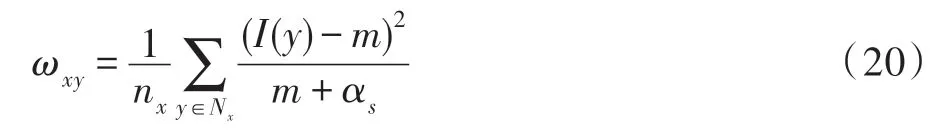
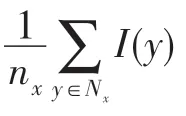
本文采取负指数函数来设计局部窗口内中心像素点处的局部灰度测度，定义如下：

不难看出，当像素点对应的ω值较小时，δ取得较大值；反之，亦然。结合局部灰度变化信息与空间信息改进局部能量项，重新定义式（1）：

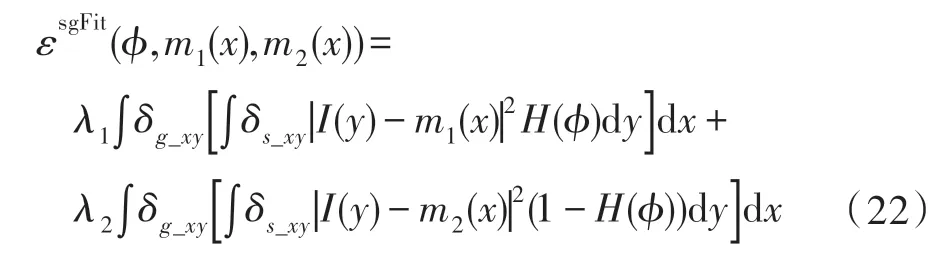
式中，、均为正常数；、表示局部拟合强度均值；()为亥维赛函数，使用正则化函数H()代替计算，其定义如式（23）所示。

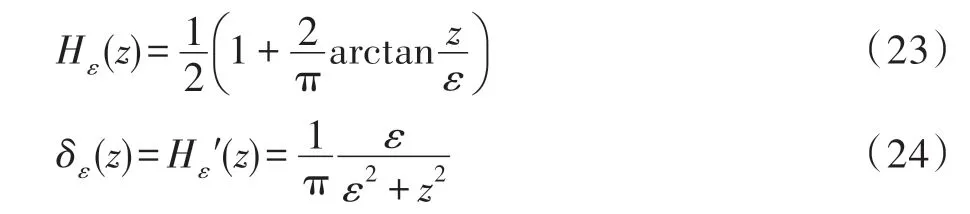
改进的局部能量项在局部灰度统计信息与空间信息共同作用下，能够有效提取目标弱边缘，极大程度上保持了目标轮廓的连贯性与完整性，但对初始化轮廓设置仍然较敏感，且曲线演化易陷入局部极值，无法准确定位目标边界。

3.3 RBHM 模型的提出

鉴于对上述两种能量项的优缺点分析，本文以线性方式将两者结合起来，提出的RBHM 模型在分割过程中能够有效保持目标的完整性，具有较强的自适应能力，能量泛函定义如下：

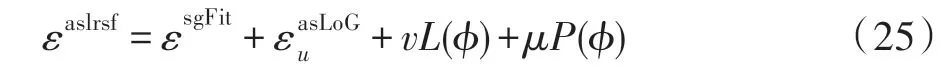
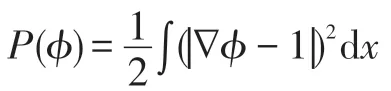
采用同文献[7]中对RSF模型的实现方式，局部均值拟合函数()、()分别通过以下卷积运算获取：

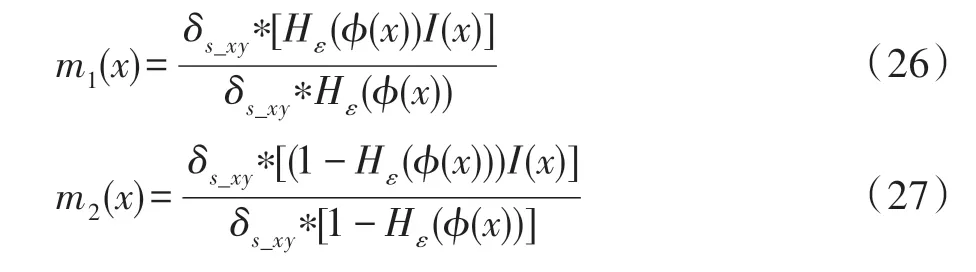
固定()、()，能量泛函（25）关于水平集函数变分，由梯度下降流得到演化曲线，如下所示：

式中，=1,2，∇表示梯度算子；div(·)为散度算子。使用ISR 算法获取的初始化轮廓能够有效识别视觉显著区域，并将提取的目标先验信息用于初始化轮廓的设置与优化LoG 能量项符号的设计，消除人工干预，增强模型自适应能力，而后使用改进的区域拟合能量模型RBHM 引导演化曲线进一步分割。图4（a）给出一幅共聚焦显微镜图像和一幅脑血管造影图像及其初始化，图4（b）给出仅使用高斯核函数定义的局部能量项分割图4（a）中两幅图像的结果，图4（c）为使用局部灰度测度与高斯核函数改进的局部能量项的分割结果，图4（d）为仅使用自适应符号函数加权优化LoG 全局能量项对应的分割结果，图4（e）为本文提出的RBHM 模型分割结果。其中，绿色曲线表示使用ISR 算法获取的初始化轮廓，红色曲线表示分割结果。高斯核标准差=3.3，在分割图4（b）～（e）第一行图像时，长度项系数依次设置为0.000 5 v、0.000 3 v、0.000 1 v、0.000 3 v，在分割图4（b）～（e）第二行图像时，长度项系数依次设置为0.000 6 v、0.000 6 v、0.000 1 v、0.000 6 v，其中v=255×255。

图4 RBHM 模型的有效性Fig.4 Effectiveness of RBHM model

改进的局部能量项由于充分考虑了局部灰度域与空域信息的变化，提高了RBHM 模型在弱边缘处的敏感程度。由图4（c）第一幅图像不难看出，改进的局部能量项在图中弱边缘（黄色框）处的分割结果更加连贯，然而仅使用改进的局部能量项在非边缘目标边界易发生粘连，如该图中（蓝色框处）所示。且在目标分布范围较广的弱边缘图像中，易陷入局部极值，如图4（c）中第二幅图像所示。自适应符号函数加权的优化LoG 能量项由于引入目标先验信息，能够自动追踪目标边界方向，且作为一种全局检测方法，该能量项不易陷入局部极值。考虑到上述两种能量项的优缺点，以线性方式将其结合起来，一方面保持目标轮廓的连贯性和完整性，另一方面降低模型陷入局部极值的可能性，更好地定位目标边界，得到了较为满意的分割结果，如图4（e）所示。

4 基于ISR算法和RBHM模型的图像分割算法

本文首先根据ISR 算法自动获取初始轮廓曲线，而后使用本文提出的RBHM 模型引导曲线继续演化，直至满足迭代停止条件。

本文模型的算法流程图如图5 所示，具体实现操作步骤如下：

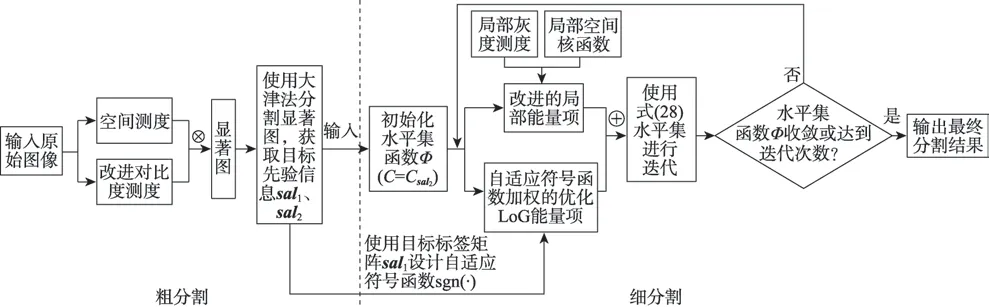
图5 本文模型流程图Fig.5 Flow chart of proposed model

（1）演化曲线常规参数设置：=1，=3.0，局部窗口半径=round(2)，=2，===1，=0.8，Δ=0.02，=0.01，=3，长度项系数需根据图像进行调整。

（2）使用ISR 算法获取图像的初始轮廓，构造水平集函数，即：

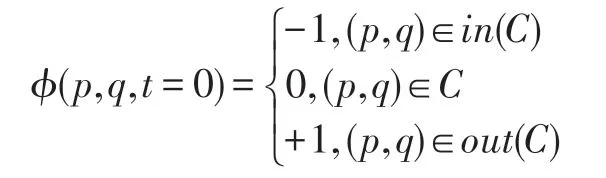
其中，=C。

（3）根据式（14）～（17）设计自适应符号函数sgn(,)，对优化LoG 能量项进行加权，使用式（18）计算自适应符号函数加权的优化LoG 能量项。

（4）根据式（20）～（21）计算局部灰度测度，利用式（22）定义改进局部能量项，再根据式（25）构建新的能量泛函。

（5）根据式（26）～（27）计算局部拟合均值、。

（6）固定、，根据式（28）更新水平集演化方程。

（7）每迭代6 次，计算演化轮廓曲线所围面积的变化，当满足|S-S|＜10或迭代次数＞500，则停止迭代并输出分割结果。

5 实验结果及分析

本文实验均在Intel Core i5-4210U 1.70 Hz CPU，4.0 GB RAM 和Windows 7（64 位）操作系统的个人计算机上完成。编程环境Matlab 2015a。实验中所使用的示例图像选自数据库以及四幅真实示例图像。SPF 模型中的常值速度以及RSF、LGIF、ACML、LPF中的长度项系数～均需根据图像调整，LPF、ACML 模型中时间步长Δ=0.02 。除特殊说明外，其余参数均参考原文设置。

5.1 ISR 算法有效性分析

为了评估自动获取初始化轮廓算法ISR 的有效性，图6 给出六幅真实示例图像，前两幅均为含有弱边缘且灰度分布不均匀的血管图像；第三幅为对比度较低的输卵管造影图像；第四幅为灰度分布极其不均匀且含有弱边缘的茎叶图像；第五幅为一幅含有多目标图像，第六幅为含有极弱边缘的贝壳图像。图6、图7 分别给出六种模型在人工设置的初始化轮廓与使用ISR 算法获取的初始化轮廓下的分割结果。图6、图7 中～表示RSF、LGIF、ACML、LPF 模型中的高斯核标准差，、θ分别表示LGIF模型全局项系数与ACML 模型全局项系数。图6 依次给出人工设置的初始化轮廓曲线（绿色框）及SPF、RSF、LGIF、ACML、LPF 与RBHM 模型分割结果（红色曲线）。表1 为分割图6、图7 时模型中所使用的常值速度与长度项系数值。

表1 分割图6、图7 示例图像时各模型中v、v1～v5 的取值Table 1 Value of v,v1 to v5 in each model segmenting sample images on Fig.6 and Fig.7

图6 人工初始化分割结果Fig.6 Segmentation results of manual initialization

图7 自动初始化分割结果Fig.7 Segmentation results of automatic initialization

由图6 所示分割结果可以看出，使用人工设置的矩形框初始化轮廓做引导，由于SPF 模型仅考虑图像全局信息，在处理灰度分布不均匀的弱边缘图像中，整体效果欠佳；由于RSF 模型仅考虑局部空间变化信息，对初始化的设置十分敏感，在图像4 中出现错误分割结果，且难以将图像中的多个目标分割出来，如该模型在图像5 中分割结果所示；LGIF 模型通过引入全局项对RSF 模型进行改进，在图像5 中取得较优的结果，但仍泄露了部分目标弱边缘，且在分割图像3～4 时，受背景干扰，该模型仍容易陷入局部极值，这是由于该模型中的全局项在灰度不均匀图像中处理能力弱，即便增大全局项系数，也难以准确获取目标边界；LPF 模型在预拟合均值函数的作用下，降低了对初始化轮廓设置的敏感程度。然而，该模型在分割图像4 时，由于背景干扰，出现“孤岛”区域；ACML 模型与RBHM 模型均使用优化LoG 能量项作为全局项，能够在灰度不均匀图像中准确识别目标边界，如在图像3～4 中的分割结果所示。而本文提出的RBHM 模型中的局部能量项充分考虑局部空间和灰度域信息，提高模型在弱边缘处敏感程度，因此在图像6 的极弱边缘处，分割效果明显优于ACML模型。

图7 给出使用ISR 算法自动获取的初始化轮廓（绿色曲线），分别与SPF、RSF、LGIF、ACML、LPF 以及本文提出的RBHM 模型相结合，依次标记为SPF*、RSF*、LGIF*、ACML*、LPF*以及Our（RBHM*）模型。

由图7 各模型的分割结果（红色曲线）易看出，使用ISR 算法获取的初始化轮廓，较人工初始轮廓，各模型分割效果大都得到改善。SPF*模型在某些情况下能够得到部分精确结果，如在图像4～6 中分割结果所示；RSF*模型在灰度不均的图像3～4 以及含有多目标的图像5 中均取得了较为满意的分割结果；LGIF*模型在灰度分布不均的图像3 与图像4 上均得到更为准确的分割结果；LPF*模型在图像3～4、6 上的分割效果也得到改善。ACML*模型与本文（RBHM*）模型不仅能够在图像1～4 上分割出目标，在图像5 中，两种模型均取得更优结果。表2 给出六种模型在人工设置的初始化轮廓与使用ISR 算法获取的初始化轮廓下分割所需迭代时间。

结合表2 和图6、图7 的分割结果，不难看出，利用ISR 算法设置的初始化轮廓曲线，能够准确获取目标先验信息，节省了整体迭代所需时间，提高了各模型分割效率。

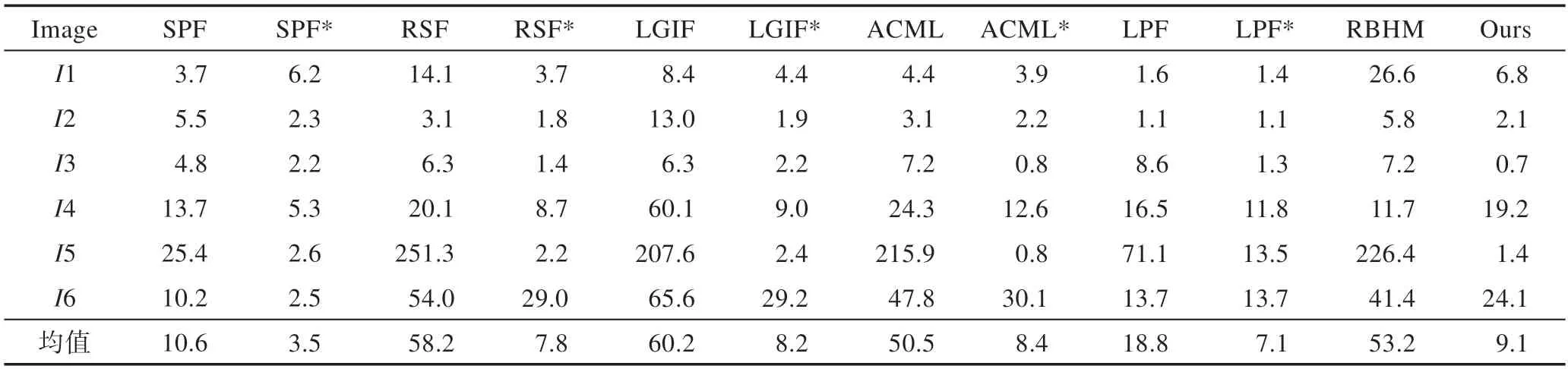
表2 比较六种模型使用不同初始化轮廓所需的迭代时间Table 2 Iteration time required for six models using different initialized contours s

5.2 RBHM 模型的有效性分析

为了进一步验证本文模型分割结果的精确度，引入标准数据库。表3 给出模型分割图8 图像中所使用的常值速度、长度项系数。图8 给出使用ISR 算法自动获取的初始化轮廓（绿色曲线），再依次使用SPF、RSF、LGIF、ACML、LPF模型及本文提出的RBHM 模型对图像进一步分割。

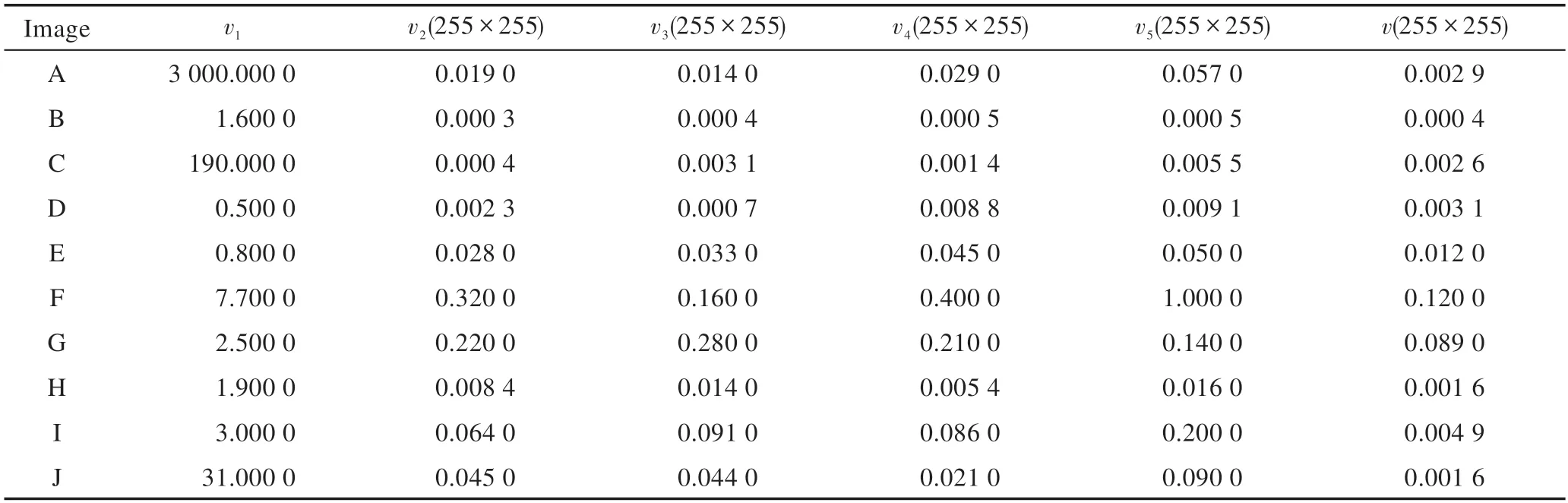
表3 分割图8 示例图像时各模型中v、v1～v5 的取值Table 3 Value of v,v1 to v5 in each model segmenting sample images on Fig.8

由图8 给出的分割结果（红色曲线）可以看出，由于SPF*模型仅考虑全局信息，无法准确贴合目标真实边缘，如在图像I 中的分割结果所示；RSF*模型、LGIF*模型以及ACML*模型均仅利用局部空间信息来定义局部能量项，导致模型在飞机机翼与船桅杆的弱边缘处发生泄漏，且无法提取与背景灰度相似的目标区域，如在图像A～D、I～J 中的分割结果所示；LPF*模型通过计算三通道（R，G，B）的局部强度均值来定义局部预拟合函数，在弱边缘图像分割中表现较好，但该模型对噪声较敏感，如在图像G、J 中分割结果所示。而本文模型在自适应符号函数加权的优化LoG 能量项的基础上，加入了改进的局部能量项，两种能量项的结合不仅增强了模型的自适应性，还能够有效识别噪声点，保留目标弱边缘信息，如在图像E～F、H 中分割结果所示，在图8 示例图像中获得的分割结果与真实目标边界更为接近，其中在分割图像G 时，迭代次数为1 700。

图8 六种模型分割结果Fig.8 Segmentation results of six models

采用骰子相似系数（dice similarity coefficient，DSC）、Jaccard 相似系数（Jaccard similarity coefficient，JSI）、Hausdorff 距离（Hausdorff distance，HD）三种指标来进一步衡量各模型分割结果的质量，定义如式（30）～（32）所示。

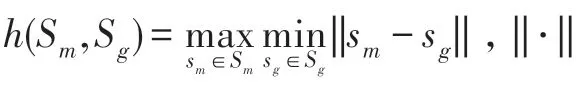
表4 和表5 分别给出六种模型在图8 示例图像分割结果对应的DSC、JSI 与HD 的值。结合表4、表5数据及图8 的实验结果可以看出，本文模型能够在背景复杂及灰度呈非均匀分布的图像中有效提取目标弱边缘，且本文模型分割每幅图片平均迭代时间为16.0 s，与分割效率最高的SPF*模型仅12.1 s 之差，而本文模型取得了更精确的分割结果。考虑到马氏距离不受量纲的影响，因此在计算簇与簇之间的差异性时，使用马氏距离对图7、图8 中图像进行测试，部分图像无法获得准确的目标先验信息，这可能是在计算马氏距离时，放大了变化微小的变量作用，导致提取的视觉显著区域不够准确，寻找一种更加有效的距离度量方法来提取视觉显著区域也能够在一定程度上提高本文模型的分割精度。

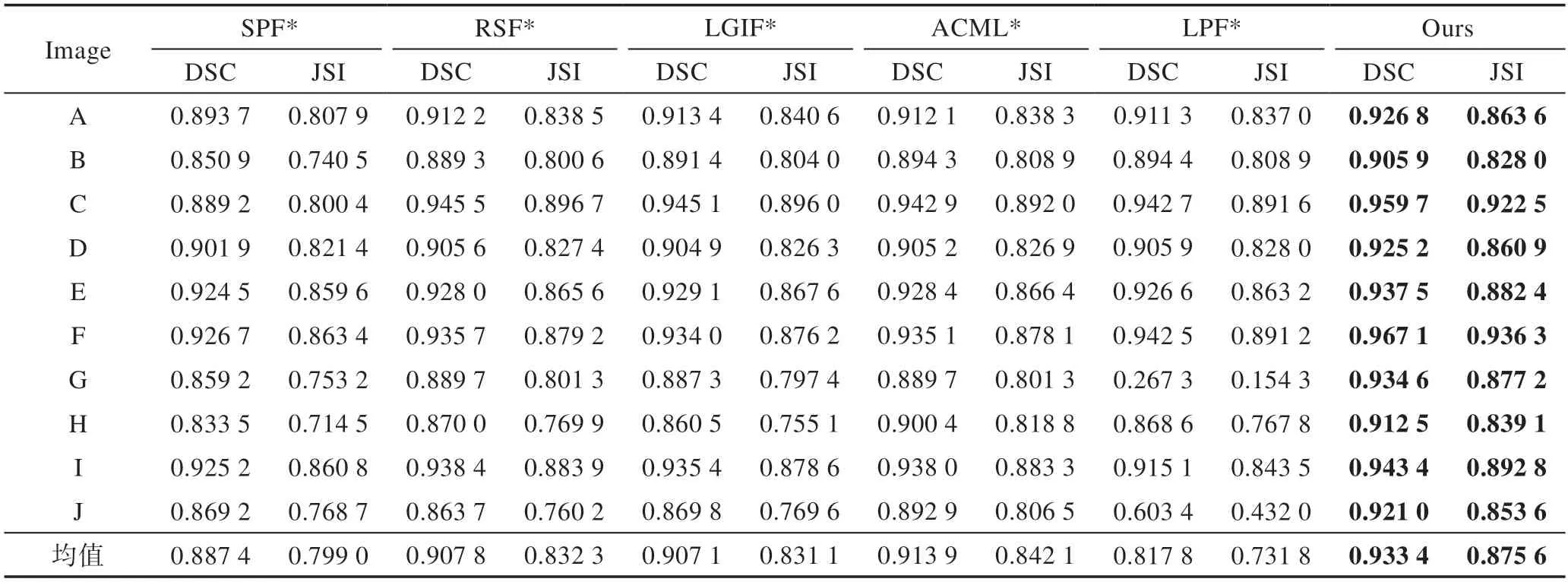
表4 六种模型在图8 图像上的分割精度Table 4 Segmentation accuracy of six models on Fig.8

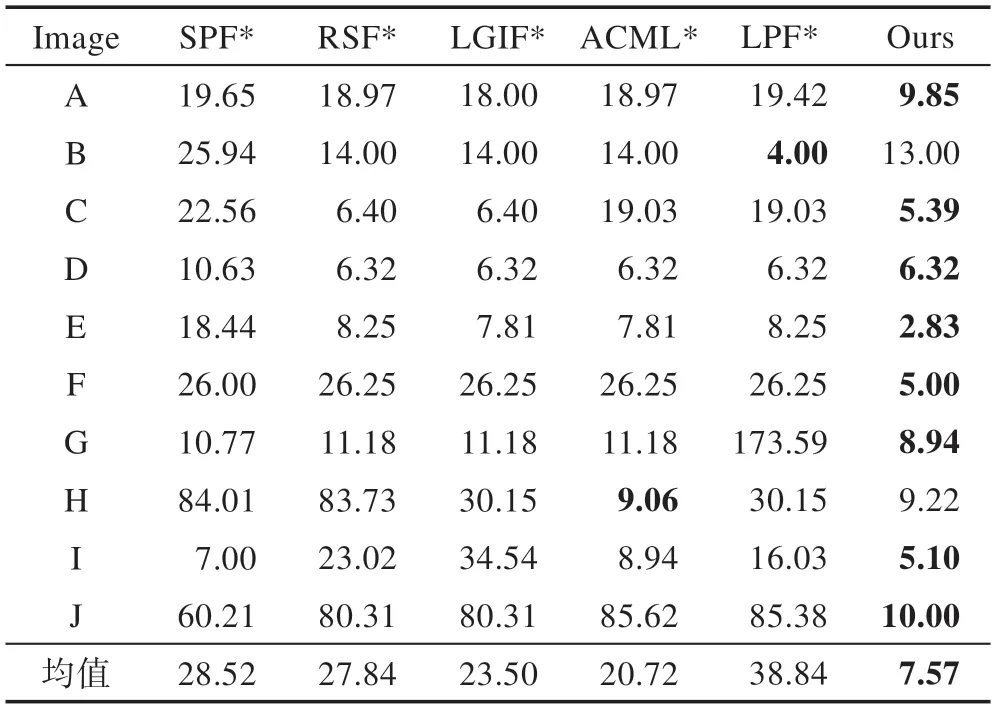
表5 六种模型在图8 图像上的分割评价（HD）Table 5 Segmentation evaluation of six models on Fig.8(HD)

6 结束语

本文结合改进的视觉显著性检测算法，为初始化轮廓的设置提供可靠的依据，并将获取的目标先验信息用于自适应符号函数的设计，对优化LoG 能量项进行加权，提出自适应符号函数加权的优化LoG能量项，并与改进的局部能量项以线性方式相结合。一方面，提高模型在弱边缘的敏感程度，保留目标轮廓的连贯性与完整性；另一方面，降低模型陷入局部极值的可能，增强了模型的自适应能力。接下来，将进一步优化显著图提取算法，为主动轮廓模型中的曲线演化提供更准确的先验信息。