高斯混合生成模型检测健康数据异常

朱壮壮，周治平

江南大学 物联网工程学院，江苏 无锡214122

近年来，人们对健康的生活方式越发重视，越来越多的人通过运动手环来监测自己的健康。运动手环可以监测人们的运动状况和一些行为方式，如睡眠时长、心率和运动步数等。Lim 等人发现患有疾病的手环佩戴者和健康佩戴者的手环数据存在显著的差异，且特定指标与特定疾病的关联较大，如运动步数和静息心率这两个指标都与心血管疾病和代谢紊乱有关。对于手环佩带者而言，在对数据缺乏有效分析的情况下，仅仅依靠手环显示的信息并不能准确地了解其身体的健康状况。对于手环收集到的数据，异常值是指与某些疾病相关联的指标偏离个体基准的数据。因此有必要找出手环数据中的异常值，提前判断出用户身体是否存在隐患，以便提前做出相应治疗，这对改善用户身体健康有重大的作用。

基于距离的异常值检测方法，包括近邻（nearest neighbor，NN）和平均近邻，主要是基于对全维空间中距离的评估，该方法假定异常点与正常点之间的距离较远，因此计算每个样本点之间的距离（或者平均距离），并与距离阈值比较，若大于阈值则视为异常点。然而，当处理高维数据时，相关距离和近邻的概念变得没有意义，异常检测的效果也变差。在这个大数据时代，数据呈现高维度特征，使得在进行异常检测时，容易出现“维度灾难”问题。为了解决该问题，许多研究都集中在基于降维的异常值检测方法上。传统的技术采用两步法，即先降维，再进行异常检测，这两个步骤分别训练，在没有异常检测指导的情况下进行降维训练，容易丢失异常检测的关键信息。Zhou 等人将深度神经网络（deep neural network，DNN）降维和均值（-means）聚类方法结合起来，便于同时优化这两个任务，减少解耦学习的影响，提升检测效果。

深度学习领域的学者们已经提出了多种异常检测技术用以改进检测性能。Zong等人提出了DAGMM方法，该方法首先利用深度自编码器将原始数据进行潜在空间表示，并将低维特征表示和重构误差特征输入GMM（Gaussian mixture model）中进行密度估计，通过选择合适的密度阈值，将密度高于该值的数据记为异常值。然而，该方法假设异常是不可压缩的，因此不能从低维潜在空间中有效重建输入数据。相较于VAE 使用重建概率重构原始数据，重构误差缺乏客观性，导致DAGMM 方法检测性能不佳。与GMGM（Gaussian mixture generative model）类 似，Nalisnick 等人提出了将VAE（variational autoencoder）与GMM 结合在一起的DL-GMM 方法，它采用混合高斯分布近似VAE 的后验，从而提高了原始VAE 的容量。但是，它不适用于无监督的异常值检测。Liu等人提出了一种基于多视图主题模型的异常检测方法，该方法利用多视图主题模型对原始数据中的特征进行建模得到对应的关系，能够大大降低检测的误报率，但是该方法检测准确性偏低。

鉴于此，本文利用GMGM，用以进行人体活动数据的异常检测。在该模型中，使用生成模型中的VAE生成数据潜在分布和重构误差来训练DBN（deep brief network），以预测样本的混合成员隶属度。高斯混合模型通过样本的混合成员隶属度预测得到每个数据的样本密度，将密度高于训练阶段阈值样本视为异常。GMGM 共同优化了VAE、DBN 和GMM，从而避免了模型解耦的影响。

本文有三个主要的贡献：

（1）为了尽可能保留原始数据的特征，生成网络利用VAE为原始样本生成潜在分布和重构误差特征。

（2）为了避免在计算样本密度过程中，由于矩阵的奇点问题导致协方差矩阵无法求解，GMGM 利用样本的混合概率、均值和协方差来构造协方差矩阵的Cholesky 分解，以计算样本密度。

（3）由于传统的两步法技术在进行异常检测时会丢失关键信息，GMGM 以一种端到端的方式共同优化VAE、DBN 和GMM，以保留数据的原始特征。

基于该方法，文本实现了健康数据的异常检测，并在真实数据集上进行了实验，结果表明，所应用算法可以有效地检测健康数据中的异常。

1 相关工作

1.1 变分自编码器

变分自编码器的提出，旨在解决传统的算法处理复杂场景中推断和训练困难且耗费大的问题，它能够生成输入数据潜在变量的低维表示。变分自编码器可以看作一个特征器，根据原始样本分布，构建出其概率分布以重构数据。相比深度自编码器采用重构误差进行重构数据，重构概率是一种概率测量，它考虑了变量分布的可变性，比重构误差更具原则性和客观性。因此，本文选取VAE 进行特征提取，解决“维度灾难”问题，同时保留原始数据的多模态特征。近年来，变分自编码器逐渐与深层神经网络结合，通过隐含层的堆叠以一种无监督的方式进行参数优化。假设∈R表示一个维度为的向量，∈R表示对应的维度为′的潜在表示，(·)表示概率分布函数，则概率分布的生成过程可以表示为：

1.2 高斯混合模型

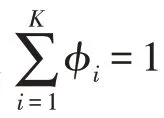
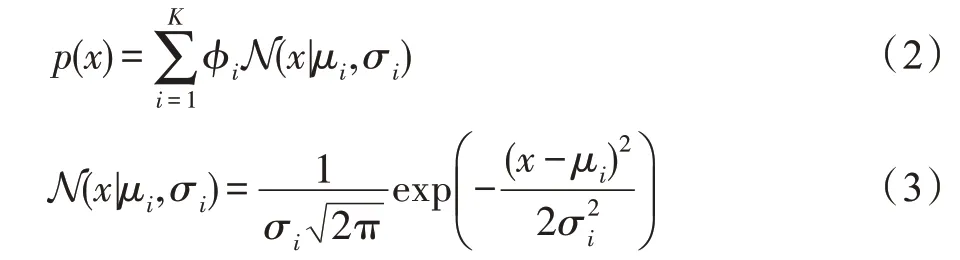
GMM 模型训练阶段，使用EM 算法以最大化似然函数的方式求解模型最佳参数，即混合概率φ、均值μ和协方差σ，直至模型收敛。

2 本文算法

针对GMM 对高维数据进行密度估计时，会出现时间复杂度较高的问题，本文利用GMGM 对健康数据进行异常检测。如图1 所示，该模型主要由两部分组成：生成模型和高斯混合模型。GMGM 的工作原理如下：首先，生成模型通过VAE 对输入样本进行降维处理，以便生成样本点的潜在空间表示和基于重构的特征提供给DBN；接着，DBN 采用馈送，预测得到样本点的混合成员隶属度；最后，利用混合成员隶属度，GMM 预测每个数据的样本密度，将样本密度高于训练阶段的阈值的数据视为异常。

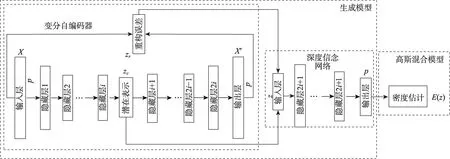
图1 高斯混合生成模型结构示意图Fig.1 Structure diagram of Gaussian mixture generative model

2.1 本文算法

在高维空间中，会出现一种“维度灾难”的现象，即随着数据维度的增加，密度预测的时间复杂度会急剧增加，性能下降。为了解决此问题，生成模型通过VAE 对数量为，维度为的输入数据=[,,…,x]∈R进行重构处理，提取样本点的潜在空间表示和重构特征，以保留样本的固有多模态信息，并将其作为DBN 的输入。

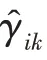
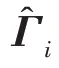
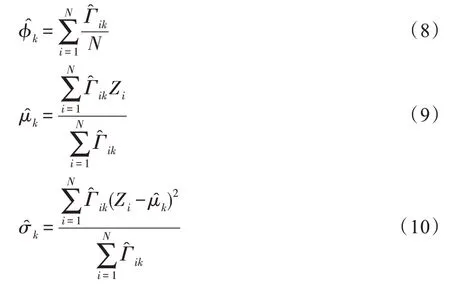
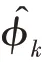
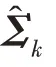
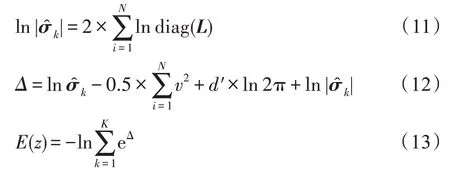
传统的两步法技术在进行异常检测时会丢失关键信息，因此需要将降维过程与密度估计过程联合训练，相互优化。GMM 在利用EM 算法进行模型训练时，首先根据当前参数计算每个数据的混合成员隶属度，接着利用得到的混合成员隶属度计算模型参数，直至收敛。因此，本文中GMGM 将期望最大化算法的E 步骤中的样本属于各子分布的概率替换为端到端结构中生成模型的输出，以一种端到端的方式共同训练了生成模型与GMM；接着，利用EM 算法中M 步对GMM 中的均值、协方差等做参数估计，然后极大化似然函数，相对于传统的训练方式，更易达到理想的检测效果。

在测试阶段，GMGM 可以根据式（13）预测样本的密度，将样本密度高于训练阶段阈值的数据视为异常。

2.2 目标函数

由于解耦学习性能不佳，在GMGM 中，将VAE、DBN 和GMM 统一起来，共同进行模型训练。给定个数据点的样本集，目标函数如下：

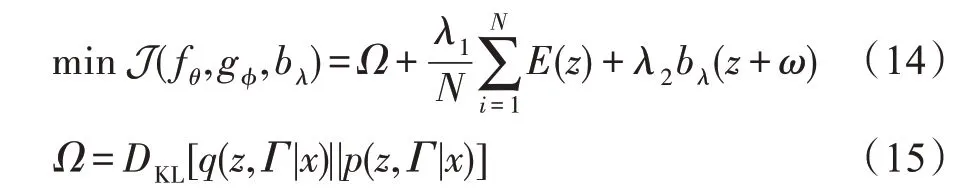
式（15）表示后验分布(,|)和最大似然分布(,|)的KL散度。通过最小化后验分布与最大似然分布的KL散度，以最大程度地提高多维输入的似然。

()模拟可以观察输入样本的概率。通过最小化样本密度，以最大化观察到输入样本的可能性，以便得到VAE、DBN 和GMM 参数的最佳组合。

和是用于规范目标函数的超参数，实验中，=0.1，=0.001 通常可以得到较好的结果。最小化J(f,g,b)可为生成模型和GMM 提供最佳的参数组合。

2.3 算法复杂度分析

假设∈R表示数量为，维度为的原始输入数据，GMGM 方法需要对原始数据进行重构处理，设定隐含层层数为3，即三层编码器、三层译码层，′为设置的各隐藏层节点数（即每层输出维度）中的最大值，该部分的时间复杂度为(′)；DBN分别预测各样本属于个组件的概率，该部分包括反向传播过程和Softmax 过程，该部分的时间复杂度为(′)；利用GMM 进行密度估计，该步骤的时间复杂度为((+1))，因此GMGM 的时间复杂度为((+1)+(+1)′)。随机异常选择（stochastic outlier selection，SOS）算法采用相异度矩阵以亲和力的概念量化两点之间的关系，其时间复杂度为()，远高于本文算法；经典的异常检测算法如VAE，其时间复杂度为(′)，DAGMM 时间复杂度为((+1)+(+2)′)。

3 实验评估

实验平台配置为Windows10 操作系统、Intel Core i7-7700HQ CPU 处理器、2.80 GHz、20 GB 内存，所有算法由Python 实现。

本文选取了5 个数据集，皆来自ODDS 数据库，这些数据集包含异常类，并根据样本标签区分。标签为0 的数据为正常类，标签为1 的数据为异常类，数据集的数据特征见表1。

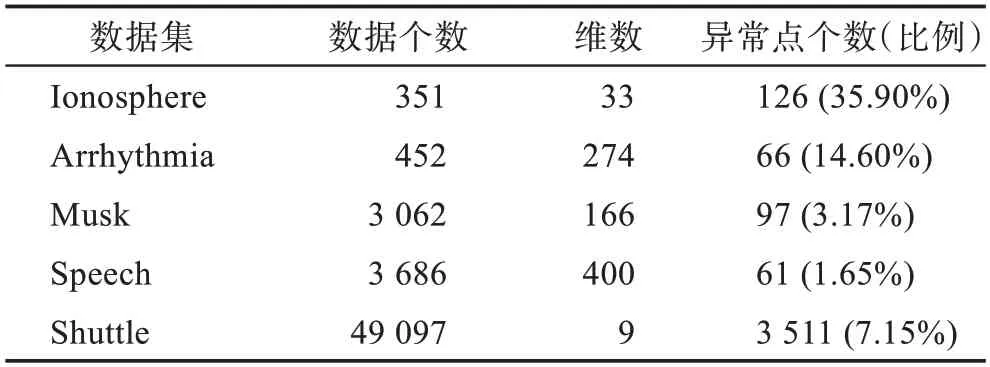
表1 数据集信息Table 1 Dataset information

为验证算法性能，将本文算法与SOS、基于变分编码器的异常检测算法、深度自编码器高斯混合模型（deep autoencoding Gaussian mixture model，DAGMM）进行了比较。选取的原因是：SOS 算法使用关联的概念来计算每个数据点的异常值概率，这与本文预测每个样本点密度的方式类似；本文算法是基于变分自编码器的异常检测算法的改进，因此选取其作对比；DAGMM 采用深层自编码器提取原始数据的特征，通过多层感知机估计样本的混合成员隶属度，最后通过GMM 计算每个样本点能量进行异常检测，其检测效果较好，并且结构与本文算法相似，因此选取其作为对比算法。

本文所用的评估异常检测算法的性能指标是：召回率（Recall）、1分数（1-Score）、正确率（ACC）和受试者工作曲线（area under curve，AUC）。较好的异常检测算法应该有较高的Recall、1-Score、ACC、AUC。

3.1 实验对比结果与分析

对于各样本集，GMGM 的参数设置如下：数据集Ionosphere、Arrhythmia、Musk、Speech 和Shuttle 的潜在空间表示维度分别为3、4、4、4、2；为了确定GMM最优组件的个数，需要使用一些分析标准来评估模型的可能性。本文参考了文献[6]与文献[7]，发现其主要是采用了贝叶斯信息准则（Bayesian information criterion，BIC）的评价方法来确定组件个数，模型的BIC 值越低，GMM 预测样本数据样本密度的性能越好。对于本文中所有的数据集，GMM 组件个数取3时，模型BIC 值最小，因此对于所有的数据集，GMM组件个数设置为3。

为了验证GMGM 针对高维数据检测性能的优势，选取了维度较大的Speech 数据集，采用定性的方式，与SOS、VAE 和DAGMM 算法进行ROC 曲线的对比，对比结果如图2所示。从图中可以看出，相较于SOS、VAE和DAGMM算法ROC曲线下面积AUC值，GMGM异常检测方法的面积最大，即AUC值最高。其中，VAE 算法的检测效果最差，可能是因为VAE 在对数据进行潜在空间表示的时候，把原始样本跟异常有关的关键信息错误地进行了删除，导致检测AUC值较低；而GMGM 采取的是端到端的联合训练，可以同时训练VAE、DBN 和GMM，使三者模型参数达到最优，检测效果较为理想。

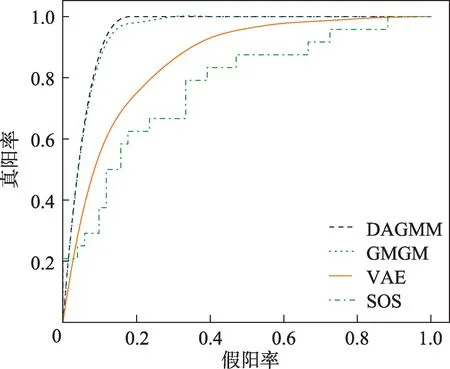
图2 各算法检测Speech 数据集的ROC 曲线Fig.2 ROC curves of each algorithm for Speech

从图3 中可以看出，对于不同的数据集，本文算法在取得最好的检测效果时，所对应的VAE 编码器层数都不同。当值增大时，各数据集对应的AUC值总是先增大后减小。这是因为先增大值可以使得编码器很好地进行数据重构，较好地学习到原始样本的特征，因此AUC 值增大；但是之后随着继续增大，导致训练过拟合，使得算法AUC 值减小。经过综合考量，对图3 中5 个数据集的值选择分别是4（33-16-8-3）、5（274-136-64-16-5）、5（166-84-42-12-5）、5（400-200-100-50-5）、2（9-2）。

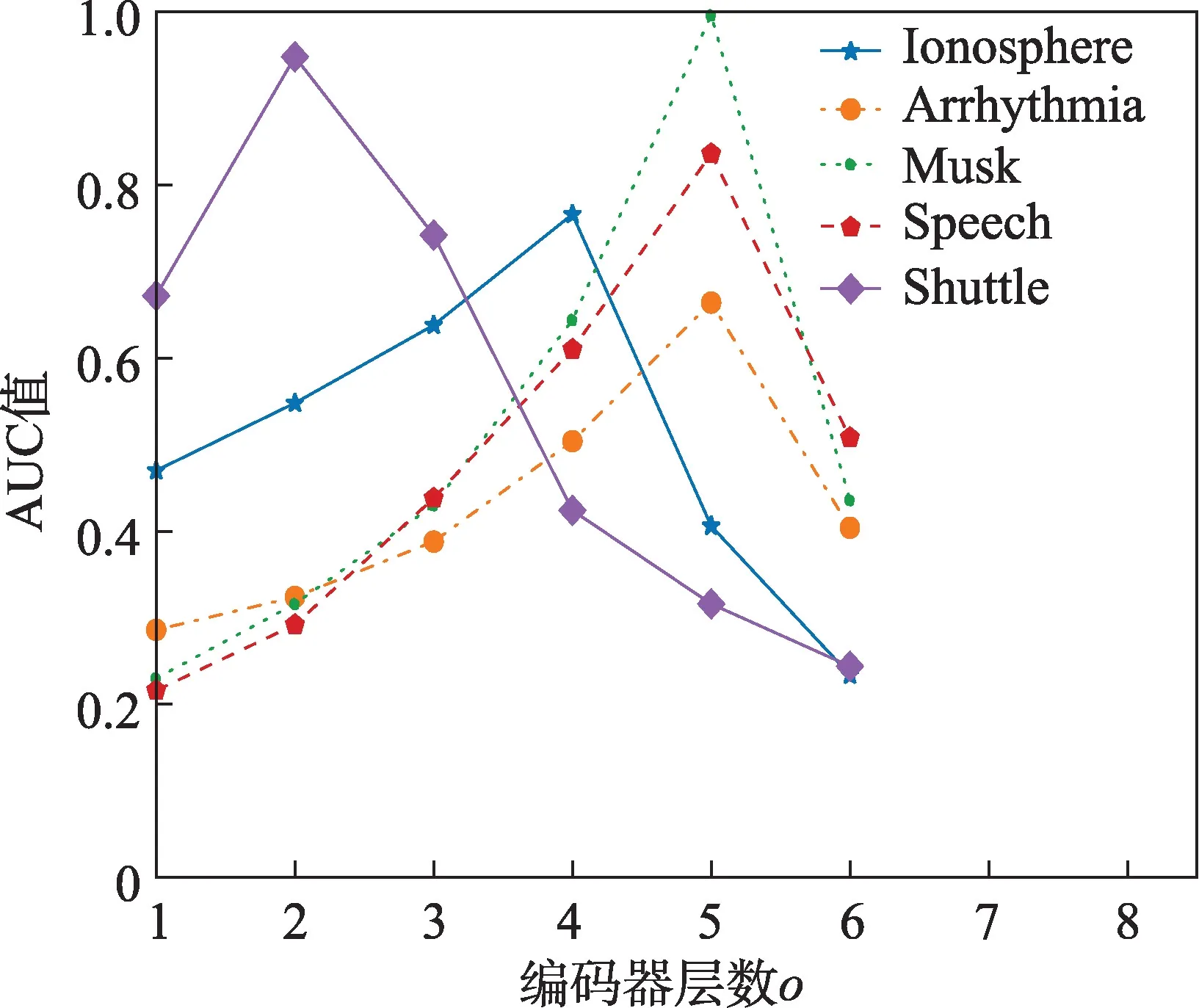
图3 各数据集在GMGM 上的不同o 对应AUC 值Fig.3 AUC curves with different o for different datasets on GMGM

为了验证GMGM 在时间复杂性上的优势，将其与SOS 算法、VAE 算法和DAGMM 算法的平均检测时间进行对比，对比结果如表2 所示。

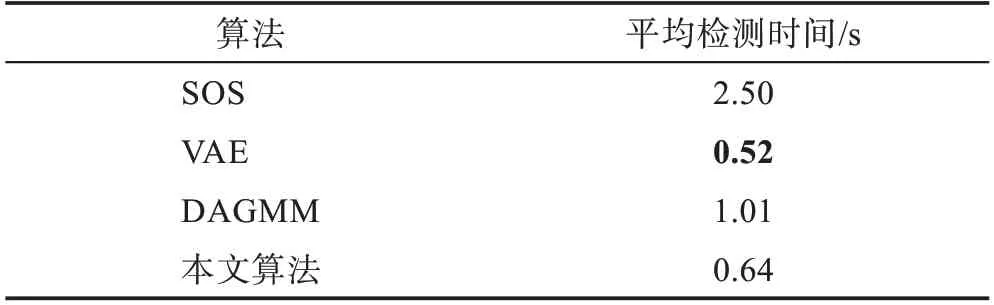
表2 各算法平均检测时间对比Table 2 Comparison of average detection time of each algorithm

从表2 可以看出，虽然本文算法的平均检测时间不是最低，但是比平均检测时间最低的VAE 算法仅相差了0.12 s；并且其平均检测时间比性能较好的DAGMM 算法提升了37%，体现了本文算法在检测时间方面的优势。

为了验证本文端到端结构的有效性，将本文算法与独立训练的模型进行对比，实验结果如表3 所示。从表中可以看出，采用端到端训练的GMGM 的各个指标均高于独立训练的模型。

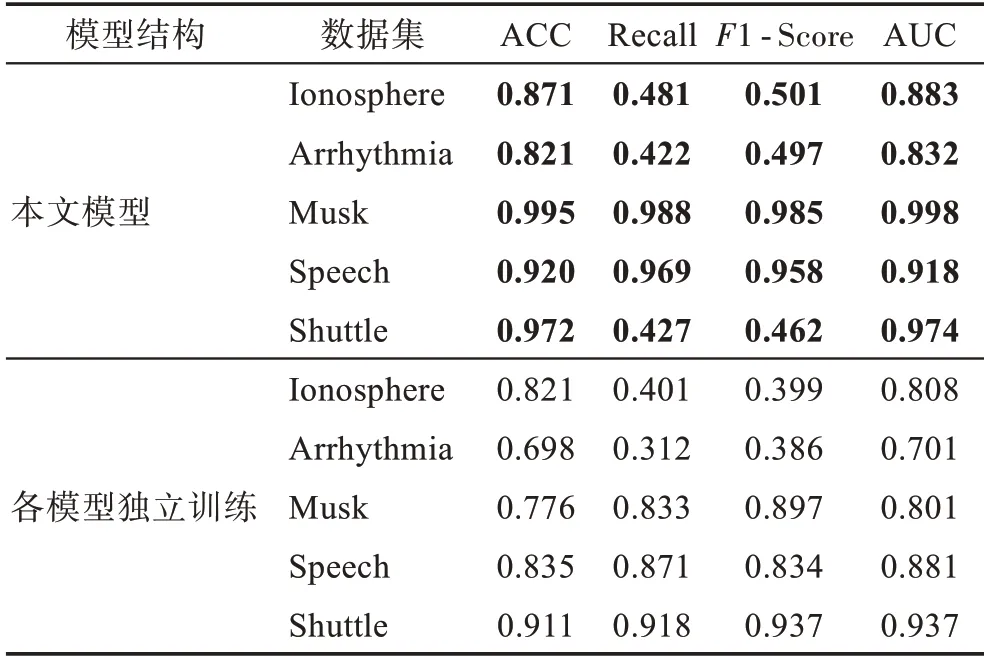
表3 不同模型结构实验结果对比Table 3 Comparison of experimental results of different model structures

为了验证本文算法性能的优势，将本文算法与VAE 算法、SOS 算法和DAGMM 算法进行对比，计算各异常检测算法性能指标ACC、Recall、1-Score 和AUC值，列入表4中。其中VAE算法的隐含层层数和各层节点数与生成网络中的VAE 相同；DAGMM 与文献[6]具有相同的参数设置。

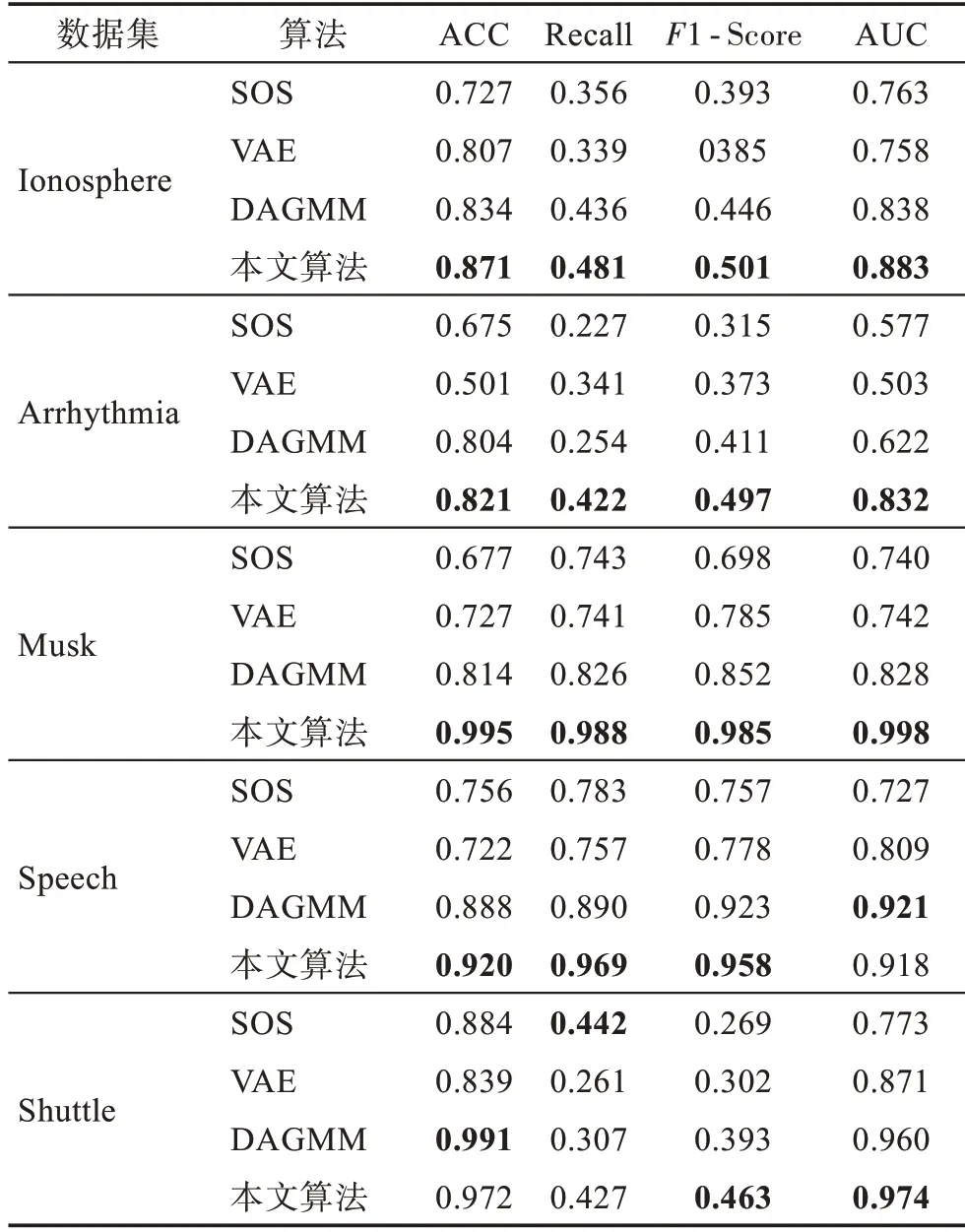
表4 不同算法实验结果对比Table 4 Comparison of experimental results of different algorithms

从表4 的对比实验结果可以看出，GMGM 的准确率仅在大数据集Shuttle 上稍低于DAGMM 算法；其AUC 值也仅在Speech 数据集上稍低于DAGMM算法；在大数据集Shuttle 上的Recall 值虽然不是最高，但与最高值相差不多；在高维数据集Musk 上准确率达到了0.995，远高于SOS 算法的0.677，在维数较高且数据量较大的Arrhythmia 数据集上也表现出较为理想的检测效果；在Shuttle数据集上，虽然本文算法的ACC 和Recall 稍有降低，但是1-Score 与AUC值分别提高了7 个百分点与1.4 个百分点。这种情况发生的原因可能是，算法中的潜在空间表示能够较好地捕捉到数据的整体特性，提高了数据的局部结构能力，降低了算法的时间复杂度；但同时，VAE 在对大数据集Shuttle 进行潜在空间表示的时候，由于数据量比较大不可避免地会出现过拟合现象，这也是本文算法需要改进的地方。

3.2 健康数据异常检测结果

算法的性能得到了验证之后，利用该算法在收集到的健康数据上进行实验，对异常值进行检测。图4是采用本文算法进行异常检测可视化的结果。其中黑色点表示正常数据，红色点表示异常数据。

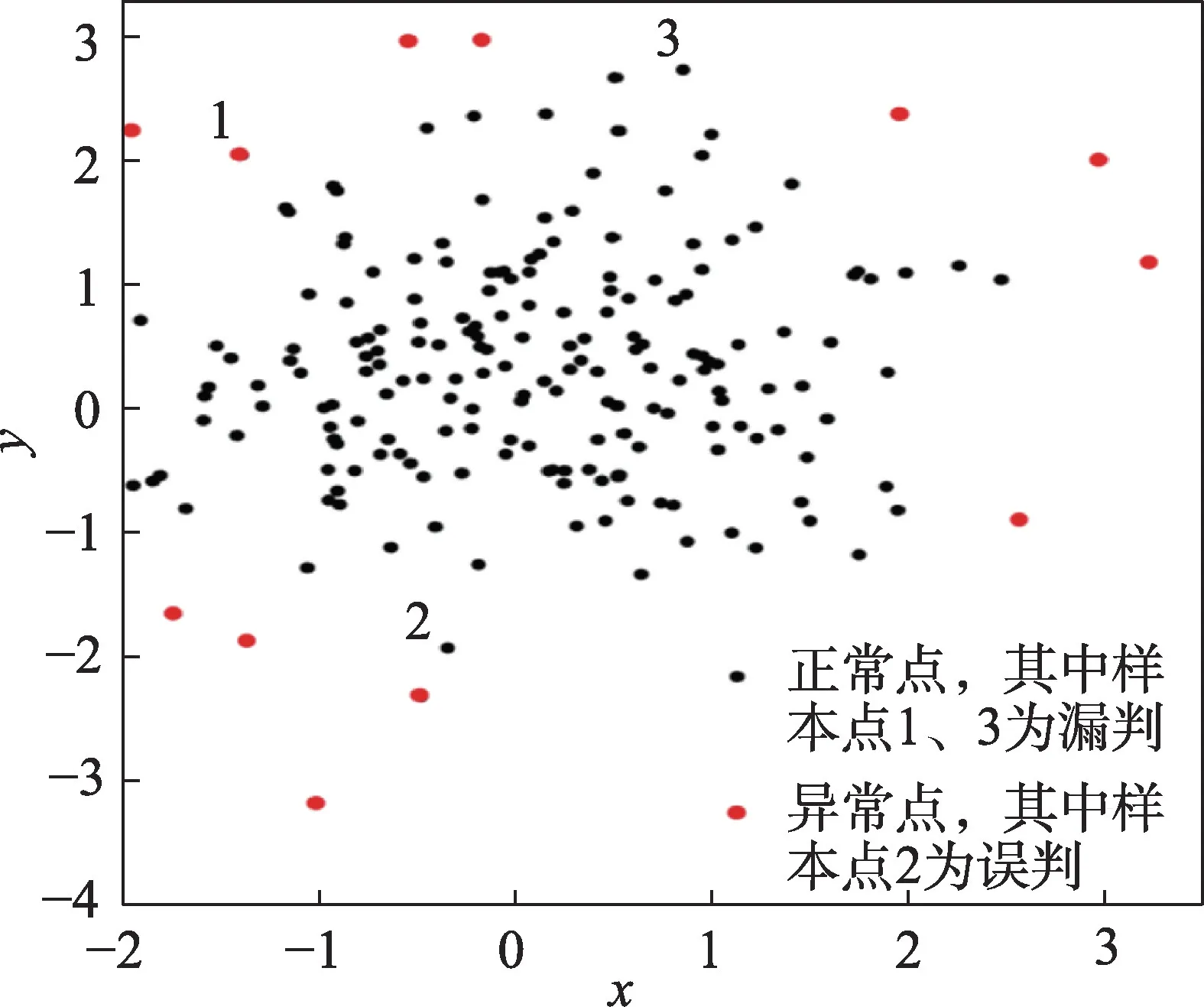
图4 GMGM 算法在健康数据上异常检测结果Fig.4 Detection results by GMGM on health data

为了突出该算法的优势，又采用了检测效果同样好的DAGMM 算法在同一实验环境下对同样的健康数据进行了实验，结果如图5。

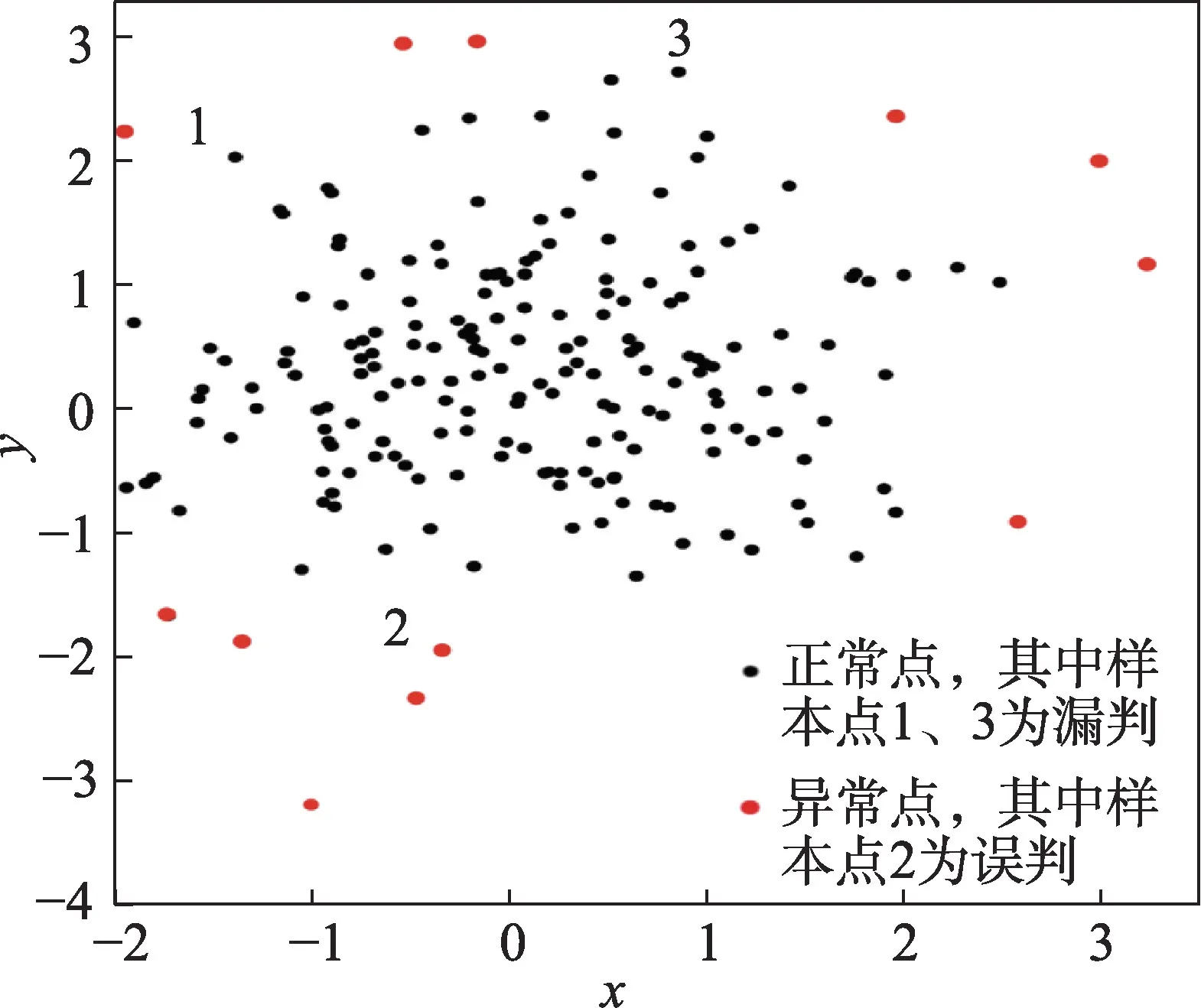
图5 DAGMM 算法在健康数据上异常检测结果Fig.5 Detection results by DAGMM on health data

对比图4 和图5 可以看出，两种检测方法对于比较明显的异常样本点都可以检测出来，但是DAGMM算法在数据边缘存在误判和漏判现象。标号为1、3的样本点为漏判，标号为2 的样本点为误判。而本文算法在检测边缘异常点时，仅3 样本点进行了漏判，整体性能较好。

4 结论

针对运动手环采集的活动数据存在未知异常数据的问题，利用GMGM 用以进行异常检测。在该模型中，使用生成模型中的样本潜在分布和重构特征来训练DBN，以估计各样本的混合成员隶属度；接着，利用GMM 预测各样本的密度进行异常值的检测。生成网络与GMM 共同优化，避免了模型解耦的影响。在实验部分，采用具有代表性的异常检测数据集进行实验，结果表明，该方法具有理想的检测效果。最后，利用该方法在真实数据集上可视化异常检测结果，结果表明漏报率和误报率均低于DAGMM算法。