核中心驱动混合蛙跳算法及其应用

刘立群，顾任远

甘肃农业大学 信息科学技术学院，兰州730070

容量限制车辆路径问题（capacity-limited vehicle routing problem，CVRP）是车辆路径问题（vehicle routing problem，VRP）中最常用的一种。CVRP 是典型的非确定性多项式（non-deterministic polynomial，NP）难解问题，现有技术大多采用启发式算法求解，但均存在算法运行时间长、易于陷入早熟收敛现象的缺陷。在CVRP 中，所有客户的服务类型相同，同为送货或同为收货，所有车辆载重量一样，每个客户的需求量均不大于车辆载重量，车辆都从配送中心出发最终也返回到配送中心。

混合蛙跳算法（shuffled frog leaping algorithm,SFLA）是一种新的基于全局搜索和局部更新的启发式合作搜索算法，它模仿了青蛙在受限环境中的觅食机制。该算法具有参数少，全局寻优能力强和较快的收敛性等优点，在组合优化问题等方面获得了较好的效果。但是SFLA 在寻优更新中，存在差异更新随机性，导致SFLA 在进化后期易出现收敛速度慢、精度低等问题。目前，已有诸多学者对SFLA 的寻优策略进行改进，性能得到了较好的改善。文献[9]把具有极强局部搜索能力的幂律极值动力学优化结合如SFLA，提出基于实数编码模式的混合蛙跳算法求解容量约束车辆路径问题。文献[10]将改进后的SFLA 采用实数编码方式，融入自适应差分扰动机制及混沌局部搜索策略到局部搜索过程用于求解带有容量约束的车辆路径问题。文献[11]针对带容量约束的车辆路径问题，提出了一种带分裂机制的帝国竞争算法进行求解。文献[12]提出了一种量子行为粒子群优化算法和探索启发式局部搜索算法来求解容量约束的车辆路径模型。文献[13]将容量约束的车辆路径问题扩展到更广泛的度量空间。文献[14]定义了离散的蝙蝠位置、速度、频率以及更新规则，用于解决带容量约束问题的车辆路径问题。文献[15]提出一种离散布谷鸟算法求解带容量约束的车辆路径问题。文献[16]对粒子群与改进蚁群算法进行融合改进，并应用于三维路径规划（autonomous underwater vehicle，AUV）问题中。文献[17]利用深度学习的栈式自编码模型对高光谱影像进行光谱特征提取，通过混合蛙跳算法对目标函数进行优化从而实现对最佳端元组合的搜索。文献[18]提出了一种混合蛙跳算法和禁忌搜索（shuffled frog leaping algorithm along with the tabu search，SFLA-TS）的算法。文献[19]引入变邻域搜索算法提升蛙跳算法的局部搜索能力，引入针对关键工厂的全解空间禁忌搜索，扩大了算法解空间。文献[20]设计求解多约束车辆路径模型的改进混合蛙跳算法，改进聚类算法并结合邻近矩阵构造初始青蛙种群，设计自内而外的交流演化模式，定义远离矩阵，对青蛙进行引导性邻域搜索。文献[21]提出了采用单种群蛙跳优化的卷积神经网络算法对眼底多种病变进行检测。

本文提出一种核中心驱动混合蛙跳算法（shuffled frog leaping algorithm driven by nuclear center，NCSFLA），对容量限制车辆路径优化问题进行研究，提出一种核中心驱动混合蛙跳算法的容量限制车辆路径优化算法（shuffled frog leaping algorithm driven by nuclear center for capacity-limited vehicle routing problem，NCSFLA-CVRP），以提高容量限制车辆路径的优化性能。

1 基础概念

1.1 车辆路径问题的数学描述

单目标最优化问题一般分为最大值优化问题和最小值优化问题。本文采用容量限制车辆路径问题作为研究的对象，该问题属于单目标最小值优化问题，其定义及描述如式（1）所示。

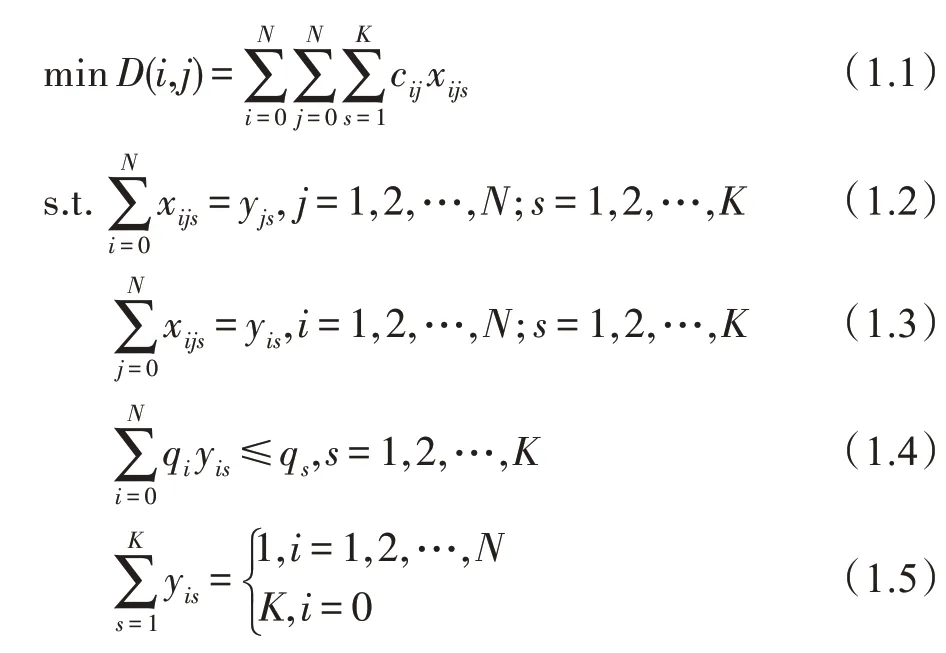
式中，(,)代表所有车辆的总路径长度，c代表客户和客户之间的运输距离，q代表客户的运输需求，q代表车辆的载荷容量，是客户的总数量，其中,=1,2,…,代表客户编号，=0 和=0 代表配送中心的编号，是车辆的总数量，其中=1,2,…,代表车辆编号，{x=1}代表车辆从客户到客户之间的有直接相连的路径，否则{x=0}，y和y分别代表客户和客户的需求由车辆满足。式（1.1）表示以配送中心0 开始编号的所有车辆的最小总路径长度，是待求解的目标函数。式（1.2）～（1.5）表示约束条件。式（1.2）～（1.3）表示车辆到达客户或客户后，又从该客户出发。式（1.4）表示每条配送线路上总客户需求量≤该配送线路上车辆的运载能力。式（1.5）表示每个客户仅和一辆车相关联，配送中心0 编号可以与辆车关联。

1.2 核中心驱动混合蛙跳算法

本文引入量子力学理论，以及玻尔原子模型理论，将SFLA 算法中的青蛙个体跳跃进化行为定义为量子力学行为，对原始混合蛙跳算法进行改进，提出一种核中心驱动混合蛙跳算法（NCSFLA）。

（电子轨道）将初始化的青蛙群体空间定义为量子空间，量子空间中有一个原子模型，多个青蛙可以看作这个原子模型中的多个电子以及一个由全局最优个体代表的原子核。青蛙的族群定义为多个电子轨道。则量子空间表示为：

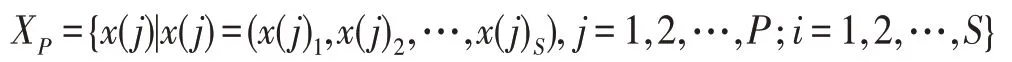
其中，量子空间中具有=×个青蛙初始个体，为族群个数，为族群内青蛙个数，青蛙个体分量()的维数记为。设各族群迭代局部进化次数为，全局进化次数为。

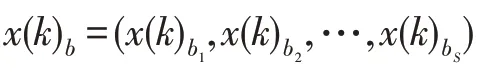
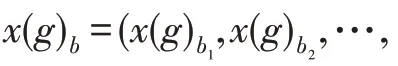
（个体跃迁步长）族群中个体跃迁步长定义为电子轨道中心与当前族群中最差个体的差值，记为_=()-()，()代表族群中最差个体。

（个体驱动步长）族群中个体驱动步长定义为原子核中心与当前族群中最差个体的差值，记为_=()-()，()代表族群中最差个体。

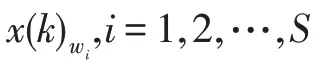
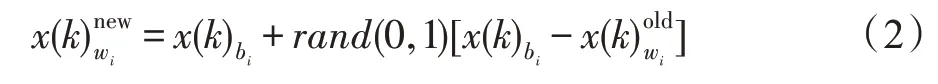
本文利用电子轨道中心驱动策略和原子核中心驱动策略对混合蛙跳算法中的一次局部进化进行改进，提出一种核中心驱动混合蛙跳算法。算法进化原理如图1 所示。

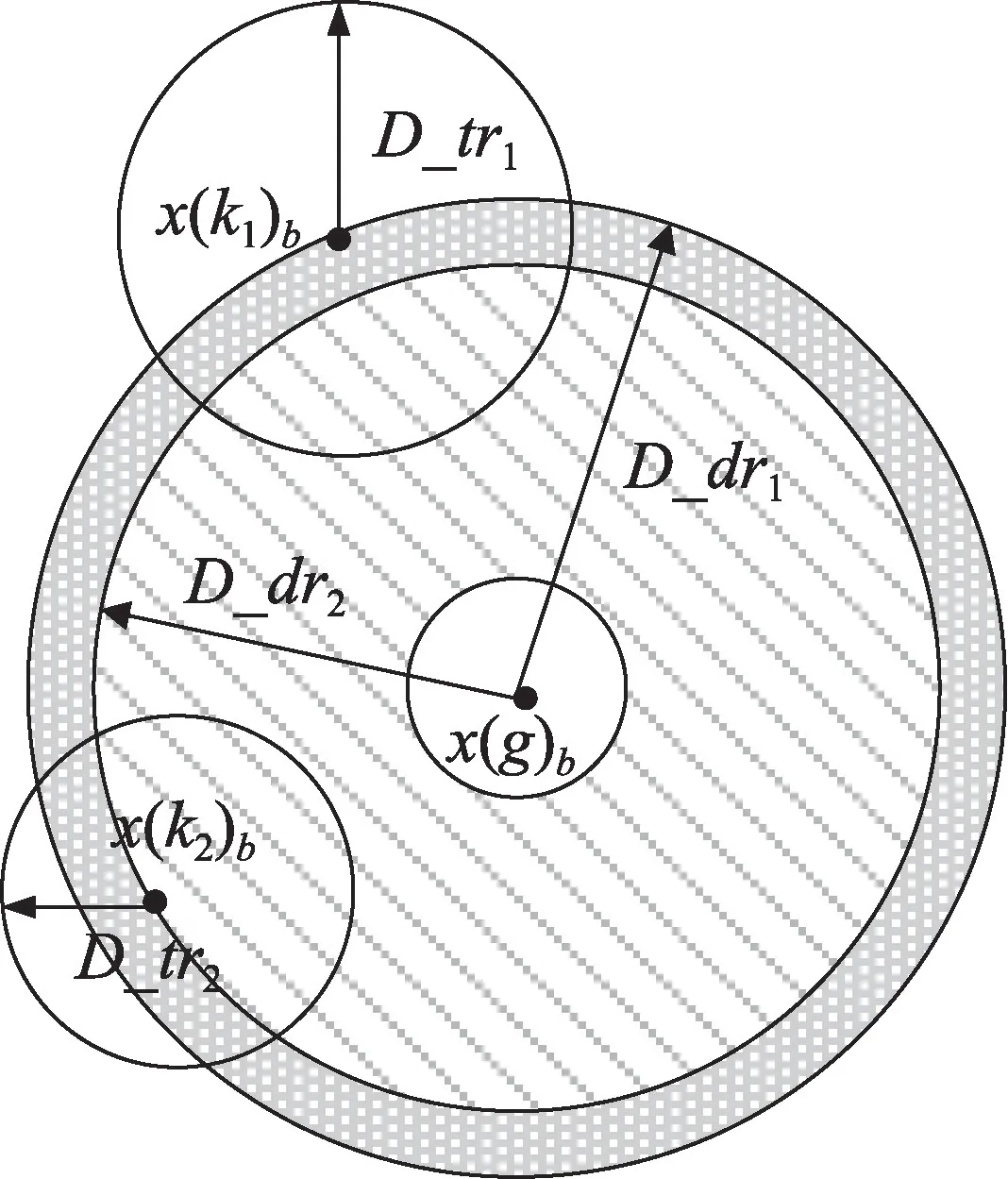
图1 核中心驱动混合蛙跳算法原理Fig.1 Principle of shuffled frog leaping algorithm driven by nuclear center

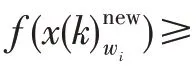
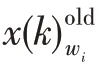
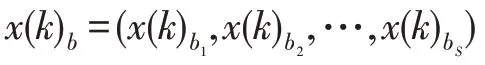
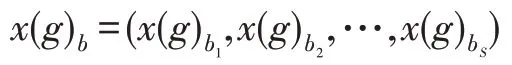
（3）若这个位置仍不够好，则丢弃该青蛙个体位置，使用式（4）随机产生不重复的青蛙个体分量。

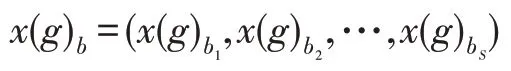
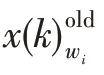
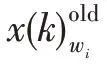
改进后的NCSFLA 算法收敛性能明显优于原始SFLA。

算法效率分析如下：SFLA的时间复杂度是(×××)，空间复杂度是(××)；NCSFLA的时间复杂度是(×××)，空间复杂度是(××)。可以看出，改进后的NCSFLA 算法与原始SFLA算法的时间复杂度和空间复杂度相同，其运算复杂度及运算成本与原始SFLA 相当。NCSFLA 实现时需要按照约定的概念进行电子轨道划分族群，并利用约定的概念进行族群内三种策略的改进，搜索策略中利用电子轨道中心、原子核中心为惯性指导，并且在进化更新时丢弃了跳跃步长的搜索范围限制条件，较易实现。

2 核中心驱动混合蛙跳算法的容量限制车辆路径优化算法

2.1 核中心驱动混合蛙跳算法的容量限制车辆路径优化问题

核中心驱动混合蛙跳算法的容量限制车辆路径优化问题可以看作单目标最小值优化问题，其数学描述可简化为式（5），其中目标函数是所有车辆路径总长。

假设青蛙个体分量()的维数为，=1,2,…,,=1,2,…,，则一个青蛙个体分量()代表路径优化编码里的每一个客户号，即一个青蛙个体是由位客户组成的，要求每个客户号是唯一的。安排车辆的方案主要依据客户编号排列次序及车辆最大装载量安排车辆，依次类推直到客户全部安排完毕为止。将客户的编码顺序解码为每个车辆的车辆路径序列。

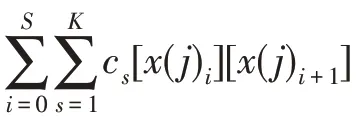
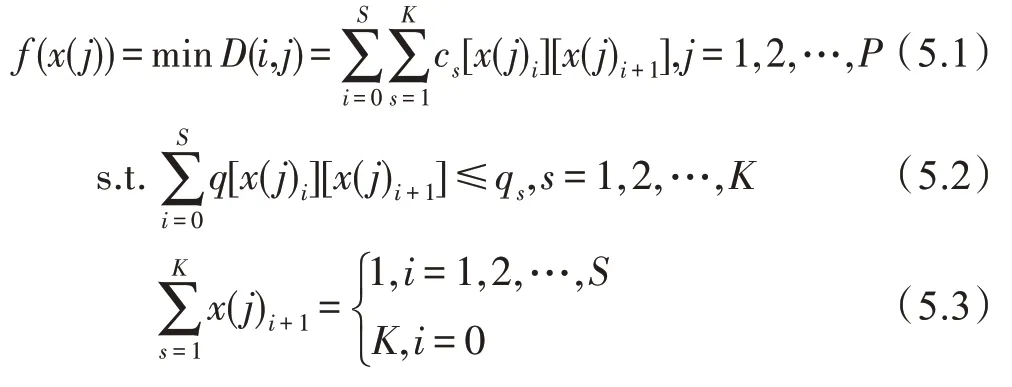
式（5.1）表示以配送中心0 开始编号的辆车总路径长度之和的最小值，这是单目标极小值最优化问题的目标函数。式（5.2）表示个客户的运输需求≤第辆车的载荷容量。因为=1,2,…,代表每个唯一的客户号，=0 代表配送中心的编号,第(=1,2,…,)辆车对应的那条路径总是从配送中心(=0)出发，再回到配送中心(=0)，所以式（5.2）涵盖了车辆到达客户或客户+1 后，又从该客户出发的约束条件，从而式（1.2）～（1.3）约束条件在此省略。式（5.3）表示每个客户仅和一辆车相关联，配送中心0 编号可以与辆车关联。

2.2 核中心驱动混合蛙跳算法的容量限制车辆路径优化算法流程

核中心驱动混合蛙跳算法的容量限制车辆路径优化算法

4.判断局部进化次数是否达到，若未达到，转至3；否则，判断青蛙族群全局进化次数是否达到或()是否达到收敛精度。若未达到，转至2；否则，算法停止，输出(())及优化路径序列。

2.3 算法流程图

核中心驱动混合蛙跳算法的容量限制车辆路径优化算法流程如图2 所示。

2.4 算法效率分析

NCSFLA-CVRP 的时间复杂度是(×××××)，空间复杂度是(×××+)。NCSFLACVRP 时间复杂度和空间复杂度会随着、和的变化而变化，视车辆路径数据规模而定。

3 实验

3.1 核中心驱动混合蛙跳算法性能测试实验

实验采用20 个测试函数分别对本文NCSFLA、带记忆功能的混合蛙跳算法（shuffled frog leaping algorithm with memory，MSFLA）、基于全局共享因子的混合蛙跳算法（shuffled frog leaping algorithm based on global sharing factor，GSFLA）、SFLA、和声搜索算法（harmony search algorithm，HSA）、人工蜂群算法（artificial bee colony algorithm，ABCA)进行优化性能测试实验。各测试函数表达式、搜索范围和理论极小值如表1 所示。最终测试结果采用独立运行30 次后的平均值。

表1 测试函数Table 1 Benchmark functions

实验参数设置如下：青蛙群体规模=200，族群数=20，族群内青蛙个数=10，青蛙个体维数=30，=10，=200。

六个算法对应的20 个测试函数收敛精度和速度比较如表2 所示，进化曲线如图3～图22 所示。从进化曲线可以看出，NCSFLA 算法进化收敛速度以及精度明显高于其他五种算法，尤其和是两个复合函数的情况下，本文算法也适用。表2 也显示了本文算法在单峰和多峰值函数的收敛精度上表现良好。

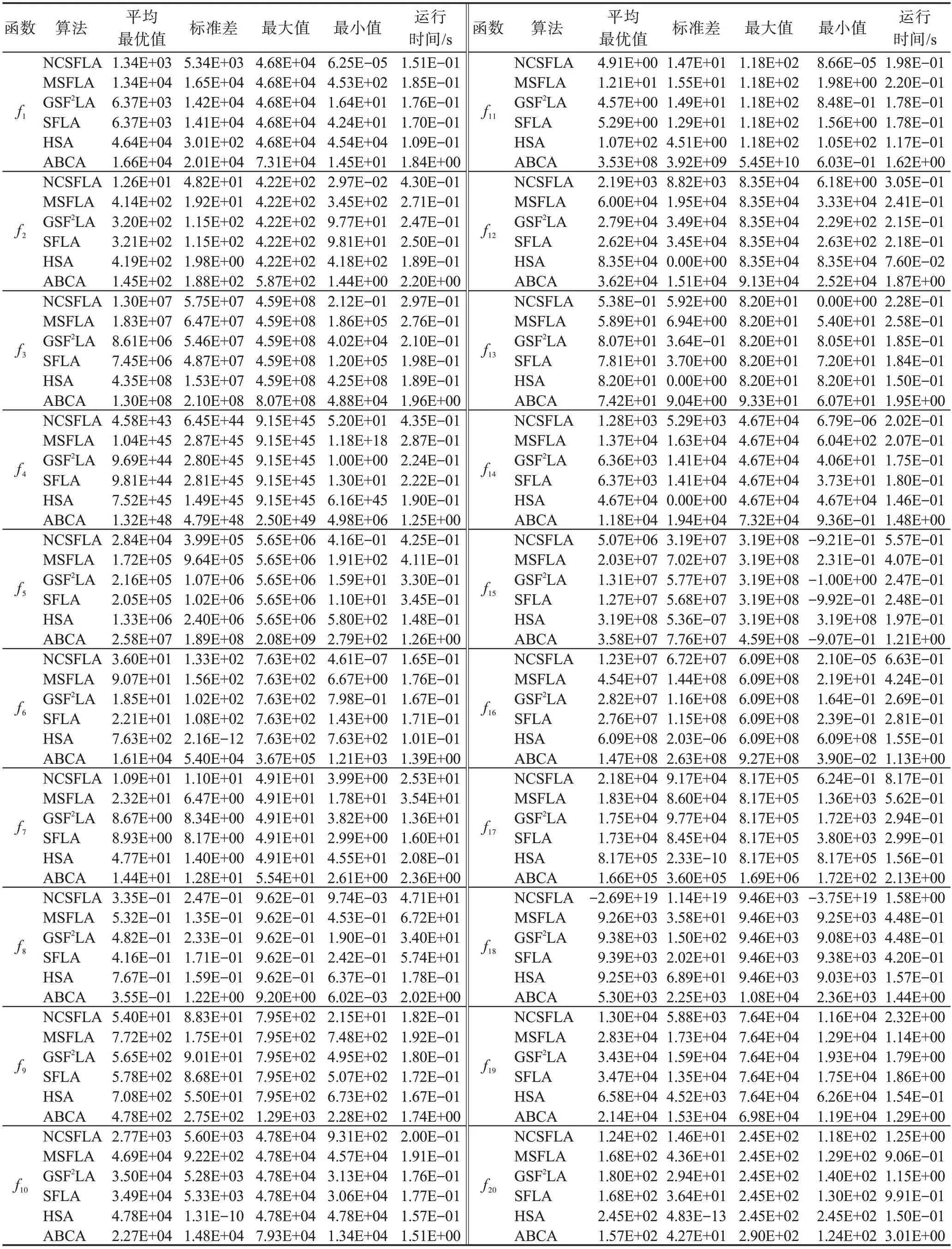
表2 收敛精度和速度比较Table 2 Comparison of convergence precision and convergence speed

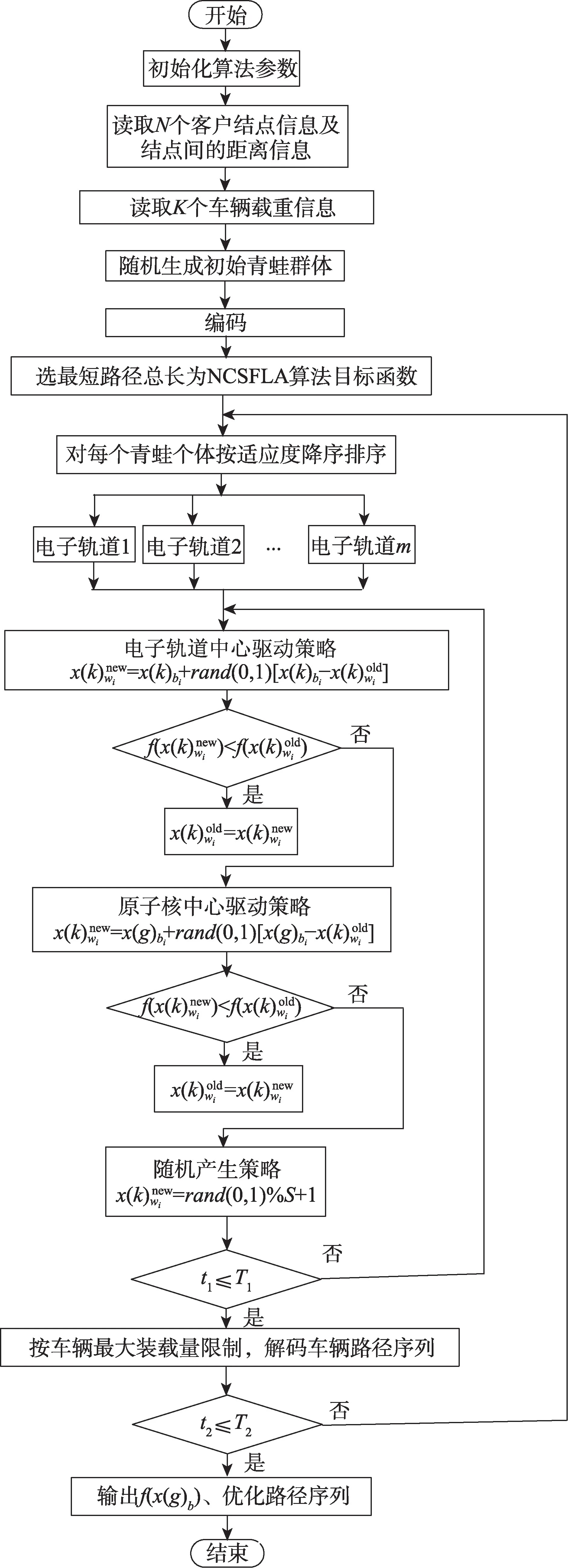
图2 改进的容量限制车辆路径优化算法流程Fig.2 Flow chart of improved capacity-limited vehicle routing problem

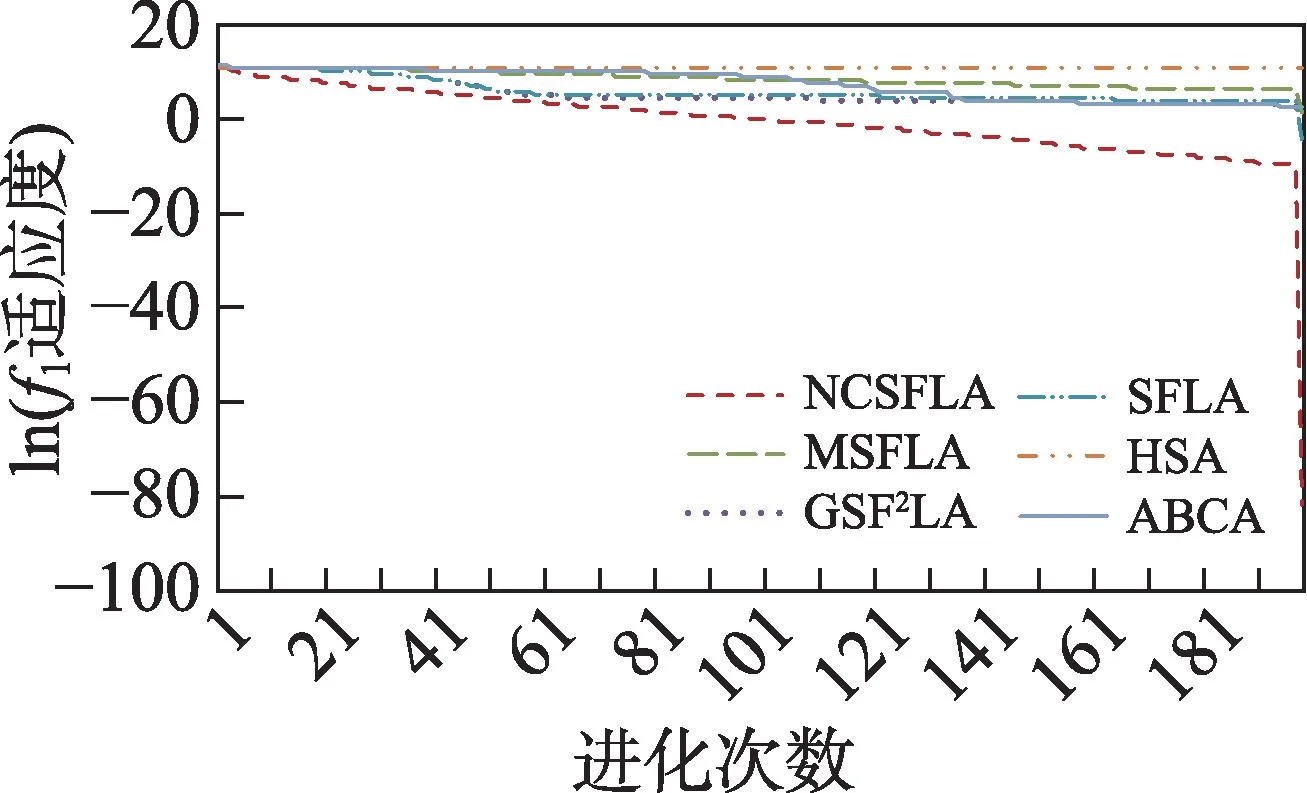
图3 f1进化曲线Fig.3 Evolution curves of f1

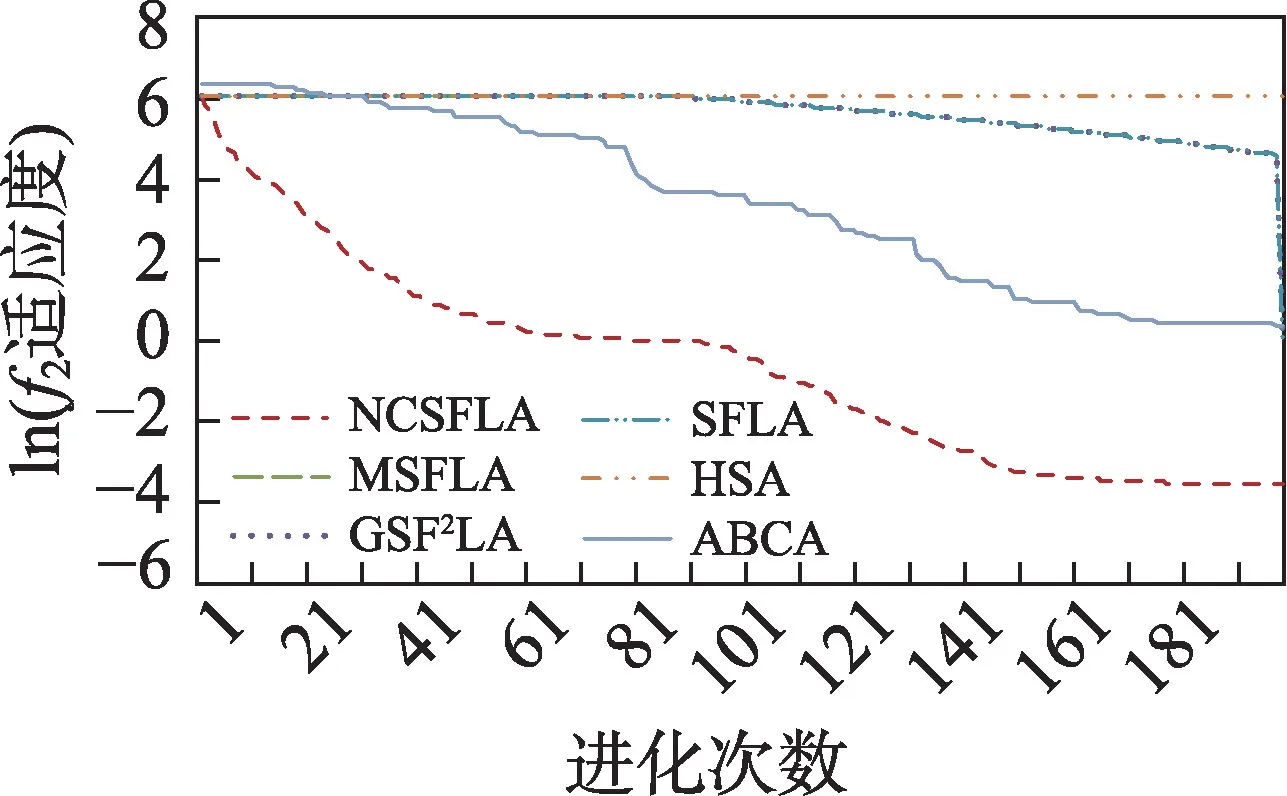
图4 f2进化曲线Fig.4 Evolution curves of f2

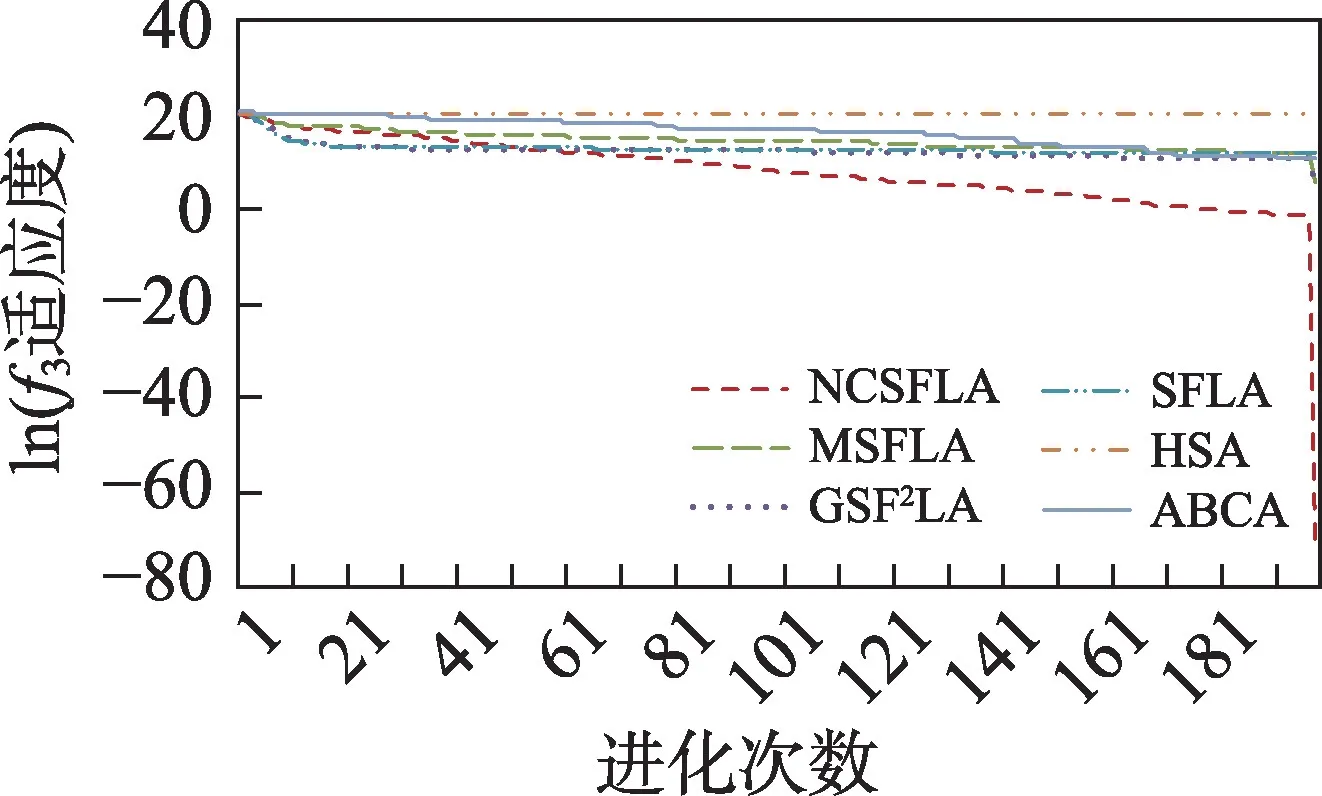
图5 f3进化曲线Fig.5 Evolution curves of f3

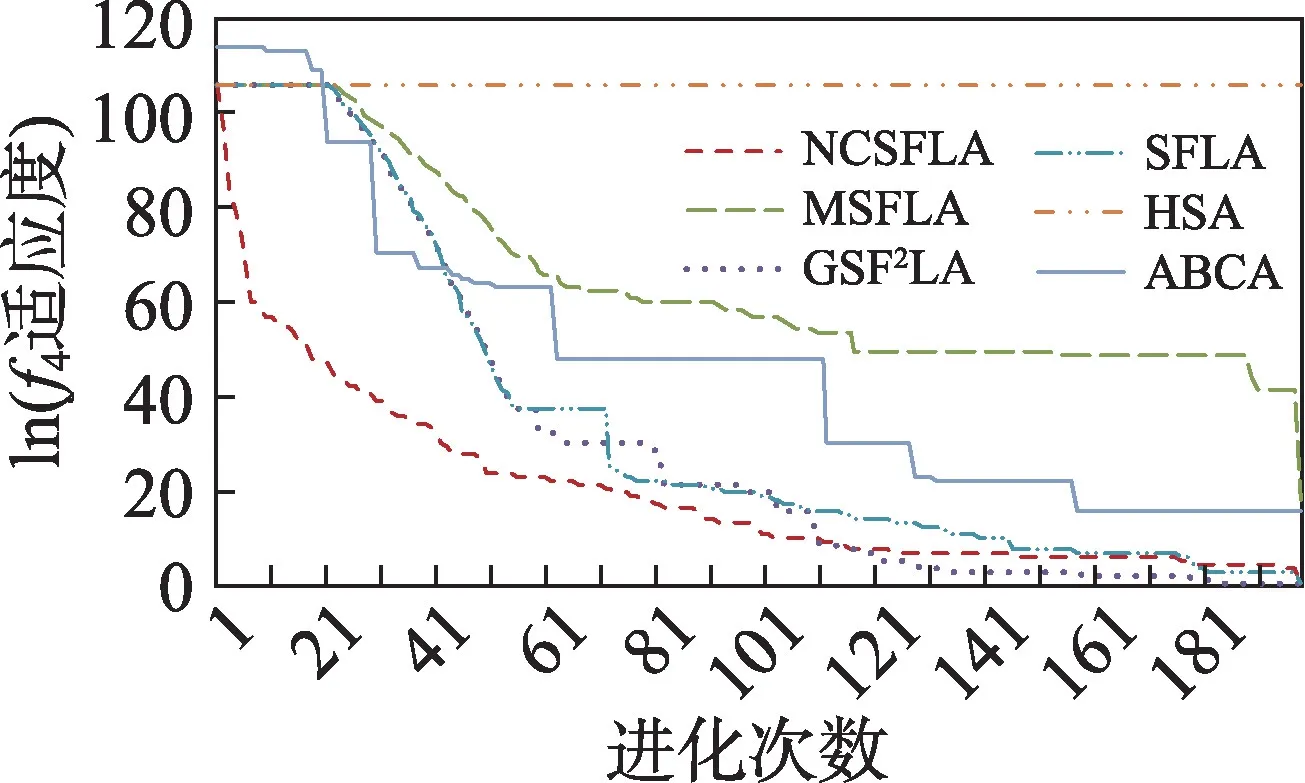
图6 f4进化曲线Fig.6 Evolution curves of f4

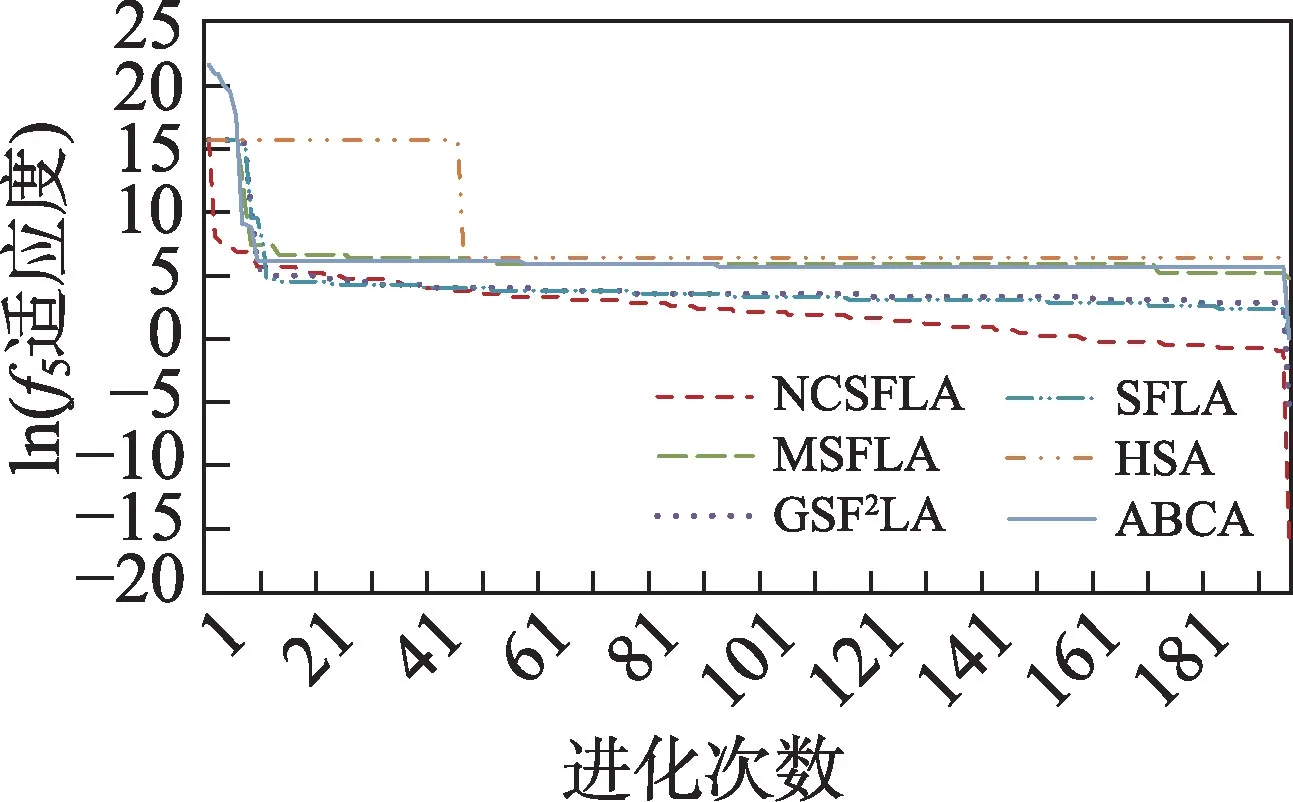
图7 f5进化曲线Fig.7 Evolution curves of f5

图8 f6进化曲线Fig.8 Evolution curves of f6

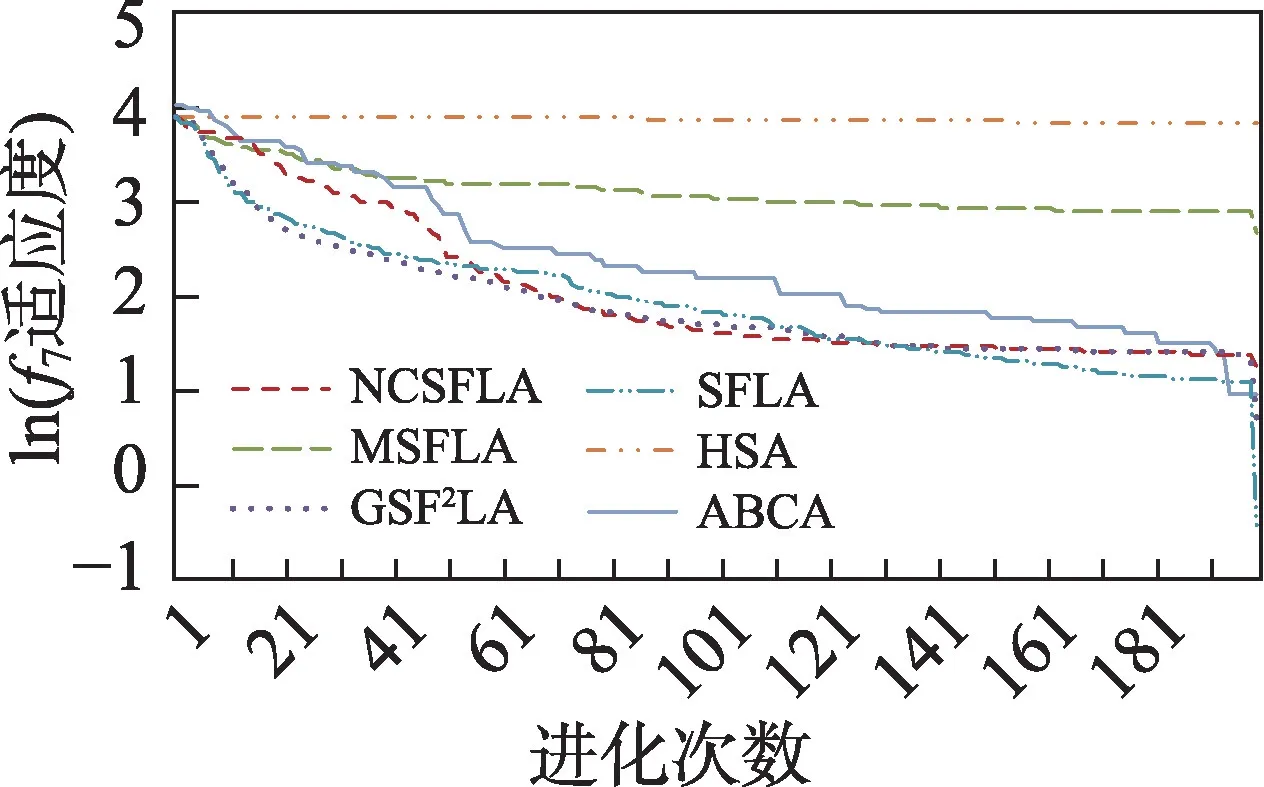
图9 f7进化曲线Fig.9 Evolution curves of f7

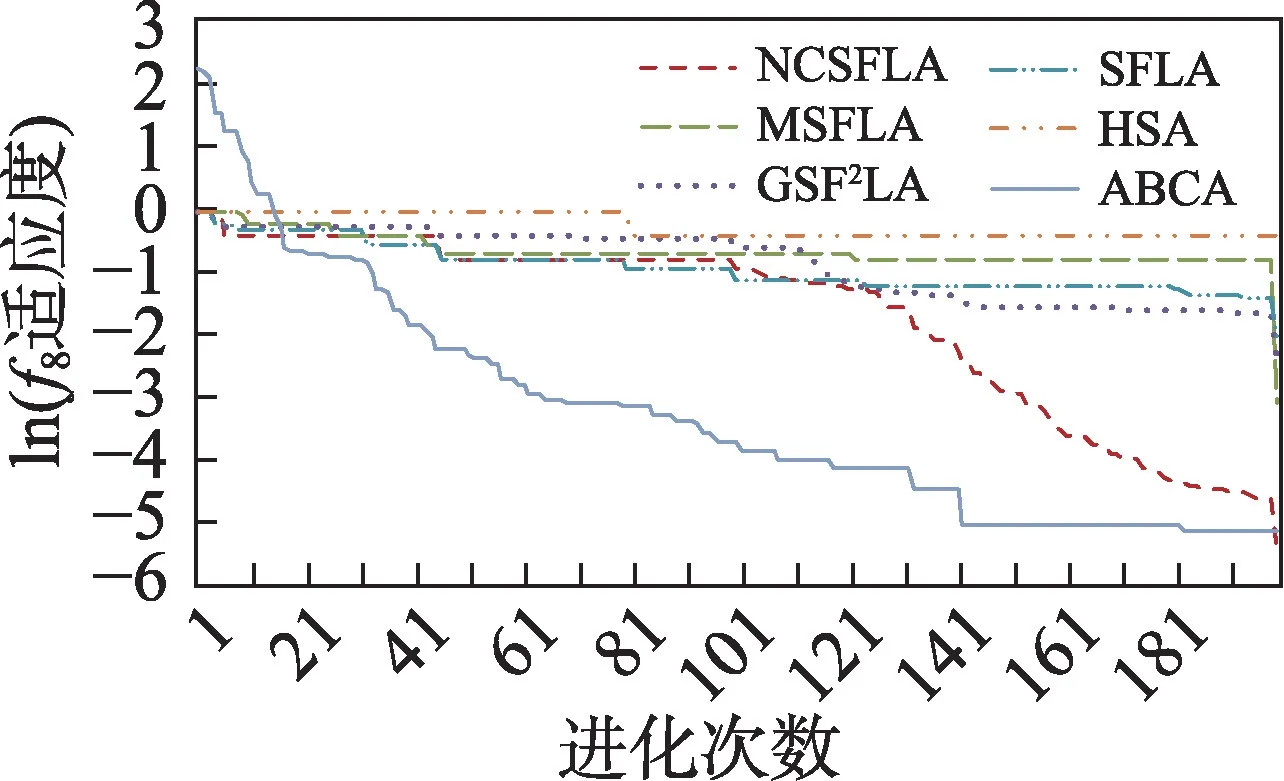
图10 f8进化曲线Fig.10 Evolution curves of f8

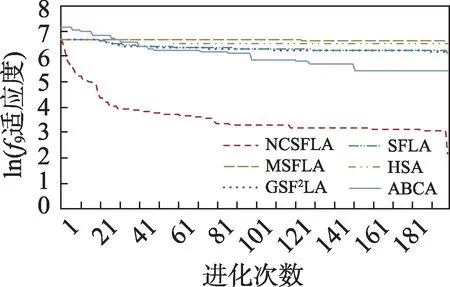
图11 f9进化曲线Fig.11 Evolution curves of f9

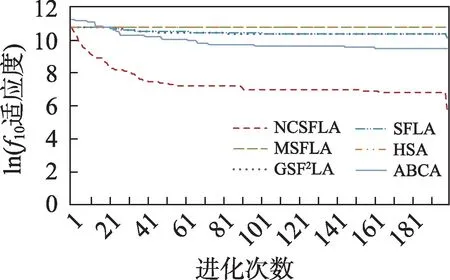
图12 f10进化曲线Fig.12 Evolution curves of f10

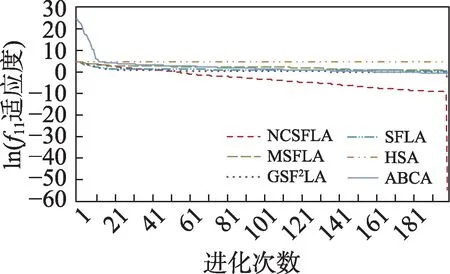
图13 f11进化曲线Fig.13 Evolution curves of f11

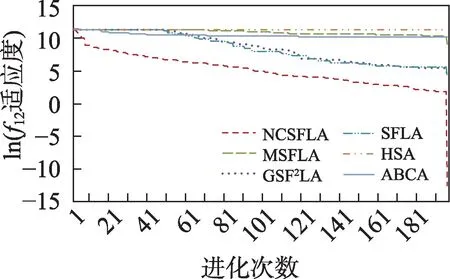
图14 f12进化曲线Fig.14 Evolution curves of f12

结果显示，针对20 个测试函数，本文提出的NCSFLA 算法相对于MSFLA、GSFLA、SFLA、HSA、ABCA 五种算法，具有收敛速度快、收敛精度高的特点，克服了原始SFLA 的缺陷。

3.2 核中心驱动混合蛙跳算法的容量限制车辆路径优化算法性能测试实验

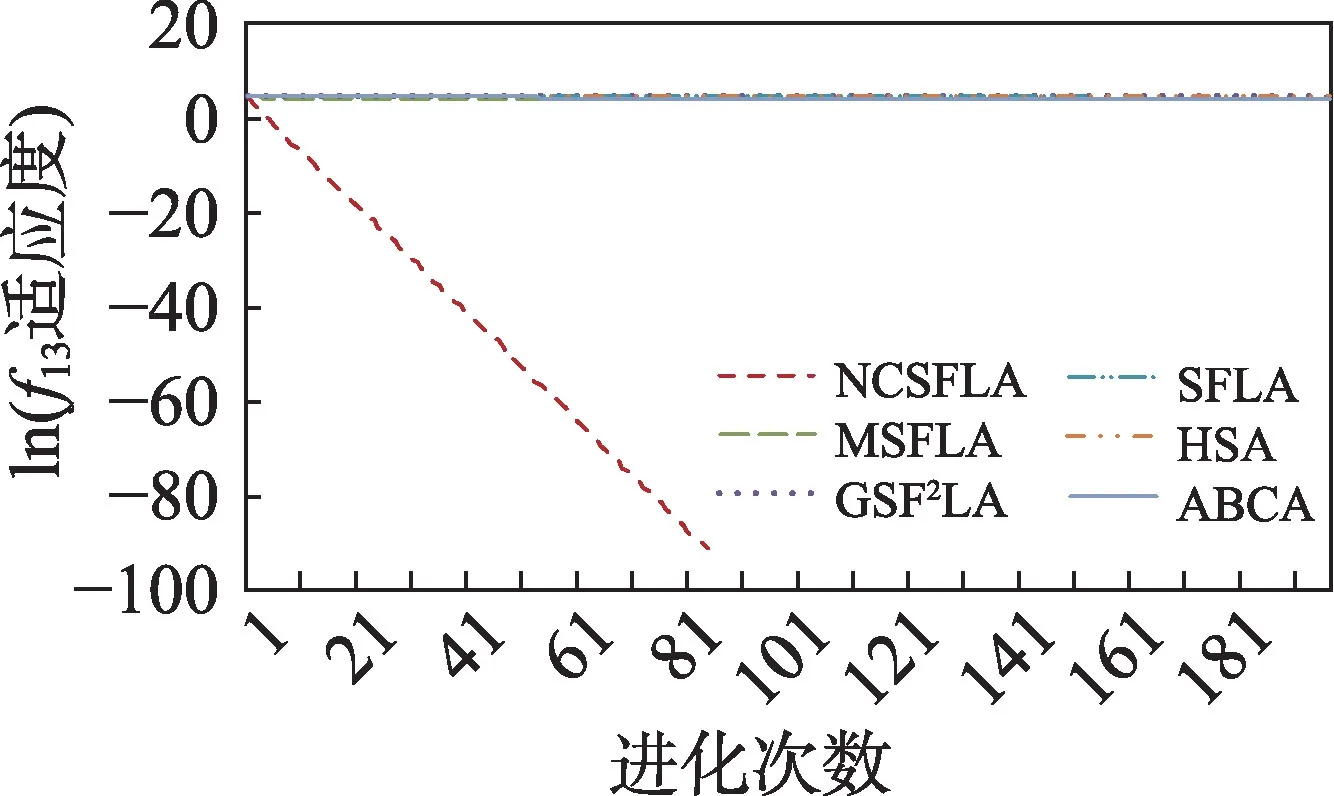
图15 f13进化曲线Fig.15 Evolution curves of f13

图16 f14进化曲线Fig.16 Evolution curves of f14

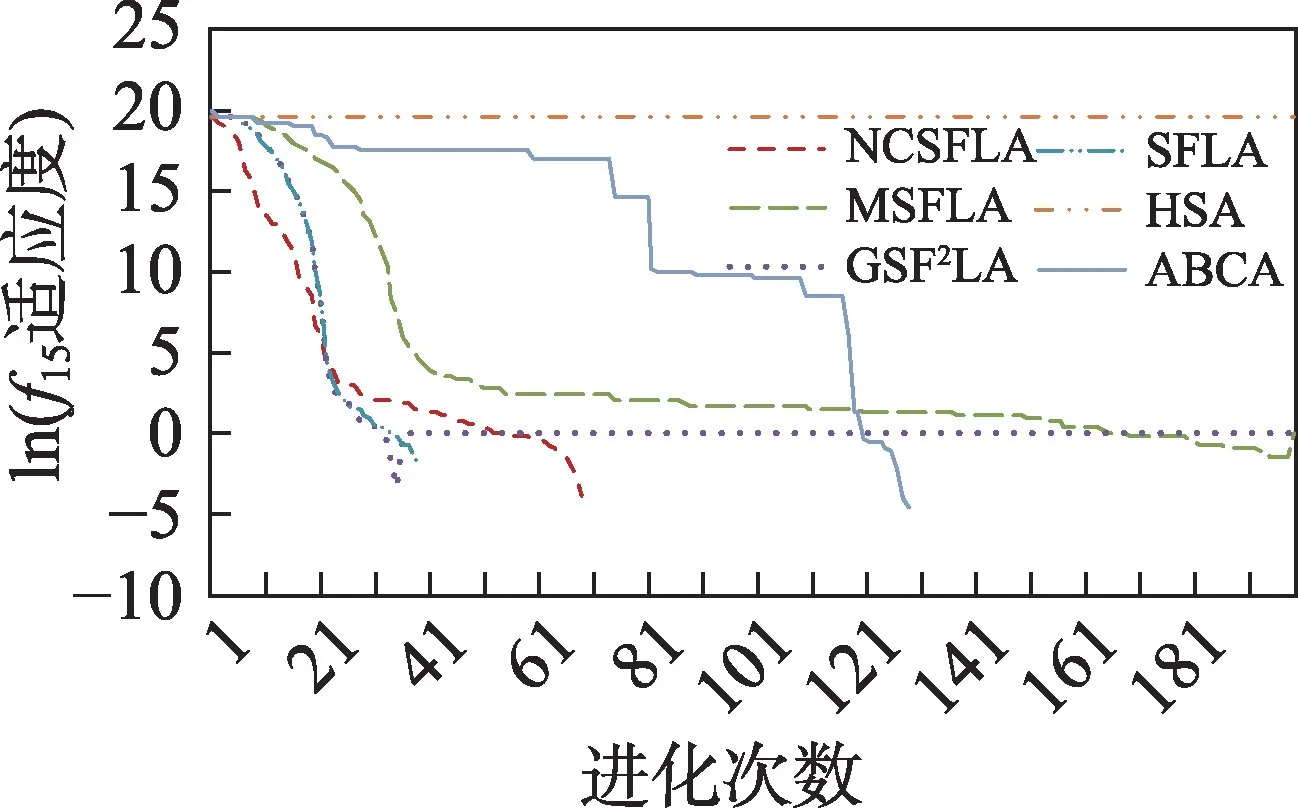
图17 f15进化曲线Fig.17 Evolution curves of f15

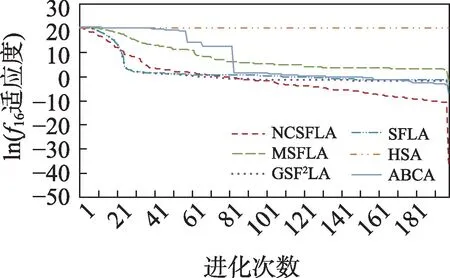
图18 f16进化曲线Fig.18 Evolution curves of f16

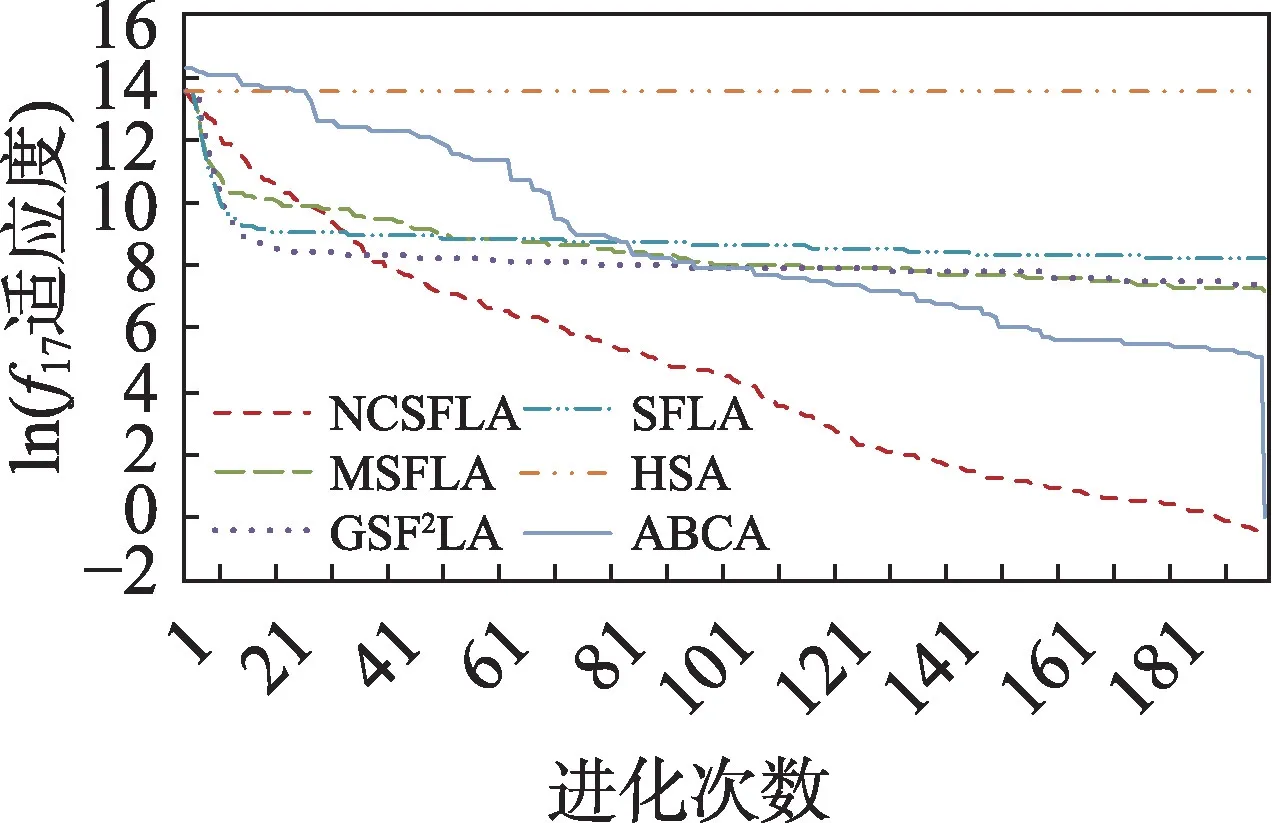
图19 f17进化曲线Fig.19 Evolution curves of f17

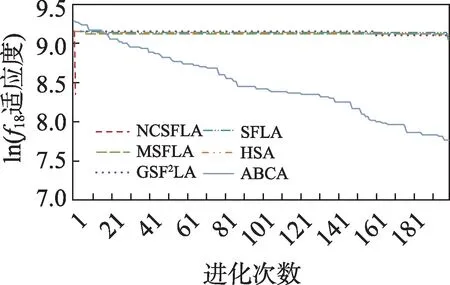
图20 f18进化曲线Fig.20 Evolution curves of f18

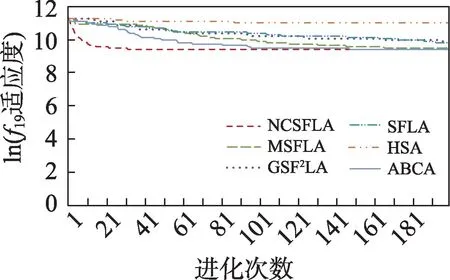
图21 f19进化曲线Fig.21 Evolution curves of f19

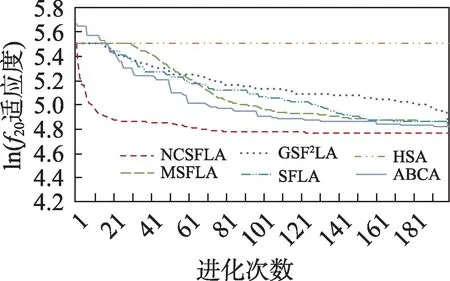
图22 f20进化曲线Fig.22 Evolution curves of f20

依据本文提出的NCSFLA-CVRP 算法解决容量限制车辆路径问题的思路，对上述其中三个算法MSFLA、GSFLA、SFLA进行修改，分别得到带记忆功能混合蛙跳算法的容量限制车辆路径优化算法（shuffled frog leaping algorithm with memory for capacity-limited vehicle routing problem，MSFLA-CVRP），基于全局共享因子混合蛙跳算法的容量限制车辆路径优化算法（shuffled frog leaping algorithm based on global sharing factor for capacity-limited vehicle routing problem，GSFLA-CVRP），基本混合蛙跳算法的容量限制车辆路径优化算法（shuffled frog leaping algorithm for capacity-limited vehicle routing problem，SFLACVRP）。实验采用这四种算法，采用Solomon算例（http://web.cba.neu.edu/～msolomon/problems.htm）标准测试数据中RC101 数据集对容量限制车辆路径问题进行优化性能测试实验。选取RC101数据集作为测试集。

实验参数设置如下：青蛙群体规模=200，族群数=20，族群内青蛙个数=10，青蛙个体维数=8，=10，=30 。客户结点个数=100，即青蛙个体维数=100，其中1～100 代表每个唯一的客户号，0 代表配送中心的编号。按照车辆数=2，=4分别进行测试，每辆车的车容量q=200。=2 时，各算法进化曲线如图23 所示，各算法车辆路径优化比较如表3 所示。=4 时，各算法进化曲线如图24所示，各算法车辆路径优化比较如表4 所示。

表3 各算法K=2 Solomon算例数据车辆路径优化比较Table 3 Comparison of vehicle routing optimization algorithms for Solomon example data while K=2

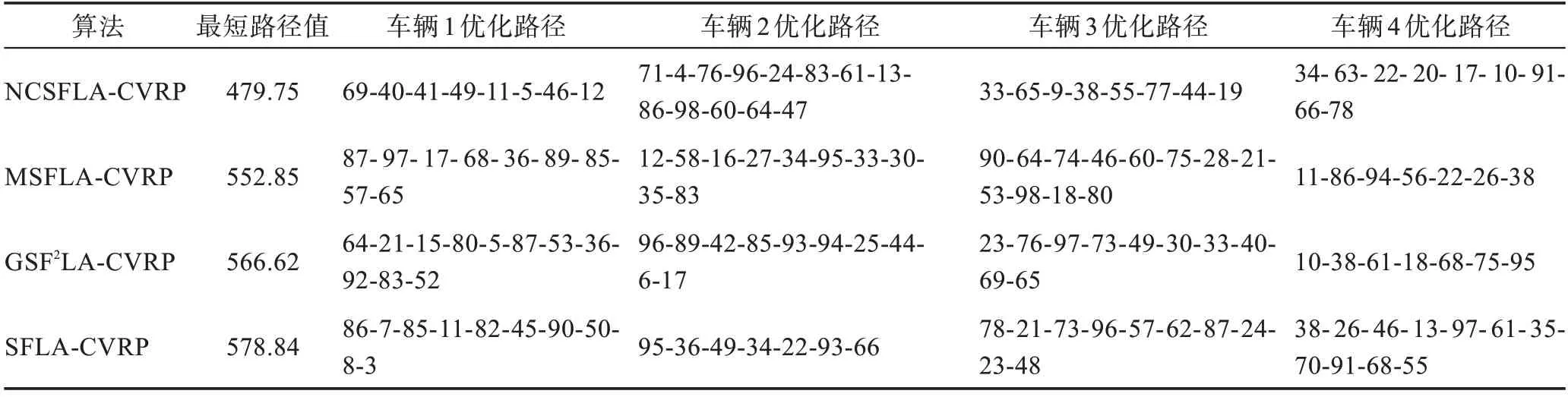
表4 各算法K=4 Solomon 算例数据车辆路径优化比较Table 4 Comparison of vehicle routing optimization algorithms for Solomon example data while K=4

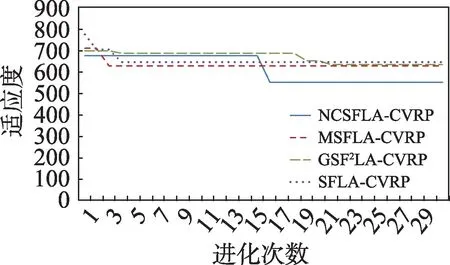
图23 各算法K=2 Solomon 算例数据进化曲线Fig.23 Evolution curves of each algorithm for Solomon example data while K=2

图24 各算法K=4 Solomon 算例数据进化曲线Fig.24 Evolution curves of each algorithm for Solomon example data while K=4

从以上测试结果可以看出，对标准测试数据RC101 数据集，NCSFLA-CVRP 算法在不同车辆数情况下均体现出较优的最短路径值。算法进化曲线也显示出在固定进化次数条件下，NCSFLA-CVRP 算法具有较为平稳的进化曲线，使得它不易陷入早熟收敛。在多车辆测试中，随着车辆数的增多，车辆优化的路径更加满足客户的实际需求。以上结果表明，NCSFLA-CVRP算法较MSFLA-CVRP、GSFLA-CVRP、SFLA-CVRP 三种算法具有更高的效率和可靠性，可以有效提高容量限制车辆路径的优化性能。

由于CVRP 问题属于NP 难解问题，很难在多项式时间复杂度范围内求得最优解。本文将提出的核中心驱动混合蛙跳算法应用于解决该问题，提出NCSFLA-CVRP 算法，以青蛙个体分量代表路径优化编码里的每一个唯一的客户号，将客户的编码顺序解码为每个车辆的车辆路径序列，并以配送中心0开始编号的辆车总路径长度之和的最小值作为算法的适应度目标函数，在约束满足的条件下将CVRP问题简化为求解单目标极小值最优化问题。算例结果表明，本文提出的NCSFLA-CVRP 算法具有快速收敛的效果，提高了算法的执行效率，取得了较优的最短路径值。同时，算法具有较高的鲁棒性和可靠性，在多车辆条件下仍可满足多客户的实际需求。

4 结束语

本文引入量子力学理论以及玻尔原子模型理论，将SFLA 算法中的青蛙个体跳跃进化行为定义为量子力学行为，对原始混合蛙跳算法进行改进，提出一种核中心驱动混合蛙跳算法。将该算法应用于容量限制车辆路径优化问题，提出了一种核中心驱动混合蛙跳算法的容量限制车辆路径优化算法。实验结果显示单峰值、多峰值函数以及复合函数等20 个测试函数，NCSFLA 算法相对于MSFLA、GSFLA、SFLA、HSA、ABCA 五种算法具有收敛速度快、精度高的特点，克服了原始SFLA 的缺陷。Solomon 算例标准测试数据实验结果表明NCSFLA-CVRP 算法较MSFLA-CVRP、GSFLA-CVRP、SFLA-CVRP 三种算法具有更高的效率和可靠性，有效提高了容量限制车辆路径的优化性能。