面向稀疏数据的协同过滤用户相似度计算研究

武 森，董雅贤，魏桂英，高晓楠

北京科技大学 经济管理学院，北京100083

互联网和信息技术的普及与应用，使得海量信息不断产生与传播，信息过载成为普遍关心的问题。推荐系统因其能有效过滤信息，满足用户个性化服务的需求，在视频、音乐、电子商务等领域起到关键作用。协同过滤是一种重要和应用广泛的推荐算法，其基本假设是用户兴趣具有延续性，即若过去两用户的偏好相似，则未来其偏好也具有相似性。协同过滤首先计算用户或项目间相似度，在此基础上，预测目标用户对目标项目的评分并进行有效推荐，因此合理的相似度计算成为实现精准推荐的关键。

随着用户数目与项目数量的增加，用户-项目评分矩阵稀疏程度加剧，例如，公开数据集MovieLenslatest-small 仅具有一个或两个共同评分项的用户对数目达到19%。传统数值相似度计算方法如皮尔逊相关系数（Pearson correlation coefficient，PCC）、余弦相似度（cosine similarity，COS）、修正余弦相似度（adjusted cosine similarity，ACOS）等首先查找共同评分项，进而由共同评分项评分数值计算相似度。稀疏数据中共同评分项的减少将导致传统数值相似度度量方法难以准确计算用户或项目间的相似度，因此推荐效果随之降低。与数值相似度不同，结构相似度依据用户是否曾对项目进行评分这一行为计算相似度，主要度量两用户评分项是否相关。杰卡德相似度（Jaccard）为常用的结构相似度计算方法，衡量用户共同评分项占比，计算简单，但由于其完全忽视评分数值，获得的结构相似度区分度低，难以辨别不同用户之间相似性的差异。综合相似度[通过融合结构相似度与数值相似度综合用户评分的结构信息与数值信息，可同时衡量用户评分相关性与偏好一致性，改善数值相似度在稀疏数据中受共同评分项稀少影响难以准确计算相似度的问题。然而现有综合相似度大多依托于Jaccard，因此未能彻底解决区分度较弱的不足，且未能有效避免稀疏数据中数值相似度影响综合相似度准确性，相似度计算可靠性有待提升。

针对稀疏数据难以准确计算相似度的问题，本文提出稀疏余弦相似度（sparse cosine similarity，SCS）提高稀疏数据中用户相似度计算准确性。稀疏余弦相似度首先定义稀疏集合相似度（sparse set similarity，SSS）以度量稀疏数据中的用户结构相似度。稀疏集合相似度通过结合数值度量，增强区分度以优化结构相似度计算。进一步，设置稀疏集合相似度阈值，针对稀疏集合相似度大于阈值的高相关用户与不满足阈值要求的低相关用户，分别定义数值相似度计算方法，降低数值相似度对评分稀疏用户综合相似度的影响，以规避数据稀疏时对数值相似度的误导。最终，稀疏余弦相似度利用稀疏集合相似度阈值与调整系数平衡结构相似度与数值相似度贡献，克服传统数值相似度计算方法由于依赖共同评分项，在稀疏数据中计算准确性受到较大影响的问题，且改善原有结构相似度区分度弱的问题。

1 相关工作

协同过滤因其不用考虑推荐项目的内容、技术易于实现等优点被广泛使用。随着用户、项目数量的剧增，用户-项目评分矩阵的稀疏性导致协同过滤推荐的准确性降低。针对这种情况，学者提出多种解决方法，其中包括数据填充、降维以及新相似度计算方法。

数据填充即针对缺失评分进行填补，利用平均数、中位数等可实现填补，但这种方法将所有缺失的评分填补为相同的值，与实际情况不符。还有学者将聚类等方法应用于数据填充，如对用户进行聚类，将簇内用户评分均值用于数据填充，然而数据稀疏将影响聚类效果，进而影响用户评分填充效果。

矩阵分解是经典的降维方法，可分为奇异值分解（singular value decomposition，SVD）、概率矩阵分解（probabilistic matrix factorization，PMF）、非负矩阵分解（nonnegative matrix factorization，NMF）等。针对用户-项目评分矩阵的分解，NMF 的纯加性具有更好的解释性，因此成为推荐领域最受欢迎的降维工具之一。矩阵分解将用户-项目评分矩阵分解为低维矩阵，降低计算数据的维度，但可能导致信息丢失。

相似度计算方法将直接影响协同过滤推荐效果，作为实现有效推荐的关键步骤，受到学者广泛研究。为解决数据稀疏问题，新相似度计算方法层出不穷。其中，一部分学者在相似度计算过程中融入更多信息，通过丰富信息量来增强稀疏数据中相似度的可靠度。如提取用户隐含评分、上下文信息、用户年龄、教育水平、用户兴趣主题等用于用户相似度计算。然而这些信息的可获取性将影响这类相似度计算方法的适用性。另有许多学者则针对稀疏的评分数据设计新相似度计算方法以提高用户相似度计算准确度，可分为数值相似度、结构相似度、综合相似度。

1.1 数值相似度

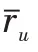
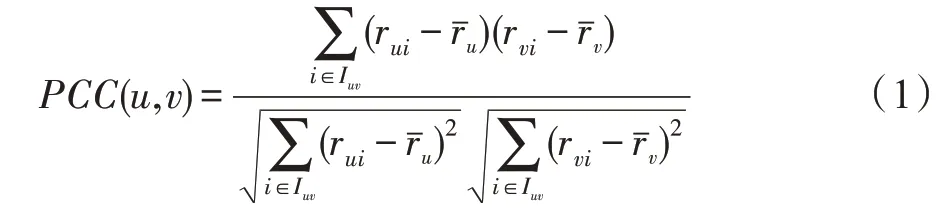
COS将用户评分视为向量，将两个评分向量之间的角度的余弦值用作相似度值，如式（2）所示。

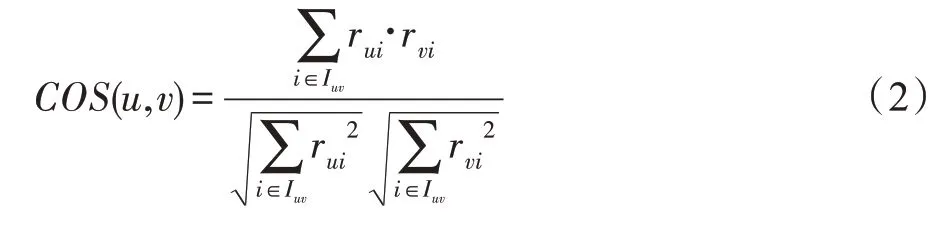
但是，COS 未考虑不同用户的评级偏好，ACOS则针对这一问题进行了改进，如式（3）所示。

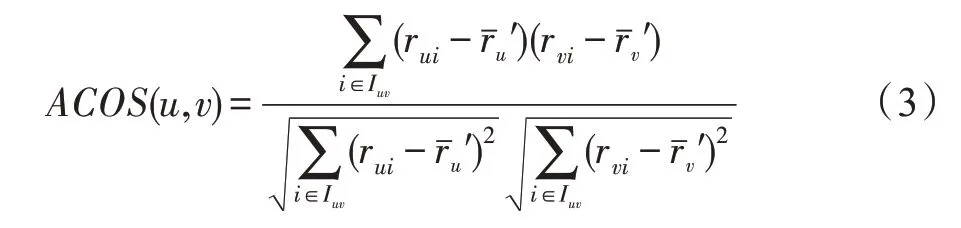
PCC、COS、ACOS 都属于对称相似度，即、之间的相互影响力相同。有学者认为用户间相互影响力存在差异，并提出不对称余弦相似度。

上述传统的数值相似度计算依赖用户对共同评分项的评分数值，具有以下缺点：首先，仅使用共同评分项评分数值，未使用非共同评分项评分数值，信息利用不充分；其次，共同评分项稀少时无法准确计算相似度。然而在实际推荐场景中，用户项目评分矩阵稀疏，用户间共同评分项稀少影响相似度计算准确性进而影响推荐效果。以算例分析稀疏数据对用户相似度计算的影响。

假设用户集合{,,,,}对各项目的评分如表1 所示。

表1 用户-项目评分矩阵算例Table 1 Example of user-item rating matrix

针对表1 中部分用户的评分进行详细分析，结果如表2 所示。以(,)表示用户、间的相似度。{,}共同评分项数、共同评分项所占比例均大于{,}，且{,}共同评分项评分差距较小，因此(,)应大于(,)。同理，(,)应大于(,)。针对表1计算用户相似度，部分结果如表3所示。

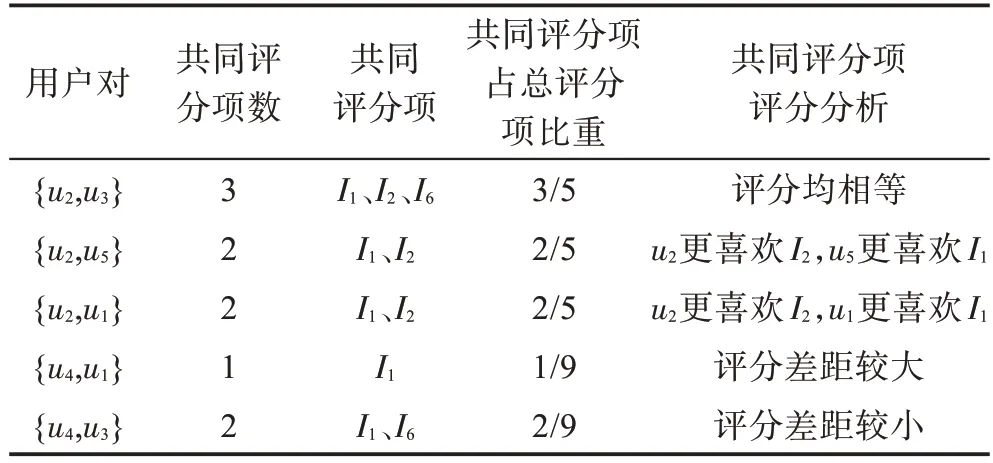
表2 部分用户评分分析Table 2 Analysis of partial user ratings

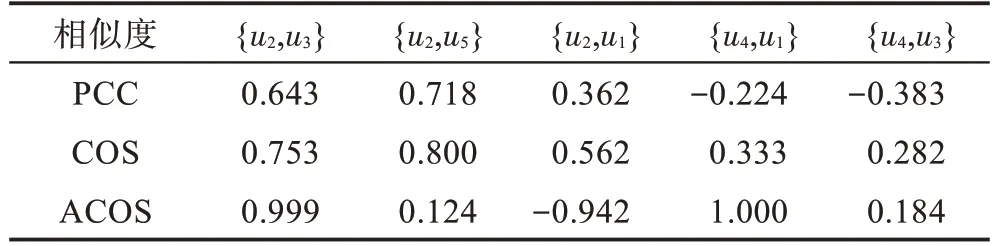
表3 部分用户相似度计算结果Table 3 Similarity measure of partial users

表3 中，PCC(,)小于PCC(,)，COS(,)小于COS(,)，COS(,)小于COS(,)，ACOS(,)小于ACOS(,)。对比表2 分析结果与表3计算结果，数据稀疏时受共同评分项数稀少影响，数值相似度计算结果不合理。

1.2 结构相似度

结构相似度根据用户是否曾对项目进行评分计算相似度，其受数据稀疏影响较小，但不考虑具体评分数值，易损失信息。Jaccard 是经典的结构相似度，可以找到倾向于共同评价的高度相关的用户，但未考虑评分数值，无法判断用户偏好的一致性且区分度较弱。如，表1 中{,}与{,}共同评分项评分差距不同，因此(,)应不同于(,)，然而Jaccard(,)=Jaccard(,)=0.4。

1.3 综合相似度

综合相似度结合数值相似度与结构相似度，往往可弥补这两类相似度的缺点，提高稀疏数据用户相似度计算准确性。Bobadilla 等提出了一种综合相似度度量方法，该方法结合Jaccard 和数值相似度MSD（mean squared differences），称为JMSD（Jaccard mean squared differences）。Liu 等提出数值相似度PSS（proximity significance singularity），并结合改进的Jaccard 形成综合相似度NHSM（new heuristic similarity model）以提高稀疏数据中用户相似度计算准确性。Wang 等利用KL 散度（Kullback Leibler divergence）改进PSS，以共同评分项占比计算结构相似度，最终形成的综合相似度适用于稀疏数据用户相似度计算。Patra 等提出一种结合Jaccard 和巴氏系数的综合相似度计算方法，称为BCF（Bhattacharyya coefficient in collaborative filtering）。巴氏系数利用用户所有评分信息克服共同评分的限制，有助于计算稀疏数据中用户数值相似度。Bag 等提出噪声识别与较正的方法，与巴氏系数集成，针对无噪声稀疏数据展开推荐。Mu 等为了缓解稀疏问题引入海林格距离和Jaccard，以降低共同评分项稀少给相似度计算带来的影响。Bag 等认为目标用户单独评分项数与其他用户单独评分项数对用户相似度计算的作用不同并提出一种不对称的JMSD 称为RJMSD（relevant Jaccard mean square distance）。

综合相似度同时考虑用户评分结构与评分数值，受数据稀疏影响较小，然而未能有效避免共同评分项稀少时数值相似度误导。已有综合相似度研究通常利用调整系数调节结构相似度与数值相似度的权重来结合两种相似度计算结果。假设(,)与(,)分别表示用户、的结构相似度与数值相似度，则用户、的综合相似度(,)大多如式（4）所示。

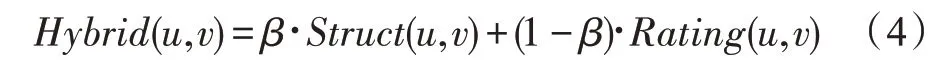
若以融合Jaccard 与ACOS 构成综合相似度。以表1 数据为例，经计算小于0.88 时，(,)大于(,)，显然不合理。而取值越大代表综合相似度涵盖的数值信息越少，即对用户偏好一致性的判断越弱。若为缓解共同评分项稀少时数值相似度的误导，将调整得过大，则会弱化共同评分项繁多时综合相似度判断偏好一致性的作用。因此，这类综合相似度难以有效避免数据稀疏时数值相似度的误导。

现有综合相似度主要借助用户共同评分项占比计算结构相似度，再进一步与数值相似度结合，未能有效提升结构相似度区分度，且受数据稀疏影响严重的数值相似度会影响综合相似度的计算结果。因此，提出一种新的综合相似度计算方法——SCS。SCS 首先定义融入数值信息的结构相似度计算方法SSS，增强结构相似度的区分度。相较于原有综合相似度仅依靠调整系数调节结构相似度与数值相似度权重，难以规避稀疏数据数值相似度极端值影响，SCS 利用阈值与调整系数实现综合相似度中结构相似度与数值相似度权重的双重调节，规避共同评分项稀少时数值相似度对综合相似度的误导，提高稀疏数据中用户相似度的准确性，提升推荐效果。

2 面向稀疏数据的协同过滤用户相似度SCS

2.1 融合数值信息的结构相似度SSS

为改进结构相似度区分度低的问题，首先新定义了集合聚合度和集合离差度，进而提出通过集合聚合度与集合离差度融合数值信息的结构相似度SSS，作为提出面向稀疏数据的协同过滤用户相似度SCS 的基础。

（集合聚合度（set aggregation，SA））假设用户集合包含||个对象，的集合聚合度()如式（5）所示。

其中，表示中所有用户评分项集合的交集的对象个数，即中用户共同评分项的个数，表示中所有用户评分相等的项目个数。以表1 为例，令={,}，则()=2×2+2×0=4。

集合聚合度从集合结构和数值两方面提炼集合内信息，统计集合结构的相似信息，统计集合内数值相等信息，且由于只针对共同评分项判断评分是否相等，因此，必小于等于。集合聚合度综合集合结构与数值信息，且结构信息对集合聚合度影响更大。

（集合离差度（set deviation，SD））假设表示由各项目评分的最大值组成的最大值向量，表示由各项目评分的最小值组成的最小值向量，的集合离差度()如式（6）所示。

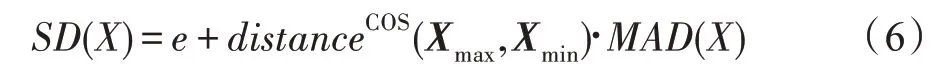
其中，表示中仅有部分用户进行评分的项目个数，如式（7）所示。

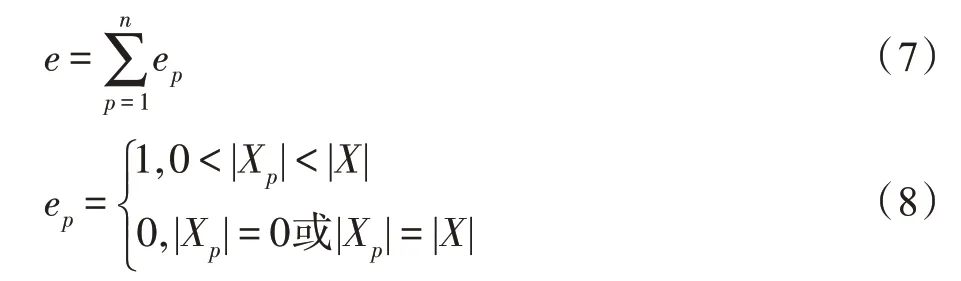
其中，各用户可对个项目进行评分，|X|表示中对项目进行评分的用户个数。

式（6）中，(,) 表示的最大值向量与最小值向量间的余弦距离，如式（9）所示。

式（6）中，()表示的平均绝对离差，如式（10）所示。

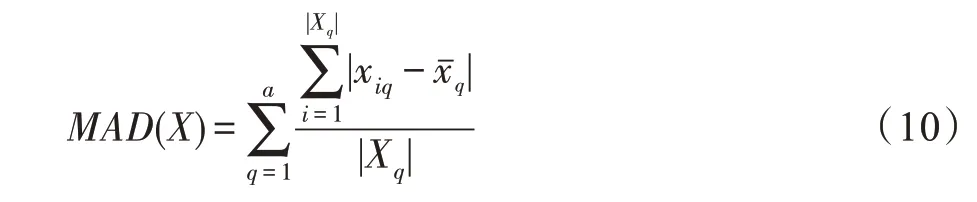
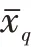
集合离差度从集合结构与数值两方面提炼集合内信息，描述集合结构的差异信息，()描述集合内数值差异，且由于数据稀疏，将缩小数值差异在集合离差度中的比重，使集合离差度将以结构差异信息主导。以表1 为例，令={,}，则()=3+0.030 5×2=3.061。

（稀疏集合相似度（SSS））假设()表示的集合聚合度，提炼集合结构相似与数值相等的信息。()表示的集合离差度，提炼集合结构差异与数值离散的信息。将()与()结合，的稀疏集合相似度()如式（11）所示。

以表1为例，令={,}，则()=1.307，={,}，则()=1.32。相比于Jaccard，稀疏集合相似度利用集合聚合度、集合离差度在考量评分结构的同时增加了数值度量，有效提升区分度。集合聚合度只针对共同评分项判断评分是否相等，结构信息对集合聚合度影响更大；集合离差度利用集合最大值与最小值的余弦距离缩小评分数值信息在其计算中的比重。因此综合集合聚合度与集合离差度的稀疏集合相似度仍以度量评分结构为主的同时，又因增加了数值度量而较Jaccard 更具有区分度。

2.2 SSS 与数值相似度进一步结合的SCS

当={,}时，()表示用户、的稀疏集合相似度，此时稀疏集合相似度侧重于计算两用户的结构相似度。结构相似度主要度量两用户评分项是否相关，难以判断两用户偏好是否一致。将稀疏集合相似度与数值相似度进一步结合则可同时实现对相关性与偏好一致性的衡量。然而针对稀疏数据，数值相似度计算不灵敏，其相似度计算结果常产生误导。例如，假设用户、用户、用户的评分向量分别是（5，—，—，1，—）、（3，1，—，—，—）与（5，—，2，—，4）（“—”表示未进行评分），此时(,)=(,)=(,)=1，(,)=(,)=(,)=1，然而用户、对第一项的偏好存在较大差异，而用户、对第一项的偏好是相似的，显然在稀疏数据中传统数值相似度COS 与ACOS 计算结果与实际情况不相符。特别地，若目标用户与其他用户皆仅存在一个共同评分项，依据COS 则目标用户与其他用户相似度皆为1，表现为高度相似，此时数值相似度产生误导。现有综合相似度大多如式（4）所示，利用调整系数融合结构相似度与数值相似度，其准确性受数值相似度准确性与结构相似度准确性共同影响，未能有效避免共同评分项稀少时数值相似度误导。

稀疏集合相似度取值受共同评分项占比影响，因此进一步设置稀疏集合相似度阈值，借助衡量用户相关性的稀疏集合相似度将用户区分为高相关用户与低相关用户。若稀疏集合相似度高于阈值，即用户评分结构存在较大相关性，称为高相关用户，此时用户间共同评分项所占比例较大，数值相似度可有效衡量偏好一致性；若稀疏集合相似度低于阈值，即用户评分结构相关性较低，称为低相关用户，此时用户间共同评分项所占比例较小，共同评分项相对较少，数值相似度计算结果更易产生误导，因此针对不同用户的数值相似度采用差异化处理，更有助于综合衡量用户相似度。基于上述思想提出稀疏余弦相似度SCS。

（稀疏余弦相似度（SCS））假设(,)表示用户、的稀疏集合相似度，用户、的稀疏余弦相似度(,)如式（12）所示。

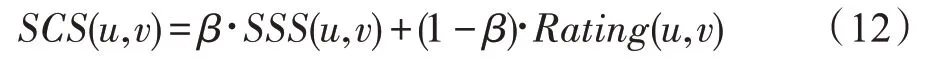
其中，(,)表示用户、的数值相似度，如式（13）所示。

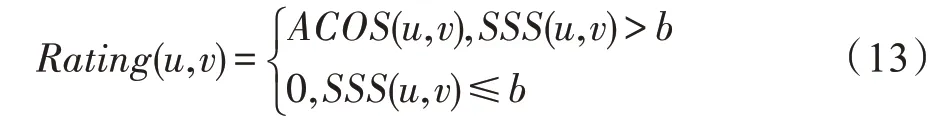
以表1 为例，若令SCS 阈值为0.5，则用户为用户的低相关用户，用户为用户的高相关用户，此时若令调整系数为0.5，则(,)为0.124，(,)为0.377，即用户与用户更为相似，与表1 中用户数据特征一致。

SSS 可衡量用户评分的结构相似度，ACOS 则常用于计算两用户评分的数值相似度。由于ACOS 受数据稀疏影响较大，共同评分项较多、占比较高时，ACOS 计算结果较为准确，而共同评分项较少、占比较低时计算结果更易产生误导。因此，针对共同评分项繁密的高相关用户，引入调整系数平衡结构相似度与数值相似度比重，同时衡量评分相关性与偏好一致性；由于共同评分项稀疏的低相关用户的数值相似度更易产生误导，故而仅以结构相似度计算综合相似度，避免数值相似度对用户相似度产生误导。

简言之，稀疏余弦相似度首先提出综合考虑数值信息与结构信息的稀疏集合相似度，增强了结构相似度区分度；进而，设置稀疏集合相似度阈值区分高相关用户与低相关用户，针对不同用户定义差异化的数值相似度计算方法；最终，稀疏余弦相似度利用阈值与调整系数双层调节稀疏集合相似度与数值相似度，可有效度量稀疏数据中用户相似度。

2.3 SCS 时间复杂度、空间复杂度分析

假设推荐系统中含有个用户、个商品，在构建用户相似度矩阵时需分别计算用户两两间相似度，因此基础的时间复杂度为()，利用稀疏余弦相似度构建用户相似度矩阵的时间复杂度同样为()，与COS、Jaccard、ACOS 一致，未增加时间复杂度。而空间复杂度主要来源于存储用户相似度矩阵，利用稀疏余弦相似度构建的用户相似度矩阵的空间复杂度为()，与COS、Jaccard、ACOS一致，未增加空间复杂度。

3 实验与结果分析

3.1 数据集

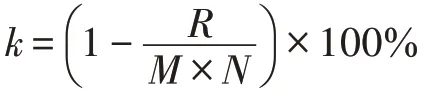
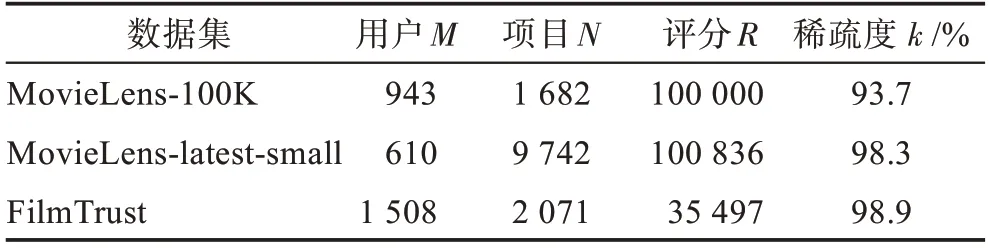
表4 数据集描述Table 4 Description of datasets

实验采用随机划分的方式将80%的数据作为训练集，20%的数据作为测试集。实验中取5 次实验的算术平均值作为最终结果。

3.2 评价指标

采用平均绝对误差（mean absolute error，MAE）与均方根误差（root mean squared error，RMSE）作为衡量评分预测准确性的标准，二者反映协同过滤利用最近邻计算的预测评分与用户实际评分的贴近程度，值越小，表示基于所使用的相似度计算方法的协同过滤推荐性能越好。MAE 如式（14）所示，RMSE如式（15）所示。

其中，r表示用户U对项目I的实际评分；R表示相应的预测评分；表示测试集的样本数量。

3.3 各相似度效果对比

为验证SCS 有效性，采用6 种广泛应用的经典相似度计算方法以及1 种新颖不对称相似度RJMSD 与SCS 在不同数据集进行实验对比，选取当前目标用户不同最近邻数，进行多次实验，以排除偶然因素。实验中SCS 需要预先设置阈值，给定取值范围={0,0.1,0.2,…,1.0}，分别计算SCS 对应的预测精度，将MAE、RMSE 最小时阈值的值视为最优取值。实验结果如图1、图2 所示。对比实验用到的相似度计算方法见表5。

表5 对比方法描述Table 5 Description of comparison methods

图1 不同相似度MAE 对比Fig.1 Comparison of MAE with different similarities

图2 不同相似度RMSE 对比Fig.2 Comparison of RMSE with different similarities

在MovieLens-100K、MovieLens-latest-small 中，SCS 在MAE 与RMSE 两个指标均取得最优效果。在FilmTrust中，SCS 在MAE 指标取得最优结果，而针对RMSE 指标在=80、100 时，其表现不如COS，其余最近邻数下均取得最优效果，且针对RMSE 指标，COS、PCC、SCS、Jaccard 效果皆较为接近。综合三个数据集实验结果，原有相似度计算方法受数据稀疏影响较大，由稀疏数据计算相似度时计算结果易产生误导，而数据稀疏对SCS 计算效果影响较小，针对稀疏数据SCS 可以更准确地计算用户相似度，优于原有相似度计算方法。

此外，对比SCS 与利用降维解决稀疏问题常用的基于NMF 的推荐方法，由于NMF 不涉及最近邻数，对比两种方法在MAE 与RMSE 下的最优值与均值，如表6 所示。

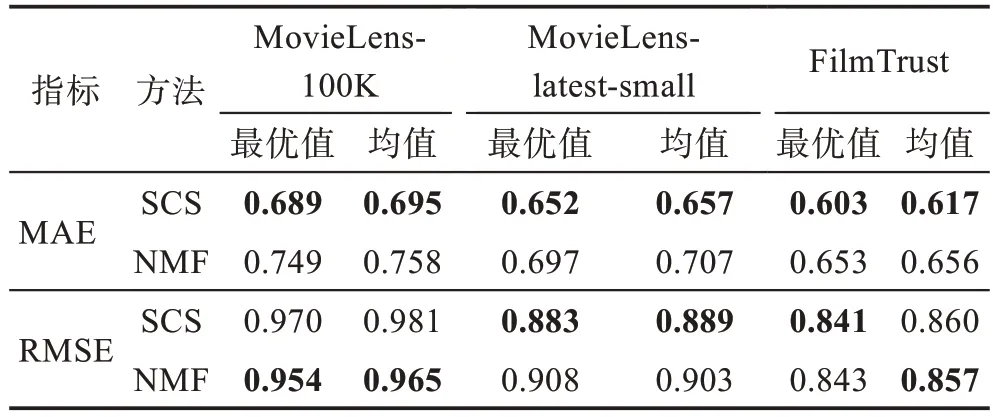
表6 SCS 与NMF 推荐效果对比Table 6 Recommended performance comparison of SCS and NMF

针对MAE 指标，SCS 在三个数据集中均明显优于NMF，MAE 平均降低0.05。针对RMSE 指标，在MovieLens-latest-small数据集中，SCS效果优于NMF，RMSE 平均降低0.02；在MovieLens-100K 数据集中，SCS 效果不及NMF，RMSE 平均提升0.02；在FilmTrust数据集中，SCS 与NMF 效果分别在最优值与均值取得最佳结果且差异较小。整体来看，SCS 优于NMF，可针对稀疏数据准确地进行推荐。

3.4 参数β 变化对SCS 推荐效果的影响

为了进一步说明SCS 推荐效果随参数的变化趋势，令阈值为0，选取当前目标用户不同最近邻数，比较不同数据集中取值变化对推荐效果的影响，实验结果如图3、图4 所示。

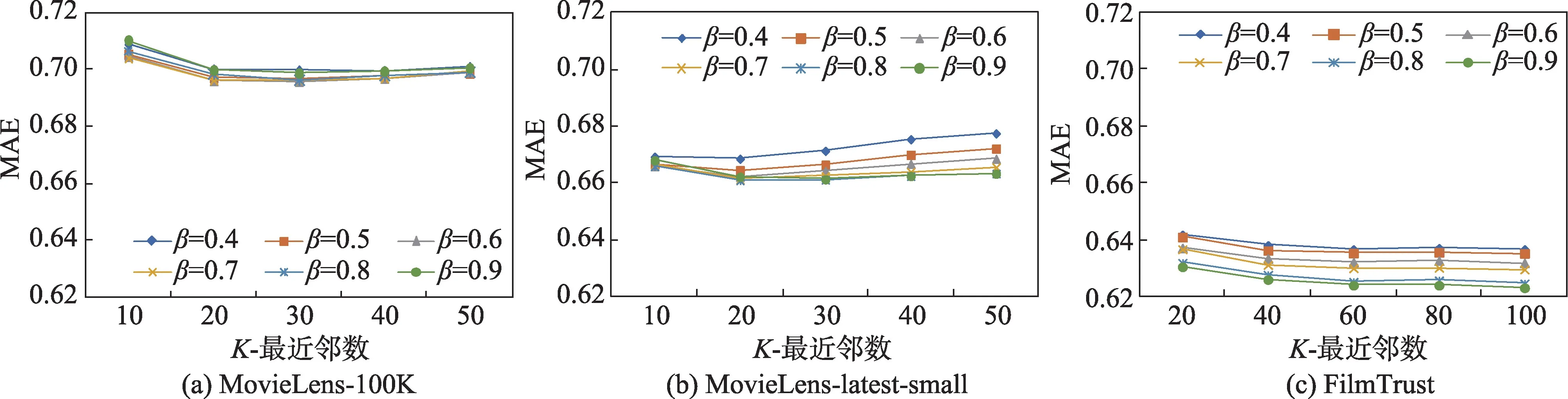
图3 β 的变化对稀疏余弦相似度MAE 的影响Fig.3 Influence of β on sparse cosine similarity MAE

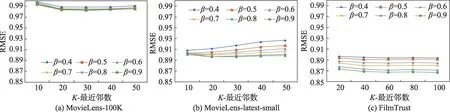
图4 β 的变化对稀疏余弦相似度RMSE 的影响Fig.4 Influence of β on sparse cosine similarity RMSE

在MovieLens-100K 中，取值范围在[0.6，0.8]时，易取得最优效果；在MovieLens-latest-small 中，取值范围在[0.7，0.8]时，易取得最优效果；在Film-Trust 中，取值范围为0.9 时，易取得最优效果。且随着变化，MAE 与RMSE 变化不明显，即较为稳健。在三个数据集中，随着稀疏程度提升，取得最优推荐效果的值也随之提升，且推荐效果随提升而提升的趋势越明显，即随数据稀疏程度提升，数值相似度产生较大误导，提高综合相似度中结构相似度占比并降低数值相似度影响有助于提升推荐效果。

3.5 参数b变化对SCS 推荐效果的影响

为了进一步说明SCS 推荐效果随参数的变化趋势，令取各数据集最优效果时取值，选取当前目标用户不同最近邻数，比较不同数据集中稀疏集合相似度阈值取值变化对推荐效果的影响，实验结果如图5、图6 所示。

图5 b 的变化对稀疏余弦相似度MAE 的影响Fig.5 Influence of b on sparse cosine similarity MAE

图6 b 的变化对稀疏余弦相似度RMSE 的影响Fig.6 Influence of b on sparse cosine similarity RMSE

在MovieLens-100K 中，取值范围在[0.2，0.3]时，易取得最优效果；在MovieLens-latest-small 中，取值为0.1 时，取得最优效果；在FilmTrust 中，取值为0.7 时取得最优效果。且随着变化，MAE 与RMSE 变化不明显，即取值对SCS 效果影响较小。由于SSS 取值必大于0，若令=0，即将全部用户视为高相关用户，与现有综合相似度计算方法相同；当＞0 时，阈值可将用户划分为高相关用户与低相关用户。在三个数据集中，通过增加稀疏集合相似度阈值，区分高相关用户与低相关用户相似度计算方法后，SCS 推荐效果均有所提升，且随着稀疏程度提升，增添稀疏集合相似度阈值对SCS 提升效果越强。

4 结束语

本文针对稀疏数据难以准确计算用户相似度，进而影响协同过滤推荐效果的问题，构造了稀疏余弦相似度。该方法首先通过融合用户评分结构信息与数值信息构造稀疏集合相似度，提高结构相似度区分度；接着，针对稀疏集合相似度设置阈值区分目标用户的高相关用户与低相关用户；然后，针对不同用户采用差异化的数值相似度计算方式；最后，综合结构和数值相似度形成稀疏余弦相似度，通过阈值与调整系数实现稀疏数据中相似度计算的双层调节，可有效度量评分稀疏时的用户相似度，提升推荐效果。本文采用MAE 与RMSE 指标来评价不同相似度计算方法的表现，在公开数据集MovieLens-100K、MovieLens-latest-small、FilmTrust 上的实验表明，相比已有相似度计算方法，稀疏余弦相似度受数据稀疏影响较小，可以更准确地计算稀疏数据中的用户相似度，提升推荐结果的准确率。