带有微孔黏弹性芯层的纤维金属混杂层合板振动分析模型
姜世杰,王子恒,于长帅,3,任旭辉,王昕彤,王相平,韩清凯,李 晖,
(1.东北大学 机械工程与自动化学院,沈阳 110819;2.东北大学 航空动力装备振动及控制教育部重点实验室,沈阳 110819;3.中国科学院 沈阳自动化所机器人学重点实验室,沈阳 110016;4.辽宁省航空发动机冲击动力学重点实验室,沈阳 110015)
纤维金属混杂层合板(fiber metal laminated plate, FMLP)被广泛用于航空航天领域[1-5]。然而,现阶段随着飞行器振动噪声问题越来越突出[6-8],FMLP已无法满足减振降噪的需求,为此国内外研究人员把目光投向了带有微孔黏弹性芯层(microporous-viscoelastic layers,MVL)的FMLP结构(简称为MVL-FMLP)。其由带有微孔结构的高分子黏弹性层与纤维树脂层交替铺设,并与金属外层粘接而成,具有质量轻、减振降噪能力强、抗疲劳性能突出、成本较低等一系列优点。
对于带微孔软芯层的不同层数、不同铺设形式的多种FMLP结构的振动特性研究,近年来国内外做了大量工作。赖余东[9]基于均一化思想建立了带蜂窝夹芯的复合材料板结构的有限元模型,并研究了蜂窝体胞尺寸参数对结构固有频率的影响。基于Reissner理论,任树伟等[10]提出了蜂窝夹芯层合板结构的自由振动与声振耦合理论模型,系统性地研究了芯层几何尺寸、层合板结构尺寸和声波入射方向等因素对结构的振动特性和隔声特性影响。Xiao等[11]建立了带有质量密度梯度放入泡沫芯层夹芯板的自由振动分析模型,并讨论了芯层材料参数对结构固有频率的影响。基于修正后的Gibson公式,邸馗等[12]研究了对边简支边界下,带有负泊松比的蜂窝夹层板板厚比、芯层厚度及胞元角度的改变对结构前4阶固有频率的影响。基于半解析法,Heshmati等[13]求解了弹性地基边界下带有功能梯度的多孔材料板结构的固有频率。Li等[14]分析了热环境下石墨烯增强的功能梯度多孔夹芯板结构的非线性振动响应。通过仿真与试验手段,Yurddaskal等[15]研究了曲率和泡沫密度参数对多孔泡沫夹芯板结构固有特性的影响规律。考虑压电效应和冯卡门大变形理论,Zeng等[16]建立了电负载下带有功能梯度多孔材料芯层的压电三明治板结构的非线性振动模型。基于非均匀电场模型,Zhu等[17]讨论了弹性地基等参数对带有多孔黏弹性芯层的锥形夹芯板非线性振动特性的影响。
综上,现有研究中很少关注带有二维规则分布微孔的黏弹性夹层结构。另外,上述研究较少关注并求解结构系统的振动响应与阻尼参数,无法全面评价该类型结构的振动特性。为填补该类型层合结构在动力学性能研究方面的缺失,本文考虑了上述影响,建立了带有微孔黏弹性芯层的FMLP结构振动分析模型。在设计并制备获得带有二维规则分布微孔的黏弹性材料的基础上,推导得出该类型材料的等效弹性模量,结合解析建模和试验测试,研究了微孔几何参数对层合结构固有频率、振动响应、阻尼性能的影响。本文所建立的理论模型可为该类型层合结构的优化设计与减振工程应用提供重要参考。
1 理论模型
1.1 模型描述
所研究的MVL-FMLP结构的理论模型如图1所示。以其中面作为参考平面,建立o-xyz坐标系。假设其长为a,宽为b,黏弹性层厚度为hv,纤维层厚度为hf,金属层厚度为hm。且假设纤维层由n层纤维布构成,各层纤维厚度相等,均为hf/n,纤维主轴方向与x轴的夹角为θ。同时,在微孔黏弹性层中,孔直径为d,沿x,y,z3个方向上的孔间距分别为p、q和m。此外,假设MVL-FMLP结构处于一端约束的悬臂边界条件,在R0(x0,y0)位置受到一个单点脉冲激励载荷f(t)的作用。
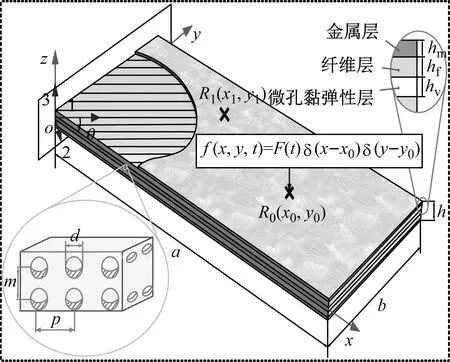
图1 MVL-FMLP结构理论模型
1.2 位移假设
根据经典层合板理论,纤维层与金属层的位移场如下
(1)
式中:u、v、w为板内任意一点位移;u0、v0、w0为中面位移;t为时间。
由于研究对象为对称结构,仅需考虑横向振动的影响。因此,纤维层与金属层内任一点的应变可表示为
(2)
式中,εx、εy和γxy分别为对应方向的正应变和切应变。
考虑到微孔黏弹性层中存在剪切变形[18-19],采用高阶剪切变形理论将MVL-FMLP结构中黏弹性层的位移场表示为
(3)
式中:Ψ=z-4z3/3h2;φx与φy分别为垂直于中面的直线在xoz面与yoz面内的转角。
微孔黏弹性层的应变可表示为
(4)
1.3 材料参数
根据文献[20],微孔黏弹性材料与构成孔壁材料的弹性模量之间有如下关系
(5)
式中:Ev、Gv、ρv分别为微孔黏弹性材料的杨氏模量、剪切模量与密度;Es、Gs、ρs分别为构成孔壁材料的相应参数。
将孔的几何参数d、p、q、m代入式(5),可导出二维规则微孔分布形式下黏弹层的弹性模量表达式为
(6)
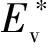
(7)
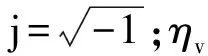
(8)
式中,ηm为金属层材料的损耗因子。
(9)
式中,ηfi、ηfk分别为纤维层对应方向的损耗因子。
1.4 应力-应变关系
对于MVL-FMLP结构,其各层材料的应力-应变关系式可描述为
(10)
在式(10)中,由于金属层材料与微孔黏弹性材料呈各向同性,因此有
式中:i=m,v;υi为泊松比。
对于具有各向异性特点的纤维层,有
式中,υ12和υ21分别为泊松比。
在纤维层中,当纤维主轴方向与设定坐标轴之间存在夹角θ时,根据应力-应变转轴公式[22]可得第k层纤维在设定坐标系内的应力-应变关系
(11)
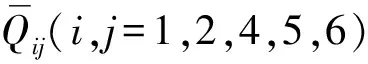
1.5 能量表达式
然后,可将金属层的动能Tm和应变能Um表示为
(12)
纤维层的动能Tf和应变能Uf可表示为
(13)
黏弹性层的动能Tv和应变能Uv可表示为
(14)
式中:Ni、ρi(i=m,f,v)分别为各层材料的总层数与密度;S为板面积。
MVL-FMLP结构总的动能T与应变能U的表示式如下
(15)
1.6 振动特性求解
假设横向振动的位移w0(x,y,t)为
w0(x,y,t)=ejωtW(ξ,η)
(16)
式中:ω为振动频率;W(ξ,η)为振型函数。
基于Rayleigh-Ritz法,可将结构系统的中面位移X0表示为
(17)
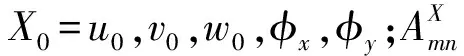
P1(ξ)=χ(ξ),P1(η)=κ(η),
P2(φ)=(φ-H2)P1(φ)
Pi(φ)=(φ-Hi)Pi-1(φ)-ViPi-2(φ),
φ=ξ,η,i>2
(18)
其中,Hi和Vi为系数函数,其表达式分别为
(19)
式中,W(φ)为权函数,通常取W(φ)=1。而χ(ξ)和κ(η)是满足边界条件的多项式函数,具有如下的形式
χ(ξ)=ξp(1-ξ)q,κ(η)=ηr(1-η)s,
ξ=x/a,η=y/b
(20)
对于本文所研究的悬臂条件,可取p=2,q=0,r=0,s=0。
将式(17)代入式(16),并分别令cos(ωt)=1与sin(ωt)=1,可得出结构系统的最大动能Tmax与最大应变能Umax。如此,可定义能量函数E为
E=Tmax-Umax
(21)
求解Ritz参数的极小值,即令能量函数对待定Ritz参数的偏导数为零
m=1,2,…,Mn=1,2,…,N
(22)
结构系统的特征方程可表示为
(K-ω2M)q=0
(23)
式中:K为刚度矩阵;M为质量矩阵;q=(q11,q12,…qij)T为特征向量。
为保证式(23)有非零解,系数矩阵的行列式应等于零,即
det(K-ω2M)=0
(24)
求解式(24),即可得出MVL-FMLP结构的各阶固有频率。将各阶固有频率对应的特征向量q代入式(17),就可获得各阶模态振型。
接着,将刚度矩阵表述成复刚度矩阵的形式,则式(7)~(9)中的刚度矩阵系数可表示为
(25)
式中:i=1, 2, 6;j=1, 2, 6。

ΔU=ΔUm+ΔUf+ΔUv
(26)
式中:ΔUm、ΔUf、ΔUv分别为金属层、纤维层与黏弹性层的耗散能。
根据应变能法,可将结构系统的第r阶模态阻尼比ξr表示为
(27)
接下来,为了求解对MVL-FMLP结构的弯曲振动响应,假设其在图1所示的单点脉冲激励下,可将此脉冲激励看作一个周期极短的正弦半波,其表达式为
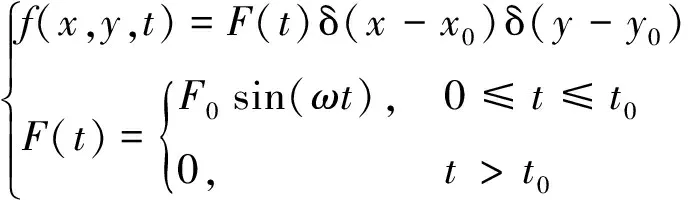
(28)
式中:F0为激励幅值;ω为激励频率;t0为作用时间。
根据振型叠加法,设脉冲激励的时域响应X(t)为
(29)
式中:Wmn(x,y)为模态振型;Tmn(t)为各阶振型分量。
在考虑阻尼的情况下,广义振动微分方程可表示为
(30)
式中,Pmn(t)与Mmn分别为第(m,n)阶广义力与广义质量,其表达式为
在初始条件为零的情况下,对式(30)应用杜哈梅积分可得
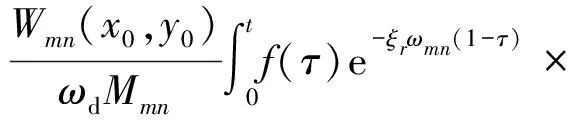
sinωd(t-τ)dτ
(31)
将式(32)代入式(30)即可求解出MVL-FMLP结构的时域振动响应,对其进行快速傅里叶变换(fast Fourier transform,FFT)操作,亦可获得频域振动响应。
2 试验验证与讨论
2.1 试验对象和测试系统
通过真空导流法制备碳纤维板,并切割出两块形状相同的TC300碳纤维/E21环氧树脂板(由3层单向纤维布铺设而成,铺设方式为[0°/90°/0°]),其材料参数为:ρf=1 780 kg/m3,Ef1=136 GPa,Ef2=7.9 GPa,Gf12=Gf16=Gf26=3.39 GPa,υ12=0.3,υ21=0.017,ηf=0.04;进一步,结合购买的两层金属外层和黏弹性层芯层材料,采用树脂作为黏结剂,并在模具的螺栓装配压力下自然固化,最终制备获得5层层合板试件。图2给出了MVL-FMLP结构的振动测试系统,通过模态力锤对板试件进行脉冲激励,并通过激光测振仪获取振动响应信号。当其一端被约束后,在悬臂边界下,该试件的有效测试尺寸为170.00 mm×145.00 mm×4.82 mm,其中,各层厚度为:hm=0.3 mm,hf=1.11 mm,hv=2 mm;金属层材料为铝合金,其材料参数为:ρm=2 700 kg/m3,Em=70 GPa,Gm=26.5 GPa,υm=0.35,ηm=0.008;黏弹性层材料为购买的软性光敏树脂(soft photosensitive resin,SPR),其密度ρv=1 300 kg/m3,微孔结构通过3D打印方式获得,尺寸参数d=0.5 mm,孔间距p=q=2 mm(此时只有一层微孔,可忽略其沿z方向的孔间距m)。另外,利用自行研发的复合材料参数测试仪[24]和迭代辨识方法来测试黏弹性层对应的梁试件的弹性模量和损耗因子等参数,可得:Ev=15.1 MPa,Gv=5.2 MPa,υv=0.47,ηv=0.3。
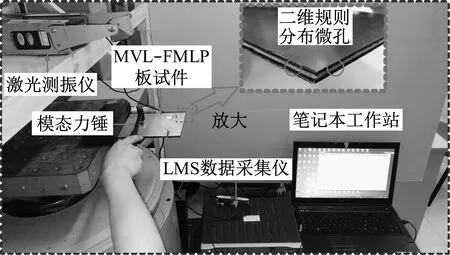
图2 MVL-FMLP结构振动测试现场图
开展振动测试时,首先利用LMS Test.Lab软件中的Impact模块,通过模态力锤对试件进行3次敲击测试,对获得数据进行平均处理后,根据半功率带宽法辨识获得固有频率和模态阻尼比。然后,再利用LMS Test.Lab软件中的Signature模块,进行脉冲激励下振动响应时域信号的采集,并通过FFT获得其频谱数据。
2.2 理论与测试结果对比
试验测试与理论计算获得的板试件的前3阶固有频率和模态阻尼比,如表1所示。对其进行分析可知,固有频率与阻尼比的计算误差分别不超过4.5%和9.7%,初步验证了理论模型在预测频率和阻尼性能方面的正确性和有效性。
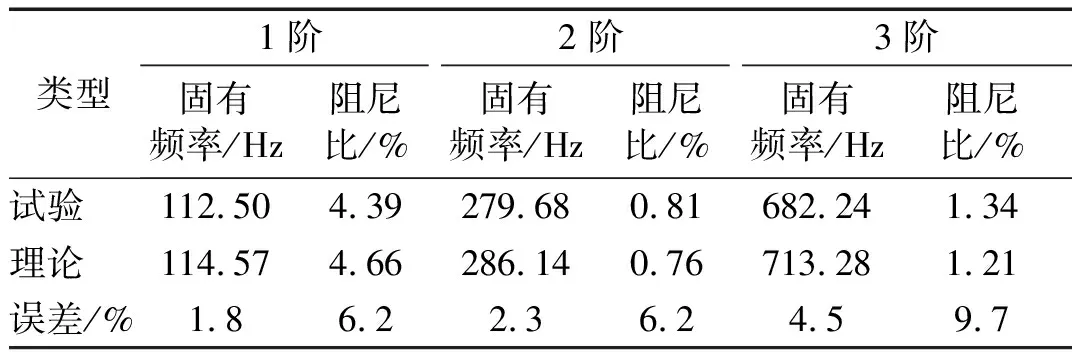
表1 板试件的前3阶固有频率和阻尼比的试验和理论结果
另外,试验测试与理论计算获得的脉冲激励下的激励信号的时域波形,如图3所示。两种方式获得的MVL-FMLP板振动响应信号的时域波形和频谱图,如图4所示。对其进行比较可知,理论与测试获得的结构系统的时域振动响应吻合较好,且频谱图中最大响应峰值误差最大不超过7.5%,进一步验证了该理论模型在预测结构振动响应方面的正确性,可以利用该模型对MVL-FMLP结构的振动特性进行有效预测。
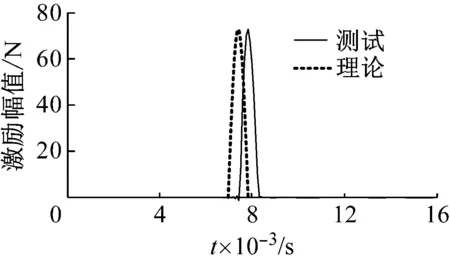
图3 测试与理论计算获得的脉冲激励下激励信号的时域波形
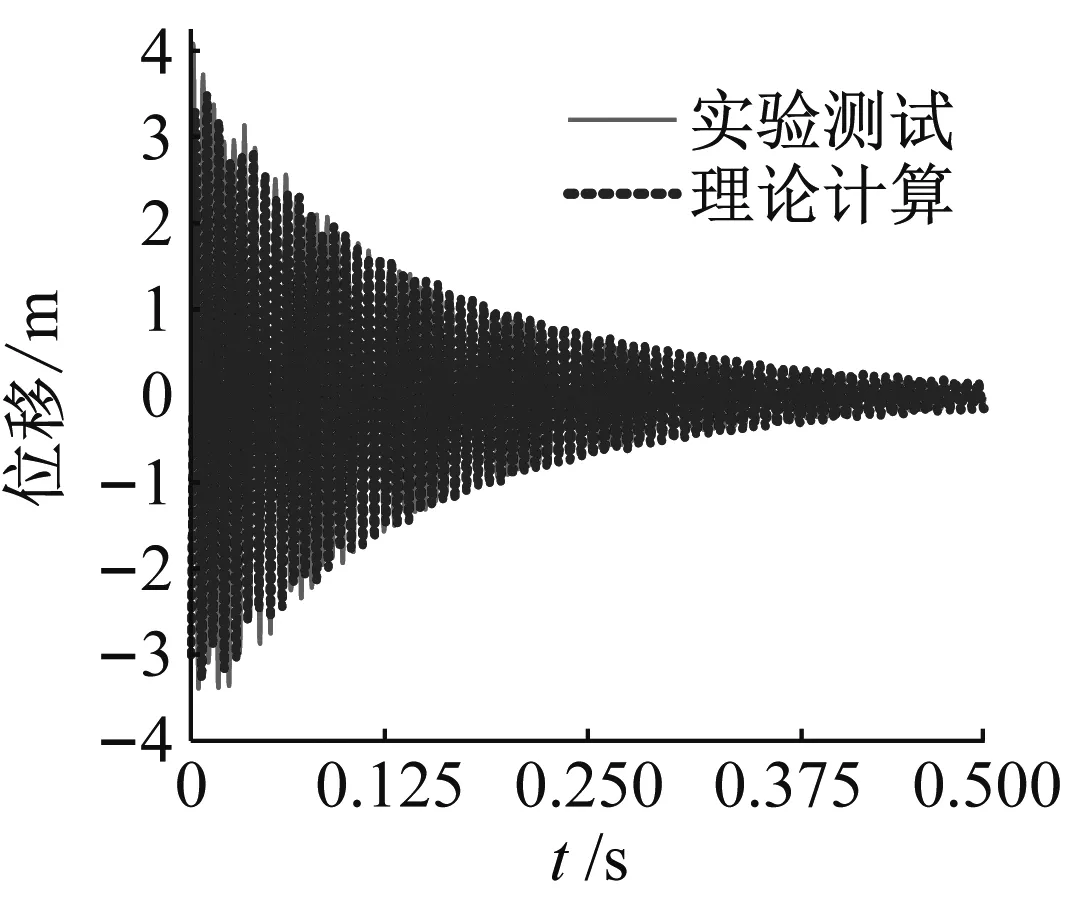
(a)时域信号
2.3 微孔几何参数对结构振动特性的影响
在验证后的理论模型的基础上,改变黏弹性层中二维规则微孔几何参数,研究MVL-FMLP板振动特性的变化规律。此时,计算模型采用的板长、宽、厚为170.00 mm×145.00 mm×4.82 mm,d=0.5 mm,p=q=2 mm,F0=73 N,响应点R1(x1,y1)=(65,120)。脉冲激励下微孔直径与黏弹性层厚度之比d/hv以及孔间距与直径之比m/d的改变,对MVL-FMLP结构前3阶振动响应和阻尼特性的影响规律(由于固有频率受到的影响很小,在此未讨论),如图5所示。由图5(a)可知,随着d/hv的增大,会导致结构系统各阶响应的峰值下降,并提升阻尼性能。将d/hv=0对应的结果作为基准,可知在d/hv=0%~100%内,且前3阶响应峰值最大的下降程度ΔXmax为22.3%,而阻尼性能的最大上升程度Δξmax为17.9%。另外,对图5(b)分析可知,随着m/d增大,结构系统各阶响应的峰值上升,而各阶阻尼性能出下降的趋势。此时,前3阶响应峰值最大的增大程度ΔXmax为28.2%,而阻尼性能的最大下降程度Δξmax为17.1%。产生上述现象的原因是由于d/hv的增大或m/d的减小,会导致式(6)中黏弹性层中Ev与Gv的减小,进一步会导致结构阻尼比的增加和振动响应的下降。
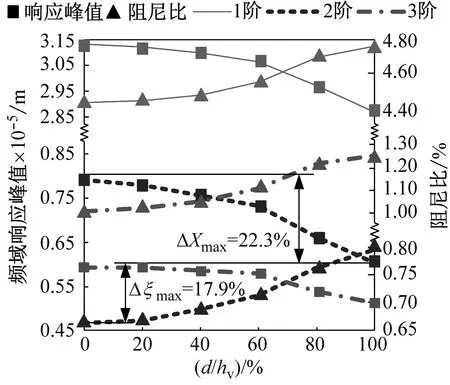
(a)d/hv
3 结 论
本文提出了MVL-FMLP结构的振动分析模型,并通过试验验证方式证明了该模型在预报固有频率、振动响应和阻尼特性方面的正确性和有效性。同时。讨论了该结构包含的黏弹性层中微孔几何参数的改变对其振动特性的影响规律。研究发现随着微孔直径与黏弹性层厚度比的增大,结构前3阶振动响应峰值减小且相应的阻尼比上升;而随着微孔间距与直径比的上升,结构的响应和阻尼性能呈现相反的变化趋势。本文所建立的数学模型及其相关分析结论,可为带有规则微孔构型的含黏弹性芯层的纤维金属混杂层合结构的减振设计与性能优化,提供理论与实践的参考。

