支管流致噪声干扰下的复值域EFastICA管道泄漏声定位技术研究

刘名杨，杨 进，郑 伟，樊恩东

(重庆大学 光电工程学院 光电技术及系统教育部重点实验室，重庆 400044)

供水管道泄漏不仅带来经济损失、环境污染的问题，甚至对城市居民的健康安全构成威胁，更重要的是造成了水资源浪费问题。造成管道泄漏的原因主要包括管道老化、化学腐蚀、外力损伤以及疏于管理维护。据2020年《2020—2026年中国城市供水行业深度调研及投资前景分析报告》指出[1]，中国大陆地区平均每年城市管网泄漏率达15.3%，部分城市甚至超过25%，这高于其他许多发达国家标准。

在管道泄漏检测领域中，声发射检测技术以其成本低、非开挖、高效率的特点被得到广泛应用。经典的管道声发射检测如图1所示，声学或振动传感器紧贴于泄漏管道两端获取泄漏信号[2]。但在实际的泄漏检测中，泄漏声发射信号可能会受到各种各样的管道外部和管道内部噪声干扰，外部噪声有汽车噪声、机器噪声、人为噪声等等，内部噪声以管道自身噪声为主，如支管流致噪声等其他非直管道接头引起的噪声。

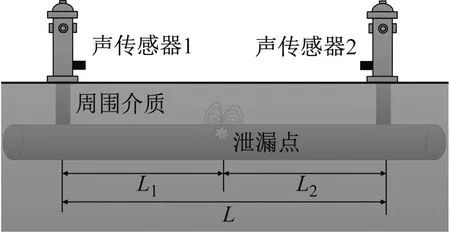
图1 经典管道声发射检测示意图

为了有效去除噪声、提取源泄漏信号，目前的研究大多采用小波分析[3-4]、EMD(empirical mode decomposition)类[5-6]、VMD(variational mode decomposition)类[7-8]等算法来去除或抑制噪声。Ting等[9]提出一种改进的双树复小波变换技术(dual-tree complex wavelet transform, DTCWT)将含噪泄漏信号分解成若干个子信号，利用软阈值去除子信号中的噪声，再重建泄漏信号；郭晨城等[10]提出改进的 EMD 信号增强方法对含噪泄漏信号进行信号增强处理，该方法虽然不需要掌握泄漏信号和噪声信号的先验信息，但要对其特征进行数学假设解析；Diao等[11]将粒子群算法和最大熵法结合起来，优化了VMD的惩罚因子和模态数选择，随后对含噪泄漏信号进行分解重构，去除背景噪声以提取源泄漏信号。

这些方法一般都是从直的泄漏管采集泄漏信号，且认为混合泄漏信号是等效于噪声同源泄漏信号的叠加，它们对噪声的处理过程是一个去除或抑制加性噪声的过程。但是，管内噪声和泄漏声信号耦合叠加以后，以管道作为传播信道进行传播，其传播过程是一个卷积过程，因此，对含管内噪声的泄漏信号进行分解处理是一个解卷积的过程。此外，包含支管流致噪声在内，所有的管道内部噪声都属于一种后验噪声，其时域、频域和概率密度特征都是未知的。但前述几种方法都是基于外部噪声的功率谱特征、时频特征等先验信息可知或假设可知，以实现对声发射信号进行处理。因此，上述方法技术不能直接被运用于对管内噪声的抑制或去除。在支管泄漏检测中，泄漏信号和支管流致噪声具有少量的先验知识，且支管流致噪声和泄漏信号耦合以后与传播信道(管道)之间是卷积关系，因此，从含支管流致噪声的泄漏信号中分离出源泄漏信号来定位管道泄漏是一个典型的盲解卷积分离(blind deconvolution separation, BDS)问题[12]。

在盲分离中，快速独立主成分分析(fast independent component analysis，FastICA)因收敛速度快，且分离性能好，被得到广泛应用。与此同时，一些改进的FastICA也被得到广泛应用。Jiménez-González等[13]将时空ICA(space and time independent component analysis, ST-ICA)与FastICA相结合提出ST-FastICA，实现对胎儿心电图信号的高质量分离；Dong等[14]将四阶矩累积量的联合对角化运用于FastICA算法中，大大降低FastICA的运算量；Xie等[15]提出一种改进的复数域FastICA算法，该方法在分离矩阵的更新迭代过程中引入噪声因子，实现对低信噪比混合信号的分离。

但上述主成分分析(independent component analysis，ICA)类盲分离算法大多未考虑待分解信号的概率分布特征，固定的选择非线性函数g来构建算法的代价函数和迭代学习规则，这样做有两大缺点：其一是算法根据观测样本的概率密度特征去估计得分函数(同样由g构建)有一定的难度；其二是固定选择的非线性函数g在观测样本空间内不一定是连续可导的。这使得算法对混合信号的分离效率和质量受到一定影响，进一步使得管道泄漏定位精确度受限。

为了从含有支管流致噪声的泄漏信号中高效地分离提取源泄漏信号，文中提出一种新颖的复数域盲分离处理方法，即复值域高效快速独立主成分分析(complex efficient fast independent component analysis，C-EFastICA)方法。该方法基于现有的高效快速独立主成分分析(efficient fast independent component analysis，EFastICA)算法[16-17]，EFastICA作为FastICA的一种改进算法，它与FastICA相比：① 其计算复杂度与FastICA保持相当，但收敛速度略快于FastICA；② EFastICA分解精度更高，EFastICA根据信号的广义高斯特征自适应地选择非线性函数g来建立代价函数和迭代学习规则，对信号的分解程度能到达克拉美罗下界。EFastICA经复值化扩展后得到C-FastICA(complex FastICA)，C-FastICA同样具有分解程度高、分解速度快的优点。文中通过对泄漏信号和噪声信号进行广义高斯特征计算，发现泄漏信号和噪声信号均是超高斯信号，C-EFastICA根据其超高斯特性选择非线性函数构建代价函数和迭代学习规则。混合泄漏声信号经C-EFastICA分解处理以后，再使用互相关技术得到时延估计值，结合已知的泄漏声传播速度完成泄漏定位工作。

1 支管流致噪声与含噪泄漏信号频谱特征研究

本章采用管径100 mm的供水管道采集支管流致噪声和含支管流致噪声的泄漏声信号。100 mm管径的管道系统实物图如图2所示，包含支管接头和模拟泄漏点，其中模拟泄漏点为DN15泄漏阀(泄漏孔直径为15 mm)。由图2可知，100 mm管径管道的模拟泄漏点距离支管接头为60 m。我们将管内压强控制在0.6 MPa左右，利用集成有加速度计的数据采样设备以采样率10 kHz对信号进行采样。

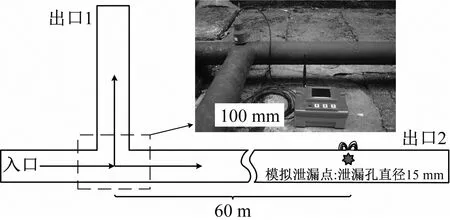
图2 测试管道系统示意图

本试验的主要过程如下：

步骤1打开模拟泄漏点，放置传感器在泄漏点附近，获取含有支管流致噪声的泄漏信号；

步骤2关闭模拟泄漏点，放置传感器在支管接头上，仅获取支管流致噪声；

步骤3分别计算含支管流致噪声的泄漏信号和支管流致噪声的频谱。

100 mm管径的含噪泄漏信号和支管流致噪声频谱，如图3所示。从图3中可知，支管流致噪声的主谱峰位于100～2 000 Hz频带内；而含噪泄漏信号的主频带位于120～3 300 Hz，其中500～1 500 Hz频带内(小矩形框内)具有一个显著的谱峰，这个显著的谱峰则是由支管流致噪声引起的。上述结果表明：① 泄漏信号的主频带要比支管流致噪声的主频带更宽，进一步说明泄漏信号的随机性要比支管流致噪声的随机性更强；② 当管道存在支管接头时，支管流致噪声对于泄漏检测而言是一种不可忽略的噪声干扰。支管流致噪声和泄漏信号的概率密度分布图，如图4所示。图4中支管流致噪声和泄漏信号的概率密度均呈现中心部分又窄又高，而尾部拖得很长的特征，这是典型的超高斯信号概率密度特征。为此我们引入一个四阶矩来度量信号的高斯性

(a)支管流致噪声频谱

图4 支管流致噪声信号、含噪泄漏声信号概率分布

(1)

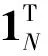
(2)

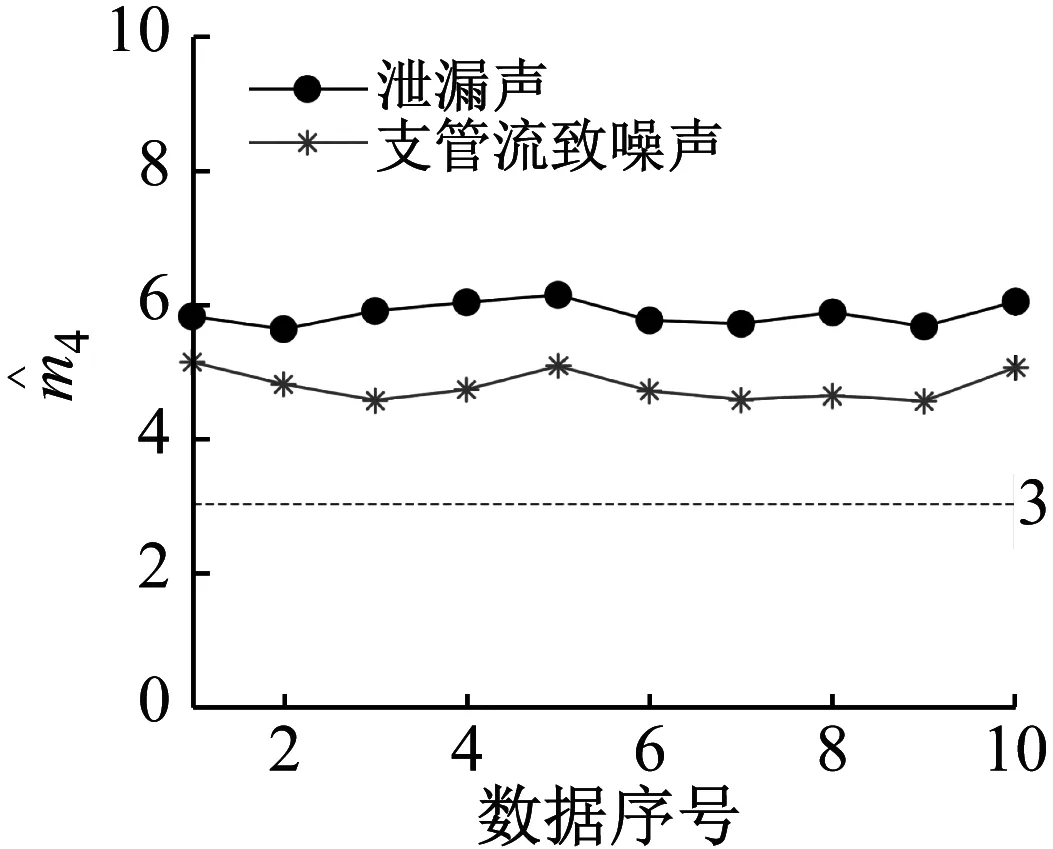
图5 泄漏声信号和支管流致噪声的值计算结果

2 算法理论背景

根据泄漏特征，我们建立泄漏时域卷积模型如下

(3)

式中：s(n)=sleak(n)+sbranch(n)，n1(n)和n2(n)为背景噪声；a(n)和b(n)为系统混合矩阵，为了使计算更方便快捷，我们将时域卷积的混合模型变换到频域中的乘积模型，再进行频域内的盲分离。频域混合模型如下

(4)

通常将z省略，则有

(5)

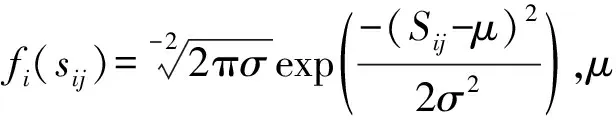
2.1 C-EFastICA算法

根据式(5)，暂不考虑背景噪声N1和N2，即认为背景噪声在进行盲分离以前已经通过其他方法技术降低到可以忽略的程度[18-19]，此时式(5)简化为

(6)

略去下标，将混合矩阵A与B用混合矩阵C替换整理得到

x=CS

(7)

信号源盲分离估计就是指在混合矩阵C和源信号S未知的条件下，求一个分离矩阵W，使得W对观测信号x有如下线性变换

u=Wx

(8)

设观测信号和分离矩阵、输出信号均为复数形式

x=xr+jxi

(9)

W=Wr+jWi

(10)

u=ur+jui

(11)

令xH为x的复共轭转置，wH为w的复共轭转置，且它们的实部和虚部不相关，则有E(wwH)=I, 设此时的输出信号模型为u=wHx，N个向量wi按列组成了W。

本算法第一步是对信号去均值处理和预白化处理

(12)

第二步，根据信号的广义高斯特征选择非线性g函数。非线性函数有以下3种可供选择

(13)

由于泄漏信号和支管流致噪声均是超高斯信号，则此处选择非线性g函数为g(x)=xexp(-η3|x|)，此函数在超高斯样本空间内连续可导，令参数η3为3.348。

(14)

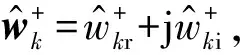
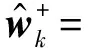
(15)

最终整理得到

(16)

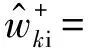
(17)

下一步是计算

(18)

(19)

(20)

(21)

(22)

式中，k=1,…,d。计算

(23)

式中，k，l=1,…,d。接下来计算

(24)

(25)

(26)

(27)

算法1Complex-Efficient FastICA(C-EFastICA)

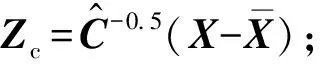
初始化w=randn+j·randn;

根据g(x)=x/(1+x2);

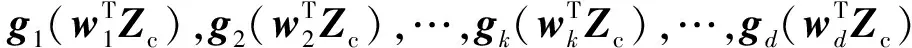
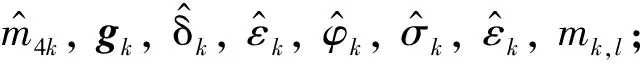
Foriter≥0

计算

收敛、停机！

3 泄漏定位检测试验

3.1 C-EFastICA算法运用于管道泄漏定位

本节将利用加速度传感器采集两路含支管流致噪声的泄漏信号，再利用C-EFastICA算法对含支管流致噪声的泄漏信号进行分离，主要的泄漏检测步骤如图6所示。将根据该流程图的流程，利用实际的100 mm管径供水管道进行试验研究。

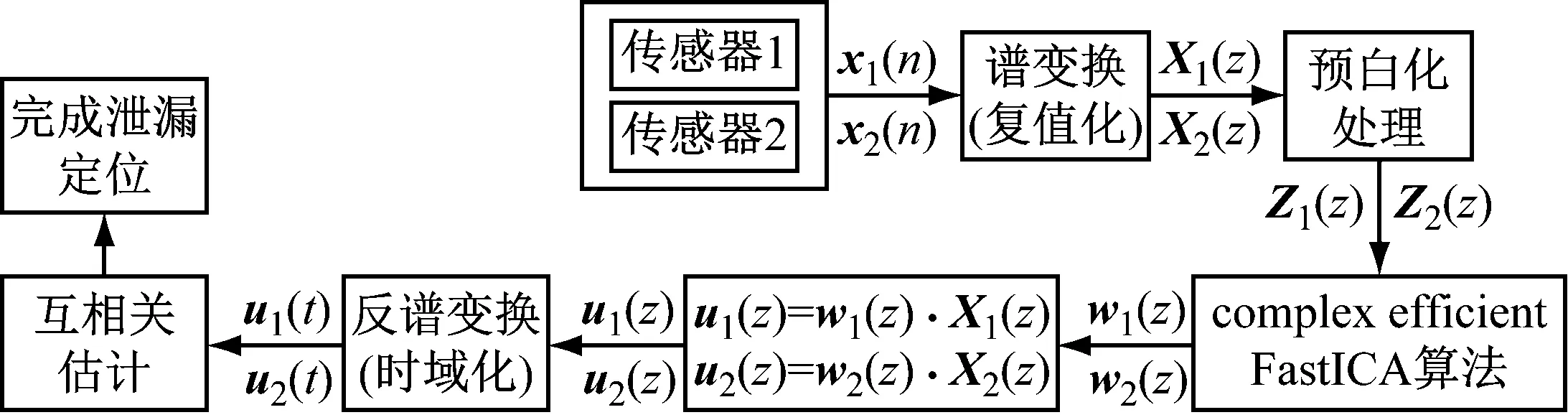
图6 泄漏定位检测流程图

3.2 试验条件

试验选择直径为100 mm、长度70 m的铸铁供水管道采集泄漏信号，管道内部压力范围为0.55～0.60 MPa，入口流速约为2 m/s，模拟泄漏点以DN15小口阀门(泄漏孔径15 mm)代替，且模拟泄漏点距离传感器1有42 m，信号采集设备采用自主研制的泄漏信号数据采集设备，数据采样率设置为10 kHz，详细参数设置如表1所示。泄漏检测系统示意图，如图7所示。两路传感器被放置在管道两端尽头，采集到的泄漏信号经无线传输到主机。两路传感器和支管接头实物图，如图8所示。

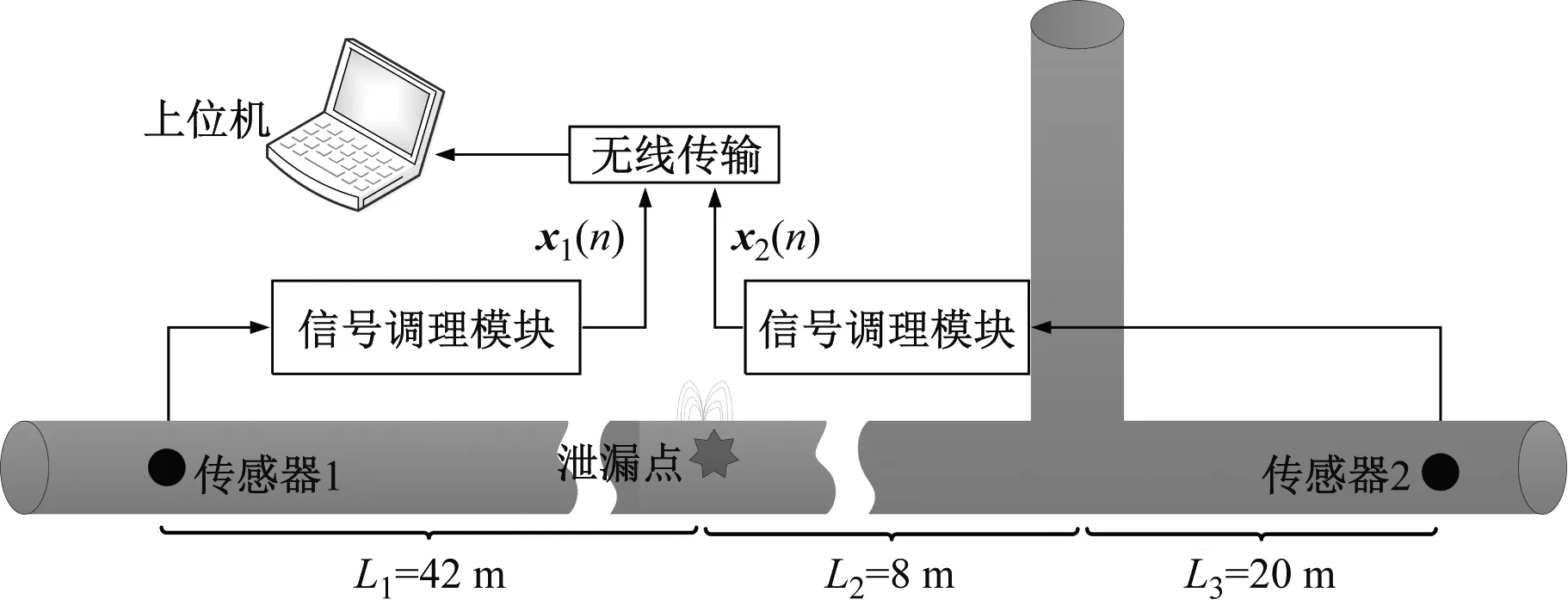
图7 泄漏检测系统示意图(m)

(a)

表1 试验中的详细参数条件

3.3 泄漏定位过程

两路传感器1、传感器2采集得到的含支管流致噪声的泄漏信号频域形式如图9所示。

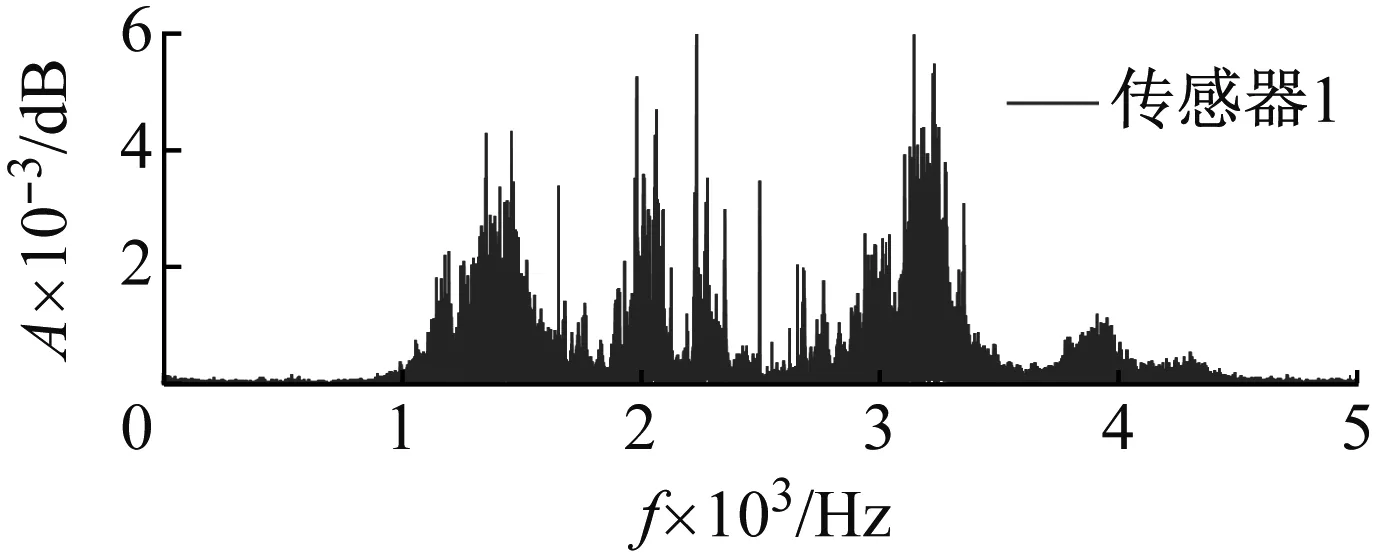
(a)

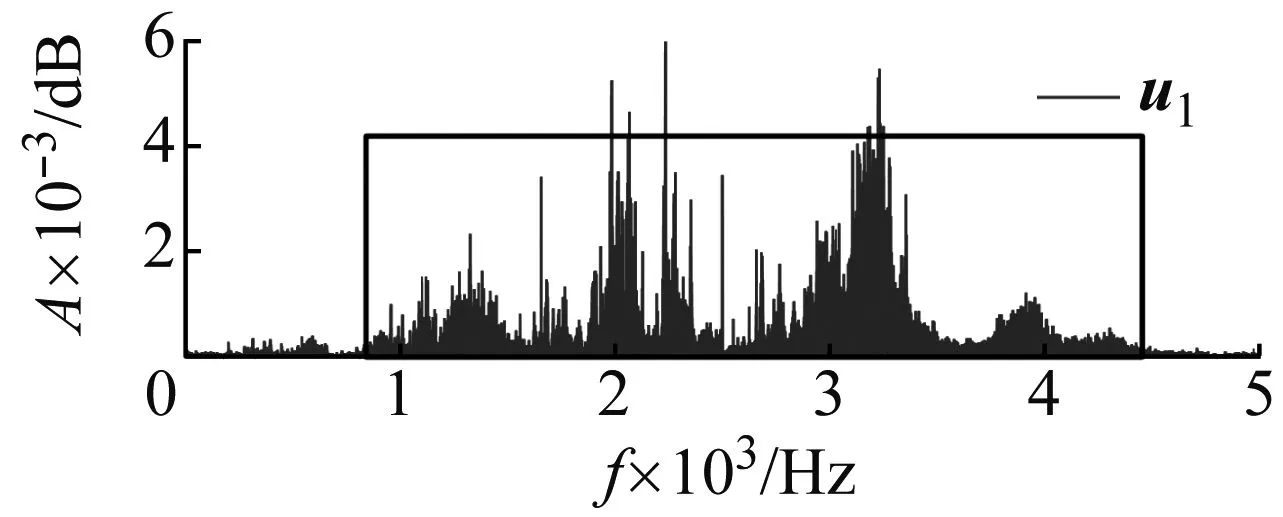
为了证明C-EFastICA算法的分离性能，我们利用已知的C-FastICA算法[20]对含噪泄漏信号进行分解处理。在对含噪泄漏信号进行分解前，必须对含噪泄漏信号进行预处理，抑制加性噪声n1和n2对信号分解的影响，更多关于抑制加性噪声的细节详见朱建斌等和张艳艳等的研究。C-EFastICA算法、C-FastICA算法对含噪泄漏信号(以传感器1采集的源数据为例进行分解处理)的分解结果分别如图10和图11所示。

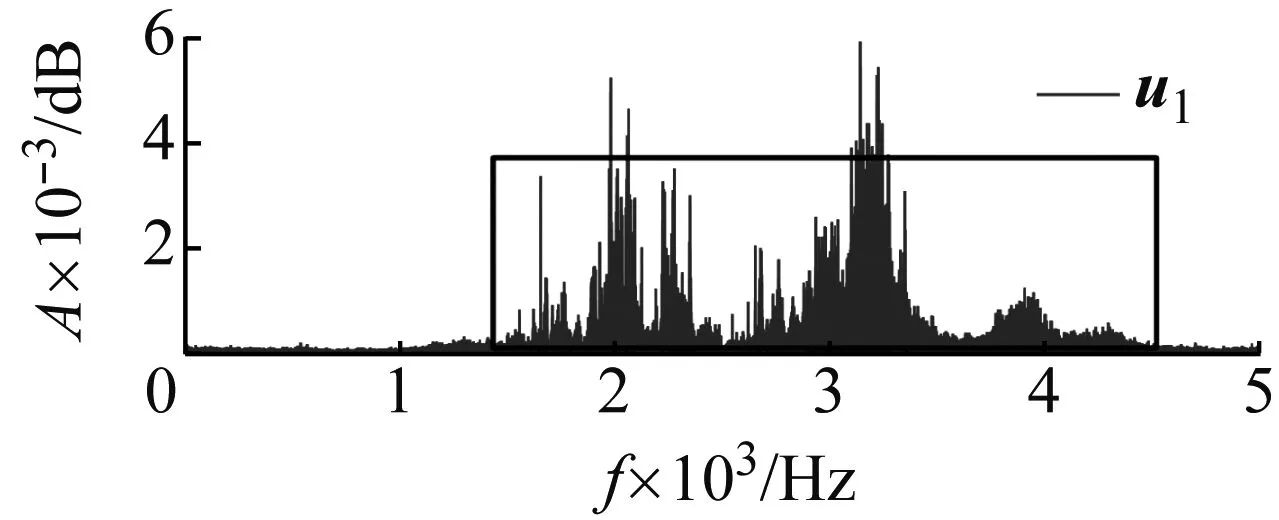
(a)

(a)

为了评估算法的收敛速度，码间串扰(inter-symbol interference, ISI)的概念被引入，其定义如下

(28)

式中：cij为全局系统矩阵C中的第(i,j)个元素，当每个通道的ISI输出曲线越接近0的时候，算法越收敛。C-EFastICA和C-FastICA的两路通道的ISI输出曲线，如图12所示。从图12可知，C-EFastICA在300步左右就收敛了，而C-FastICA则要在400步左右时才收敛，由此可见，C-EFastICA的收敛速度要快于C-FastICA。

(a)

此处引入串音误差PI来比较C-EFastICA算法和C-FastICA算法的分离性能，PI值越接近0说明算法对混合信号的分离程度越高，PI定义如下

(29)

式中：M为源信号的数量；cik为C=W·A的元素，A为混合矩阵，W为算法分离得到的分离矩阵。将C-EFastICA算法和C-FastICA算法分别对含支管流致噪声的泄漏信号再进行50次分离试验，得到试验结果如图13所示。

图13 C-EFastICA与C-FastICA分别进行50次盲分离试验的PI值

从图13可知，C-EFastICA的PI系数均小于C-FastICA的PI系数，C-EFastICA的PI系数中位数在0.125左右，而C-FastICA的PI系数中位数在0.225左右，即可表明C-EFastICA对含噪信号的分离程度越彻底，分离出的源泄漏信号所含泄漏特征更多。

u1的谱成分主要分布于1 600～4 500 Hz的有效频带内，而u2的谱成分主要位于1 000～2 300 Hz区间，见图10。图11中，分离信号u1和u2相比，u1的频谱特征位于1 000～4 500 Hz，u2的谱特征位于1 000～2 200 Hz。为了从分离结果中区分泄漏源信号和噪声源信号，我们对分离结果计算了样本熵[21]，以熵值的大小差别区分泄漏源信号和噪声源信号。这是由于源泄漏声信号较支管流致噪声往往具有更大的随机性，即源泄漏信号的有效主频带比支管流致噪声的主频带更宽。从图3也可看出泄漏声信号的频率成分比支管流致噪声也更丰富，所以泄漏信号的熵值应大于支管流致噪声。计算C-EFastICA算法、C-FastICA算法对含噪泄漏信号分解得到的u1和u2的样本熵(SampEn)值如表2所示。在表2中，u1的样本熵均大于1.2，而u2均不超过0.9，因此我们认为u1是泄漏源信号，u2是支管流致噪声。

表2 不同算法分离结果的样本熵值

以同样方式对传感器2采集得到的含噪泄漏信号进行处理，得到另一路源泄漏信号，对于得到的两路源泄漏信号，利用互相关技术对它们进行处理。如图7所示，传感器1距离泄漏点的距离L1=42 m，已知泄漏声速在铸铁管道中的传播速度为c=1 495 m/s，时延估计τ由互相关估计得到，因此泄漏点距离传感器1的距离由下式计算得到

L1=(L-cτ)/2

(30)

式中，L=L1+L2+L3=70 m。C-EFastICA、C-FastICA算法分解得到的泄漏源信号的互相关估计定位结果图，如图14(a)、图14(b)所示。两路混合信号经传统的直接互相关算法(direct cross-correlation, DCC)的定位结果图，如图14(c)所示。

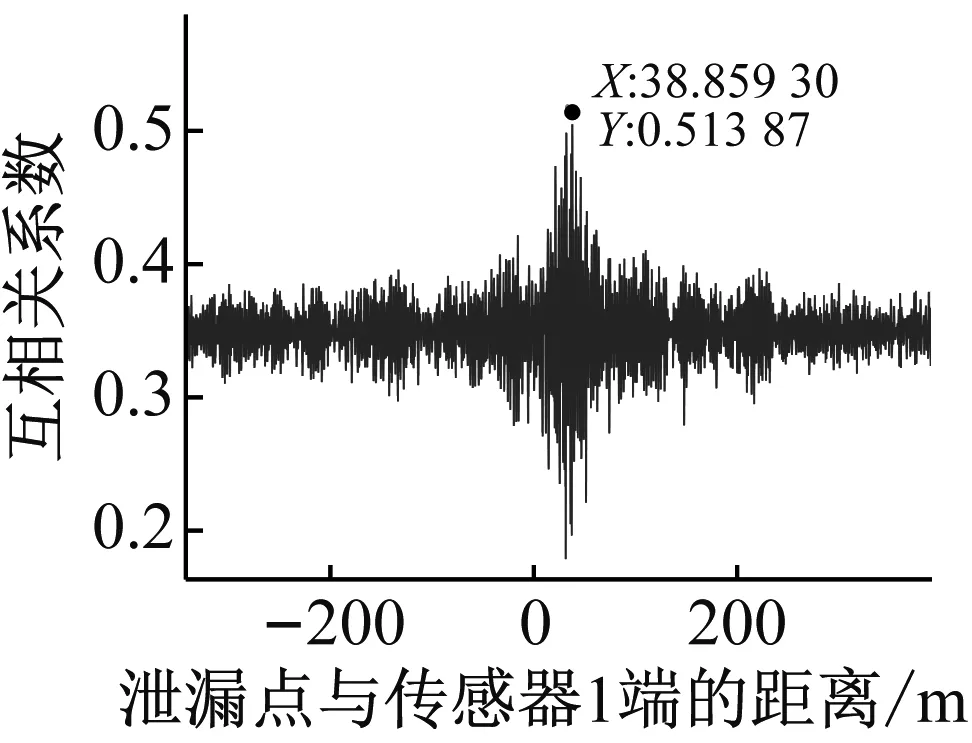
(a)C-EFastICA算法的互相关估计定位结果

由图14(a)、图14(b)可知，只有在图14(a)中的峰值最接近于真实泄漏点距离。对比图14(a)和图14(b)，在图14(c)中的定位结果误差最大，这是由于未对泄漏信号中的支管流致噪声进行处理，支管流致噪声对互相关估计产生了较大的影响。为了进一步验证C-EFastICA对混合泄漏信号的分离性能优于C-FastICA，本试验被重复数次，定位结果如表3所示。

表3中，δ为相对误差，C-EFastICA的定位相对误差均不超过12%，而C-FastICA算法的定位误差达到15%，所以C-EFastICA算法的定位精度高于C-FastICA算法。而直接互相关定位法由于受噪声影响严重，定位相对误差达到60%以上，甚至无法完成定位。

表3 不同算法对分支管道泄漏点的定位相对误差

4 结 论

针对分支泄漏管道中存在支管流致噪声对漏点定位干扰的问题，文中提出使用基于EFastICA算法的C-EFastICA对含支管流致噪声的泄漏信号进行分离计算，得到源泄漏信号，结合先验声速和管道长度完成漏点定位，通过试验证明该方法的可行性，得到以下结论：

(1)当管道中存在分支接头时，即泄漏信号中混有支管流致噪声时，采用传统的直接互相关方法对管道进行漏点定位误差较大，甚至无法完成定位。说明了分支管道泄漏定位中，支管流致噪声对定位的影响不可忽视。

(2)试验证明，泄漏信号和支管流致噪声均是超高斯信号。与其他ICA类算法固定选择非线性函数不同，C-EFastICA能根据信号的广义高斯特性自适应地选择非线性函数构建迭代学习规则，即C-EFastICA算法是基于混合泄漏信号的物理特征进行分解运算的。

(3)所提出的C-EFastICA算法相较于同类型的C-FastICA具有更快的收敛速度，在对混合信号的分解程度上也具有更高的水平。