水力发电机组轴系不确定性量化及参数敏感性分析
闫懂林,郑 阳,刘宛莹,陈启卷
(武汉大学 动力与机械学院,武汉 430072)
水力发电机组作为水电站中能量转换的枢纽,其故障或事故,会直接影响水电站乃至电网的安全稳定[1]。因此,为了避免一些重大安全事故地发生,对水力发电机组结构特性和动力学响应进行研究十分必要。
到目前为止,已经有大量学者致力于水力发电机组结构建模及动力学特性的分析研究。Xu等[2]综合考虑了阻尼、油膜和磁拉力对水力发电机组的影响,以拉格朗日方程为基础建立了一个机组轴系的分数阶非线性动力学模型,并讨论了参数变化对机组非线性特性的影响效应;Huang等[3]提出了包含不对中和质量偏心故障的水力发电机组转子系统数学模型,并分析了故障耦合作用下的系统动力学特性;Zhang等[4]推导了不同荷载条件下的水电机组水力激励的数学表达式,研究了机组突增负荷过程中轴系的振动响应特性;Yan等[5]建立了包含叶片的贯流式水力发电机组轴系统模型,讨论了叶片对机组轴系振动特性的影响机理。总的来说,这些研究可以为水力发电机组的设计、优化、运行和维护提供一定的参考。但值得注意的是,当前的研究主要都是基于确定性模型和方法展开,很少提及参数不确定性的影响。实际上,对于水力发电机组来说,存在许多不确定性因素,如制造公差、材料特性的固有随机性、磨损、应力变化、随机载荷等,这些不确定性对机组的安全和可靠性会造成潜在的威胁[6]。而现有的确定性分析方法对水力发电机组的不确定性问题可能是局限的或无效的,因此,为了探究不确定参数对机组结构性能和动力学响应的影响,需要引入不确定性分析的方法和理论来展开研究。同时,考虑到结构的不确定性较难发现,其破坏性在实际工程中也最为显著,对其研究也相对较少,故本研究将重点研究机组结构参数的不确定性。
大量研究表明,不确定性量化和参数敏感性分析是探索物理系统不确定问题的两种有效方法[7]。一方面,不确定性量化是用来评估系统输入到输出过程中不确定性的传播,通常采用输出响应的均值、方差和置信区间作为量化指标[8];另一方面,参数敏感性分析是为了量化不确定参数对系统输出不确定性的贡献,可以分为局部敏感性分析和全局敏感性分析。当模型的输出不确定性比较突出,或者模型具有较强的非线性时,全局敏感性分析比局部敏感性分析更具优势[9],主流的全局敏感性分析方法有回归分析法、Morris筛选法、Sobol法、傅里叶幅度检验法和扩展傅里叶幅度检验法等。考虑到水力发电机组轴系统是一个复杂的非线性系统,这里将利用全局敏感性分析来讨论机组结构参数不确定对系统输出的影响效应。
对于高自由度的水力发电机组转子结构系统,在计算不确定性参数的各阶敏感性指标时,传统的暴力Monte-Carlo模拟法需要大量的样本,计算成本很高甚至难以接受。为了解决这一问题,本文将引入基于多项式混沌展开的代理模型技术[10],建立描述机组不确定结构参数与输出变量之间关系的代理模型用于不确定性量化研究。同时,由于多项式混沌展开的形式可以很容易地转化为方差分解的形式,只需对展开系数进行简单的后处理便可以得到参数的敏感性指标,避免了大量的样本计算,故本文将采用这种方法来对机组结构参数不确定性的影响展开研究。
综上所述,本文提出了一套以广义多项式混沌展开为基础的水力发电机组轴系建模、不确定性量化和参数敏感性分析的统一框架。主要贡献如下:① 将水力发电机组轴系结构特性和动力响应的研究扩展到不确定性范围,并建立了一个包含不确定性信息的机组轴系动力学模型;② 对于不确定参数下的机组结构固有特性和振动响应的不确定性量化,除了广泛使用的均值、方差和各阶统计矩外,还利用最大熵原理得到了随机输出的具体概率密度函数表达式;③ 基于广义多项式混沌方法,快速获得了不确定参数对固有频率(静态响应)和振动响应(动态响应)的全局灵敏性指标,指导水电机组的实际生产实践。
1 水力发电机组轴系建模
水力发电机组的轴系简化结构如图1所示,其动力响应主要由轴系、边界条件和外部激励决定,下面将分别建立各子单元的模型,并将其组成完整的轴系动力学模型。

图1 机组简化结构图
1.1 轴系统
在轴系中,主要包括转轴、发电机转子和水轮机转轮,这里将采用有限元法建立它们的模型。
对于转轴,采用2节点8自由度的Timoshenko梁单元进行建模,其质量矩阵M(e),刚度矩阵K(e),和陀螺矩阵G(e)见文献[11],下标(e)为单元矩阵。梁单元每个节点有两个平移自由度(x,y)和两个旋转自由度(θx,θy),对于第i个单元,其坐标可以写成ue=[x(i),y(i),θx(i),θy(i),x(i+1),y(i+1),θx(i+1),θy(i+1)]。
发电机转子和水轮机转轮的质量矩阵分别为
Mrotor=diag{m1,m1,Jd1,Jd1}
(1)
Mrunner=diag{m2+mwater,m2+mwater,Jd2,Jd2}
(2)
式中:m1和m2分别为发电机转子和水轮机转轮的质量;Jd1和Jd2分别为它们的截面惯性矩;mwater为水体的附加质量。
发电机转子和水轮机转轮的陀螺矩阵可以表示为
(3)
(4)
式中,Jp1和Jp2分别为转子和转轮的极惯性矩。
根据这些子单元的矩阵,可以构造出机组轴系的完整质量、刚度和陀螺矩阵,构造过程如图2所示。图2中从左上角到右下角的6个节点分别为:上导轴承、发电机转子、下导轴承、联轴器、水导轴承及水轮机转轮。M(e)iL和M(e)iR为单元质量矩阵M(e)的左上角和右下角子矩阵,G(e)iL和G(e)iR为单元陀螺矩阵G(e)的左上角和右下角子矩阵,n1~n5为叠加的单元矩阵个数。

图2 轴系整体矩阵的装配
最后,考虑到水力发电机组是一个多自由度系统,其阻尼采用瑞利阻尼理论进行假设,具体的计算方法和公式见文献[12]。
1.2 边界条件
机组轴系的边界条件主要为各个导向轴承提供的维持轴系旋转的支撑力,以油膜力[13]的形式表示
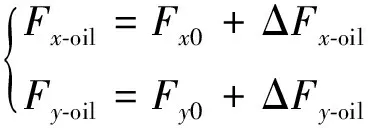
(5)
式中:Fx-oil和Fy-oil分别为x和y方向的油膜力;Fx0和Fy0为静止工作点的油膜力;ΔFx-oil和ΔFy-oil为轴颈偏离静止工作点引起的油膜力增量,其可以用式(6)计算

(6)
式中:kij(i,j=x,y)为刚度系数;dij(i,j=x,y)为阻尼系数;x,y为轴向位移。
1.3 外部激励
外部激励对水力发电机组的动态响应有明显的影响,在本研究中,考虑了质量偏心和不平衡磁拉力两种最典型的激励。具体的模型表达式见Xu等和Zhang等的研究。
1.4 运动方程
基于1.1节~1.3节各个子模型,机组在确定性框架下的轴系动力学模型可以写为
(7)

考虑到机组结构参数的不确定性,在不确定性框架下,水力发电机组的运动方程可表示为
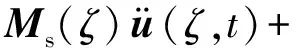
(8)

2 广义多项式混沌展开
2.1 展开式
假设Y=Y(ξ)为一个随机物理模型,ξ为输入随机变量的集合,ξ= {ξ1,ξ2, …,ξd},其中的ξi为第i个输入参数,则该模型的输出响应可以用多项式混沌方法重构[14]为
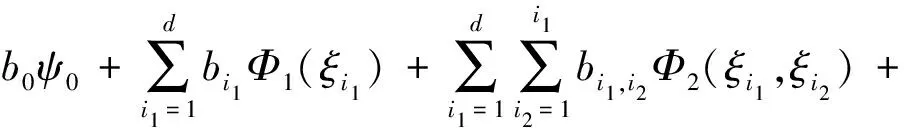
(9)
式中:Y为系统的输出响应;d为随机输入的个数;b0,bi1,i2,…为展开系数;Φn(·)定义了n阶多项式;ψ0为基函数;i1,i2,…为各参数展开项编号。
对式(9)中各项进行重新排序,并进行有限项截断,则原模型可以近似表示为
(10)
式中:r为截断维度;Nd为多维索引的集合;α= {α1, …,αd|αi≥0}为Nd中包含d个元素的多维指标;Ad,r为一个根据r和d定义的区域;βα为重排后的多项式系数;ψα(ξ)为正交基函数,对于有多个随机输入的问题,基函数可通过张量积[15]进行构造。
截断后的多项式混沌展开项数由截断维度和随机变量个数决定,用式(11)计算
(11)
当多项式混沌展开项数确定后,式(10)可以写成一个更紧凑的形式
(12)
式中:β为展开系数的向量,β= {β0, …,βN-1}T;ψ(ξ)为基函数的向量,ψ(ξ)= {ψ0(ξ), …,ψN-1(ξ)};βj为整理后的展开系数;ψj(ξ)为对应的基函数。
2.2 展开系数
假定Yn= {Y1,Y2, …,Yj,…,Yn}T为系统在n个样本ξ= {ξ1,ξ2, …,ξn}下的输出矢量,各实际值与估算值之差ε越小,估计越准确,所以对多项式混沌展开系数的总体估计可以转化为如下的最小化问题
(13)
式中:Yj为第j个样本下的系统输出响应值;ξj为第j个输入样本。
式(13)的最优解即多项式混沌展开系数可以用式(14)计算
β=(HTH)-1HTYn
(14)
式中:Yn为n个样本下的系统输出矢量;H为辅助计算矩阵,其可以表示为
(15)
3 不确定性量化和全局敏感性分析
3.1 不确定性量化
最大熵原理表明:为了获得具有部分已知信息事物的概率分布形式,在约束条件下,选择熵最大的概率分布是最优的。在本研究中,对于原点矩确定的随机输出响应,有多个不同的概率密度函数与之对应,其中最优概率密度函数是熵值最大的一个。换句话说,对不确定系统随机输出的概率密度函数的求解可以转换为如下的优化问题

(16)
式中:H为熵;f(x)为随机变量x的概率密度函数;μs为s阶原点矩;下标s为原点矩的阶次;Ps(x)为已知约束条件下的基函数。
利用拉格朗日乘子法求解式(16),可以得到最优的概率密度函数表达式为
(17)
式中:ηj为待定系数;Pj(x)为第j阶的函数;S为展开的最大阶次。
Abramov的研究表明,幂函数Ps(x)=xs可以作为基函数用于求解概率密度函数,且四阶原点矩已经可以保证足够的精度,故输出响应的概率分布函数可以写成
(18)
3.2 全局敏感性分析
定义一个在Ad,r中的多维指标Li1,…,ie为
Li1,…,ie=

(19)
基于式(19),截断的多项式混沌展开式式(10)可以被重新组织为标准的方差分解形式

(20)
所以,基于方差的各阶敏感性指标可由式(21)直接计算得到
(21)
式中:V(Y)为输出的总方差;Sik为主效应指标;Si1,…,ie为交互效应指标。
而总的敏感性指标为
(22)
4 数值研究
包含不确定参数的水力发电机组轴系固有特性及动力学响应不确定性量化及全局敏感性分析的具体流程,如图3所示。依据文献[16],轴系不确定性参数和必要的确定性参数分别如表1和表2所示。这里选择d= 7和r= 3可以满足多项式混沌的估计效果,对应的样本数设置为240,采用拉丁超立方抽样确定样本。
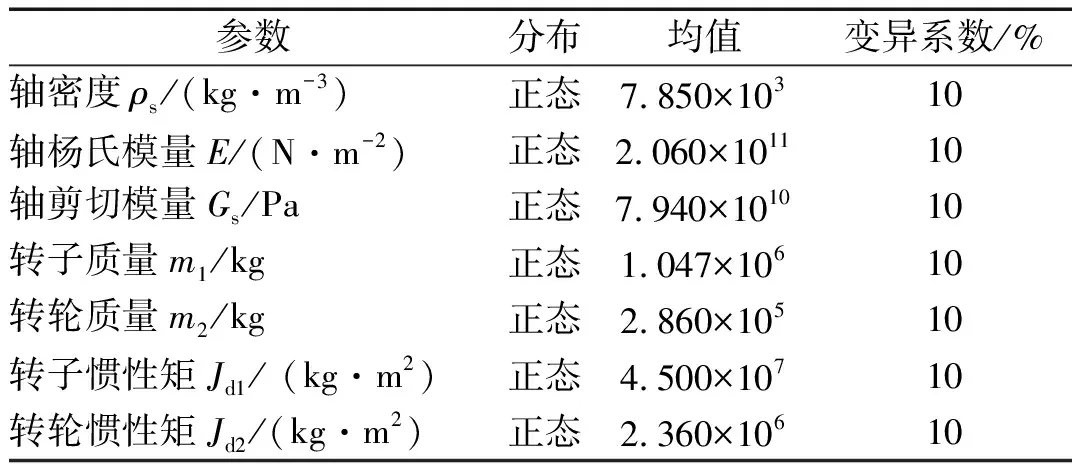
表1 不确定结构参数及其分布

表2 确定性参数

图3 数值研究流程图
4.1 验 证
随机选择120个样本,对比原始模型和代理模型下机组的振动响应来验证多项式混沌展开代理模型的准确性,对比结果如图4所示。从图4可知,多项式混沌展开模型可以很好地反映原始模型中不确定参数与随机输出的关系。

(a)转子
4.2 对固有频率的不确定性量化和参数敏感性分析
基于暴力Monte-Carlo模拟和最大熵原理计算的机组轴系固有频率的概率密度分布如图5所示。从图5可知,两种方法下的概率分布是高度一致的。但其中暴力Monte-Carlo模拟是基于10 000个样本,而最大熵原理仅仅基于240个样本。换句话说,多项式混沌展开驱动的最大熵原理方法可以在大大缩减计算量的情况下有效地评估不确定参数影响下水力发电机组固有频率的概率分布特性,且能给出连续的概率密度函数表达式,具体的表达式系数如表3所示。

(a)一阶固有频率

表3 固有频率的概率密度函数系数
基于固有频率的概率密度函数,可以得到如下结果:
(1)比较确定性框架下的固有频率响应值(determinate value, DV)和不确定性框架下的均值(mean value, MV),可以发现它们在一阶固有频率下的响应值非常接近。对比三阶固有频率,它们之间的差异被放大。而对比五阶固有频率,这种差异比一阶和三阶固有频率的差异更明显。对于高阶固有频率,其值在不确定系统中更容易偏离确定性系统的固有频率值。
(2)根据计算的概率密度函数,可以得出一阶、三阶和五阶固有频率在95%置信区间下的输出响应范围分别为[14.733 8,18.368 9],[45.584 3,55.673 3]和[88.123 7,107.056 8]。由于充分考虑了结构的不确定性,这些范围对机组的设计优化比确定的值更有意义。
(3)根据各固有频率的多项式混沌表达式,经过简单后处理,得到各固有频率的方差值分别为0.850 3,6.625 1和23.196 3,随着固有频率阶数地增加而增大。换句话说,结构不确定性对高阶固有频率的影响更为显著。
下面将利用全局敏感性分析来研究每个结构参数对固有频率不确定性的具体贡献。各参数对转轴固有频率敏感性的主效应和总效应指标在广义多项式混沌方法和传统暴力Monte-Carlo模拟下被分别提出,对比发现当基于广义多项式混沌方法计算敏感性指标时在更小的计算成本下得到的精度结果与使用大量样本的暴力Monte-Carlo模拟相同,如图6所示。
基于图6,一些关于固有频率参数敏感性的结论可以被得到:首先,一阶固有频率对参数E和Jd1是最为敏感的,也就是说,一阶固有频率的不确定性主要来源于这两个参数;同时,m2对一阶固有频率也有轻微的影响,而其他不确定参数的影响可以忽略不计。各参数对一阶固有频率的总效应指标与主效应指标非常接近,即各参数与其他参数的交互效应对一阶固有频率的影响不显著。其次,对于三阶固有频率,参数E仍然是最主要的不确定性来源,参数Jd2,ρs和Gs次之。而参数m1,m2和Jd1对三阶固有频率不确定性的贡献接近于零。此外,对于五阶固有频率,有3个显著的灵敏度参数:ρs,E和Gs,其中参数ρs对五阶固有频率的影响最为显著,而参数m1,m2和Jd2对五阶固有频率不敏感。最后,从整体的角度来说,无论是一阶、三阶还是五阶固有频率,参数E对它们的不确定性的贡献都是比较明显的。

(a)一阶固有频率
4.3 对振动响应的不确定性量化和参数敏感性分析
水力发电机组作为一种旋转机械,其振动响应也是实际工程中评价其运行状态的重要指标。因此,本节将继续基于不确定性量化和参数全局敏感性分析过程研究结构参数不确定对振动响应的影响。各个导轴承和联轴器处随机振动响应的概率分布,如图7所示。基于最大熵原理的概率密度函数表达式系数,如表4所示。通过对比可以发现在暴力Monte-Carlo模拟和最大熵原理下的振动响应概率分布是一致的。

表4 振动响应的概率密度函数系数
根据图7中机组不同位置振动响应的随机分布可知,无论在什么位置,不确定框架下的振动响应均值都非常接近于确定系统的响应值。即确定性模型可以有效地描述不确定性框架下振动响应的均值信息。同时,在最大概率下,联轴器和水导轴承处的振动响应值会明显偏离均值,而在上导轴承和下导轴承处,这一现象并不明显。其次,考虑95%的置信区间,可以得到轴系不同位置处随机振动响应的范围,分别为[4.562×10-5,7.820×10-5],[2.736×10-5,4.668×10-5],[3.054×10-5, 6.286×10-5]和[3.765×10-5,8.047×10-5]对应于上导轴承、下导轴承、耦合器和水导轴承,覆盖长度分别为3.257×10-5,1.932×10-5,3.231×10-5,4.281×10-5。另外,不同位置处随机振动响应的方差值分别为6.947 3×10-11,2.448 3×10-11,6.754 5×10-11和1.182 0×10-10。结合随机振动响应的覆盖长度和方差值,可以得到不同位置处的不确定度排序为:水导轴承>上导轴承>联轴器>下导轴承。
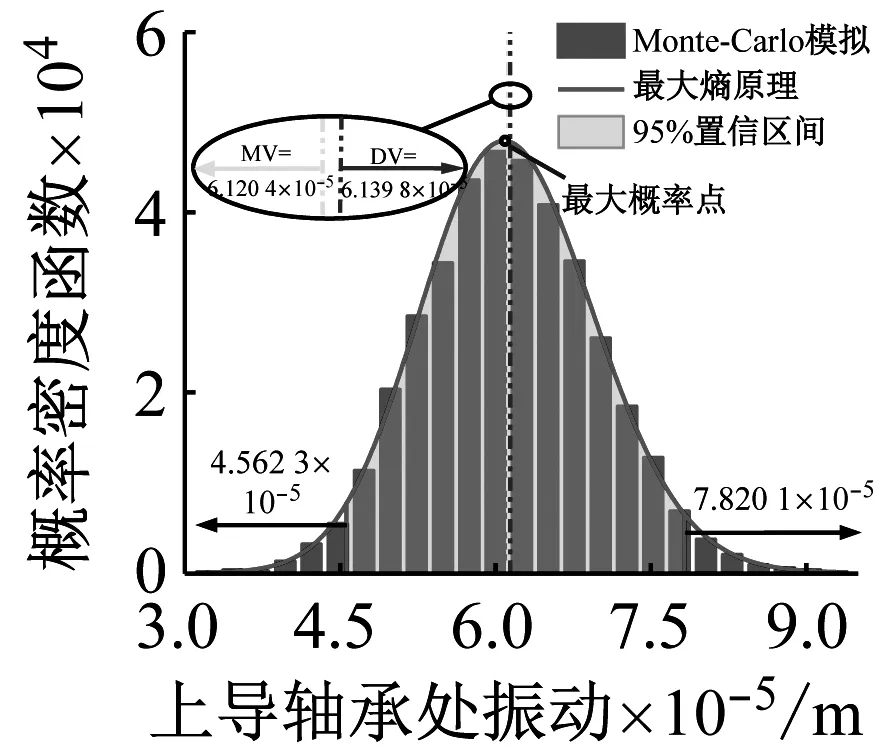
(a)上导轴承
在完成振动响应的不确定性量化分析后,下面将通过全局敏感性分析确定各不确定参数对振动响应不确定性的贡献。不同位置处振动响应的全局灵敏度指标,如图8所示,其中包括主效应指数和总效应指数。对比两种方法的结果,基于多项式混沌方法计算振动响应敏感性指标的可靠性同样得到了验证。
根据图8中关于振动响应的全局灵敏度分析,可以得到:
(1)对于振动响应而言,无论在什么位置,各不确定结构参数的主效应指标都非常接近于总效应指标,即不确定结构参数对振动响应的交互影响不明显,这与固有频率的敏感性特性是相似的。
(2)不同位置下不确定参数的敏感性指标存在明显差异。具体来说,对于上导轴承处的振动响应,最敏感的参数是m1,其次是E和Gs,最小的参数是ρs,m1,Jd1和Jd2,其中Jd1和Jd2的影响可以忽略不计。与上导轴承处的敏感性特性相比,参数m1对下导轴承处振动不确定性的贡献明显减小,而参数E和Gs的影响明显增大。此外,联轴器与水导轴承处振动响应的灵敏度指标相似,可以排序为E>m2>Gs>ρs>其他。
(3)在4.2节中,得到参数Jd1和Jd2对固有频率有明显的贡献。但从图8可以看出,参数Jd1和Jd2在任何位置对振动响应的影响都不显著或可以忽略。这表明结构参数对固有频率(静态指标)的敏感性与对振动响应(动态指标)的敏感性并不直接相关。

(a)上导轴承
5 结 论
本文提出了一种基于广义多项式混沌方法对水力发电机组轴系进行不确定性量化和全局敏感性分析的统一框架,并通过与暴力Monte-Carlo模拟结果的对比分析,验证了其可靠性。以此为基础,考虑结构参数的不确定性,对机组固有频率和振动响应的不确定性和参数全局敏感性特性进行了分析,得到了如下的主要结论:
(1)得到了结构参数不确定下机组轴系固有频率和振动响应概率密度函数的具体表达式、均值、方差和置信区间。
(2)结构参数不确定性对不同输出的传播特性表现出明显差异。在相同的不确定输入下,五阶固有频率比一阶和三阶固有频率具有更大的不确定性,而不同位置下机组振动响应的不确定度表现为——水导轴承>上导轴承>联轴器>下导轴承。
(3)参数对固有频率(静态指标)和振动响应(动态指标)的灵敏度特征不直接相关。例如,参数Jd1和Jd2只影响固有频率,而不影响振动响应。同时,各阶固有频率对参数的灵敏度也没有直接关系。
(4)参数E无论对各阶固有频率还是不同位置下的振动响应都保持较强的灵敏度,在实际工程应用中需要重点关注。
由于考虑了结构参数的不确定性,上述结果比基于确定性模型的结论对机组的设计、优化、运行和维护更有指导意义。同时,所提出的不确定性量化和全局敏感性分析框架也可以推广到水力发电机组其他不确定参数的分析研究当中。当然,本文主要是针对结构参数的不确定性展开研究,而没有考虑其他参数不确定性的影响,在后续的工作中可以进一步讨论其他类型不确定性参数对机组响应的影响效应。

