共固化阻尼薄膜夹嵌复合材料梁的振动分析

杨功先，梁 森，王光和，闫云鹏，郑长升

(青岛理工大学 机械与汽车工程学院，山东 青岛 266520)

嵌入式共固化复合材料阻尼结构(embedded cocuring composite damping structure，ECCDS)是一种多相固体，由不同性质的3种材料(树脂、玻璃纤维和黏弹性阻尼材料)通过物理或化学方法复合而成[1-3]。共固化阻尼薄膜夹嵌复合材料梁结构(co-cured damping film sandwiched composite beam structure，CDFSCBS)不仅质量轻、承载强，阻尼性能优良，且更加耐疲劳，减振降噪，在航空、航海与陆地承载等交通运输领域有广泛的应用前景。

Zhai等[4-5]基于1阶剪切变形理论，探讨了在阻尼薄膜复合材料结构中改变黏弹性层参数对结构动力学性能的影响，为其优化结构提供了理论依据。黄志诚等[6]建立了一种新的用于研究黏弹性夹芯梁振动和阻尼特性的有限元模型，该模型同时考虑了黏弹性层的剪切和压缩阻尼。Filippi等[7]提出了基于Carrera统一公式改进的梁理论的有限元模型，用于夹层梁的振动分析。Nguyen等[8]基于增强型高阶分析理论研究了功能梯度夹层板的弯曲、振动及屈曲特性。Jin等[9]基于 Reddy理论分析了单层黏弹性夹层梁的阻尼及振动特性。

Yu等[10]提出了分段剪切变形理论及假设，创建了夹层梁结构的理论模型，并研究了夹层梁在两端固支边界条件下的自由振动与热后屈曲问题。肖龙江等[11]研究了两端固支边界条件下具有小初始挠度的屈曲梁在受到基础简谐激励作用时的非线性动力响应。钟阳等[12]根据辛几何方法对哈密顿体系下的四边固支矩形薄板的自由振动进行了求解，并得到精确解。张小广等[13]对四边固支功能梯度矩形板在受到横向简谐激励力作用时的非线性主共振问题进行了研究。鲍四元等[14]根据非局部理论，将旋转约束、横向位移弹簧引入到梁结构两端边界上，并通过设置其刚度的大小来模拟固支边界条件，得到了梁的固有频率和阵型曲线。郝芹等[15]根据波传播法对两端固支梁在轴向运动时的横向自由振动进行了分析，得到了梁的模态函数和固有频率。Ding等[16]构造了一个包含未知系数的应力函数，通过Airy应力函数方法得到了应力与位移的一般表达式，并利用两端固支边界条件确定引入应力函数的未知系数，最终得到了两端固支各向同性材料梁的解析解。

虽然目前国内外很多学者对复合材料层合板、梁结构的振动研究较多，且获得的成果颇丰。但大多数研究集中在无阻尼、自由阻尼或约束阻尼结构，鲜有文献对共固化阻尼薄膜夹嵌复合材料固支梁结构动力学性能的研究报道。因此本文基于Hamilton原理、1阶剪切变形理论与变分原理，推导出CDFSCBS的应变能、动能以及该结构动力学微分控制方程的表达式，探索出满足两端固支边界条件的位移函数，利用伽辽金加权余值法将CDFSCBS自由振动的偏微分方程转化为一个齐次线性方程组，从而获得模型的理论解。运用ANSYS软件创建阻尼薄膜梁有限元模型，同时制作CDFSCBS试件和所搭建的试验平台，进行数值模拟与模态试验，将模拟结果、试验结果分别与理论解对比，验证了理论模型的有效性。在此基础上进一步探讨了阻尼层厚度，上下约束层的比例，以及结构几何参数对CDFSCBS的动力学性能的影响。

1 基本方程

1.1 基本假设

共固化阻尼薄膜复合材料梁的几何结构及尺寸，如图1所示。其面内位移如图2所示。为了得到结构的振动方程，做出如下假设：

图1 CDFSCBS的几何结构

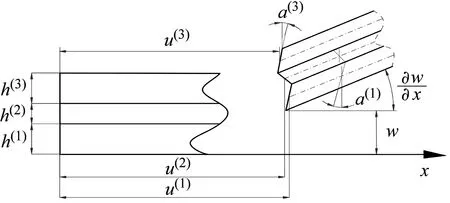
图2 CDFSCBS的面内位移

(1)嵌入的阻尼层与复合材料层之间的黏结良好，层间变形连续，振动过程中不发生滑移。

(2)结构变形前后，垂直梁面的同一法线上的各点沿厚度方向的位移变化忽略不计。

由于梁结构的跨度远大于它的宽度和厚度，因此在理论计算中通常将其简化为一维结构进行理论建模，得到的方程不仅简单且计算效率较高，接下来对CDFSCBS进行详细的理论推导。

1.2 阻尼薄膜复合材料梁的本构关系

本文采用考虑剪切变形的铁木辛柯梁理论，结合所做假设，各层梁的位移模型如下

(1)

z(i)的意义如图3所示。在每一层建立独立的坐标系，并将坐标系的原点设置在每一层的中心线上，因此z方向坐标z(i)的取值范围为(-hi/2,hi/2)。

图3 z(i)的几何意义

根据式(1)可得第i层梁结构的位移-应变关系表示如下

(2)

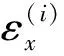
(3)

式中，θi为纤维方向与x轴的夹角。

由于黏弹性阻尼层的损耗因子与复合材料层损耗因子相比较大，为计算方便将复合材料层阻尼忽略不计，故实际损耗因子会略高于计算得到的整体损耗因子，因此只对黏弹性阻尼层的剪切模量与弹性模量用常复数模量表示

(4)

式中，n为阻尼层，n=2。

1.3 阻尼薄膜复合材料梁结构的振动方程

对CDFSCBS振动方程的推导过程如下，基于Hamilton变分原理[17]有

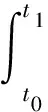
(5)

其中，应变能和动能的表达式如下

(6)

(7)

根据假设(1)，可知中间层的位移为

(8)

这样可将变量减少到5个，分别是u1,u3,α1,α3和w。

将式(6)和式(7)代入式(5)，结合式(2)、式(3)和式(8)，整理可得阻尼薄膜复合材料梁结构的振动方程，如下

δu1：

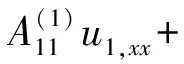
(9)

δu3：

(10)

δw：

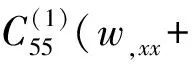
(11)

δα1：

(12)

δα3：

(13)

其中

两端固支阻尼薄膜复合材料梁的边界条件为

(14)

方程的解可以展开成以下振型函数叠加的形式

(15)

式中，ω*为圆频率；U1，U3，W，Ø1和Ø3为系数。

对于两端固支边界条件，振型函数可以采用以下形式

(16)

将式(15)、式(16)代入式(9)～式(13)，并将其展开成以下三角级数叠加的形式

(17)

由伽辽金加权余值的思想可知，三角级数系数应满足

(18)

根据式(17)与式(18)，可将平衡方程转化为如下特征值问题

KX=M(ω*)X

(19)

式中：K为整体刚度矩阵；M为整体质量矩阵；X=(U1,U3,W, Ø1, Ø3)T。

由式(19)、式(20)与式(21)(见文献[18])计算结构的振动频率和损耗因子

(20)

η=Im((ω*)2/Re(ω*)2

(21)

2 试验平台的搭建与模型验证

2.1 试验平台的搭建

按照碳纤维/环氧预浸料固化工艺曲线制成阻尼薄膜复合材料梁试件，如图4所示。具体制备工艺参见文献[19],该试件的几何参数与材料参数，如表1、表2所示。搭建试验平台，如图5所示。将制作完成的CDFSCBS试件进行模态试验，试验平台包括激励力锤(型号4524-B004)、加速度传感器(型号8206-002)、固支夹具、计算机和PULSE(型号3560B)。将3个相同的CDFSCBS试件分别进行试验，试验采用单点激励多点响应的方法对两端固支CDFSCBS进行模态参数识别，3次激励数值取平均，3次试验数据再次取平均，以便获得较准确的试验结果。

表1 CDFSCBS复合材料层材料参数

表2 CDFSCBS黏弹性层材料参数

图4 阻尼薄膜复合材料梁试件

(a)

2.2 模型验证

以无阻尼复合材料层合梁为例，验证所创建理论模型的有效性。其材料参数为：ρ=1 389.23 kg/m3,E1=144.8 GPa,E2=9.65 GPa，G12=4.14 GPa,G13=4.14 GPa,泊松比v12=0.3；层合梁结构的尺寸为：a=0.381 m，h=a/15；每一层纤维角度为[90°/0°/90°/0°]。表3列出了采用本文方法计算得到的前3阶固有频率与现有文献数据对比，可以看到良好的一致性。

表3 固支边界条件下复合材料层合梁前3阶固有频率对比

此外，将ANSYS有限元方法、模态试验方法分别与理论分析方法进行比较。运用ANSYS17.0软件的Solid Brick 8 node 185单元建立阻尼薄膜复合材料梁模型，各层之间通过共节点连接，设置每一铺层厚度、铺设角度、材料参数，具体见表1与表2。

CDFSCBS的损耗因子与前3阶固有频率的理论、试验、模拟结果对比如表4所示。三者结果基本吻合，误差均在5%以内，满足工程应用中需要。其中，误差1为理论解与ANSYS模拟结果的相对误差，误差2为理论解与试验结果的相对误差。

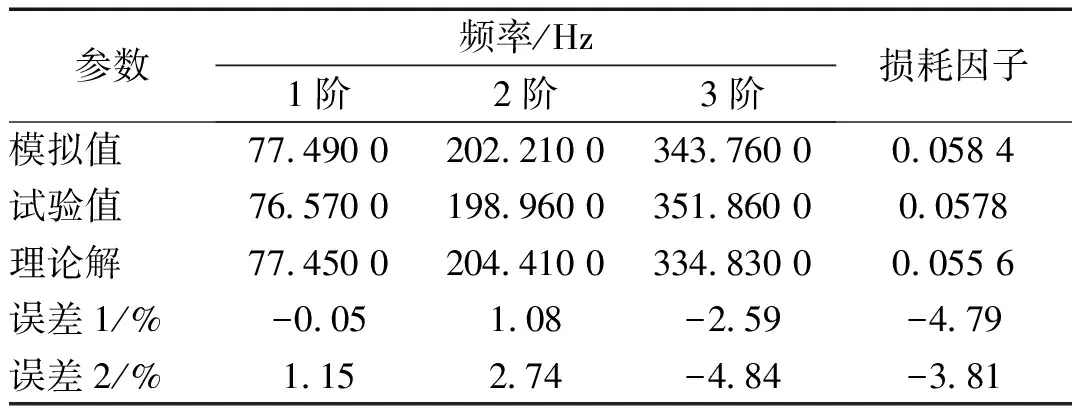
表4 固有频率和损耗因子计算结果

3 不同参数对CDFSCBS动力学性能影响

在验证了理论模型正确的基础上，进一步探讨了结构的阻尼层厚度，上下复合材料层比例，阻尼层厚度(Hc)与CDFSCBS的总厚度(H)比，CDFSCBS长度(a)与CDFSCBS的总厚度比对CDFSCBS整体动力学性能的影响。令H=h1+h2+h3，Hc=h2，材料参数见表3。

3.1 结构材料分布对动力学性能的影响

当CDFSCBS上下复合材料层厚度h1+h3=2 mm时，改变黏弹性阻尼层厚度h2的数值，探讨h1/h3以及黏弹性阻尼层厚度变化对CDFSCBS的1阶频率与1阶模态损耗因子的影响规律，结果如图6与图7所示。

图6 h2不同时h1/h3值对CDFSCBS 1阶频率的影响

h1+h3为定值时，在h1/h3=1处出现1阶频率的极小值点和1阶损耗因子极大值点，改变阻尼层厚度h2的值，极值点位置不变。这是因为当阻尼层处于中性层位置时，CDFSCBS在纯弯曲情况下，中性层受到的剪切应力最大，阻尼层可以获得较大的应变，由模态应变能原理可知，此时CDFSCBS具有最大的1阶损耗因子与相对最小的1阶频率。

当CDFSCBS的上下复合材料层相等时(h1/h3=1)，保持其他材料参数不变，增加阻尼层厚度，CDFSCBS的1阶频率降低，1阶模态损耗因子则有较大增加(见图6与图7)；当CDFSCBS上下复合材料层不相等时(h1/h3≠1)，增加阻尼层厚度，CDFSCBS的1阶频率与1阶模态损耗因子都呈增加趋势，但变化幅度不大。这是因为随着阻尼层厚度增加，CDFSCBS的整体阻尼性能得到了提升。又因阻尼层在CDFSCBS中的位置不同，增加其厚度对阻尼性能的提升效果也存在差异，因此阻尼层位于中性层位置更有助于提升CDFSCBS整体的动力学性能。

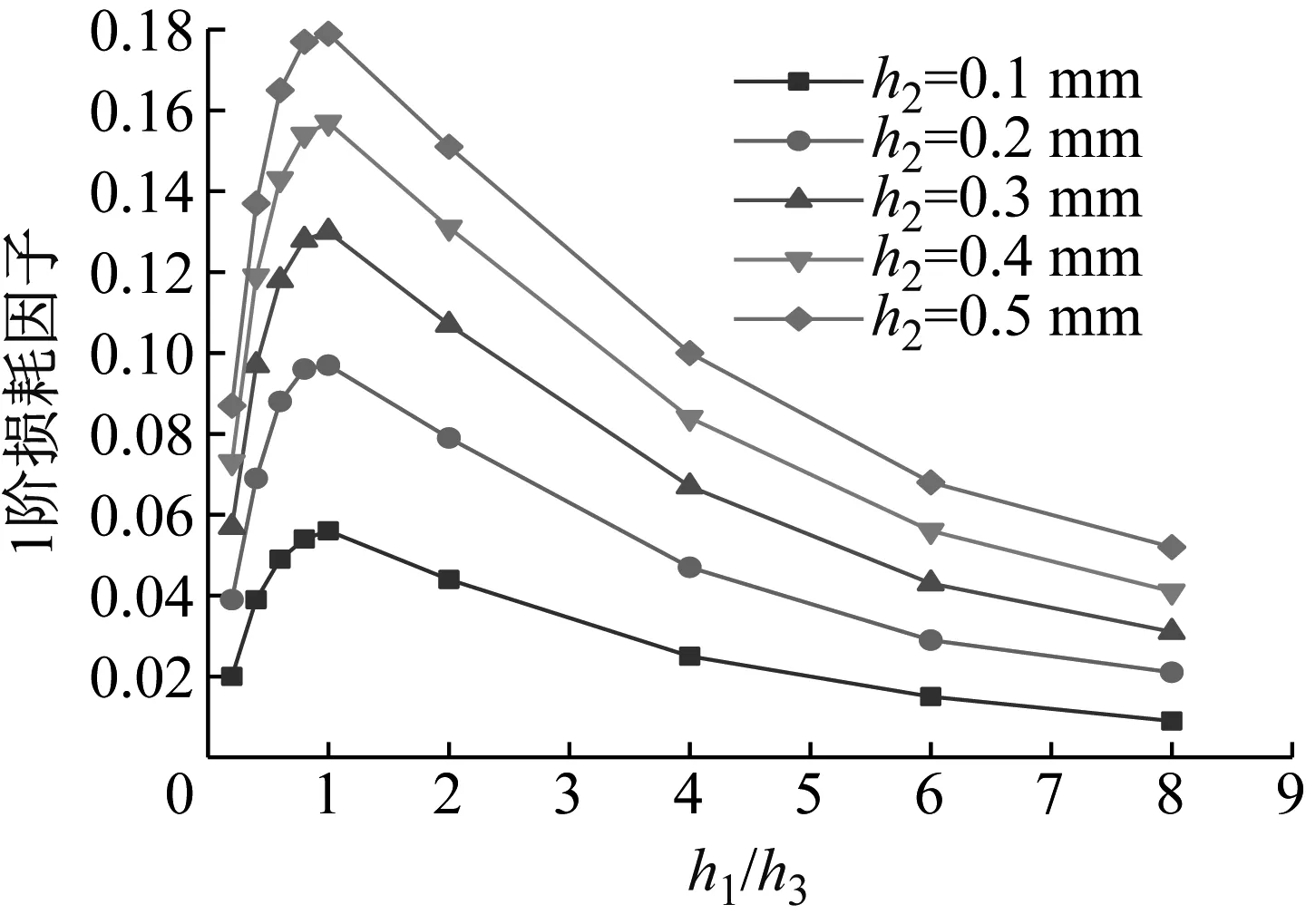
图7 h2不同时h1/h3值对CDFSCBS 1阶损耗因子的影响

3.2 结构几何参数对动力学性能的影响

增加CDFSCBS的阻尼层厚度可提升其阻尼性能，因此基于阻尼薄膜梁在总厚度不变的情况下，探讨黏弹性阻尼层厚度与总厚度的比(Hc/H)和梁长度与总厚度的比(a/H)对CDFSCBS动力学性能的综合影响规律，结果如图8～图23所示。

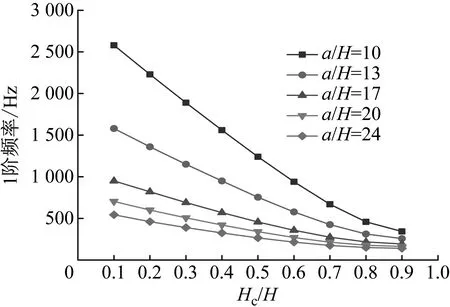
图8 Hc/H与a/H对CDFSCBS 1阶频率的影响

图9 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

图10 Hc/H与a/H对CDFSCBS 1阶频率的影响

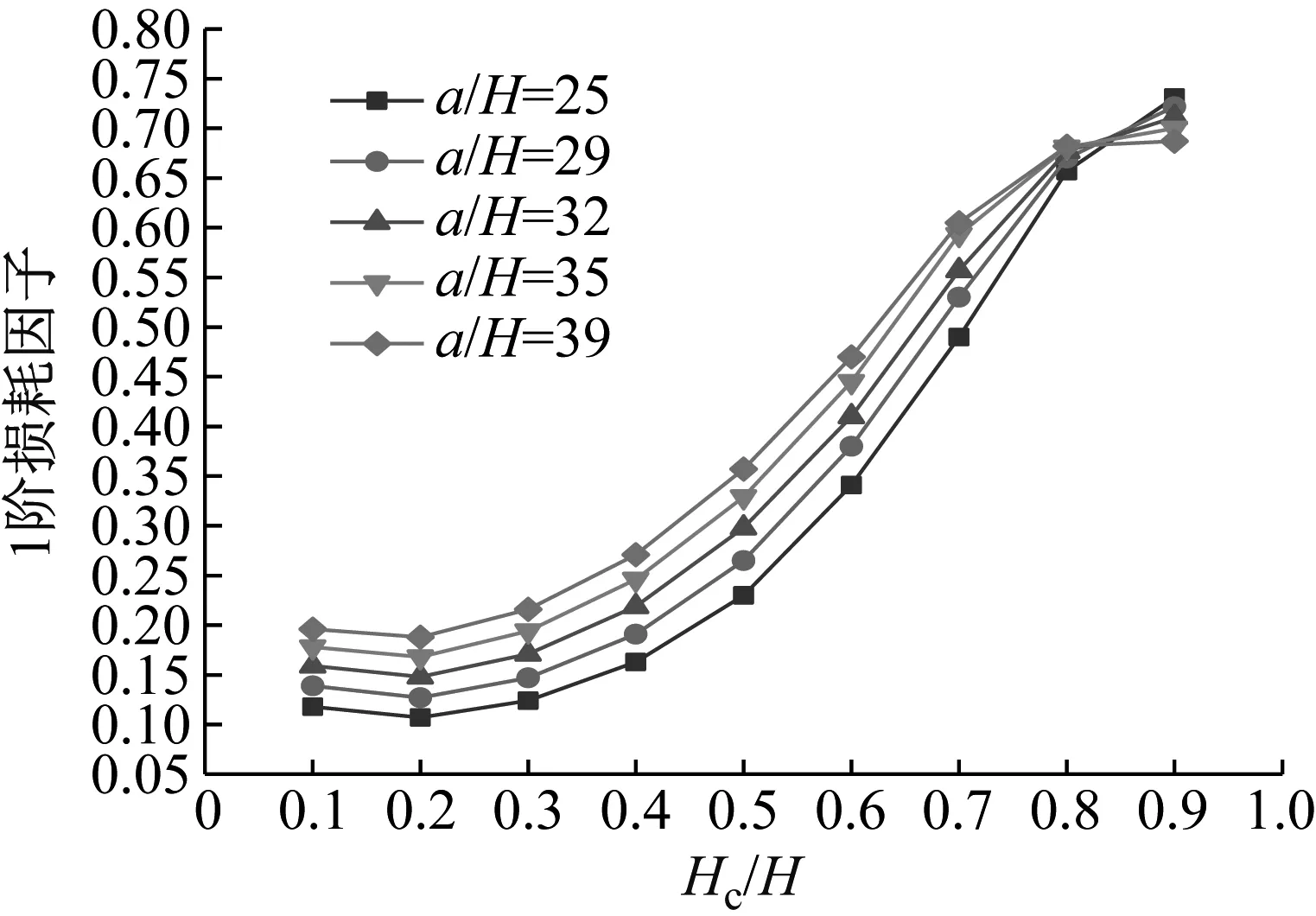
图11 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

图12 Hc/H与a/H对CDFSCBS 1阶频率的影响

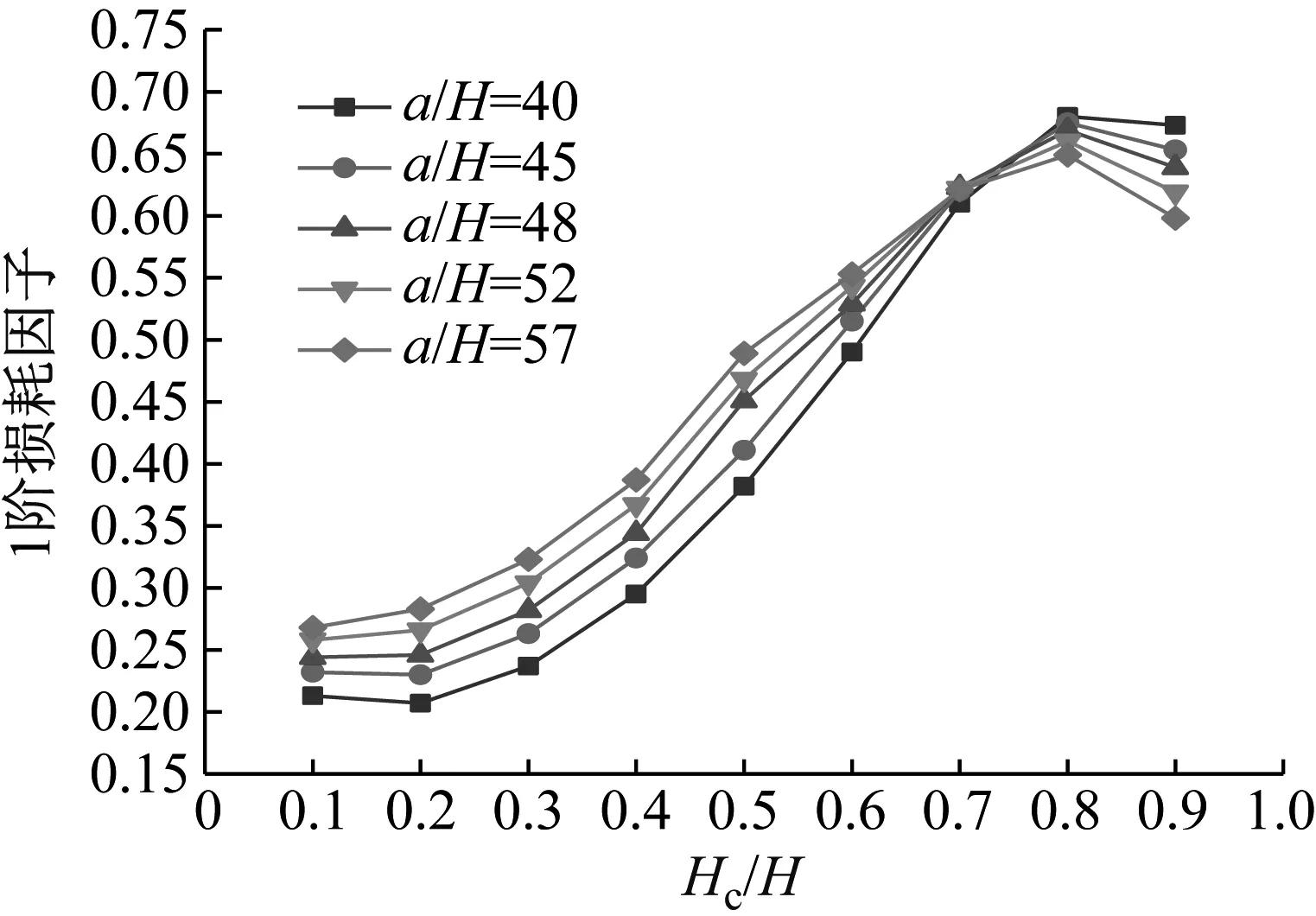
图13 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

图14 Hc/H与a/H对CDFSCBS 1阶频率的影响

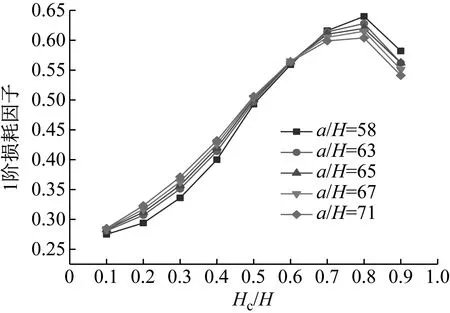
图15 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

图16 Hc/H与a/H对CDFSCBS 1阶频率的影响

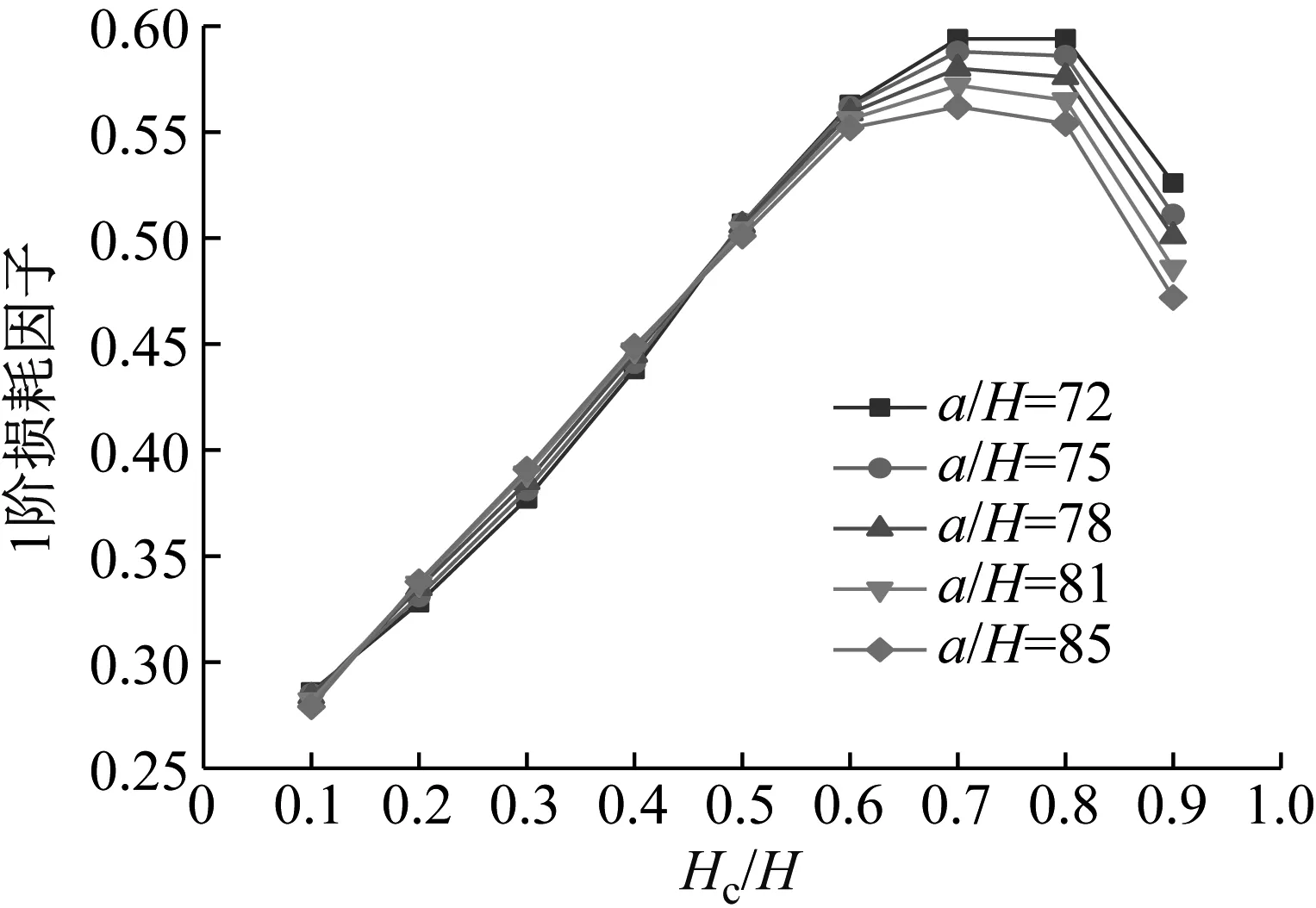
图17 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

图18 Hc/H与a/H对CDFSCBS 1阶频率的影响

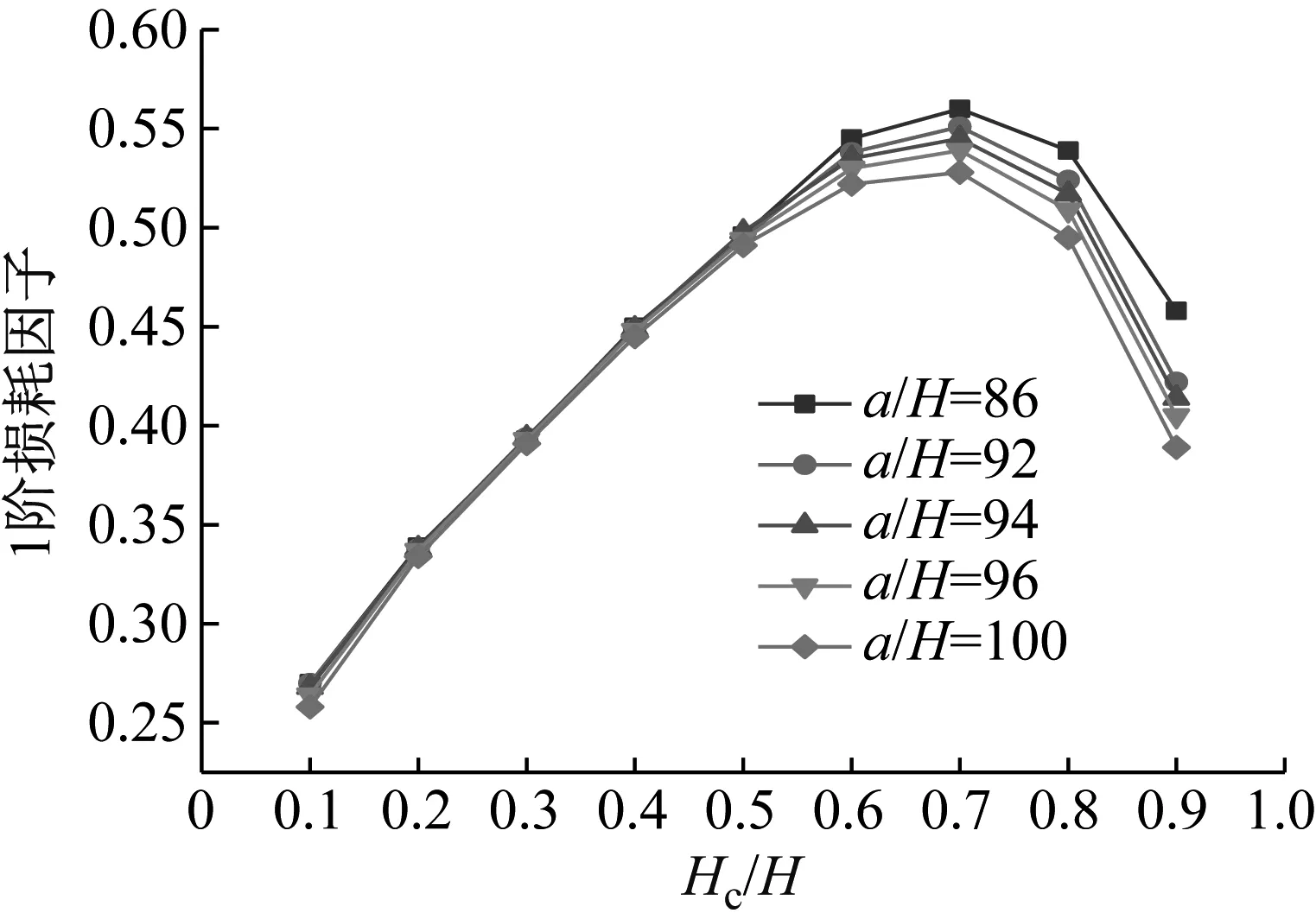
图19 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

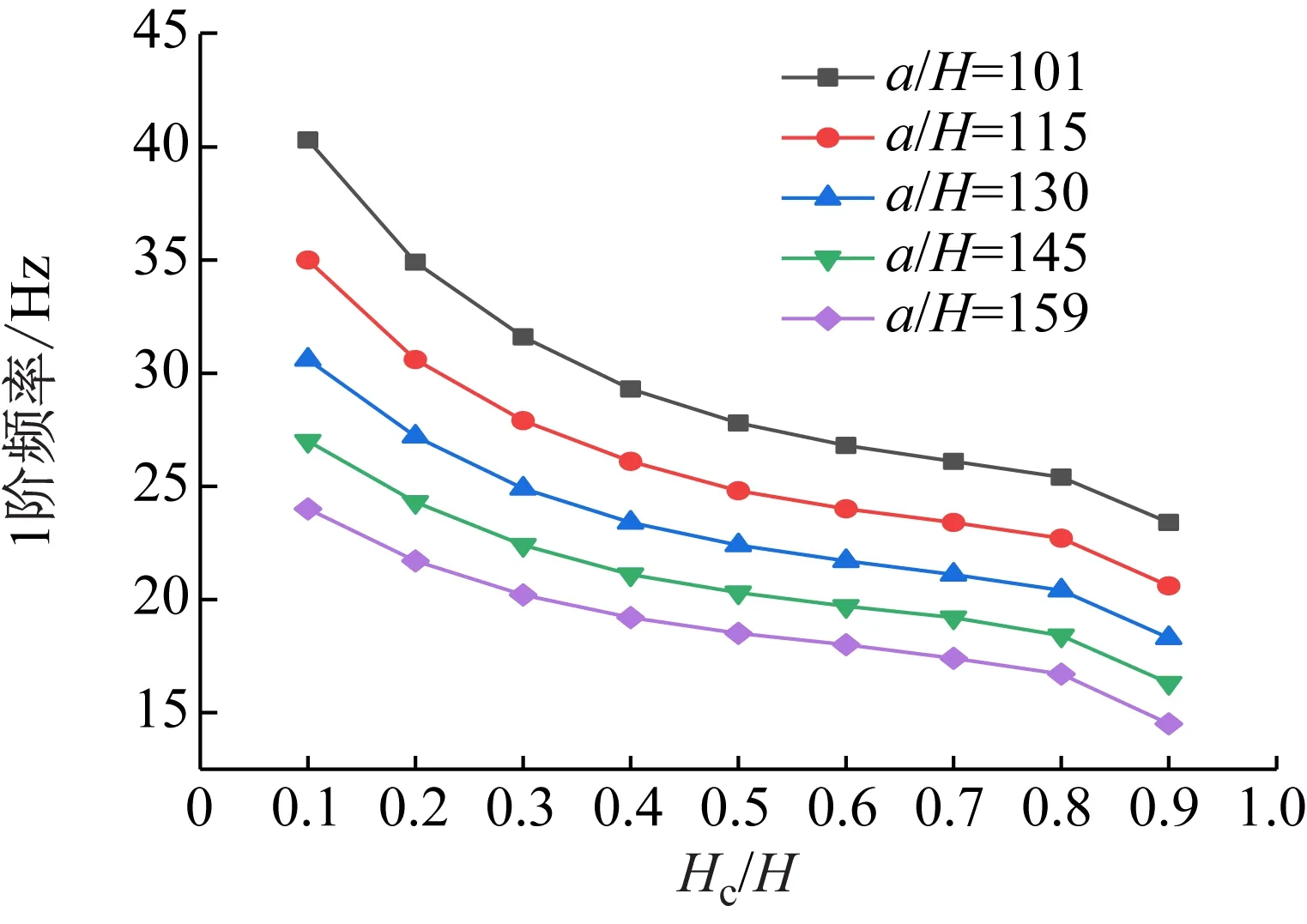
图20 Hc/H与a/H对CDFSCBS 1阶频率的影响

图21 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

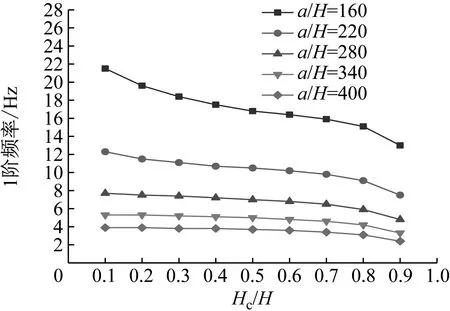
图22 Hc/H与a/H对CDFSCBS 1阶频率的影响

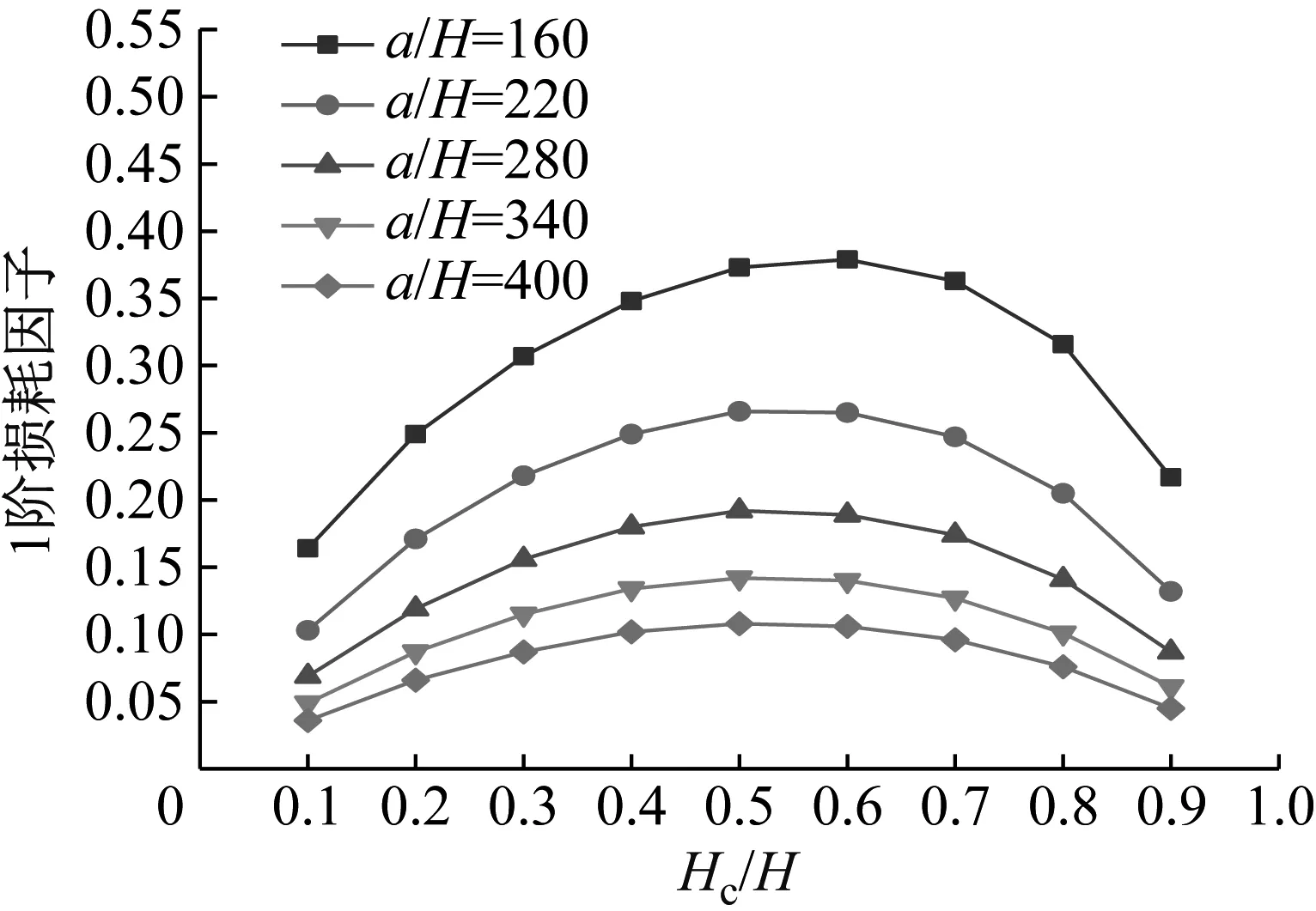
图23 Hc/H与a/H对CDFSCBS 1阶损耗因子的影响

由图8～图11可知，随着a/H与Hc/H值的增加，CDFSCBS的1阶频率呈下降趋势；1阶模态损耗因子整体呈上升趋势，这是因为a/H在10～39内，随着Hc/H值的增加，CDFSCBS的阻尼性能一直在提升。因此当a/H在10～39内，CDFSCBS的损耗因子达到最大值时所对应的Hc/H值约为0.9，此时CDFSCBS拥有更好的动力学性能。

由图12～图23可知随着a/H与Hc/H值的增加，CDFSCBS 1阶频率的变化趋势与图8～图11类似呈逐渐下降趋势，1阶模态损耗因子则呈先上升后下降趋势。在总厚度不变情况下，长厚比不同，损耗因子达到最大值、结构获得最佳动力学性能所对应的Hc/H值也各有不同。即a/H值约为40～71，对应的Hc/H值约为0.8；a/H值约为72～100，对应的Hc/H值约为0.7；a/H值约为101～159，对应的Hc/H值约为0.6；当a/H值大于160时，对应的Hc/H值约为0.5。

4 结 论

本文基于Hamilton原理与1阶剪切变形理论，推导了CDFSCBS的自由振动理论模型，利用伽辽金法求解了模型的理论解。在验证了理论模型有效性的基础上，进一步探讨了CDFSCBS结构材料分布、几何参数对CDFSCBS的动力学性能的影响规律。主要结论如下：

(1)当阻尼层位于结构的中性层位置，上下复合材料层关于其对称分布时，CDFSCBS具有相对最低的1阶频率与最大的模态损耗因子；

(2)通过合理选择最佳的a/H与Hc/H值，可得到最大的1阶模态损耗因子，提升CDFSCBS整体的动力学性能；

(3)分析并得出了Hc/H与a/H之间的最优关系——随着a/H值的增大，最大损耗因子所对应的Hc/H值约为0.5。