时空相关的短时交通流宽度学习预测模型

罗向龙，郭 凰，廖 聪，韩 静，王立新

1.长安大学 信息工程学院，西安710064

2.中铁第一勘察设计院集团有限公司，西安710043

随着我国经济的快速增长，交通基础设施建设的步伐越来越快，但是公路里程的增加很难满足汽车增长速度和人们的出行需求，导致道路交通堵塞问题日益严重。智能运输系统（intelligent transportation systems，ITS）成为全世界所公认的解决交通拥堵问题的有效手段。短时交通流预测问题是ITS研究的关键技术之一，及时准确的交通流预测可为出行者提供精准可靠的动态路径诱导，有效提高出行效率，成为国内外研究的热点[1]。

短时交通流预测模型和方法概括起来主要包括基于统计方法的模型、智能模型、组合模型三类。基于统计方法的模型主要以自回归滑动平均（autoregressive moving average，ARMA）及改进的时间序列模型为代表。王晓全等[2]利用差分自回归滑动平均（autoregressive integrated moving average，ARIMA）模型对北京城市快速路二环的交通流进行预测；李晓磊等[3]利用季节性差分自回归滑动平均（seasonal autoregressive integrated moving average，SARIMA）模型对港口船舶交通流进行预测。基于统计方法的短时交通流预测模型理论成熟，应用简单，但其主要针对线性平稳数据，对于受多种因素影响的非线性的交通流数据，其预测结果精度不高[4]。随着机器学习的迅速崛起，出现以人工神经网络[5]（artificial neural network，ANN）、支持向量机（support vector machine，SVM）等为代表的智能模型。Chen等[6]对人工蜂群（artificial bee colony，ABC）算法进行改进，改变雇佣蜜蜂搜索策略，提高全局搜索能力，进一步利用径向基函数（radial basis function，RBF）神经网络对交通流进行预测。Feng 等[7]建立自适应多内核SVM 模型，内核函数由高斯内核函数和多项式内核函数组成，依据实时输入的交通流数据变化趋势对两个内核函数的权重实时更新，利用交通流数据时空相关性实现预测。智能模型参数设置较困难，且预测结果容易陷入局部最优，从而使其应用受到限制。为了进一步提高交通流数据预测精度，越来越多的组合预测模型也出现在人们的视野中。刘剑等[8]利用核主成分分析法对输入的交通流数据预处理，利用SVM 对不同工作日的交通流进行预测。田瑞杰等[9]利用时间序列模型ARMA 和ARIMA 对路段不同时刻检测速度进行预测，进一步利用反向传播神经网络对二者预测结果加权融合，实现最终预测。Luo等[10]利用离散傅里叶变化（discrete Fourier transform，DFT）算法将交通流数据分解为共同趋势和残余分量，共同趋势由极致外推法预测，残余分量通过支持向量回归（support vector regression，SVR）模型实现预测。组合模型同样受交通数据自身特性和组合方法的影响而不具有普适性。

近年来随着深度学习[11]、大数据处理[12]等新技术的浪潮的出现，基于深度学习的交通流预测方法成为研究的热点[13]。Zhang等[14]利用一种共轭梯度算法对深度信念网络（deep belief network，DBN）的参数进行微调，利用遗传算法寻找DBN 在不同时间下的最优超参数，对改进的模型进行预测性能测试。罗文慧等[15]利用卷积神经网络（convolutional neural network，CNN）进行交通流数据特征提取，将提取特征通过SVR 实现预测。Kang等[16]将观测的流量、速度、占有率同时作为交通流量预测的输入，利用时空相关性，通过长短期记忆（long short-term memory，LSTM）循环神经网络模型进行训练，该方法克服循环神经网络（recurrent neural network，RNN）中存在的梯度消失和梯度爆炸问题，提高预测精度。Wu 等[17]利用注意力模型（attention model）决定历史交通流数据的重要程度，利用CNN 挖掘数据的空间相关性，利用RNN挖掘数据的时间特征。Luo等[18]利用KNN 计算得到与测试站点最相关的K个邻近站点，构造合适的数据集代入LTSM模型中，实现目标站点的预测。由于深层结构模型复杂，涉及到大量的超参数，网络训练过程非常耗时，很难满足交通流序列预测的实时性需求；此外，为了获得更高的精度，深层结构不断叠加层数，导致深层结构的理论分析变得非常困难。

为了克服深度学习存在的问题，2018年，陈俊龙等[19]提出了宽度学习系统（broad learning system，BLS）。宽度模型因结构简单，运算速度快，逐渐被应用到图像分类[19]、时间序列预测[20]等领域中。本文在宽度模型的基础上，利用交通流数据的时空相关性，提出了一种KNN-BLS 组合模型短时交通流预测方法。利用KNN算法筛选与预测路段时空相关性高的K个路段，选取的K个路段交通流数据作为BLS模型的输入分别进行预测，并对预测结果进行加权融合实现误差修正，以均方根误差为最小时对应K值的结果作为最终的预测值。美国加利福尼亚州交通局PeMs（performance measurement system）交通数据库实测的交通流数据的测试结果表明，提出的方法预测误差平均降低46.56%，同时运算效率提高99%以上，是一种有效的短时交通流预测方法。

1 BLS算法

宽度学习算法是一种新的机器学习算法，该算法的核心思想是将原始数据通过特征提取产生映射特征，进一步形成特征节点，并将映射特征通过广义扩展生成增强节点，依据输出与连接的特征节点和增强节点之间的连接权重，得到整个网络的输出，典型的宽度学习网络结构如图1所示。

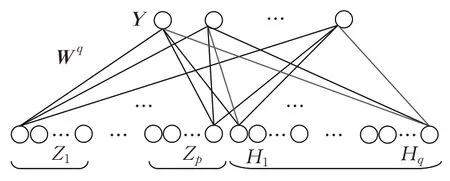
图1 宽度学习系统网络结构Fig.1 Structure of BLS model

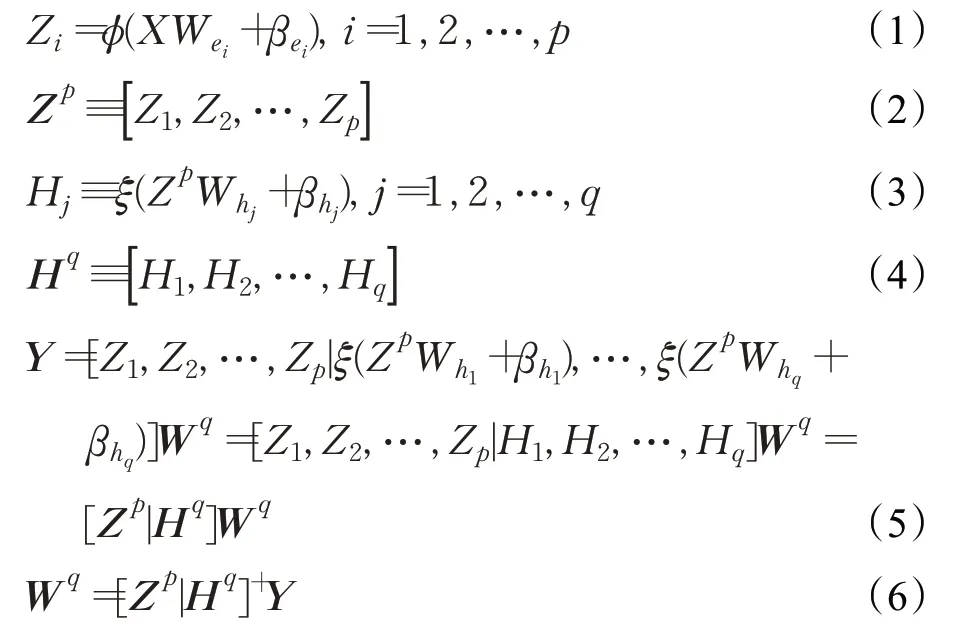
对于输入数据X，通过随机权重、偏置和激活函数ϕ映射形成第i个特征Zi，每个特征包含l个节点，共产生p个映射特征；组合所有特征形成增强节点的输入Zp，通过随机权重、偏置和激活函数ξ对其进行映射形成第j个增强节点Hj，共有q个增强节点；组合所有特征和增强节点构成模型的输入[Zp|Hq]；最后通过与输出Y之间的连接权重Wq得到网络的输出。

通过图1 可以发现，和深度学习模型相比，宽度模型不需要利用梯度下降算法进行多次迭代，而是计算输入层与输出层的伪逆，得到连接权重，进一步得到网络输出，从而有效减少了运算量。

2 KNN算法

KNN算法是一种度量空间中历史点与当前点相似程度的算法，由于它运算速度快，操作简单，广泛应用于不同研究领域。其核心思想是计算不同状态点之间的距离，找到与当前点最相近的K个历史点。常用的计算距离的方法，包括欧式距离、哈夫曼距离、马氏距离等。由于欧式距离反映的是整体相似性，本文中采用欧氏距离进行交通流数据的空间相关性的选择。

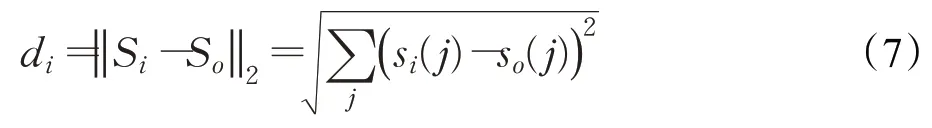
其中，Si表示第i个检测路段的交通流数据，So表示预测路段的交通流数据，si(j)和so(j)分别表示第i个检测路段和预测路段在j时刻采集到的交通流数据。

3 KNN-BLS短时交通流预测模型

假定给定的公路网包含M个断面，第m个检测路段在不同天的交通流数据表示为Sm，由于交通流数据具有很强的时间相关性，以连续D周同一天不同路段采集到的交通流量S作为测试数据，即：

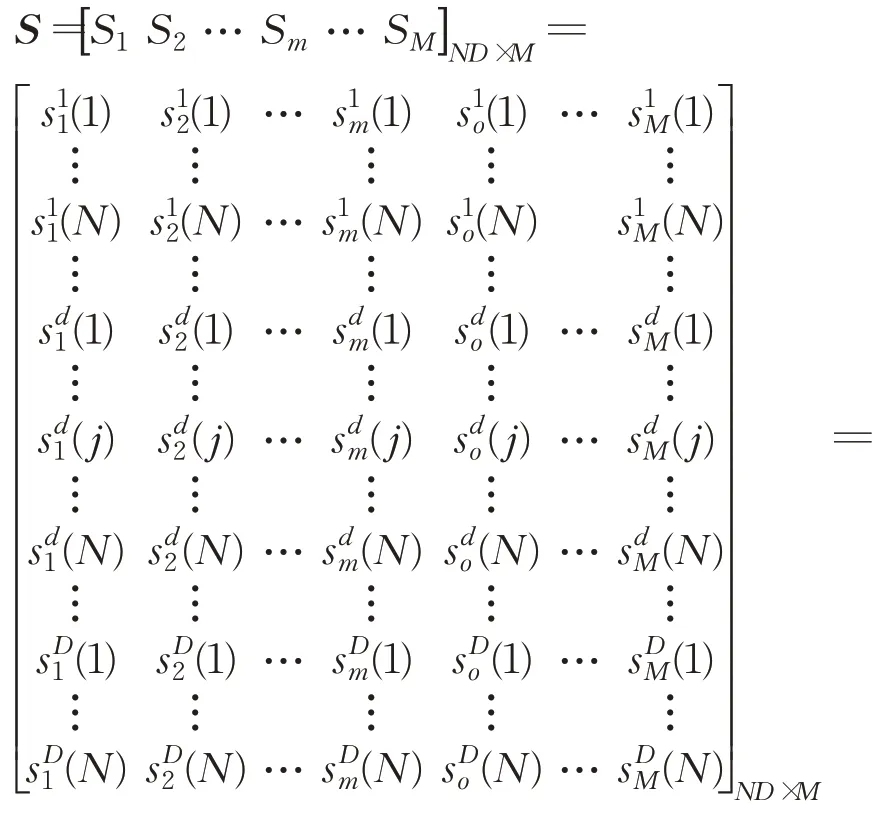
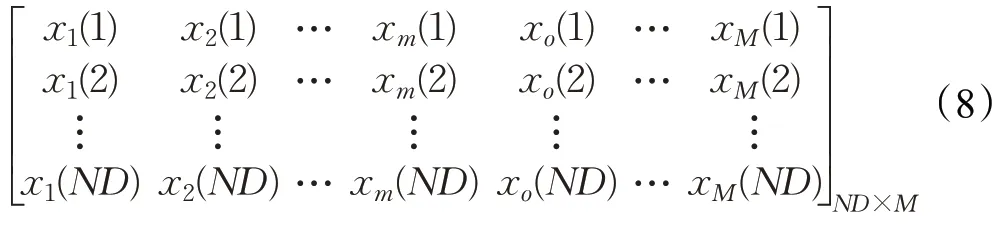
通过式（9），分别计算第m个检测路段与预测路段前D-1周交通流数据的欧氏距离dm，筛选与预测路段最相关的K组路段，分别记作Xk，其中，k=1,2,…,K。

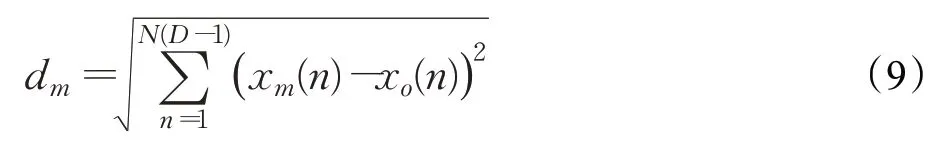
对于选择的K个路段，分别构建BLS 模型的训练输入TRk_input、输出TRk_output和测试输入Tk_input，如式（10）～（12）所示，其中，τ表示预测步长。

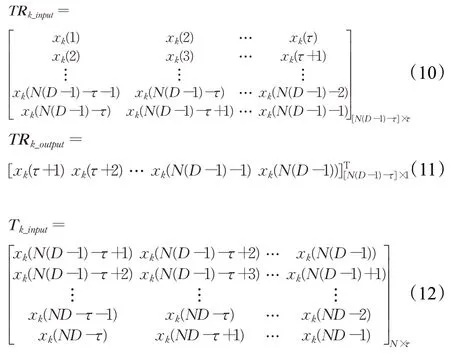
将式（10）和（11）代入式（1）～（6）中，得到连接权重Wk∈ℝ(pl+q)×1：

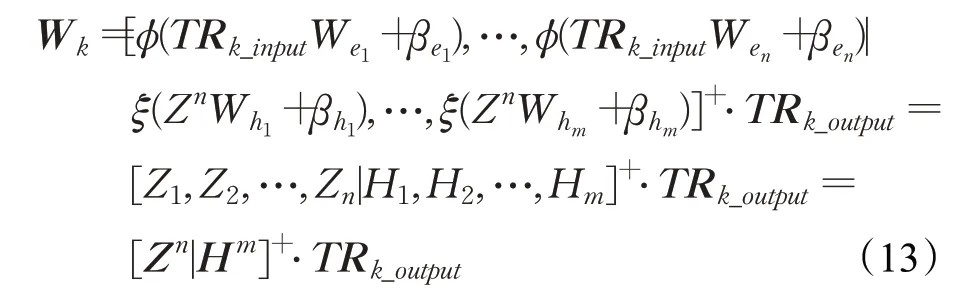
将式（12）代入式（1）～（5）中，并根据式（13）的连接权重对预测路段的交通流量分别进行预测，得到以第k个路段为输入的预测结果∈ℝN×1：

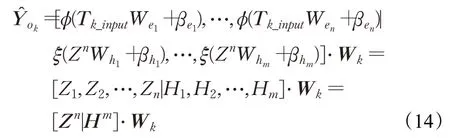
对不同的K组预测结果进行加权，以均方根误差最小时对应K值的加权值作为最终的交通流预测结果：

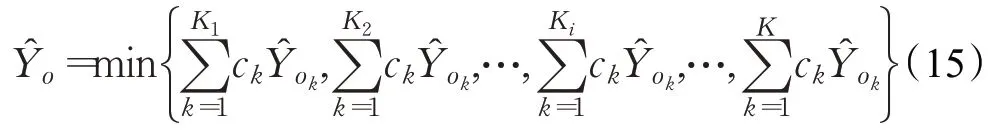
其中，加权系数ck表示第k组检测路段均方根误差的倒数占比，K1,K2,…,Ki,…,K表示选择的路段个数，且Ki≤M。

4 实验

4.1 数据来源

本文实验数据来自美国加利福尼亚州交通局PeMs（performance measurement system）交通数据库实测的交通流数据。实验中选用不同43个断面在2018年2月5 日至2018 年3 月25 日连续七周采集到的周三的交通流数据作为实验数据，将前六周数据作为训练数据，第七周数据作为测试数据，数据采样周期为5 min，即M=43，D=7，N=288。

4.2 预测结果性能评价指标

均方根误差（root mean square error，RMSE）是评价交通流预测性能最常用的指标，本文采用RMSE作为评价指标，计算公式如式（16）所示：

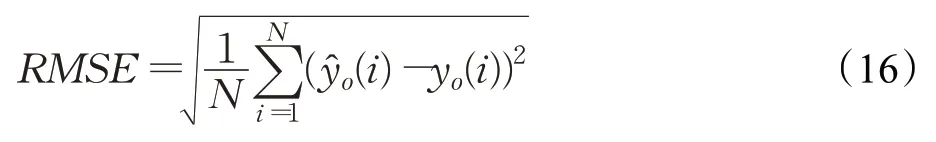
4.3 预测结果性能分析

本次实验运行环境及参数配置：电脑CPU 为2.60 GHz，内存为8.00 GB，编程语言为Python3.7。实验中经过反复测试设置BLS 模型每个特征包含节点个数l=5，映射特征共有p=6，增强节点个数q=41，激活函数为tansig，预测步长为τ=6。预测结果如图2所示，从图2中可以看出，预测结果很好地反映出交通流序列的变化趋势，尤其在早高峰和晚高峰时期，预测结果很好地反映了交通流量的波动性，表明了提出的KNN-BLS模型进行短时交通流预测的有效性。

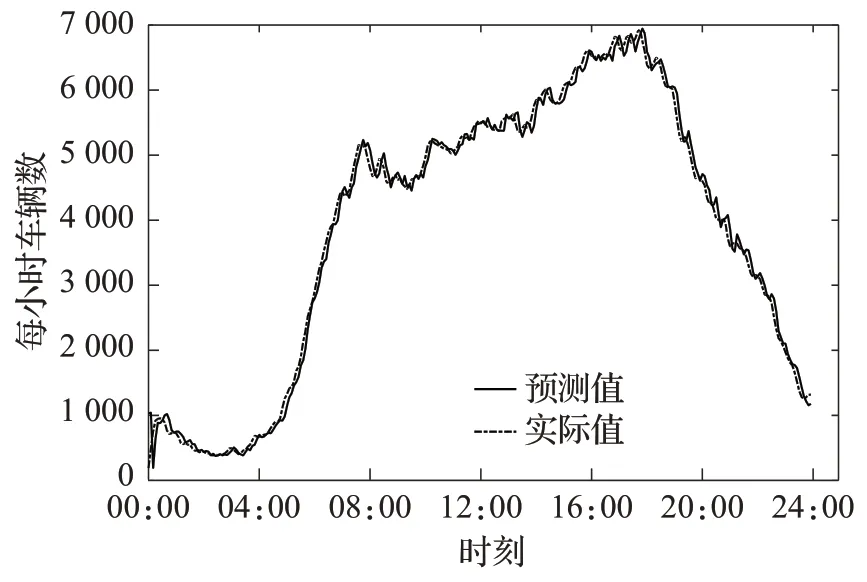
图2 预测结果和真实值Fig.2 Predicted and real traffic flow

为了进一步评价提出的KNN-BLS 模型的性能，本文与四种常见的模型ARIMA、小波神经网络（wavelet neural network，WNN）、LSTM、KNN-LSTM分别进行对比分析，不同模型参数设置如下：ARIMA模型自回归阶数p=3，滑动平均阶数q=5，差分阶数d=1；WNN 模型学习率设为0.01，迭代次数为800次，输入层、隐藏层、输出层的个数分别为6、6、1，学习步长为6；LSTM 模型学习率设为0.01，使用的激活函数为tanh，模型层数为3层，迭代次数设为500 次；KNN-LSTM 模型中LSTM 模型参数设置同上，K的取值为3。

不同模型预测结果和性能分别如图3 和表1 所示。从图3 和表1 中可以看出，ARIMA 模型的预测性能最差，WNN 模型的性能相对深度模型较差，LSTM、KNNLSTM和KNN-BLS三种模型都比较准确地反映了真实的交通流量的变化，KNN-BLS 模型更能捕捉到交通流数据细节的波动性。相比于ARIMA、WNN、LSTM、KNN-LSTM 模型，KNN-BLS 模型预测的RMSE 分别下降98.55%、79.06%、7.857%、0.767 2%。同时可以看出，在相同的实验配置条件下，KNN-BLS 的运行时间大幅度下降，甚至优于线性模型ARIMA；虽然预测误差与深度学习模型LSTM 及KNN-LSTM 几乎相当，但是运行速率提高99%以上，表明KNN-BLS 模型可在保证预测精度的同时，大幅度减少运算时间，是一种有效的短时交通流预测方法。

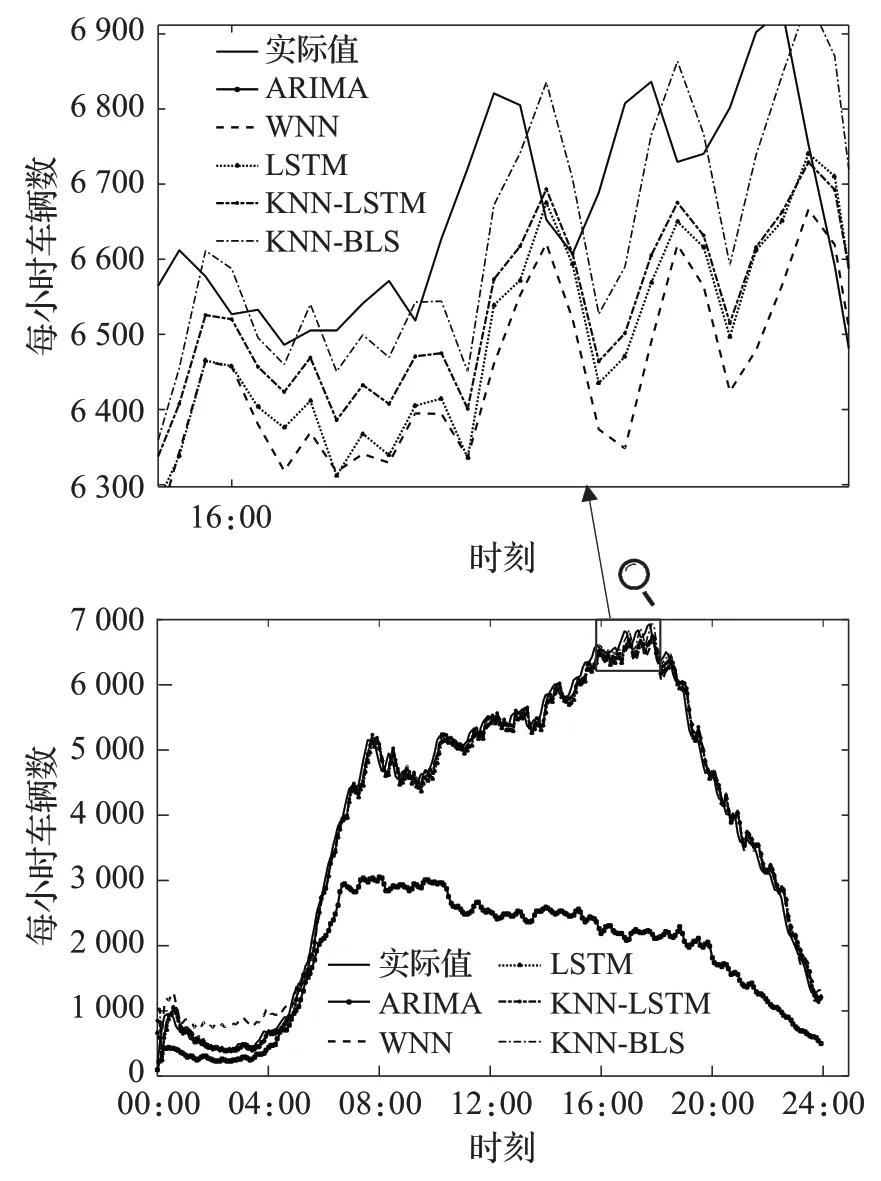
图3 不同模型预测结果Fig.3 Prediction result of different models

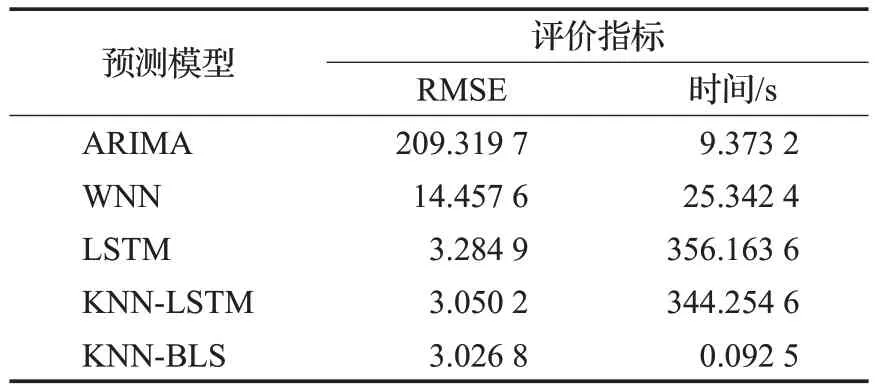
表1 不同模型预测性能Table 1 Prediction performances of different models

本文对交通流数据进行预测时，为了充分利用交通流数据的时空相关特性，通过KNN 方法选取路网中与预测路段相关的路段进行分析，相关路段的个数成为影响预测模型的重要参数。为了分析不同路段个数K对预测结果的影响，实验中取不同K值分别进行模型预测，并分别计算预测的RMSE。图4 给出了不用时空相关的路段数与预测RMSE 的关系，从图4 中可以看出，预测的RMSE 随着K的增大存在上下波动，当K=17时，对应的RMSE 达到最小值。因此，本文在实验中选择的相关路段数目为17，均位于目标路段上下游附近，其中上游12 个，下游5 个，说明预测路段的预测结果会受到相邻路段空间分布位置及数目的影响，且上游影响更大一些，与实际情况比较吻合。

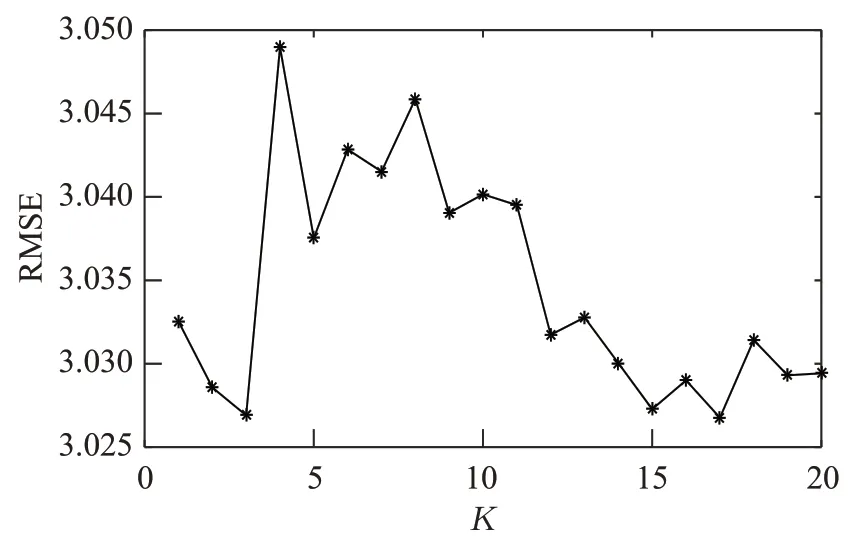
图4 不同K 值预测的RMSEFig.4 RMSE predicted by different K values

5 结束语

本文结合交通流数据的时空相关特性，提出基于KNN-BLS的短时交通流预测模型，利用PeMs数据库数据进行实验，将预测结果与ARIMA、WNN、LSTM、KNN-LSTM 模型进行对比。实验结果表明KNN-BLS模型可降低预测误差，将预测误差平均降低46.56%，是一种有效的短时交通流预测方法。同时，与深度模型相比，宽度模型在保证预测精度的前提下，缩短预测时间，将运行速率提高99%以上，是一种结构简单、预测速度快的短时交通流预测方法。

为了更好地挖掘交通流数据的时间依赖性，在未来研究工作中，考虑在宽度系统中应用一些循环系统，更深层次研究交通流数据的时序特征。同时，由于交通流数据受天气、交通事故、道路施工、节假日等诸多因素影响，在未来研究工作中，应考虑到上述因素，进一步提高预测精度。