智能博弈对抗中的对手建模方法及其应用综述

魏婷婷，袁唯淋，罗俊仁，张万鹏

国防科技大学 智能科学学院，长沙410073

近年来，人工智能技术的进步引领智能博弈对抗领域飞速发展。2017年，AlphaGo战胜人类顶级选手[1]，标志着人工智能在完全信息下的博弈对抗学习中取得了成功，围棋这一难题被彻底攻破。随后，研究人员将目光转向了不完全信息下的大规模博弈对抗，2019年，由Facebook 人工智能实验室和卡耐基梅隆大学共同研发的扑克AI 程序Pluribus 在六人无限注德州扑克比赛中击败了全球顶尖职业选手[2]。2019 年10 月，DeepMind使用多智能体强化学习（multi-agent reinforcement learning，MARL）方法训练的AlphaStar在星际争霸Ⅱ中取得大师级水平[3]，成果发表在Nature杂志上，智能博弈对抗研究进展如图1 所示。智能博弈对抗技术在国土安全和军事指挥与控制领域都扮演着重要的角色。从民事应用来看，智能博弈对抗技术的应用范围广泛，涵盖了军事规划与指挥、反恐与国土安全、信息安全、即时策略游戏（real-time strategy，RTS）等实际问题。在军事指挥与控制领域攻防对抗中，随着博弈对抗规模的扩大，对抗空间呈现指数级增长，多方协同与环境耦合的问题凸显，战争系统具有强非线性和高动态等复杂特性，解析计算和随机逼近最佳策略都存在巨大挑战，智能博弈对抗的策略学习需要着力研究对手行为建模和协同演化策略学习方法，以不断提升对抗能力。

图1 智能博弈对抗研究进展Fig.1 Progress of intelligent game confrontation research

对手建模研究在过去二十年取得了重大进展，是指在对抗环境下，考虑如何对除自己以外其他智能体进行行为建模，是一种典型的行为预测技术[4]。智能博弈对抗策略学习的许多相关研究都关注于开发能够与其他智能体有效交互的自主智能体，对手建模作为其中最重要的方法之一，通过构建模型来分析或预测交互环境中其他智能体的各种值得关注的属性（如行动、目标、策略类型），进而推理它们的行为。目前不同研究领域存在着各种建模方法，它们的基本假设均不相同，以满足其各自实际应用中的需要。在攻防对抗场景中，由于环境是部分可观测的，博弈中存在诸多的不确定性，通过对对手进行建模，识别其意图并加以利用，可以更有效地辅助决策。在多智能体系统（multi-agent system，MAS）中，通过对智能体建模，可以推测智能体动作、目标、策略等相关属性，为辅助决策提供关键信息。在军事应用中，指挥控制命令的生成必须以敌我双方的作战态势为依据，因此建立一个准确的敌方行为预测模型对于分析其意图尤其重要，基于此，己方才能最大限度地达到军事目的，以限制或操纵敌方。

对手建模的研究已经逐步从理论落地到实际应用。2004年，DARPA启动的实时对抗智能决策项目（real-time adversarial intelligence and decision-making，RAID），旨在根据当前可用的信息估算未来战争态势。2017 年，DARPA提出了马赛克作战概念[5]，期望运用智能技术来提升决策的快速性和有效性，通过对手建模，分析敌方策略，采用相应措施干扰敌方并增加敌方决策复杂度。2019 年，美国国防高级研究计划局（DARPA）的空战演进计划（air combat evolution，ACE）开始着手将AI飞行员由虚拟仿真推向实机对抗[6]。对手建模在竞技类游戏和军事仿真推演等领域的应用前景广阔，因此研究对手模型建立与利用具有重要意义。

1 对手建模内涵

对手建模研究由来已久，最早在博弈论框架下进行相关研究，是博弈论范式下的子课题，许多对手建模的方法受到博弈理论的启发而提出。博弈论是在现实世界竞争中人类行为模式的基石，研究理性参与者决策的相互作用及其均衡问题，使得个体通过竞争与合作实现自身利益最大化。在博弈论中，纳什均衡[7]是博弈的最优解，可利用性衡量的是一个策略与纳什均衡策略之间的距离，其大小表征了纳什策略可利用性的强弱。对手建模以可观测的历史数据作为输入，最终得到关于智能体某些属性的预测，如图2所示。

图2 对手建模过程Fig.2 Process of opponent modeling

建立对手模型的目的是智能体能够适应对手并利用其弱点来提高智能体的决策能力，即使已知均衡解，利用准确的对手模型仍有可能获得更高的奖励。为了易于处理问题，对手建模研究通常假设对手遵循固定的策略，与平稳假设相反的策略称为非平稳策略。Albrecht等人从总体上归纳了对手建模方法[8]，主要分为以下几类：策略重构[9-10]，即建立模型对对手的行动做出明确的预测来重建对手的决策过程；基于类型的推理[11]，假设对手有几种已知类型中的一种，并使用在实时交互过程中获得的新观察来更新信念；分类方法[12]，模型将类别标签（例如，“攻击性”或“防御性”）分配给对手，并采用对该特定类别的对手有效的预计算策略；规划行动意图识别[13]，使用层次化规划库或域理论，预测智能体的目标和可能行为；递归推理[14-15]，对嵌套信念进行建模（例如，“我相信你相信我相信……”）并模拟对手的推理过程来预测他们的行动，递归持续推理其他智能体的可能模型并预测其可能行为，但是往往递归层次难以分析，理性假设太强。

由于非平稳环境下的博弈对抗愈演愈烈，平稳假设会严重限制系统的适用性和准确性，迫切地需要对动态的对手策略进行建模，以此为基础进行反制策略的研究。本文旨在从非平稳角度出发，对现有的对手建模方法及其应用进行总结归纳。

1.1 面临的挑战

通常情况下，博弈对抗中的智能体被认为是完全理性的，但在扑克、星际争霸等不完美信息动态博弈对抗中，智能体所处的环境是部分可观测的，人类参与者往往具有有限理性，无法做出最佳的策略。决策任务中对手策略的不固定性带来的非平稳问题一直是博弈论、强化学习等领域研究的热点，现有的方法大多数是通过学习其他智能体的模型来预测它们的行为，从而消除非平稳行为。

根据智能体所处环境特性的不同，进行对手建模时所考虑的条件以及建模的方式往往也不同。现有的一些研究工作往往将其他智能体看作是环境的一部分，不考虑由智能体主体参与引起的非平稳，忽略其他智能体的影响，优化策略的同时假设了一个平稳的环境，将非平稳问题视为随机波动进行处理。当对手策略固定的情况下，将对手也视为平稳环境的一部分是一种有效简化方法，然而，在对手策略是学习型缓慢变化或动态切换变化时，需要充分考虑环境的非平稳性。在多智能体场景下，将智能体视为非平稳环境的一部分并不合理，因此，考虑环境的非平稳性，针对能够自主学习的对手，有必要进行对手建模，以预测对手的行为和评估对手的能力。

从环境可观测性和对手行为变化程度两个维度对对手建模方法进行分析，目前应对“对手”的主要方法分为五类[16]：忽略（ignore）、遗忘（forget）、目标对手最佳反应（respond to target models）、学习对手模型（learn models）和心智理论（theory of mind，ToM）。博弈对抗环境根据可观测性按递增顺序分为四类：局部奖励、对手动作、对手动作与奖励、完整先验知识。环境的部分可观察性对于智能体学习带来了很大的不确定性，如存在欺骗利用的环境中，有些奖励可能是虚假的。此外，在对抗交互中，对手也在不断地适应和学习，因此对手改变其行为的能力也是一个重要的考虑方面，按其行为变化剧烈程度由低到高分为：固定策略（no adaptation）、缓慢改变（slow adaptation）、剧烈变化（drastic or abrupt adaptation）。不同的方法均对对手做了类似的假设，有些方法假设对手策略固定，那么在非平稳环境无法适用。由环境可观测性、对手行为变化程度和智能体应对变化的能力组成的博弈对抗空间复杂性如图3所示。

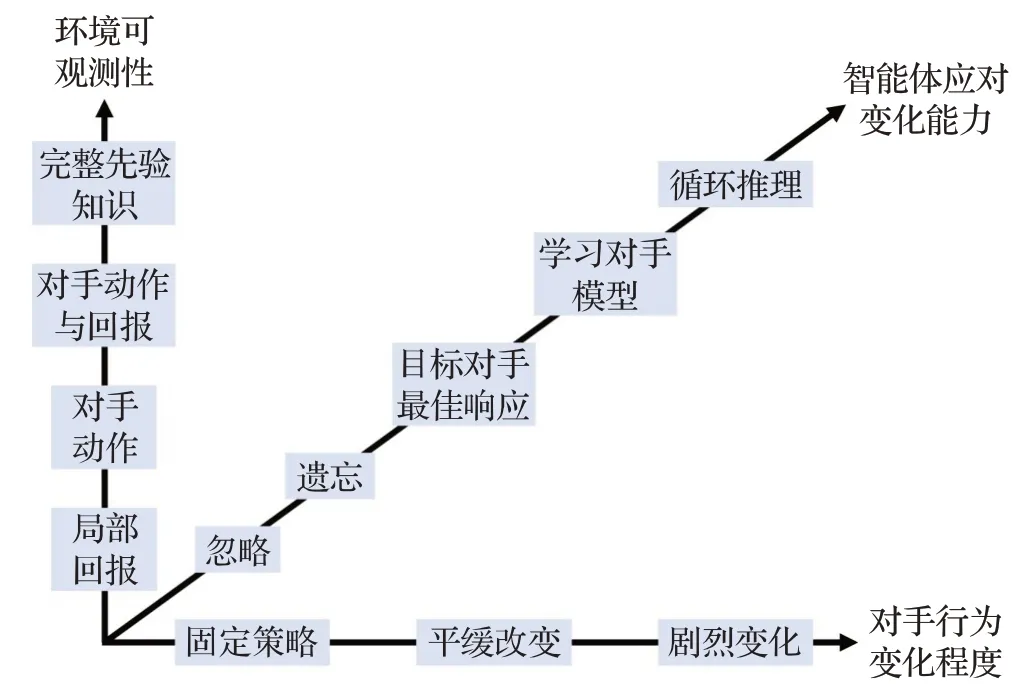
图3 博弈对抗空间复杂性Fig.3 Complexity of game confrontation space

1.2 建模方式分类

目前的大部分研究将对手建模方法分为隐式建模和显式建模[17]，具体建模过程及区别如图4所示。

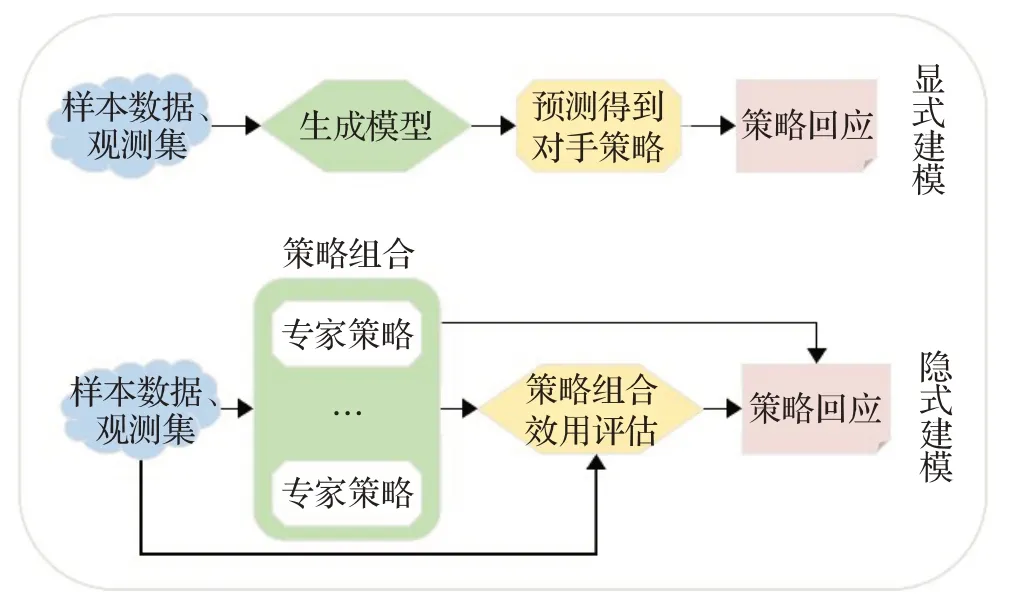
图4 显式对手建模与隐式对手建模Fig.4 Explicit and implicit opponent modeling

显式建模通常直接根据观测到的对手历史行为数据进行推理优化，通过模型拟合对手行为策略，掌握对手意图，降低对手信息缺失带来的影响，并且对其他方法的适配兼容效果更好。隐式建模则直接将对手信息作为自身博弈模型的一部分处理对手信息缺失的问题，通过最大化智能体期望回报的方式将对手的决策行为隐式引进自身模型，构成隐式建模方法。显式模型提供了一种直接的方式来表示智能体的行为，但在没有一定的先验知识的情况下，建立精确的模型需要大量的样本。对于不完美信息领域，由于对手信息的缺乏，使得显式建模难以实现。隐式建模则是编码智能体某些方面的行为特征，而不做出明确的预测。

2 对手建模方法

随着深度神经网络的兴起，对手建模研究结合诸多领域，涌现出很多前沿的多智能体对手建模方法。本文基于现有的研究，将一些前沿的对手建模方法做如下分类：（1）基于策略表征的学习方法。由于深度学习技术的成熟使得网络表征能力变强，许多研究使用深度强化学习预测对手行为策略，通过正则化的方法提高泛化能力，使用元学习的手段在少量交互的条件下快速适应对手。（2）基于认知建模的推理方法。心智理论是现实生活中人类进行交互的认知理论科学，在人对抗交互中，对抗双方都会对对方行为模型产生认知，研究者开发了机器心智理论；在有限理性研究中，基于层次理论赋予智能体K级推理能力；在对手具有信念的前提下，通过递归推理的方法应对对手。（3）基于贝叶斯的优化方法。贝叶斯推理为对手建模与利用提供了理论基础，已知对手策略先验分布和对弈观察的情况下，贝叶斯推理可以得到对手策略空间的后验分布，进而推断后验策略并加以利用。对手建模方法层次与典型的前沿对手建模方法分别如图5和表1[18-34]所示，以下分别进行详细介绍。

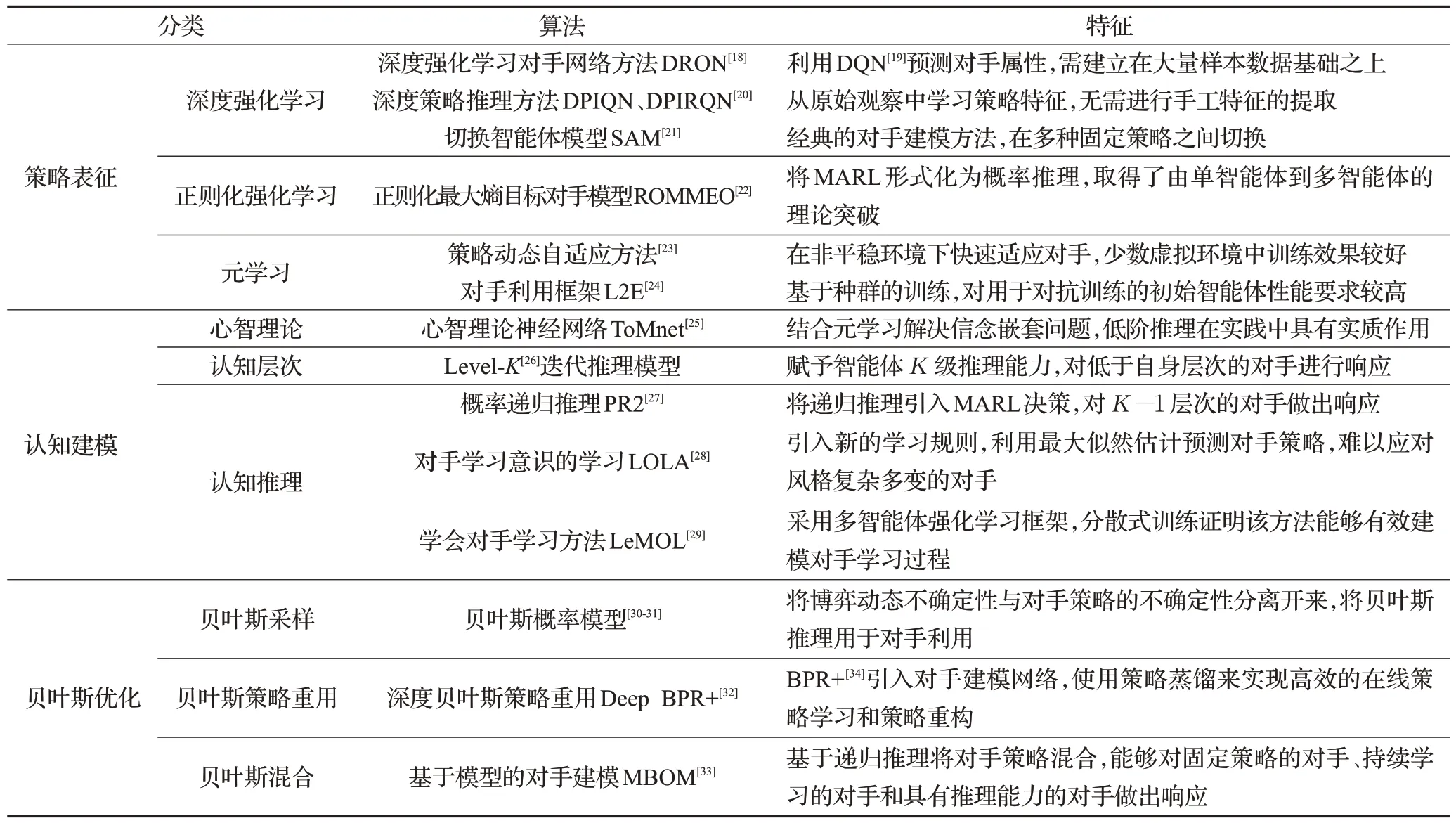
表1 典型前沿对手建模方法Table 1 Typical cutting-edge opponent modeling methods

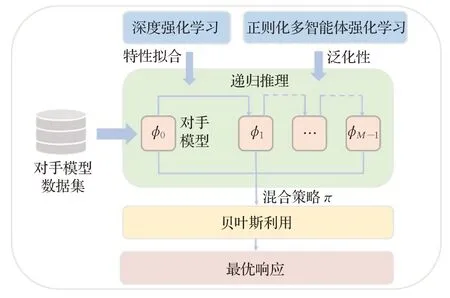
图5 对手建模方法层次Fig.5 Hierarchy of opponent modeling methods

2.1 基于策略表征的学习方法

2.1.1 基于深度强化学习的方法

对手建模的两个关键问题是选择对手特征参数进行建模以及如何使用这些预测信息，深度学习由于具有强大表征能力，结合博弈论、认知心理学，涌现出许多优异的对手建模方法，并且解决了研究领域诸多问题。基于深度学习的方法[35]解决了依赖专家知识人工提取特征的问题，通过拟合能够学习到高度灵活的模型，可以达到自动执行认知建模的目的，以此来预测人类的行为。一种深度强化学习对手网络方法（deep reinforcement opponent network，DRON）[18]在DQN（deep Q-network）[19]的基础上提出，包含一个预测Q值的策略学习模块和一个推断对手策略的对手学习模块，根据过去的观察隐式地预测对手的属性，在此基础上还使用了混合专家网络改进Q 值估计的方法。DRON 将神经网络应用于对手建模，结合强化学习以解决更复杂的决策问题，其能够处理不完全信息博弈问题，但需要建立在大量的历史数据基础之上。深度策略推理方法（deep policy inference Q-network，DPIQN）和引入LSTM[36]循环神经网络的深度循环策略推理方法（deep recurrent policy inference Q-network，DPIRQN）[20]通过制定辅助手段来额外学习这些策略特征，直接从其他智能体的原始观察中进行学习，无需像DRON一样采用手工特征（handcrafted features），即人工选取的特征。

2.1.2 基于正则化强化学习的方法

神经网络的拟合能力非常强，但是也容易造成过拟合，在测试集上的错误率会很高。正则化（regularization）是一类通过限制模型复杂度，从而避免过拟合，提高泛化能力的方法，包括引入一些约束规则、增加先验、提前停止等。一种正则化最大熵目标对手模型（regularized opponent model with maximum entropy objective，ROMMEO）[22]将MARL形式化为概率推理问题，通过引入相关项（记为ρ）可以防止建立的对手模型偏离实际，用对手模型和先验之间的KL（Kullback-Leibler）散度作为ρ的正则化器，通过设定对手过往行为的先验经验分布，对偏离经验分布的情况，KL散度将对ρ做出严重惩罚（由于方程中的目标可以看作是一个智能体的策略和对对手模型进行正则化的最大熵目标，此目标称为正则化最大熵目标对手模型），虽然ROMMEO 实现了理论上的推导，但其验证场景为完美信息博弈，对于实际的不完美信息博弈问题的求解效果未知。

2.1.3 基于元学习的方法

元学习（meta-learning或learning-to-learn）[37]是机器学习领域的新趋势，它利用训练阶段的经验来学习如何学习，获得对新环境或新任务进行概括的能力，元学习在对手建模中的应用也有一些初步的研究成果。来自卡耐基梅隆大学和OpenAI的研究团队提出策略动态自适应的方法[23]使用元学习算法MAML[38]来处理多智能体交互中的非平稳问题，研究如何在非平稳环境中，快速学习到相应的策略，该方法将非平稳环境视为一系列静态任务，训练智能体利用连续任务之间的依赖关系，但仅在少数对抗环境中取得了比基准算法性能好的效果。虽然多数结合元学习的方法训练效果一般，但作为一种新的对手建模求解思路，其建模方法本质是学会对手学习，进而求解最佳响应。对手建模问题本质上是跟谁打（who to battle）和怎么打（how to battle）的问题，对手利用框架（learning to exploit，L2E）[24]通过元学习的方法进行隐式对手建模，提出了一个多样性正则化的策略生成算法，可以自动产生难被利用的（hard-to-exploit）和多样化（diverse）的对手，提高了算法的鲁棒性和泛化能力，但其对最初生成的智能体性能要求较高。

2.2 基于认知建模的推理方法

2.2.1 基于心智理论的方法

博弈论无法解释有限理性人的博弈决策行为，研究者借鉴人类心智理论，进行了机器心智理论的相关探索。心智理论是脑神经科学与认知科学领域中面向信息交互的认知行为理论，是认知推理智能的主要表现形式。认知科学领域的许多研究表明，人类经常利用这种能力来理解和预测他人的行为，甚至通过递归地推理他人如何使用这种能力理解自己的行为，进而演化出更高阶的心智理论。相关研究工作已经表明，借鉴人类心智理论模型开发多智能体系统不仅可以提升AI的推理和决策能力层级，还有望改进当前人工智能领域存在不可解释性的重要缺陷。DeepMind的研究人员提出了心智理论神经网络（theory of mind neural network，ToMnet）[25]方法，使用元学习的方法构建了一个强大的先验模型，来提高对对手未来行为的预测，智能体具备思考和判断的能力，能产生对手信念并对其进行判断，提高了AI的可解释性。在一些游戏中，研究人员证明了一阶和二阶心智理论具有实质性的作用，而高阶心智理论却具有较低的投资回报率[39-40]。

2.2.2 基于认知层次的方法

智能体能产生对手信念，反之对手也能产生对智能体的信念，从而出现了信念嵌套。认知层次（cognitive hierarchy，CH）[41]模型无需求解博弈中的纳什均衡，增强了可解释性的同时，实现了对手建模算法从“感知”到“认知”的过渡。认知层次模型指出参与者具有思考步数，K步思考能力即认知层次为K，其大小代表了认知层次的高低，K级智能体可以推理得到低于K级的对手的推理逻辑和策略分布，并且可以对所有低于K级认知层次的对手做出最优反应。虽然理论上CH可以对低于自身层次的任何对手做出响应，但如何针对对手策略进行更加准确地预测以及迭代步数的选择仍需继续探索。Level-K迭代推理模型[26]赋予了智能体K级推理能力，对对手的行为预测的基础上进行K轮的迭代推理，与认知层次的区别在于K级的智能体对K-1 级做出最佳响应，针对对手层次的假设也直接限制了智能体对其他层次对手的响应能力。

2.2.3 基于递归推理的方法

递归推理表示了一种认知层次的高低，将递归推理应用于对手建模研究有助于建立具备推理对手行为、目标和信念的智能体。UCL的研究团队提出了MARL的概率递归推理（probabilistic recursive reasoning，PR2）[27]框架，首次将递归推理引入MARL 决策中，是对手建模的一个新的思路。传统的对手建模方法可以被看作是0级递归推理，由于对对手更高级别的策略响应都要建立在0 级对手的基础之上，因此0 级对手的选取是进行迭代推理、预测智能体行为的基础模型，该模型直接影响更高层次的智能体的性能。Level-0 迭代模型[42]利用博弈领域的知识进行特征的选取，为0级对手提供了一种可靠的描述方式，针对具体的模型，需要调整相关特征权重以避免过拟合，防止预测性能降低。

对手意识（opponent awareness）在一些研究中被用来表征对对手的认知建模，本质上是采用相关理论对策略梯度进行推导求解。对手学习意识的学习（learning with opponent-learning awareness，LOLA）[28]则通过引入新的学习规则对对手策略参数更新进行预测，并对预测的行为做出最佳相应，通过对对手状态-动作轨迹的观察采用最大似然估计以求得对手策略参数的估计值，对手建模技术的引入解决了对抗环境下对手策略参数未知的问题，但对于风格复杂多变的对手，往往应对困难。伦敦大学学院（University College London，UCL）的研究团队使用RL2[43]提出学会对手学习方法（LeMOL）[29]采取多智能体强化学习的框架，使用对手模型弥补了分散式训练中无法访问其他智能体策略的缺点，同基线算法集中式MADDPG[44]相比，性能有一定提升。

2.3 基于贝叶斯的优化方法

由于现实博弈中纳什均衡的难计算、对手风格多变以及对手弱点可利用的特点，需要为其建立鲁棒性高的方法，贝叶斯推理为对手建模与利用提供了很好的理论基础。在给定先验分布和对弈观察的情况下，根据贝叶斯推理可以得到对手策略空间的后验分布推断对手的后验策略，用β表示对手的行为策略，给定一个O=Os∪Of的观察集，其中Os是导致摊牌的回合的观察集，Of是导致折叠弃牌的回合的观察集，Hs和Hf分别表示摊牌和弃牌的情况，根据贝叶斯规则可以得到：

贝叶斯方法的建模效果与先验知识有关，对于更难对付的对手，如果有更加完备的先验知识，对抗效果将更好。在得到对手行为策略分布之后，如何进行决策响应也是一个关键的环节，一种基于贝叶斯概率的模型[30]，将博弈动态不确定性与对手策略的不确定性分离开来，使用贝叶斯最佳响应（Bayesian best response，BBR）、最大后验响应（max a posteriori response，MAP）和汤普森响应（Thompson’s response）3种应对策略，其平均收益和平均胜率均不低于纳什策略和当时先进的对手建模技术，并且能够在短时间内快速适应对手并加以利用。深度贝叶斯策略重用（deep Bayesian policy reuse，deep BPR+）[32]在BPR+[34]上面增加了一个对手建模网络，同时结合策略蒸馏[45]的方法，算法包含策略重用和新策略学习两个阶段，提高了学习新策略的效率和对对手策略判断的准确性。基于模型的对手建模MBOM[33]将想象的对手策略与真实的对手进行相似性比较，将多种策略进行混合，以求得对手的最佳响应，该方法结合递归推理与贝叶斯推理来预测对手的学习，在竞争和合作环境中，MBOM对于固定策略、持续学习和具有推理能力的对手都有很好的适应能力。

3 对手建模方法典型应用分析

对手模型的建立对于处理复杂情况下的博弈对抗来说是非常必要的（如电子游戏、扑克等），是利用次优对手的关键。本章介绍序贯博弈对抗（德州扑克）、即时策略博弈对抗（星际争霸）和元博弈中对手建模方法的具体应用。

3.1 序贯策略博弈

在德州扑克的机器博弈中，对手建模可以有效评估对手策略、找出对手弱点，利用对手的弱点往往能取得比纳什均衡策略更高的收益。与围棋不同，扑克由于对手手牌信息的私有性导致牌局信息不完美可知，求解空间复杂，难以搜寻均衡解，随着冷扑大师Libratus[46]和Pluribus先后在双人无限扑克和多人无限扑克中战胜人类顶级玩家，德州扑克已然被当作大规模不完美信息动态博弈的重要测试环境。对手建模是德州扑克智能博弈中一个重要的研究方向，与斗地主、麻将等计算机扑克相比，参与者的目的不止是赢，更是希望在比赛结束时从对手那里赢得尽可能多的筹码，德州扑克中参与者采用的策略以及暴露出的弱点可以加以利用，因此建立一个清晰的模型来预测对手的行为尤为重要。

在德州扑克中进行对手建模，一般包括手牌范围建模和行为习惯建模两部分，首先要进行对手策略类型及风格类型分析与手牌评估，然后基于已有的样本数据拟合最优解。传统的方法主要有策略偏向、决策树、贝叶斯推理、神经网络、多智能体投票建模等方法[47-50]。对手建模结合深度学习技术，与多领域知识融合，形成了以神经演化算法[51]为代表的前沿技术。传统的基于规则的方法大多依赖于专家知识，结合深度学习的前沿对手建模技术可以在不具备相关领域知识的情况下取得不错的效果，拟合性能良好，但大多属于隐式建模方法，模型可解释性不足。

3.1.1 特定对手最佳响应

在实际的博弈当中，博弈过程中的博弈者的类型是多种多样的，将博弈者的策略进行抽象归纳是一种常用的方法[52]。在德州扑克游戏中，博弈过程中的博弈者类型可以分为以下5种，分别为进攻型、常规型、防守型、吓唬型以及狡诈型[53]，每种类型都有其优势与劣势。在实际的博弈当中，在同一博弈状态下，针对不同类型的博弈者可以做出不同策略，要做到这一点，对于对手模型的建立就很有必要了，德州扑克中的对手建模框架如图6所示。

对手当前策略的信念可以被编码成一种策略，先验或者后验信念可以总结为一个函数，该函数即为信息集到行动的映射，即预期的对手策略。对手模型本身可以作为一种策略，也包含了对抗被对手利用的反制策略，这种反制策略的有效性在关于限制纳什反应的研究中得到了证明。然而在一些情况下，对手模型只是基于少量观察样本而构建的，所以重点是研究如何与实际情况中的对手进行对抗。限制性纳什响应反制策略（restricted Nash response，RNR）[54]是德州扑克中一种典型的对手建模的方法，可以在特定对手模型最佳策略和纳什均衡之间找到具有鲁棒性的反制策略，最大化利用对手的同时最小化损失。RNR通过选择一个参数来表示整个对手模型的准确度，并且存在过拟合、需要大量观测以及对训练对手的选择较为敏感的缺陷。数据偏差响应（data biased responses，DBR）[55]方法通过对每个信息集赋予一个置信度，从而建立一个更为可靠的鲁棒反制策略对手模型。

3.1.2 神经演化学习

基于纳什均衡的方法[56]在多智能体博弈领域取得了成功，但它们缺乏有效的建模和利用对手的能力。基于循环神经网络LSTM 和模式识别树（PRTs）的对手模型[51]，通过进化优化构建基于模式识别树和LSTM神经网络的对手模型，然后将此类模型与决策方法集成，以建立能够利用对手弱点以调整其行为的扑克智能体。通过这种方法，构建了一个德州扑克自适应系统（adaptive system of Hold’em，ASHE），包括RPT、LSTM 估计器和决策方法，方法的核心是对手模型，它包含PRT 和两个LSTM估计器。RPT本质上是一个特征提取器，收集对手在每一场游戏中的策略信息，从不同的博弈状态中提取有用的统计特征，作为输入传给LSTM 估计器。LSTM估计器的精度决定了方法的性能，其将估计的摊牌胜率和对手弃牌率输入到决策方法，该方法基于统计估计每个可能动作的期望收益，并相应地选择最佳动作。该扑克智能体可以适应在训练中从未见过的对手，并且能够有效地利用对手的弱点，这种方法可以拓展到其他不完美信息博弈问题建模和利用弱的对手。

3.1.3 策略集成学习

集成学习（ensemble learning）[57]是指将多个分类器（可以为同质，也可以为异质）组合成一个比单个分类器更强大的系统，即便某一个分类器得到了错误的预测，其他的分类器也可以将错误纠正回来，因此集成学习系统可以博采众长，具有比单个分类器更高的预测性能以及更好的泛化能力。在德州扑克中，集成学习方法[58]在对手策略建模中的作用为将特征映射到决策，即用于发现它们之间的复杂关系。集成学习系统首先训练了几个专家，每个专家针对一个特定的参与者进行训练。通过随机选择所有参与者的专家并进行交叉验证，对未知对手行为预测的准确率比单个分类器的结果更高。因此，集成学习可以为基于已有异构分类模型快速构造通用的对手模型提供支撑，提高对未知对手的预测性能，提高模型泛化能力，对手建模集成学习框架如图7所示。

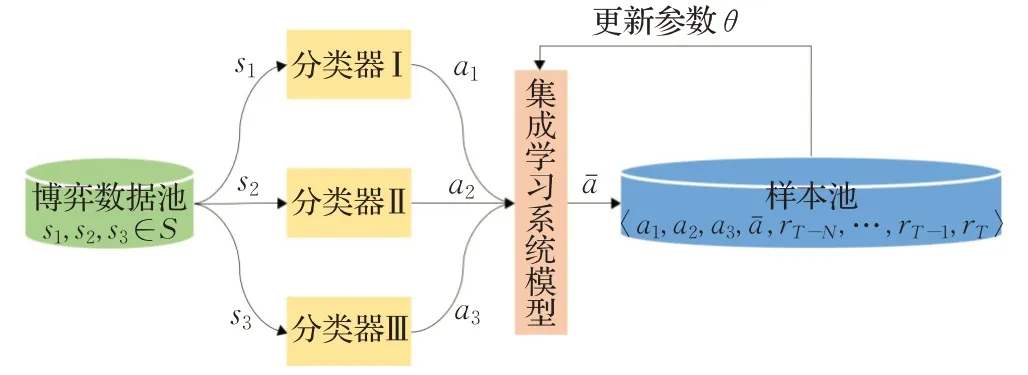
图7 对手建模集成学习框架Fig.7 Framework of opponent modeling for ensemble learning

不完美信息不确定性条件下，基于不同范式构建的初级决策模型具有不同偏好，在模型精确性、安全性、鲁棒性方面的各有优缺点。多范式多目标可解释性策略集成方法的研究建立在构建初级决策模型的基础上，需要考虑如何在尽可能保留可解释性决策依据的同时，一方面提高决策收益，另一方面降低决策模型的对手可利用度。

3.2 即时策略博弈

在星际争霸为代表的多智能体博弈对抗中，对手建模为智能体的开发提供了新的思路。即时策略博弈相较于棋类游戏更为复杂，状态空间更大，决策时间要求更快，除了不完美信息带来了很大的不确定性外，还要考虑动作的连续性、多异构智能体合作[59]等诸多问题。星际争霸中涉及对手建模的算法主要包括经典机器学习方法和虚拟对弈方法。经典的机器学习方法通常需要大量的历史交互数据进行特征拟合，但高质量的样本数据往往稀缺，难以支撑复杂深层网络的收敛需求；虚拟对弈是求解大规模不完美信息博弈的有效算法，在策略优化过程中无需先验知识，通过构建对手策略池进行虚拟对弈，提升策略质量。以下分别进行介绍上述两种对手建模方法。

3.2.1 经典机器学习方法

经典的机器学习方法对手建模的思路通常为用数据拟合行为策略特征，由于星际争霸I 保存了回放的功能，可以下载游戏日志，传统的方法一般通过保存的游戏数据进行研究。一种基于数据挖掘的策略博弈对手建模方法[60]使用机器学习识别对手的策略，以及预测对手行为，通过将游戏日志编码为特征向量，将对手策略预测转换为了分类问题。一种类似的方法[61]也是从回放数据中学习不能直接建模作战模型参数，估计的模型优于手工提取的模型。用于星际争霸的一种聚类方法[62]使用K-Means 算法将参与者的策略从有限的策略集中进行分类。对抗层次任务网络（adversarial hierarchical task network，AHTN）[63]规划将极小极大值搜索算法与分层任务分解（hierarchical task decomposition，HTN）相结合，已成功应用于RTS游戏，但是并没有考虑对手的因素，AHTNCO方法[64]在此基础之上引入对手建模，通过对手策略来模拟对手行为，采用对手策略生成最小节点，直到找到第一个可行的动作，再执行该动作并生成最大节点。

3.2.2 虚拟对弈方法

虚拟对弈（fictitious play，FP）[65]近年来被用来解决星际争霸、DOTA2 等大规模不完美信息博弈问题。FP是一种传统的基于对弈的不完美博弈均衡求解方法，每个参与者在对弈中保持两个策略：平均策略（average strategies）和最优反应策略（best response），每个参与者在对弈中不断地采取对手平均策略的最优反应策略，则其平均策略在两人零和博弈中收敛至纳什均衡。根据从对手策略池中不同“挑选对手”和“应对对手”的方法，虚拟对弈衍生出神经虚拟自对弈、种群训练（populationbased training，PBT）等变体，如图8所示。

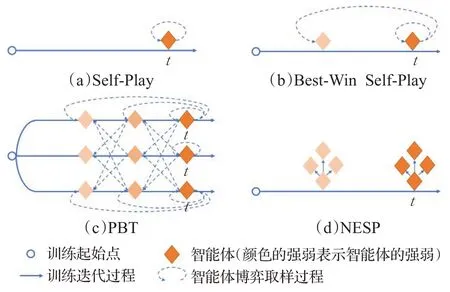
图8 虚拟对弈衍生变体示意图Fig.8 Variants of fictitious play

虚拟自对弈（fictitious self-play，FSP）[66]将博弈论和机器学习的方法相结合，分别通过基于强化学习方法和基于样本的监督学习逼近最佳响应和平均策略。神经虚拟自对弈方法（neural fictitious self-play，NFSP）[67]将FSP与神经网络近似函数相结合，是一个在不完美信息中不需要先验知识就能学习到近似纳什均衡的端到端的强化学习技术。NFSP中的最佳反应依赖于深度Q学习的计算，收敛时间长。来自浙大的研究团队提出了异步神经虚拟自对弈（asynchronous neural fictitious self play，ANFSP）[68]方法，以更快更稳地接近近似纳什均衡，该方法在德州扑克和第一人称射击游戏（FPS）中均取得了不错表现。FSP 的变体优先虚拟自对弈的方法（prioritized fictitious self-play，PFSP）[3]已经成功应用于AlphaStar，DeepMind 创新性地提出联赛训练（league training）的概念，即保留所有训练中产生的历史版本，并将每一代训练的AI 都放到训练池中进行互相对抗，全方位提升了AI 的水平，这种基于种群的训练方法是对手建模的一种方式。

3.3 元博弈方法

策略空间响应Oracles（policy-space response oracles，PSRO）[69]作为博弈论与强化学习算法结合的产物，通过模拟所有参与者策略配对的结果，构建了一个更通用的博弈，即元博弈（meta-game），其根据已有的元博弈策略的分布为每个参与者训练新策略，然后将这些新策略添加策略池中，并进行迭代，如图9所示。

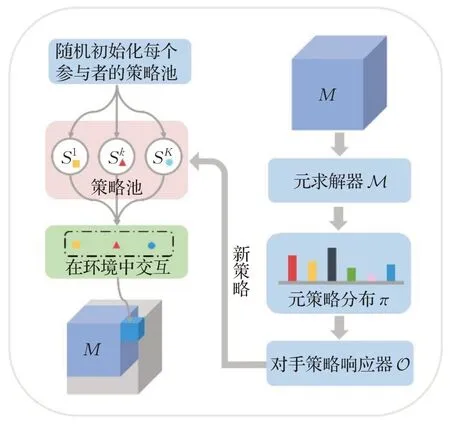
图9 元博弈策略学习框架Fig.9 Framework of meta-game strategy learning

PSRO 使用混合元策略，可以防止对特定策略的响应过度拟合，并且能够产生安全利用对手的鲁棒反策略。由于一般性博弈（如多人博弈）中纳什均衡难以计算，DeepMind 研究人员提了出纳什均衡的替代解α-Rank[70]作为元求解器，将PSRO 扩展到了多人博弈[71]。PSRO极具概括性，可以将FSP的思想融入MARL，成为了一种通用的算法框架。一种管道PSRO（pipeline PSRO，P2SRO）[72]方法通过并行化来解决大规模不完美信息博弈策略学习收敛速度慢的问题。

4 研究展望

4.1 有限理性对手建模

通常情况下博弈参与者被认为是绝对理性的，然而在现实的场景中人类参与者往往无法做出最佳策略，即对手行为偏离博弈中的均衡解。MARL 模型中一般假设的是完全理性的智能体，实际上个体的认知是有限制的，进行决策时也会受个人偏好等诸多方面的影响。在重复博弈过程中，高水平的参与者逐渐适应对手的打法后，试图“操控”博弈过程时也会表现出非理性行为。例如：通过设计巧妙的“陷阱”，暂时放弃短期的最优收益，诱使对手做出错误的决策，以获得长期的收益。开展对有限理性参与者的建模，有助于机器心智理论的研究，提高机器智能可解释性。

4.2 策略欺骗性对手建模

欺骗与反欺骗是一种广泛存在的对抗形式，在人工智能领域更是屡见不鲜，如：图灵测试、电磁对抗、Deepfake技术等，但在博弈对抗中欺骗的研究方兴未艾。纳什策略往往过于保守，实现低可利用性的同时却降低了对对手弱点的利用，因此寻求安全性和对手利用之间的平衡点仍然是值得研究的问题[73-74]。以扑克游戏为例，参与者可以通过采用诈唬的手段混淆对手的认知，欺骗对手从而达到赢得对局的目的。欺骗方法研究是博弈学习中的难点，如何有效地利用欺骗手段并识别对手的欺骗，有待继续深入研究[75]。

4.3 可解释性对手建模

可解释人工智能（explainable artificial intelligence，XAI）是一个新兴的多学科研究领域。2016 年，DARPA提出“可解释人工智能”项目，计划构建一类方法，使之“能够解释它们的基本原理，描述它们的优缺点，并传达关于它们未来行为的解读”。从模型安全角度考虑，对手模型的可解释性极其关键，为最优决策提供安全性支撑。当前关于对手建模与利用的人工智能方法，在推理结果的可解释性上表现不足。研究如何使智能系统的行为对人类更透明、更易懂、更可信将是未来的热点方向之一。

5 结束语

己方策略的制定必须以博弈对抗各方的行动策略为前提，建立一个准确的对手行为模型以预测对手意图尤其重要。对手建模作为多智能体博弈对抗的理论基础和技术支撑之一，与博弈论和强化学习方法相互结合，以解决复杂环境下的智能博弈决策问题在推测敌对智能体动作、目标、策略等相关属性的同时，降低智能体策略的可利用性，最大程度安全利用对手，为博弈策略制定提供支撑。本文着眼于智能博弈对抗需求，以对手建模理论为核心，阐述对手建模必要性，总结分类现有对手建模方式，分析智能博弈对抗中的对手建模前沿关键技术、典型应用以及存在的主要挑战。对手建模结合博弈理论和强化学习的研究虽然已经成果丰硕，但如何向具有“有限理性、欺骗性、可解释性”等特点的复杂应用场景中迁移，仍是未来值得深入研究的问题。