鲁棒双参数化间隔支持向量机

马婷婷，杨志霞，叶俊佑

新疆大学 数学与系统科学学院，乌鲁木齐830046

支持向量机（support vector machine，SVM）是一种有监督的学习算法，通常用于分类或回归问题[1-5]。众所周知，起初支持向量机是由Vapnik 提出[4-5]，基于结构风险最小化原理和最大间隔思想构造的优化模型，具有良好的泛化性能，在文本分类[6]、模式识别[7]、金融回归[8]、计算生物学[9]等领域都有广泛的应用。当前，研究者们发展了许多支持向量机的扩展版本，如文献[10-11]。特别地，受广义特征值中心支持向量机（generalized eigenvalue proximal support vector machine，GEPSVM）[12]的启发，Jayadeva 等人提出了一种基于非平行边界超平面思想的双支持向量机（twin support vector machine，TWSVM）[13]。双支持向量机是通过求解一对较小规模的二次规划问题来寻找两个非平行超平面，从而使双支持向量机的学习效率大约比标准支持向量机快4倍。最近，双支持向量机也出现了许多变形版本，如文献[14-17]。尤其，文献[14]提出的双参数化间隔支持向量机（twinparametric-margin support vector machine，TPMSVM）。利用了参数化间隔思想，使得该方法具有一定的抗噪声能力。

上述所提及的方法，均是在训练集中的样本点是精确的假设前提下而提出的。然而，在实际应用中，训练集中的样本点，通常会受到测量误差和统计误差的干扰，导致无法得到完全精确的数据。Goldfarb等人在文献[18]中指出，输入空间中的误差会在决策时被放大导致错误决策。因此，探索能够对这种扰动数据具有鲁棒性的学习算法是很有意义的。

近年来，针对扰动数据提出了不同类型的鲁棒支持向量机。文献[18-22]主要采用二阶锥规划（SOCP）构建了鲁棒模型。Xu 等人[23-24]提出了一类非盒型不确定性集的鲁棒分类方法。Bi等人[25]考虑了一个统计框架，其中不确定数据被假设为一个隐藏的混合成分。此外，Tzelepis等人[26]认为训练集是服从已知的均值和协方差矩阵的多元高斯分布，其中每个样本对应一个不同的协方差矩阵来表示数据的不确定性。其他相关研究也可在文献[27-29]中找到。

在本文中，受双参数化间隔支持向量机[14]和具有高斯样本不确定性的支持向量机（SVM with Gaussian sample uncertainty，SVM-GSU）[26]的启发。提出了一个新的不确定数据的双参数化间隔支持向量机模型，称为鲁棒双参数化间隔支持向量机（robust twin parametricmargin support vector machine，R-TPMSVM）。该方法的任务是针对正类样本点和负类样本点分别寻找一个相应的参数化间隔超平面，并不要求这两个超平面平行。由于鲁棒双参数化间隔支持向量机通过求解两个较小规模的优化问题，使得它具有更好的训练效率。此外，在鲁棒双参数化间隔支持向量机中，假设每个样本点都服从多元高斯分布，从而得到的不确定区域比固定超球或超椭球形式的不确定区域[21-22]更加灵活。最后，针对优化问题，提出了有效的随机梯度下降（stochastic gradient descent，SGD）算法。分别考虑了人工数据集、六个基准数据集和威斯康辛乳腺癌数据集等，实验数据数值结果表明，鲁棒双参数化间隔支持向量机具有较好的泛化能力。

1 研究背景

本章将简要介绍双参数化间隔支持向量机[14]。考虑以下二分类训练集：

其中，(xi,yi)是第i个样本点，xi∈Rn是输入，yi∈{+1,-1}是输出，i=1,2,…,l，l是样本点的个数。为了方便起见，记向量,i=1,2,…,l1和,j=1,2,…,l2分别表示正类样本点和负类样本点的输入，并且令l1和l2分别为正类样本和负类样本的个数，显然有l=l1+l2。

对于线性情形，双参数化间隔支持向量机的任务是寻找如下两个非平行超平面：

事实上，式（2）和（3）分别确定了正类参数化间隔超平面和负类参数化间隔超平面。

为了得到参数化间隔超平面（2）和（3），考虑如下一对无约束优化问题：

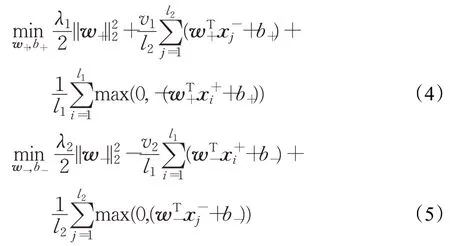
其中，λ1,λ2,v1,v2是非负参数，并且和是损失项。

若得到优化问题（4）和（5）的解w+,b+,w-,b-，对一个新的样本点x∈Rn，可由以下决策函数进行判别：

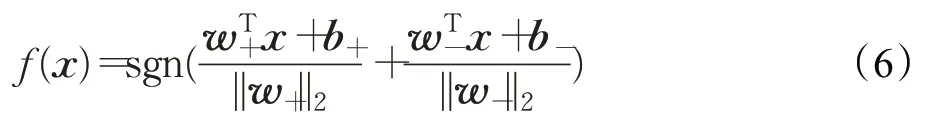
2 鲁棒双参数化间隔支持向量机

2.1 建立优化模型

在本节中，针对带不确定区域的二分类问题，提出了鲁棒双参数化间隔支持向量机。对于带服从多元高斯分布不确定区域的训练集如下所示：

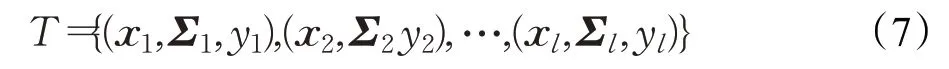
其中，第i个样本点(xi,Σi,yi)服从多元高斯分布，xi∈Rn表示输入的均值向量，为输入的协方差矩阵，yi∈{±1}是类标签，i=1,2,…,l。为了方便起见，用=1,2,…,l1表示正类样本点的输入，j=1,2,…,l2表示负类样本点的输入，且l=l1+l2。假设随机向量。

现在，任务是分别针对正类样本和负类样本寻找如下两个参数化间隔超平面：

分别称式（8）为正类参数化间隔超平面，式（9）为负类参数化间隔超平面。事实上，假设正负类参数化间隔超平面将训练集式（7）中的样本点正确分离当且仅当：

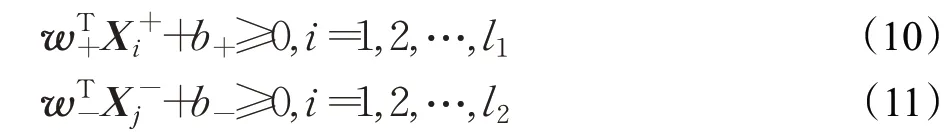
为此，构造如下一对优化问题：

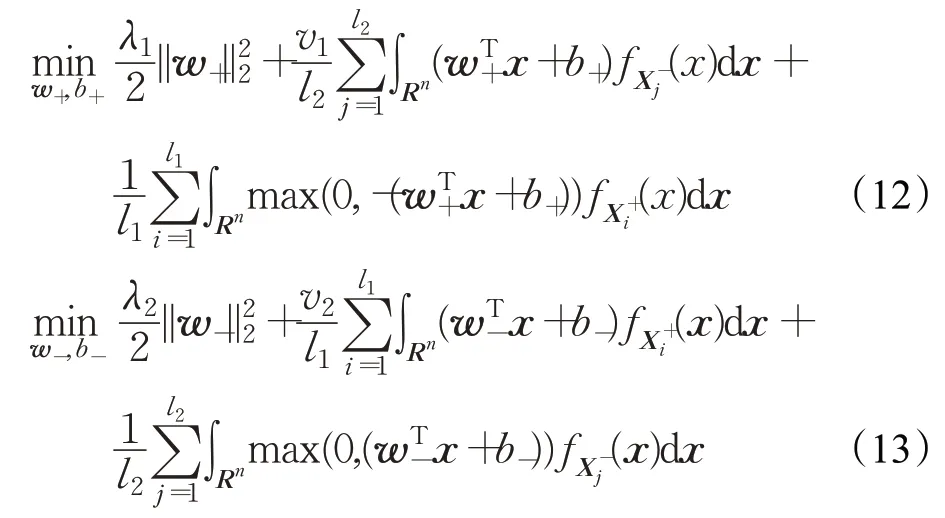
其中，λ1，λ2＞0 是正则化参数，v1,v2＞0 是惩罚参数。并且

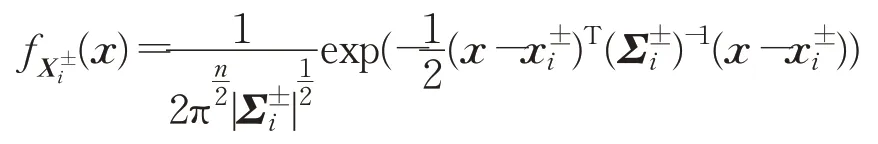
是第i个随机向量的高斯概率密度函数（PDF）。

值得一提的是，在优化问题（12）中，第一项是正则项，控制优化问题的复杂度；第二项是使负类样本尽可能远离正参数化间隔超平面；第三项是正例类样本点被正类参数超平面错误分类的损失。对于优化问题（13），有类似的解释。图1 显示了双参数化间隔支持向量机和鲁棒双参数化间隔支持向量机的几何直观图。

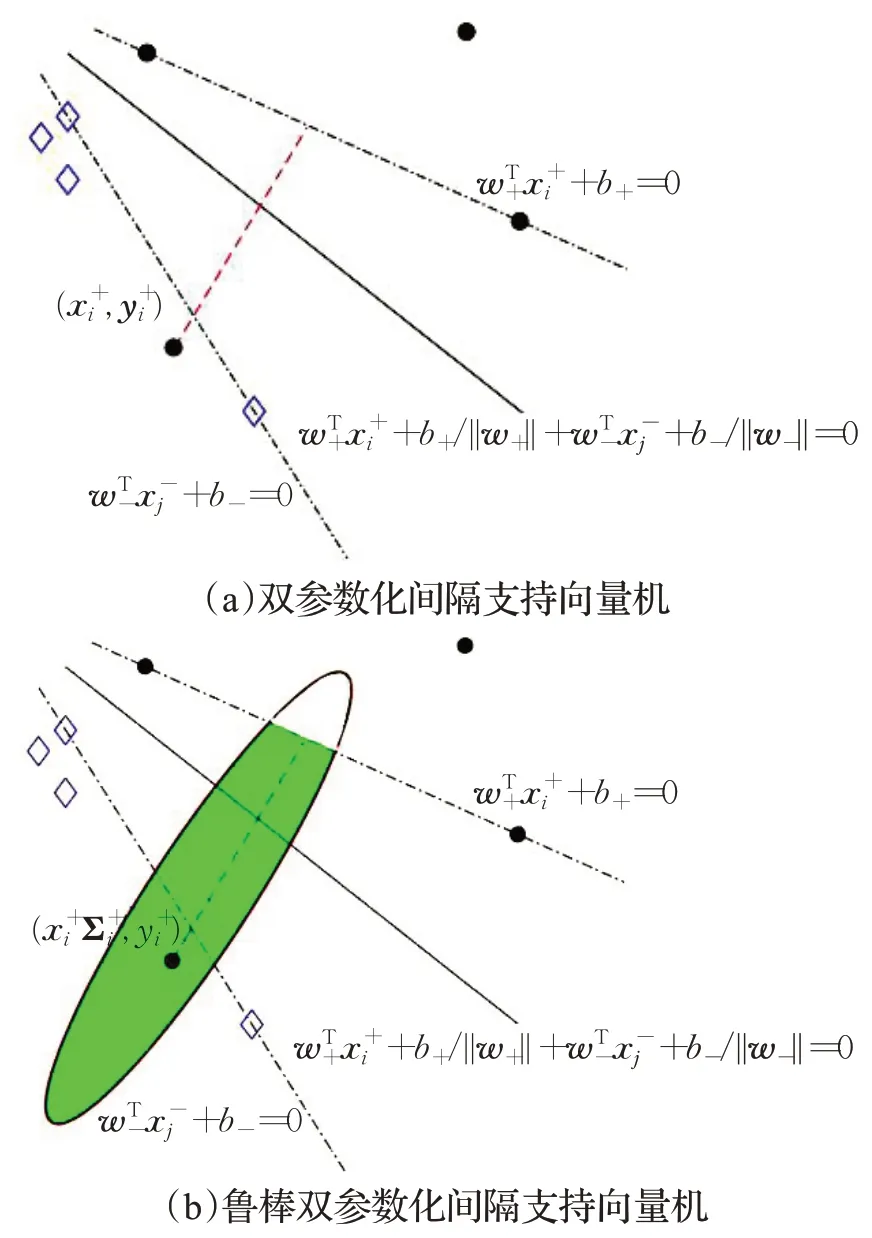
图1 双参数化间隔支持向量机和鲁棒双参数化间隔支持向量机的几何直观图Fig.1 Geometric intuitions of twin parametric-margin support vector machine and robust twin parametric-margin support vector machine

2.2 优化模型的求解

现将优化问题（12）的目标函数写作：

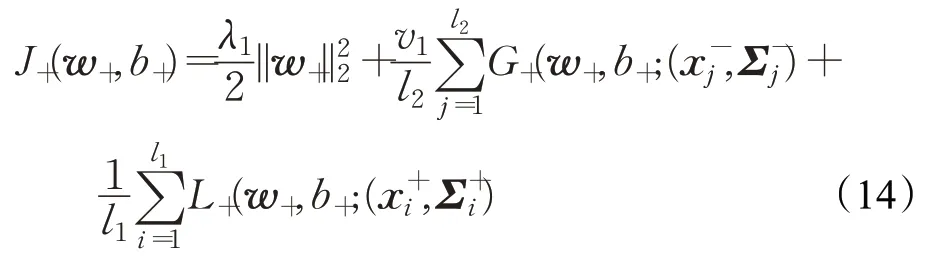
其中，针对第j个负类样本（即第j个高斯函数）投影函数为：

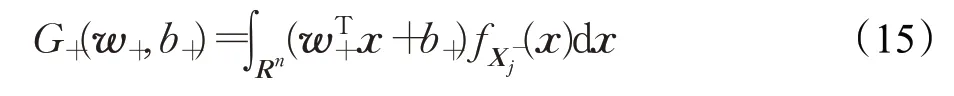
针对第i个正类样本（即第i个高斯函数）损失函数为：

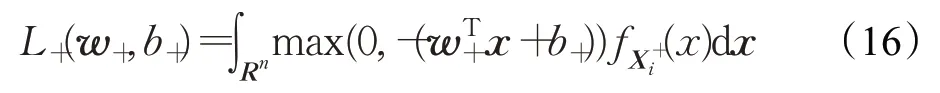
为了求解优化问题式（12），将使用随机梯度下降（SGD）算法。现在分别给出目标函数式（14）中的第二项和第三项的封闭形式。具体地，式（15）和式（16）分别可转化为：

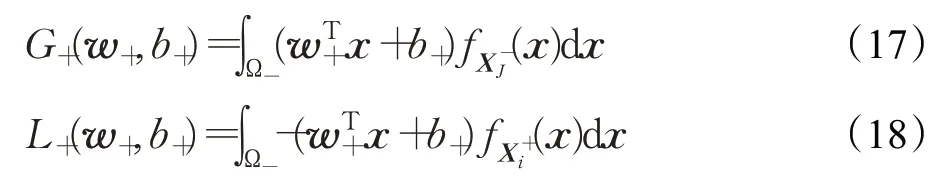
借用以下[26]定理：

定理假设随机向量x∈Rn服从多维高斯分布，其中均值为μ∈Rn，协方差矩阵为，其概率密度函数为：

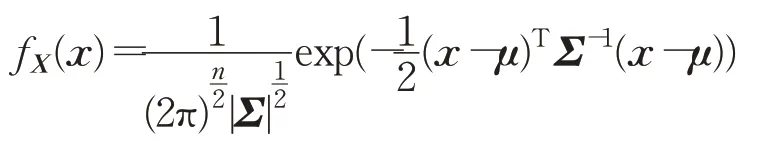
超平面H:aTx+b=0 将Rn空间分为两个半空间，即Ω±={x∈Rn:aTx+b＞或＜0},Ω+∪Ω-=Rn且Ω+∩Ω-=φ且积分I±:Rn×R→R，定义为：

则有：

其中，dμ=aTμ+b和。

由定理可知，对于半空间：

Ω-={x∈≤0},积分式（15）可转化为如下的闭式：

现分别对J+关于w+和b+求偏导数，可得：

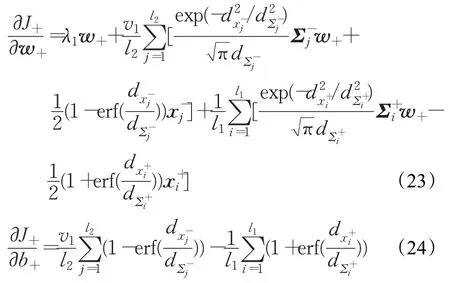
类似地，优化问题式（13）的目标函数可以表示为：

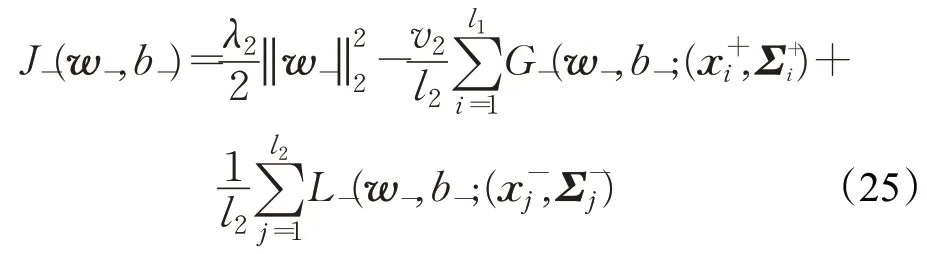
其中

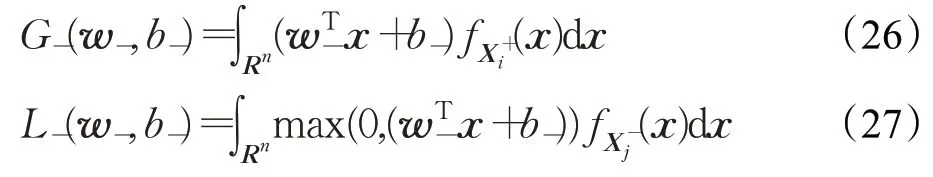
同理，上两式所示的积分可表示为：

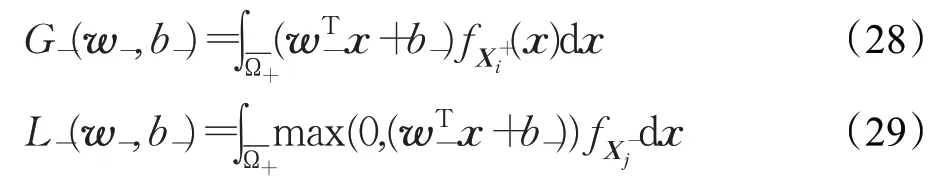
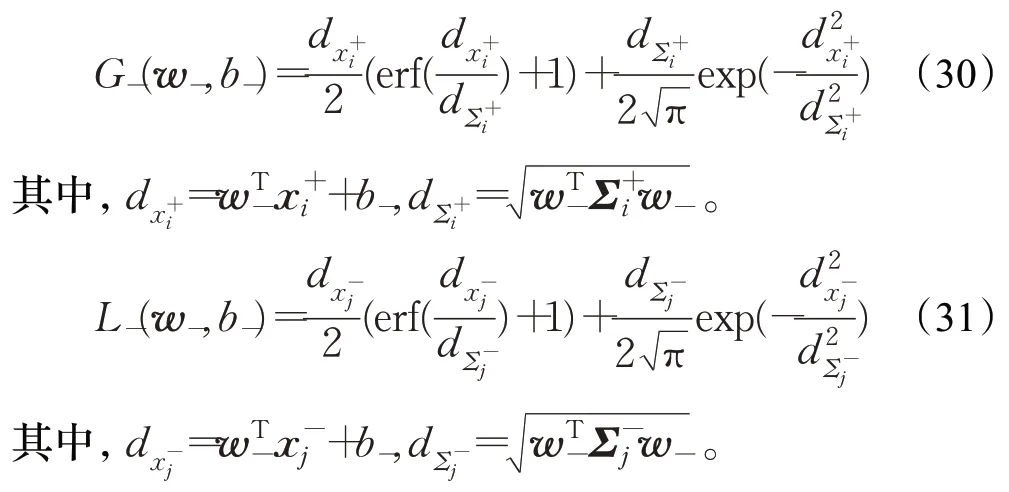
现对目标函数式（25）分别关于w-和b-求偏导数，可得：

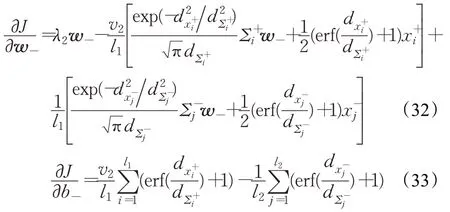
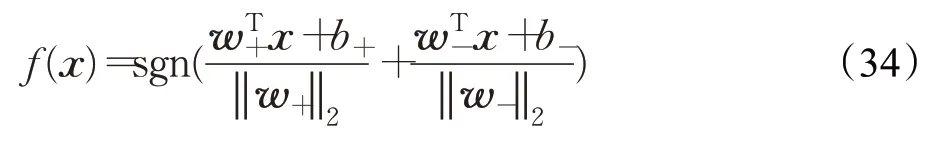
2.3 算法实施步骤

接下来，给出优化问题式（11）和（12）的求解算法。受Pegasos 算法[30]的启发，提出了一种求解鲁棒双参数化间隔支持向量机的随机梯度下降算法。为了方便表示，对于训练集T（式（7）），令T=T++T-，其中集合T+包含所有正类样本点，集合T-包含所有负类样本点。该算法的输入参数如下：（1）迭代次数Γ，（2）用于计算次梯度的正样本个数和负样本个数为k1和k2。对于初始值，设置任意的向量。第t次迭代，随机地选取T+和T-的子集，它们的势分别为k1和k2，即，其中=k1，。与此同时，设置迭代速率。可得优化问题式（14）和（25）的近似表达式：

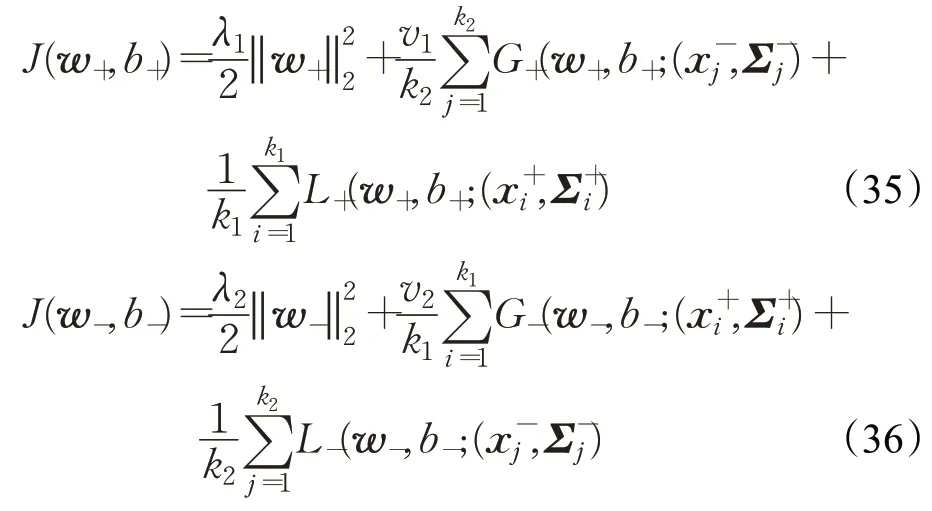
迭代更新步骤：

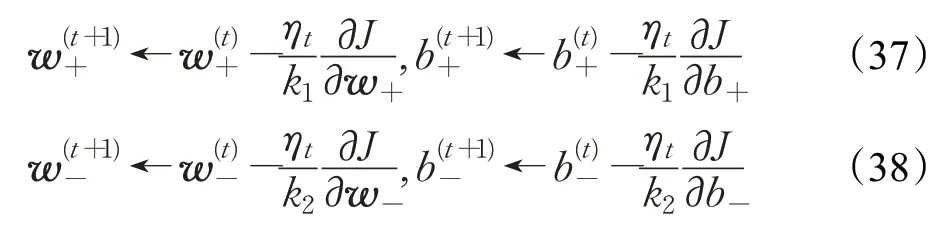
其中，一阶偏导数由式（23）、（24）和式（32）、（33）给出，并要求分别投影到半径为和[31]的超球中，即

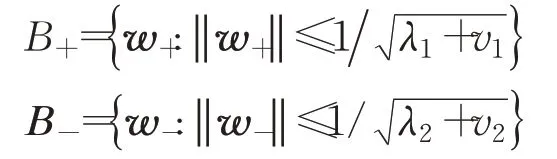
算法1随机梯度下降求解方法

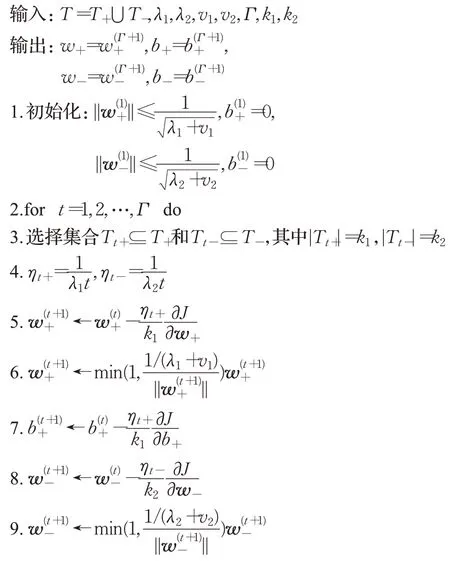
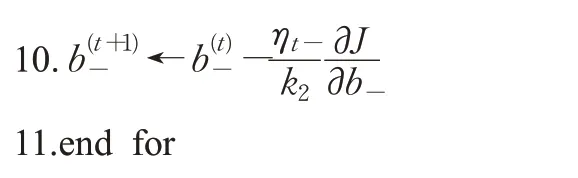
3 数值实验

在这一章中，为了说明提出的鲁棒双参数化间隔支持向量机的性能，将其在二维人工数据集、六个基准数据集和威斯康辛乳腺癌数据集进行了数值实验。所有的代码都是在MATLAB2015b 环境下完成的。硬件设备指标：Intel Core I5 CPU，4 GB内存。为了简化参数选择的复杂性，令λ1=λ2，v1=v2，并分别在集合{2i|i=-8,-7,…,2}和集合{1，2，3，4，5，6}中选择最优参数，并使用10折交叉验证的方式搜寻最优参数。

3.1 人工数据集

为了展示鲁棒双参数化间隔支持向量机的几何直观，构造了一个二维数据集，如图2所示，三个负类样本点用红色的“×”表示，三个正类样本点用绿色的“+”表示。假设每一个训练样本的不确定性由协方差矩阵给出，即每个样本点服从二维高斯分布。图2（a）和图2（b）直观地显示了传统双参数化间隔支持向量机（TPMSVM）和鲁棒双参数化间隔支持向量机（RTPMSVM）的分划超平面。从图2（a）不难发现，传统双参数化间隔支持向量机只能将六个点正确分类，而图2（b）显示鲁棒双参数化间隔支持向量机不仅能将六个点正确分类，而且还可以将相应的不确定区域也正确地分类。这是因为传统的双参数化间隔支持向量机忽略了数据的不确定区域。

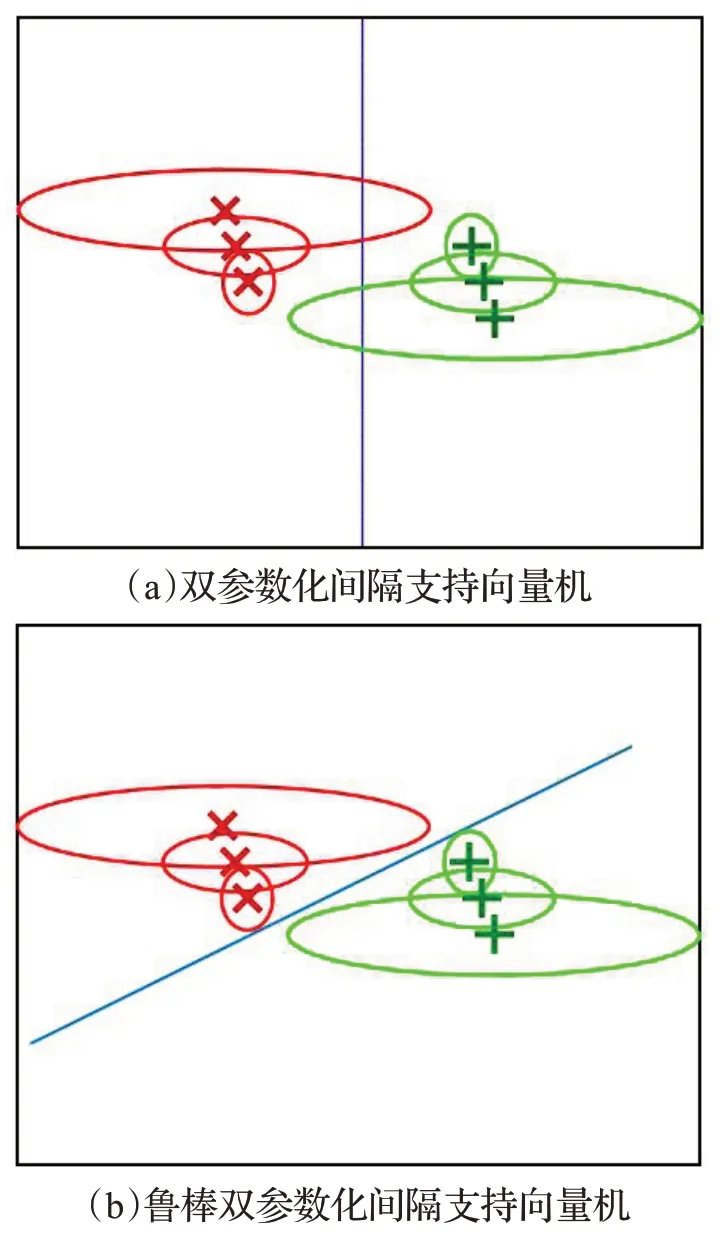
图2 两种方法的几何直观Fig.2 Geometric intuition of two methods

3.2 基准数据集

在本节中，将在以下六个基准数据集[32]上评估鲁棒双参数化间隔支持向量机，分别是Hepatitis、WPBC、HStatlog、Heart-c、Bupa Liver 和Votes。六个数据集的详细信息展示在表1，包括样本个数、属性个数和所占类别比例。这些数据集都是二分类问题。对于有缺失值的数据集，用零填补。与文献[22]中使用的数据集相同，并且采用了与文献[22]相同的数据预处理方法。

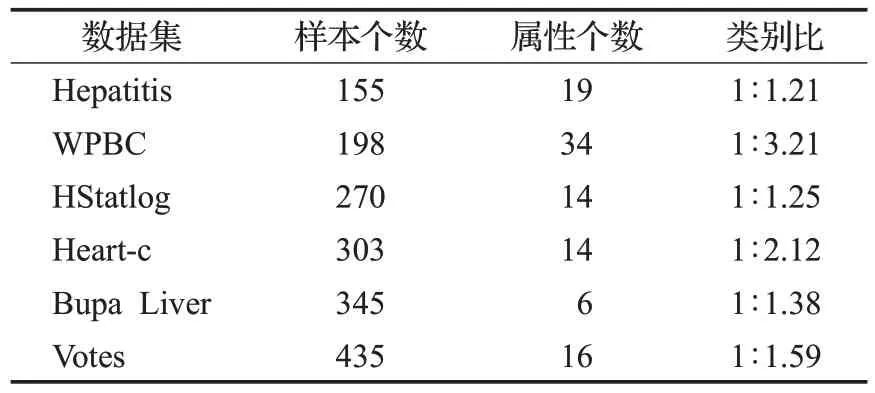
表1 六个基准数据集简介Table 1 Introduction to six benchmark datasets

将鲁棒双参数化间隔支持向量机与如下五种方法进行了对比：鲁棒支持向量机（R-SVM）[18]、鲁棒双支持向量机（R-TWSVM）[22]、高斯样本不确定支持向量机（SVM-GSU）、双支持向量机（TWSVM）[13]、双参数化间隔支持向量机（TPMSVM）[14]。首先，考虑简化后的不确定区域，即每个样本的不确定区域固定为一个半径为r的超球体。对于鲁棒双参数化间隔支持向量机，只需要为每个样本xi∈Rn，构造各向同性协方差矩阵Σi=(r,r,…,r)n，假设其在95%的置信度水平。表2中的前三个方法的数值结果来自于文献[22]。在这六个基准数据集上执行了双参数化间隔支持向量机（TPMSVM），高斯样本不确定支持向量机（SVM-GSU）和鲁棒双参数化间隔支持向量机（R-TPMSVM），结果见表2。表现较好的结果用黑体表示。从表2可以看出，鲁棒双参数化间隔支持向量机在四个数据集具有较好的性能。值得注意的是，本文提出的方法是线性分类器，并不需要使用核函数。

此外，图3 对比了鲁棒双参数化间隔支持向量机（R-TPMSVM）和高斯样本不确定支持向量机（SVMGSU）在六个基准数据集上的训练时间。显然地，除了威斯康辛（WPBC）数据集之外，鲁棒双参数化间隔支持向量机所花费的时间小于高斯样本不确定支持向量机所花费的时间。也可以注意到对于较大的数据集，本文的方法在时间上有更多的优势。

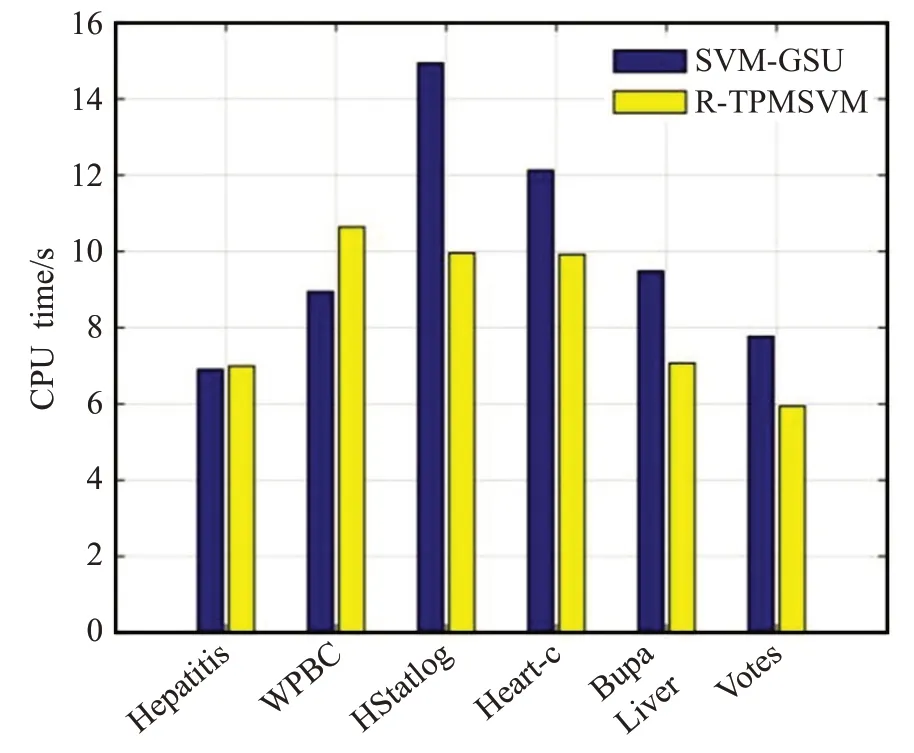
图3 两种方法训练时间的对比Fig.3 Comparison of training time between two methods

不难发现，表2 中的结果只考虑了一种特殊情况，具有各向同性协方差矩阵的不确定区域。但鲁棒双参数化间隔支持向量机可应用于更一般的情况。借用文献[33]中三种方法和文献[34]中的方法构造协方差矩阵。由于六个基准数据集中数据并没有重复采样，需要构建均值向量和协方差矩阵，从而得到形如训练集式（7）所示的样本点。具体地，假设数据集中的观测数据点xi为均值向量。接下来，需要构造协方差矩阵。假设协方差矩阵是对角阵，即。对每一个属性之间相互独立的数据集来说，对角元素,p=1,2,…,n是各不相同的。

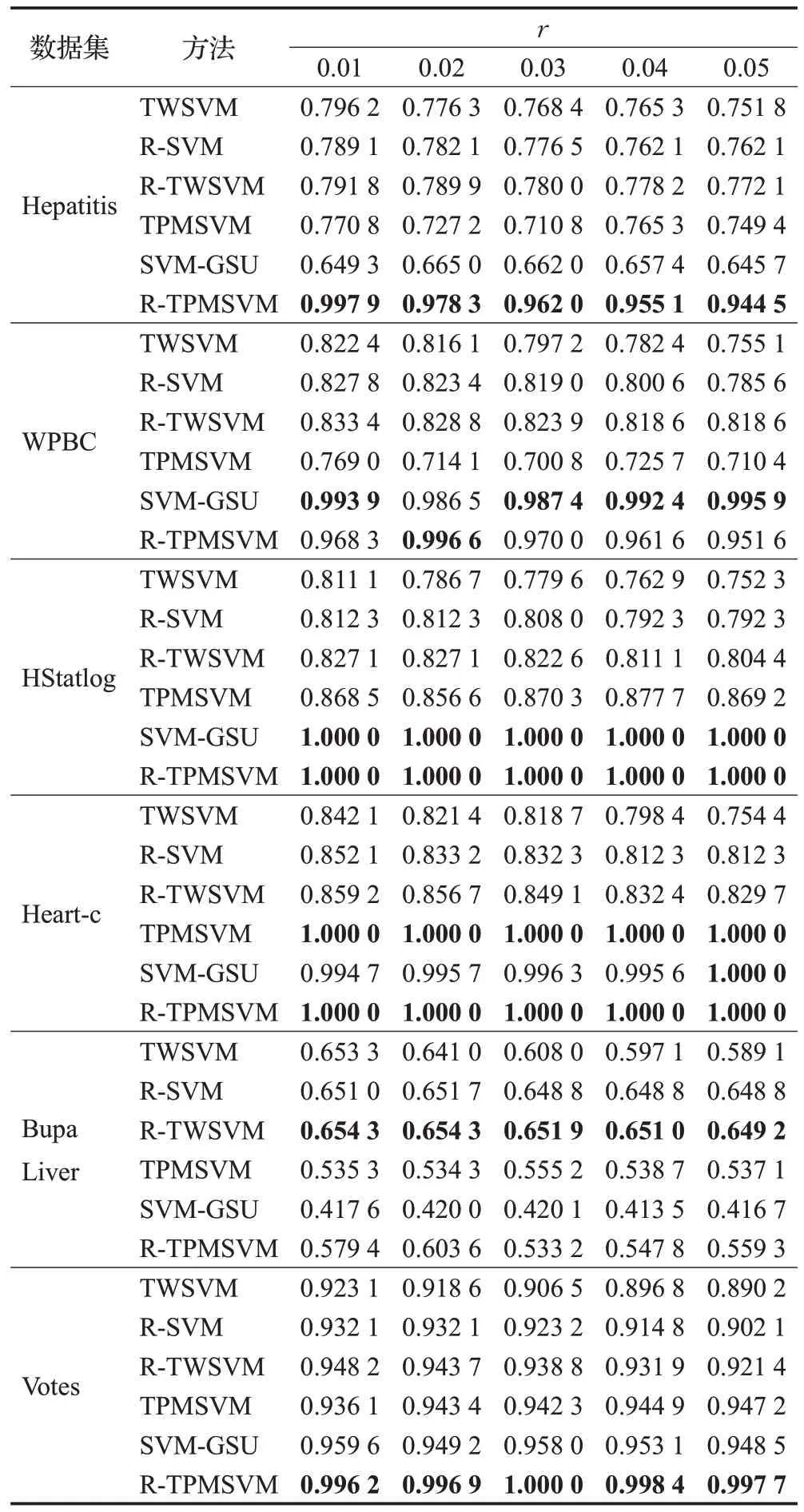
表2 六种方法在基准数据集上的准确率对比Table 2 Accuracy comparison of six methods on benchmark datasets

具体地说，用l个数据点的属性观测范围计算协方差矩阵。用以下四种方法构造协方差矩阵，将这四种协方差矩阵分别记作Σ1、Σ2、Σ3、Σ4。

第一种构造协方差矩阵的方式：

其中对角线元素为：

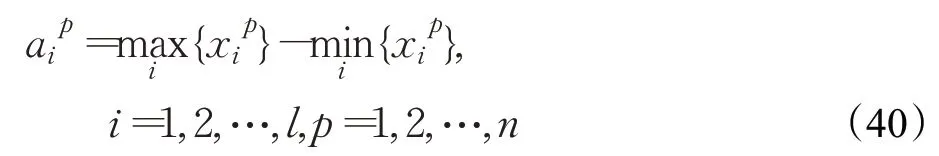
第二种构造协方差矩阵的方式：

其中对角线元素为：

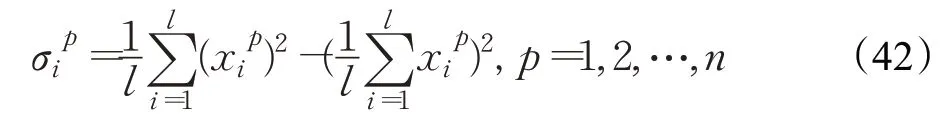
第三种构造协方差矩阵的方式：

其中对角线元素为：

第四种构造协方差矩阵的方式：

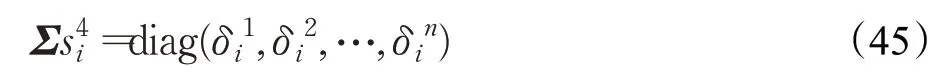
其中，对角线元素为：

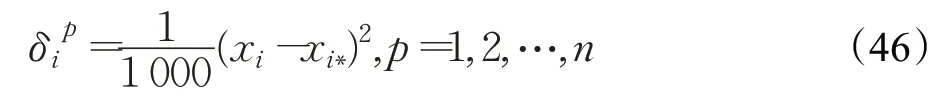
其中，xi*取自于与xi不同类的样本点中距离xi最近的样本点。需要说明的是，前三种构造方式使得每个样本点具有相同的协方差矩阵，只是协方差矩阵的对角线元素各不相同。而第四种方式，使得每个样本具有不同的协方差矩阵。

表3给出鲁棒双参数化间隔支持向量机（R-TPMSVM）和高斯样本不确定支持向量机（SVM-GSU）对应于四种协方差矩阵的结果，包括准确率和训练时间，表现较好的结果用黑体表示。从表3可以看出，虽然鲁棒双参数化间隔支持向量机使用前三种构造协方差矩阵的准确率不高于高斯样本不确定支持向量机，但是本文方法的训练时间小于高斯样本不确定支持向量机。值得注意的是，本文方法使用第四种构造协方差矩阵的准确率都高于高斯样本不确定支持向量机，训练时间也较有优势。四种协方差的构造方式，可根据不同需要来进行灵活选择。

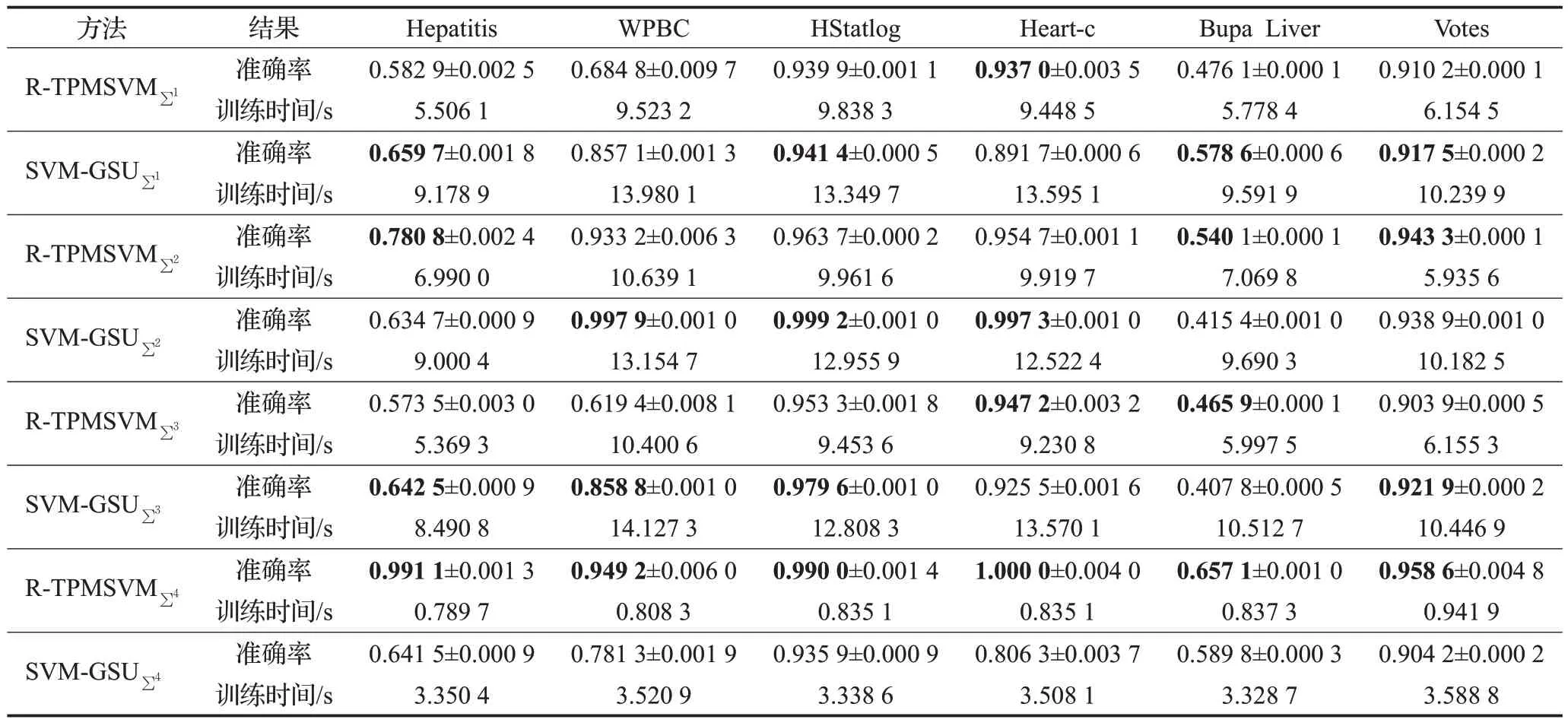
表3 四种协方差矩阵的训练时间及准确率对比Table 3 Comparison of training time and accuracy of four covariance matrices

为了考虑参数对算法的影响，图4展示了不同参数下鲁棒双参数化间隔支持向量机的准确率的变化情况。令正则化参数λ=λ1=λ2，惩罚参数v=v1=v2，当固定其中一个参数，调节另一个参数，这样可以观察出鲁棒双参数化间隔支持向量机的准确率与参数的依赖关系。图4（a）给出了当惩罚参数v固定，正则化参数λ在集合{2i|i=-8,-7,…,2}中取不同的值时准确率的变化。图4（b）给出了当正则化参数λ固定，惩罚参数v在集合{1，2，3，4，5，6}中取不同的值时准确率的变化。可以看出，鲁棒双参数化间隔支持向量机在六个基准数据集上随着参数的变化，准确率变化缓慢。即参数的选取对准确率影响不大。

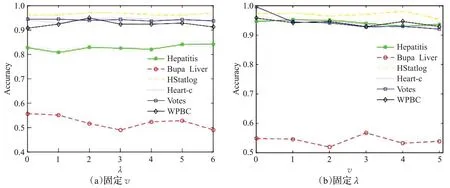
图4 不同参数下的准确率变化情况Fig.4 Accuracy changes under different parameters

3.3 威斯康辛乳腺癌数据集

威斯康辛乳腺癌数据集（WDBC）[32]采集了患者乳腺肿块，得到了经过细针穿刺（FNA）后的数字化图像，并对这些数字图像进行了特征提取，这些特征描述的是图像中的细胞核，肿瘤分为良性和恶性。即该数据集569 个样本中，包含恶性（212 个样本）和良性（357 个样本）两类样本。对于威斯康辛乳腺癌数据集，使用与文献[26]相同的预处理方式。即对每一幅图像进行相应的特征计算，得到30 个特征值。（包括10 个特征的三个维度：平均值、标准差和最大值）。每个特征值保留4位数字，数据中没有缺失值。每个样本均值x=(x1,…,x10,s1,…,s10,w1,…,w10)T∈R30，其中xj表示均值，sj表示标准误差，wj表示第j个特征的最大值，j=1,2,…,10。由于标准误差si和方差有关系式，其中的样本大小N是未知的。记每个输入的协方差矩阵为，其中被设置为很小的常数（比如，10-6），表示此特征对于这个方向的不确定性非常小，而其余的方差通过位于标准差范围内并控制在均值的80%内缩放得到。

表4给出了鲁棒双参数化间隔支持向量机与几个方法的准确率，包括线性支持向量机（LSVM）[4]、功率支持向量机（PSVM）[35]、各向同性支持向量机（LSVM-iso）[22，25]、高斯样本不确定支持向量机（SVM-GSU）[26]、双参数化间隔支持向量机（TPMSVM）[14]。前四种方法的结果来自文献[35]。这里随机地将数据集分为10份，其中90%作为训练集，10%作为测试集，最优参数由十折交叉验证确定。本文方法的准确率结果是10次实验结果的平均值。从表4明显可以看出，鲁棒双参数化间隔支持向量机表现最好。

表4 几种方法在威斯康辛乳腺癌数据集上的准确率比较Table 4 Comparison of accuracy of several methods on Wisconsin breast cancer dataset

4 结论

本文提出了鲁棒双参数化间隔支持向量机，为此设计随机梯度下降（SGD）算法来求解相应的优化问题。通过引入非平行边界超平面的思想，提出的鲁棒双参数化间隔支持向量机比高斯样本不确定支持向量机更稳定。鲁棒双参数化间隔支持向量机通过求解一对较小规模的优化问题，因此具有较快的训练速度。在鲁棒双参数化间隔支持向量机中，由于不同的点对应不同的协方差矩阵，考虑了更灵活的不确定区域。在人工数据集、基准数据集和威斯康辛乳腺癌数据集上的数值实验表明，该方法具有较好的泛化性能。