基于布谷鸟迭代更新策略的多重优化算法

丁希成，王红军

国防科技大学 电子对抗学院，合肥230000

群智能算法作为新兴智能优化算法之一，由于其稳定性、并行性、鲁棒性和自组织性等特点而被广泛地应用于计算机、农业和商业等领域来实现求解最优化。自1989年Beni等在元胞机器人系统中首次提出了群智能的概念[1]，目前被广泛认可的群智能算法有遗传算法（genetic algorithm，GA）、蚁群算法（ant colony optimization algorithm，ACOA）、粒子群算法（particle swarm optimization algorithm，PSOA）、蛙跳算法（shuffled frog leading algorithm，SFLA）、布谷鸟算法（cuckoo search algorithm，CSA）和灰狼算法（grey wolf optimizationalgorithm，GWOA）等。

布谷鸟算法作为一种新型的群智能算法，自2009年Yang 等[2]提出以来，由于其参数少、全局搜索能力强等特点受到众多学者的青睐，被应用于各类最优化问题的求解[3-6]，布谷鸟算法的核心优势就是采用莱维（Levy）飞行来产生运动轨迹，其高度随机的飞行机制使得搜索可以快速地在迭代前期遍布解空间，种群具有更好的多样性，但是也导致算法在后期针对局部的开发能力较差，收敛速度较慢。因此，近年来众多学者依据其特性对布谷鸟原始算法进行了如下三个方面的改进：参数的自适应调整，算子修改、增加和替换，以及融合其他算法。

文献[7]根据种群每次迭代后适应度的差别分为三个阶层，每个阶层采用不同的飞行步长，并引入随机偏移算子动态调整迭代方程，但算法复杂度略高。文献[8]将多种群粒子群算法结合布谷鸟算法，并采用中位数聚类的方法将相近层次的种群聚类以加快收敛速度，但对多峰函数的搜索精度仍有待加强。文献[9]根据种群历史最优适应度和自身最优适应度按比例减少种群数量，提出了一种参数自适应的布谷鸟算法，但会导致后期搜索能力下降。文献[10]通过改进布谷鸟搜索的步长和发现外来物种的概率，提高了粒子滤波算法中粒子的多样性，保证了估计精度。文献[11]将布谷鸟算法融合进粒子群算法，并改进了算法的拓扑结构，平衡了算法的全局搜索能力和局部开发能力，但在后期小范围内的多峰情况难以收敛到最优值。文献[12]将混沌映射引入布谷鸟算法的种群初始化中，提高了寻优的速度和精度。文献[13]混合布谷鸟算法和遗传算法，引入交叉变异策略，增强种群的多样性，但收敛精度仍有待提高。文献[14]将改进的自适应布谷鸟算法应用于分布式无人机部署上，取得良好的效果，但在搜索后期的局部开发能力都仍需进一步加强。文献[15]将tent映射引入灰狼算法，并借鉴粒子群算法思想，提出了混合灰狼优化算法，进一步提高了灰狼算法的收敛速度和精度，但跳出局部最小值的能力有待加强。文献[16]通过自适应策略调整动态步长和发现概率，提高了布谷鸟算法收敛速度和精度，但同样存在陷入局部极值问题。文献[17]利用多阶段动态扰动策略增加了种群的多样性和粒子位置的灵活性，但无法保证初始种群的合理性。

本文基于CS算法和GWO算法的优势，从布谷鸟算法的迭代更新策略出发，引入粒子群思想，并利用灰狼算法的狩猎思想，在搜索后期进行小范围扰动式搜索，提高算法后期小范围扰动，促使算法在保证搜索广度的前提下，利用粒子间学习增加其种群内自我认知和种群间社会交流的能力。同时引入tent 映射方法使初始种群更均匀地遍布解空间，防止搜索过程陷入局部最优，提高种群收敛速度。同时，针对布谷鸟参数固定的弊端，对步长控制参数提出对数自适应改进策略，提高算法的全局搜索能力和局部开发能力。

1 经典布谷鸟算法描述

布谷鸟算法是一种启发式群智能优化算法，通过模拟自然界布谷鸟寻找鸟巢繁殖后代的行为，总结其规律运用到最优化问题解决上来。布谷鸟算法在模拟寻找鸟巢的过程需要遵循以下三条假设规则：

（1）每只布谷鸟每次只孵化一枚鸟蛋，并选择一个随机鸟巢进行孵化。

（2）在所有寄生巢中选择最好的寄生巢保留至下一代。

（3）在布谷鸟飞行过程中，可利用的鸟巢总数n固定，一个鸟巢中布谷鸟鸟蛋被主人发现并抛弃的概率为Pa∈[0,1]。

在布谷鸟原始算法中，布谷鸟的种群规模代表解决方法的数量，通过Levy 飞行共同寻找搜索空间内的最优鸟巢。鸟巢的位置更新方程为：

其中，α为步长缩放因子，通常取固定常数0.01；⊕为点对点的乘法；莱维飞行通常采用Mantegna算法实现，其步长s表示为：

其中，s为莱维飞行的步长，β取1.5，u、v为服从正态分布的随机数：

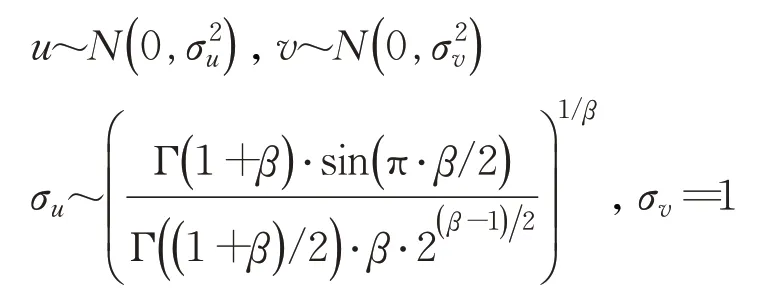
鸟巢位置通过莱维飞行更新后，判断随机数r∈[0,1]和Pa的大小，取Pa=0.25,则有：若r＞Pa，则按照式（4）更新，否则不更新鸟巢位置。

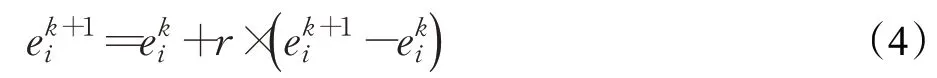
2 算法改进

2.1 参数α 的对数自适应改进

布谷鸟算法主要由莱维飞行随机搜索和抛弃原有鸟巢随机替代两部分组成，并结合择优选择的原则迭代更新。根据式（2），参数α对于莱维飞行的步长控制具有重大的影响。

在寻优算法中，通常希望在搜索前期，通过较大的步长以扩大搜索范围，增加种群多样性和全局探索能力，在搜索后期，将步长稳定在较小值以提高局部搜索能力。但在原始布谷鸟算法中，参数α通常被设置为常数0.01，无法满足在不同搜索阶段的搜索需求，为此，本文提出了一种针对参数α的对数自适应改进，其计算公式为：

其中，maxgen为最大迭代次数，t为当前迭代次数。使参数α随着算法搜素进程动态从0.5下降到0.001，相比于固定常数，前期更大的搜索步长和后期更小的搜索步长，有利于提高收敛速度和搜索精度。

2.2 Skew tent映射初始化种群

布谷鸟算法在求解函数优化的问题时，通常采用随机初始化种群的方法，这种方法难以确保初始参数均匀遍布解空间，会导致算法的收敛速度减慢，同时也容易陷入局部最优解。而混沌运动因为具有随机性、遍历性和规律性等特点，可以使初始种群更均匀地遍布解空间，目前已广泛地在粒子群、灰狼、人工蜂群等群智能算法中以提高算法的搜索效率。

本文采用Skew tent 混沌映射，相对于目前普遍使用的logistic映射，减少了在边缘区域分布率高的问题，其均匀性更好。

Skew tent算法公式为：

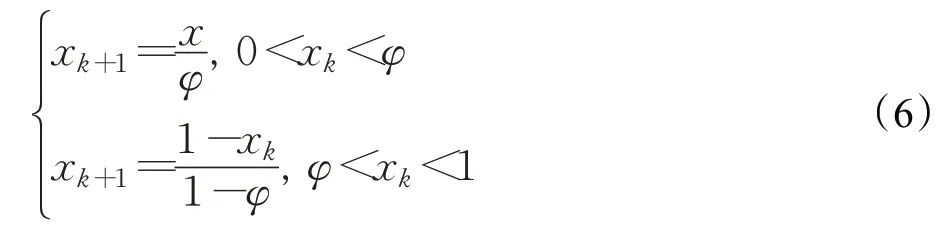
其中，φ∈[0,1]，取φ=0.5，x∈[0,1]。

2.3 迭代方程更新

经典布谷鸟算法由于其飞行轨迹的高度随机性，在迭代后期收敛的速度和精度效果均不够理想，由式（2）～（4）可知，布谷鸟算法每次迭代采用的是随机迁移和贪婪策略，种群中始终只保持全局最优个体作为引导者，这容易导致算法对其他优异解的区域探索能力下降。为了增强搜索的活力和效率，借鉴粒子群算法思想，加入“社会学习部分”和“自我学习部分”，其改进的位置更新公式为：

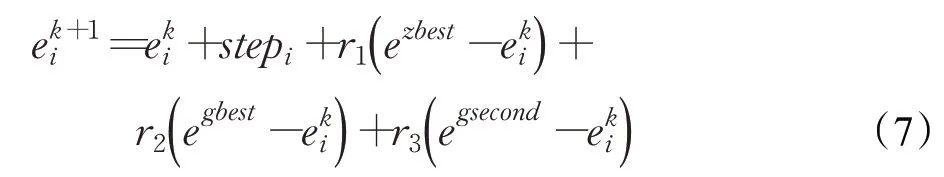
其中，stepi为莱维飞行的轨迹，ezbest为个体历史最优解，可以增强位置更新的自我学习的能力。egbest为全局历史最优解，egsecond为全局历史次优解，可以增强位置更新的社会学习能力。r1、r2、r3为学习因子。其中r1为针对个体历史最优解的学习因子，表示粒子的自我学习能力；r2和r3分别为针对全局历史最优解和全局历史次优解的学习因子，表示粒子的社会学习能力。三者均取[0,1]区间的随机数。

2.4 灰狼算法变异种群

为了进一步提高算法的收敛速度和局部搜索能力，本文借鉴灰狼算法中的α、β、δ狼狩猎机制，即领袖狼号召群体尽快靠近其周围达到快速种群快速收敛的目的。灰狼群体中的最优解为α，次最优解为β，第三最优解为δ，其他解均称为w，每次搜索过程中通过α、β、δ狼作为领袖狼包围猎物，其中猎物标记为头狼∝所在的位置，本文选用每次布谷鸟算法寻优后的全局历史最优解，全局历史次优解，个体历史最优解分别作为α、β、δ狼，依据灰狼算法对种群内其他解进行变异，灰狼算法的数学模型为：

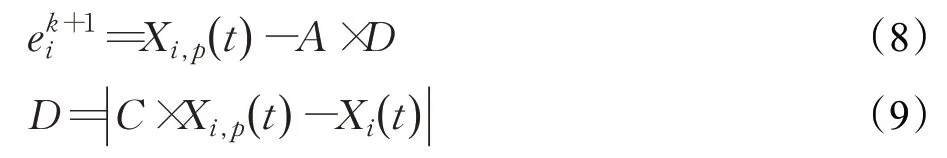
其中，Xi(t+1) 为第i个种群的w灰狼个体在t+1 次迭代时的位置，Xi,p(t)为第i个种群的领袖狼的位置，A×D为w狼包围猎物所移动的步长，A和C分别定义为：

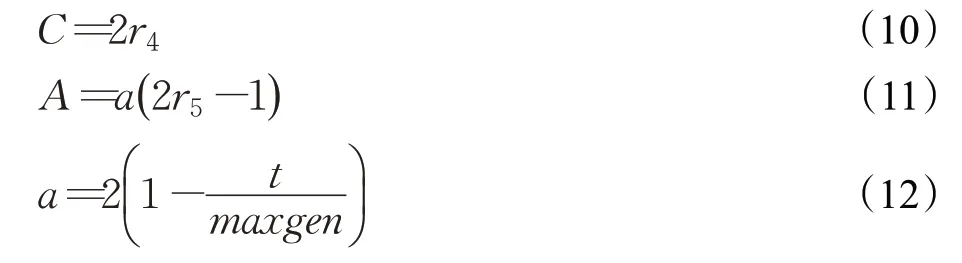
其中，r4和r5分别为0到1之间的随机数，A为距离收敛参数，随着迭代次数控制步长线性递减至0，C为0到2之间的随机数。

综合领袖α、β、δ狼，分别得到Xi,α、Xi,β和Xi,δ，并代入本文的算法：

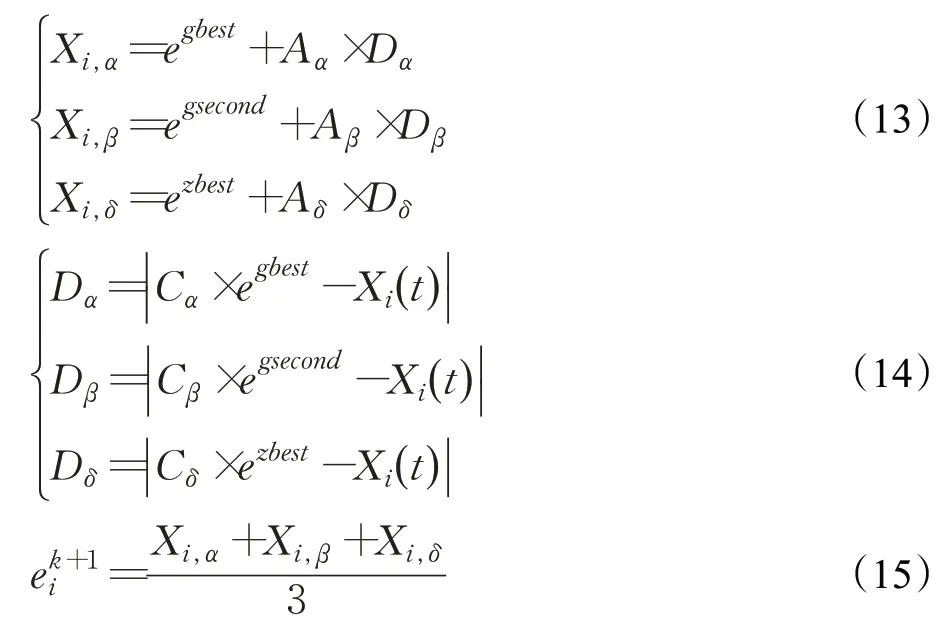
由式可以分别计算出三头领袖狼与ω狼位置距离参数，并通过式综合判断w狼的变异方向，确定变异后的位置。变异按照个体选取率确定种群的变异概率pc。

由灰狼算法原理可知，变异后的个体比变异前更接近领袖狼位置，可以使种群快速向领袖狼位置，即全局历史最优解，全局历史次优解和个体历史最优解逼近，达到快速收敛的目的。同时三头领袖狼也依然可以以ω狼的身份参与狼群的寻优，这是由于布谷鸟算法的贪婪策略，并不会使优异解退化，同时可以增加最优解附近的扰动，有利于提高布谷鸟算法的局部开发能力和加快其收敛速度。

2.5 混合优化算法架构

混合布谷鸟优化算法步骤如下：

步骤1算法参数设置：设置布谷鸟鸟巢数量N、搜索空间维数D、最大迭代次数maxgen和变异概率pc。

步骤2初始化种群：利用tent映射生成均匀分布搜索空间的初始种群。

步骤3计算各个鸟巢适应度值，并记录全局历史最优解，全局历史次优解，个体历史最优解的位置。

步骤4利用莱维飞行一组随机更新鸟巢位置，并重复步骤3。

步骤5根据式（7）保留或替换鸟巢位置，并重复步骤3。

步骤6利用灰狼算法思想变异种群，并重复步骤3。

步骤7循环迭代，并判断是否满足迭代终止条件。

步骤8输出最终的全局历史最优解egbest和对应鸟巢位置。

综上所述，可得混合布谷鸟优化算法架构如图1所示。

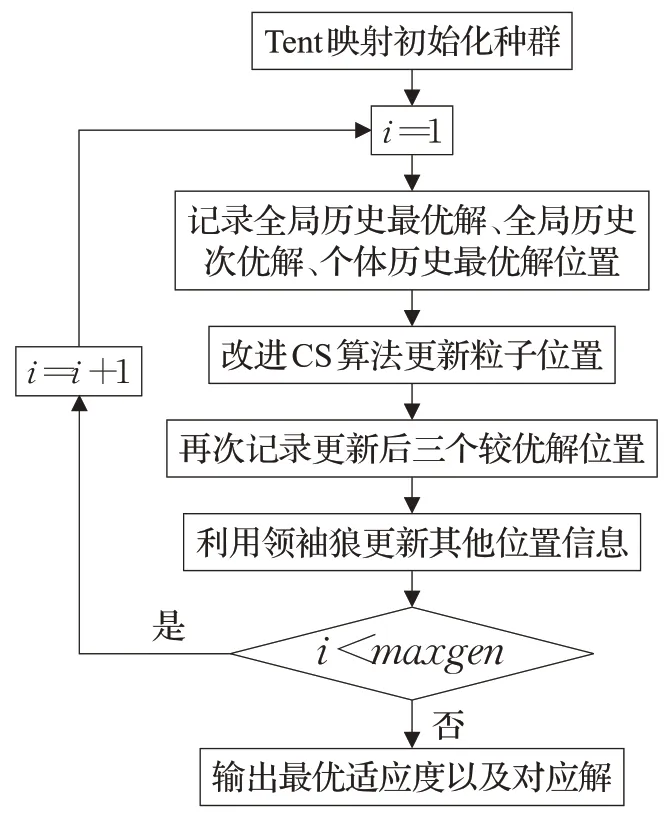
图1 算法流程图Fig.1 Algorithm flow chart

3 仿真实验分析

3.1 测试函数

为了验证本文所提出算法的先进性，选取了8个典型的beachmark测试函数，具体参数如表1所示。

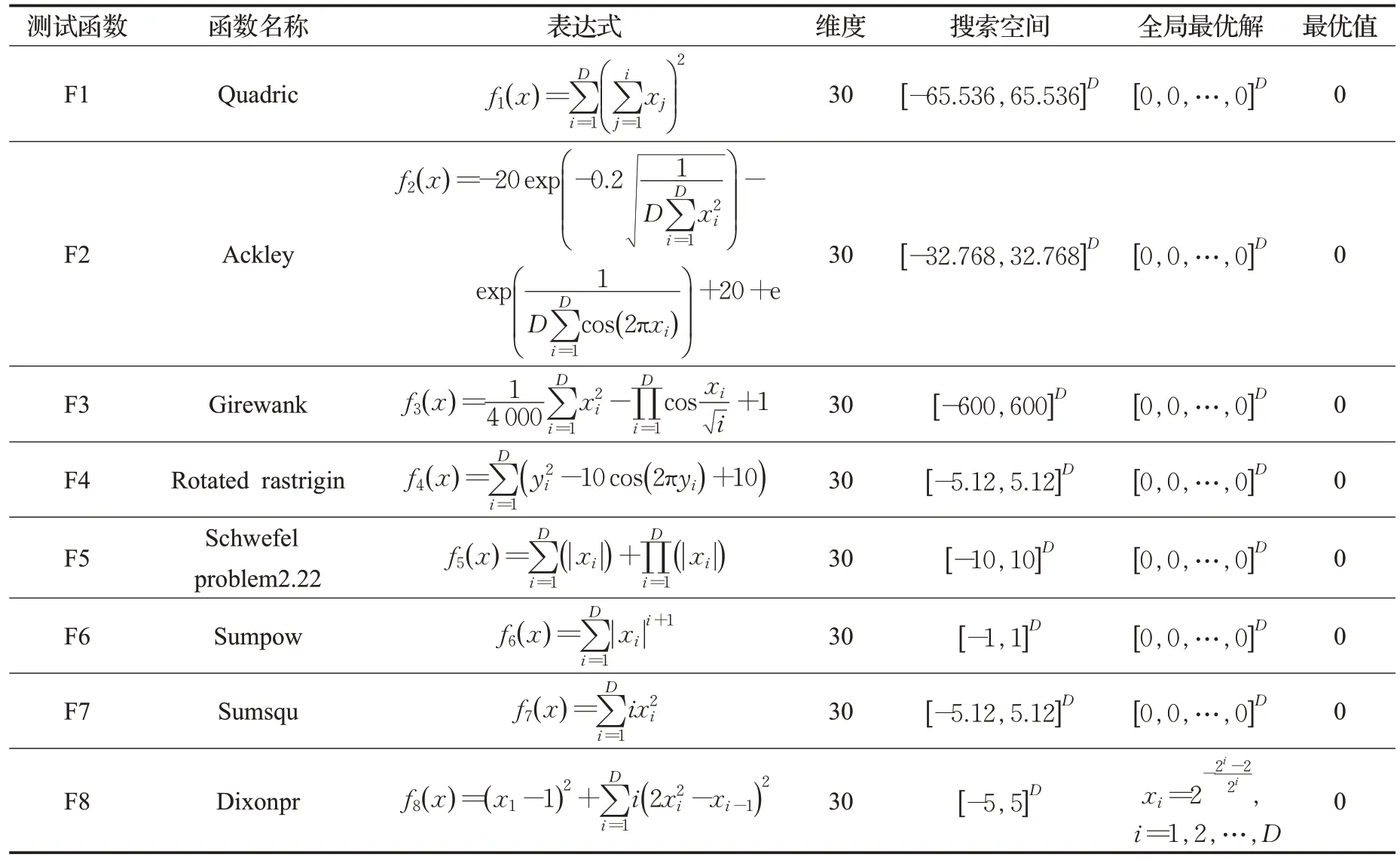
表1 Beachmark s测试函数参数Table 1 Parameters of beachmarks test function

其中测试函数F1、F2为典型的单峰测试函数，函数F1图像曲面较规则，函数F2图像为波浪状的倒沙漏型，具有非常多的局部极小值点和一个全局最小值点。函数F2、F3、F4 引入了三角函数项，因此函数图像存在规律性波动，使得算法寻优过程中会经历大量局部极小值。同时函数F4 在引入三角函数项基础上，在变量间引入乘项，使其互相影响，使得函数图像极其复杂，寻优难度极大。函数F5为幂和函数，函数F6为平方和函数，也称轴平行超椭球函数，均为典型的连续单峰的凸型函数，只存在一个全局极小值。函数F7 为较平缓的谷状函数，前期寻优速度快，但难以收敛到全局最小值。函数F8为波浪形的谷状函数，较函数F7更加复杂，更加考验算法的寻优能力。

3.2 算法参数

为了验证本文算法的性能，将布谷鸟算法、粒子群算法、灰狼算法与本文算法的寻优结果进行比较验证，其中各个对比算法的参数设置如表2。

表2 算法参数设置Table 2 Algorithm parameters setting

最大迭代次数设置为5 000 次，分别经历200 次独立实验，减少随机误差对实验结果的影响。

3.3 测试环境

本实验的测试环境为：硬件运行环境为CPUi7-9750H，内为16 GB，显卡RTX2060，软件运行环境为Windows10系统，运行软件Matlab2019b。

3.4 实验结果分析

经过8 个测试函数的检验，实验结果如表3 和表4所示。

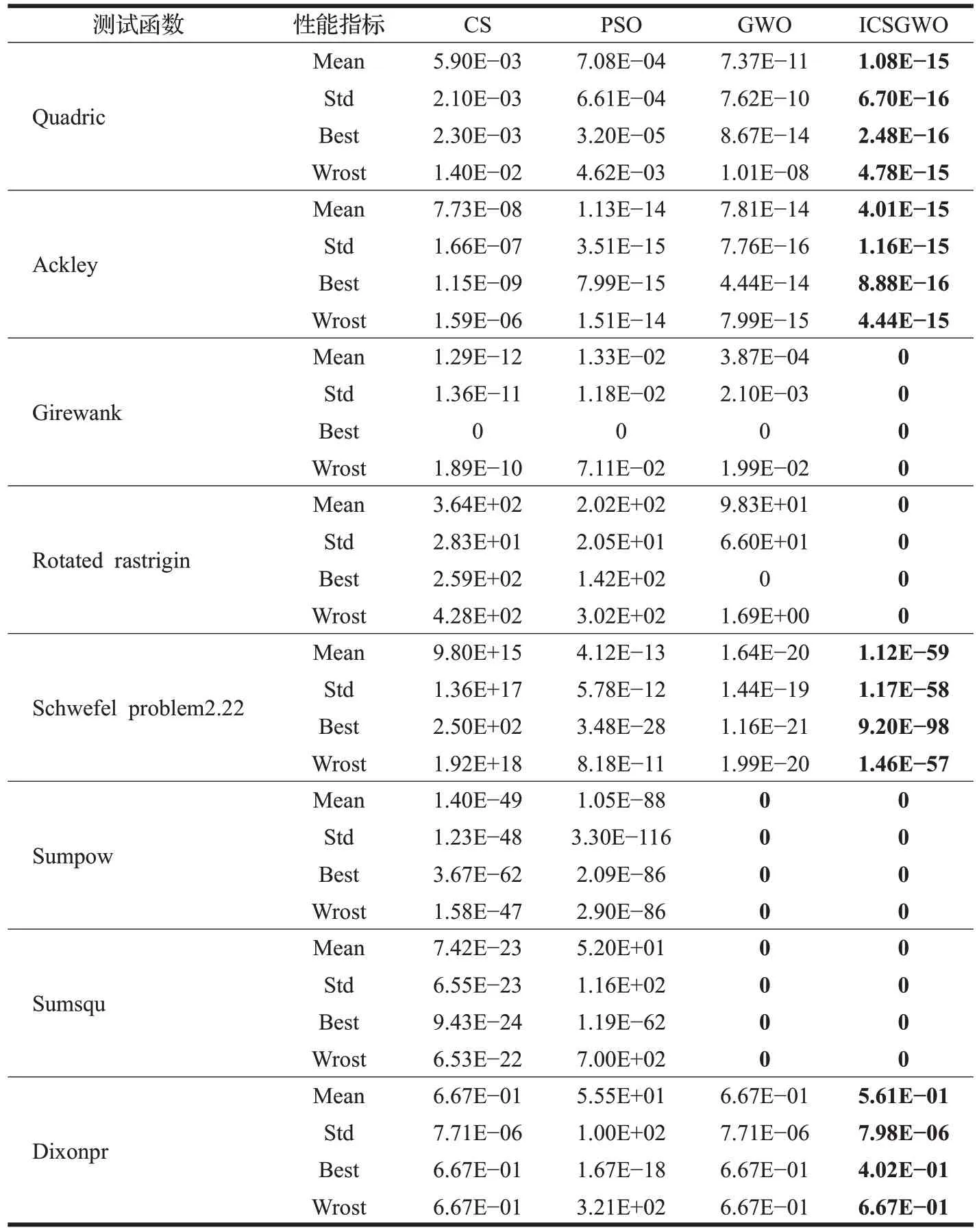
表3 各个算法对应不同测试函数上的优化结果比较Table 3 Comparison of optimization results on different test functions

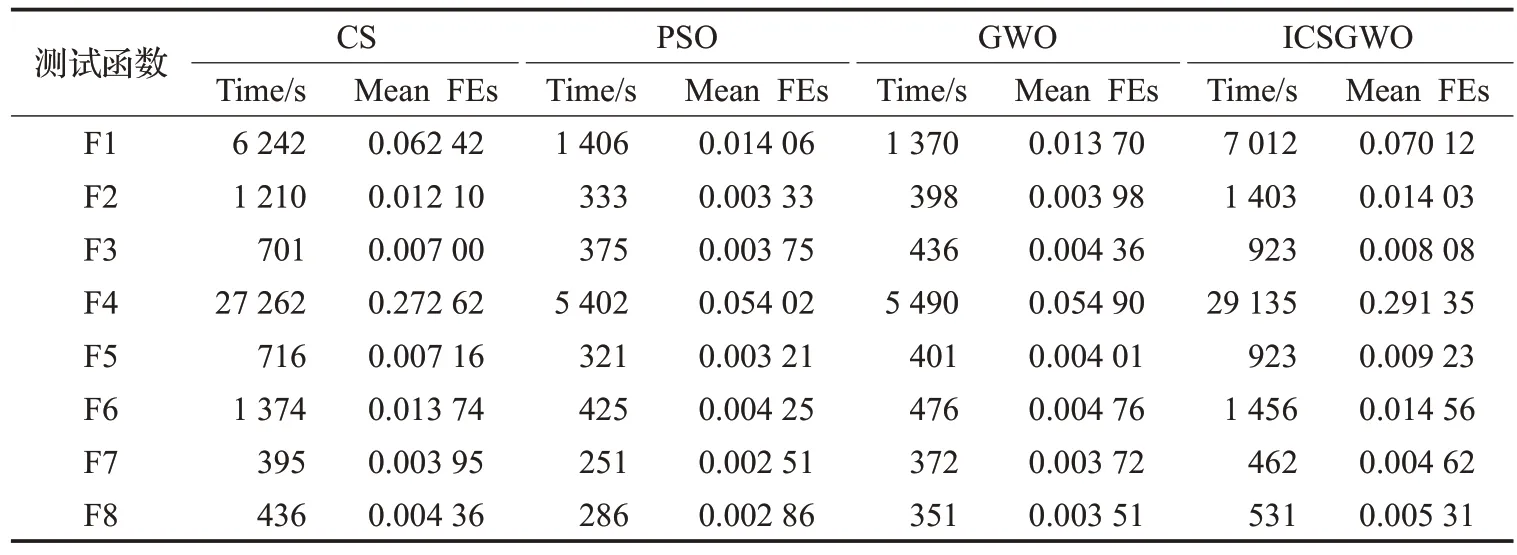
表4 各个算法运行速度比较Table 4 Comparison on running speed of each algorithm

表3通过统计算法最终适应度的平均值（Mean）、标准差（Std）、最优适应度（Best）、最劣适应度（Wrost）来对比各个算法的性能优劣，其中加粗部分代表各算法比较后平均性能最优的性能，表4 通过对算法运行100 000次的总运行的时间（Time）和每次寻优的平均时间（Mean FEs）代表各个算法的运行速度。

由表3可以发现，布谷鸟算法、粒子群算法、灰狼算法在8种测试函数的检验下，有部分测试函数寻优结构并不理想，其中粒子群算法因为其参数少，收敛快的优势被广泛应用于各个领域，但是由于其收敛方式单一，跳出局部最优能力弱，会导致在复杂函数的寻优问题上极易陷于局部极小值，在实验结果上表现为在Quadric函数、Girewank函数、Sumsqu函数、Dixonpr函数上均明显弱于其他三种算法，特别在Sumsqu函数和Dixonpr函数在寻优结果上，其最优适应度表现较好，但是适应度的平均值却并不理想，这是由于粒子群算法在寻优过程中陷入局部最优值，且在较大迭代次数的条件下仍然无法跳出，导致出现坏解影响总体的寻优结果。

布谷鸟算法作为2009 年较新提出的算法，在粒子飞行方式上采用更为随机的莱维飞行模式，有更大的几率跳出函数局部极小值，在全局范围内搜索最优解，在4种测试函数上表现出的性能要略优于粒子群算法，且在其他函数的寻优表现上也较为平均，在对同一函数的多次寻优结果统计中可以看出，布谷鸟算法稳定性较粒子群算法更好，但是在最优值附近收敛精度较差，表现在最优适应度（Best）的总体要劣于粒子群算法，另外布谷鸟算法在Schwefel problem 2.22 函数在寻优上结果非常不理想，这是由于当自变量趋近无穷大时，该函数会形成大量局部极值区域，且选取的维度较高，寻优难度大引起寻优效果的不理想。

灰狼算法作为2014 年提出的一个新兴群智能算法，在5种测试函数的寻优结果上要优于布谷鸟算法和粒子群算法，且均有概率直接找到最优解，表现出良好的全局搜索能力和局部开发能力，但是在Ackley、Rotated rastrigin等测试函数的寻优表现中仍然可以看出有较大的进步空间。

由表4可以发现，在算法的运行效率上，GWO算法与PSO算法各有优劣，但相较于CS算法都更加快速，但CS 算法由于其贪婪策略的存在，需要反复比较计算适应度函数，牺牲了部分的运行时间换来更好的全局搜索能力和进化能力。本文算法在经过改进后，融合的各个算法的优势，并简化了部分流程，虽然复杂性相对三种算法较高，但容易更快收敛到最优值。

综上所述，本文提出的改进布谷鸟灰狼混合算法（improved cuckoo search grey wolf，ICSGWO）在8 种测试函数的寻优结果均要优于其他三种算法，其中在Girewank 函数、Rotated rastrigin 函数、Sumpow 函数、Sumsqu 函数上可以直接收敛到最优解，且表现出优异的稳定性，在其他四种测试函数上也略优于布谷鸟算法、粒子群算法和灰狼算法。

4 结束语

本文通过研究和分析布谷鸟算法和灰狼算法的优势和弊端，针对布谷鸟算法局部搜索能力弱的缺陷，引入粒子群算法的社会学习算子和自我学习算子，并结合灰狼算法的领袖狼机制，提出了一种改进混合布谷鸟灰狼算法。通过比较实验发现，改进算法在保证算法收敛速度和搜索广度的基础上，提高后期的搜索精度，满足算法的收敛性，在各个性能指标上均优于布谷鸟算法、粒子群算法和灰狼算法。