知识图谱嵌入研究综述

徐有为，张宏军，程 恺，廖湘琳，张紫萱，李 雷

陆军工程大学 指挥控制工程学院，南京210007

知识表示与推理是受人类解决问题的启发，将知识符号化，为智能系统获取解决复杂任务的能力而进行的过程和方法，知识图谱技术是知识表示与推理的重要研究内容。知识图谱（knowledge graph，KG）是以图的形式表现客观世界中的实体（概念、人、事物）及其之间关系的知识库，通常表示为三元组(h,r,t)的集合，其中h、t表示实体，r表示实体之间的关系，每个三元组(h,r,t)代表一条事实，即“头实体”h和“尾实体”t之间存在有向关系r。图1 给出了知识图谱的一个典型示例。从图中可以观测到，头实体“The Forbidden City”与尾实体“Beijing”之间存在关系“isLocatedin”，代表“紫禁城位于北京”这个事实成立。知识图谱采取结构化的事实表示方式，具有易组织、易管理、易理解等方面的优势，已吸引了大量来自学业界和工业界的关注性研究。

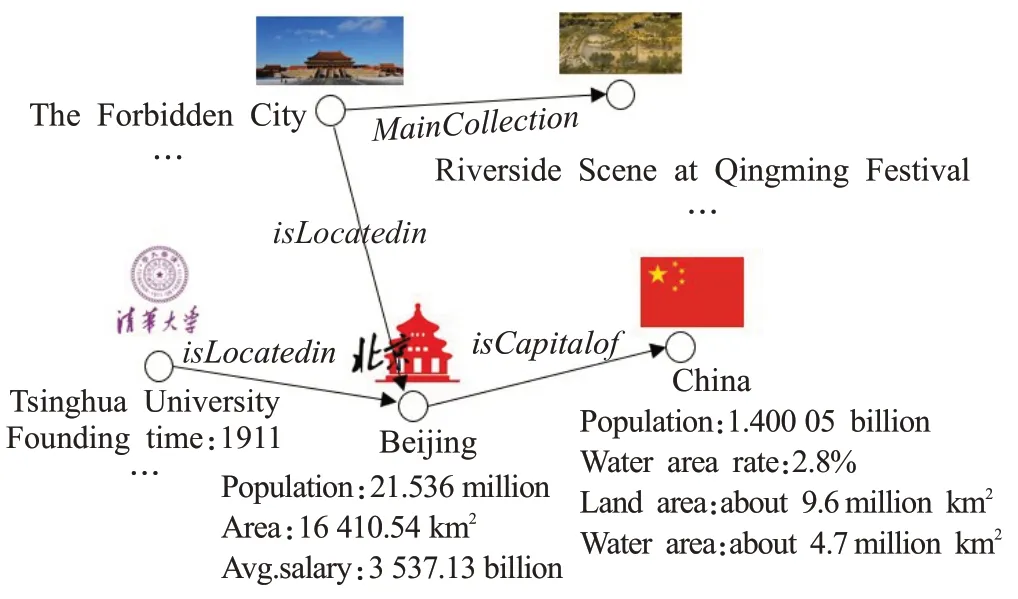
图1 知识图谱示例Fig.1 Example of knowledge graph

知识图谱的研究起源于语义Web。谷歌公司于2012年正式提出知识图谱的概念，并成功应用于搜索引擎，由此推动知识图谱技术成为人工智能领域的重要研究内容。目前，已经涌现出一大批知识图谱，其中具有代表性的有Freebase[1]、WordNet[2]、YAGO[3-5]、DBpedia[6]、NELL[7-8]、KnowItAll[9]、Probase[10]、CN-Probase、XLore等，这些知识图谱从大量数据资源中抽取、组织和管理知识，希望为用户提供能够读懂用户需求的智能服务，例如理解搜索的语义，提供更精准的搜索答案。图2绘制了自2012 年以来知识图谱相关研究论文的检索数量，从图中可以看出，知识图谱的研究成果数量正在成指数方式递增，知识图谱的相关研究正处于飞速发展的阶段（受新冠疫情影响导致大量学术会议被搁置，因此2020年的论文数量没有纳入统计中）。

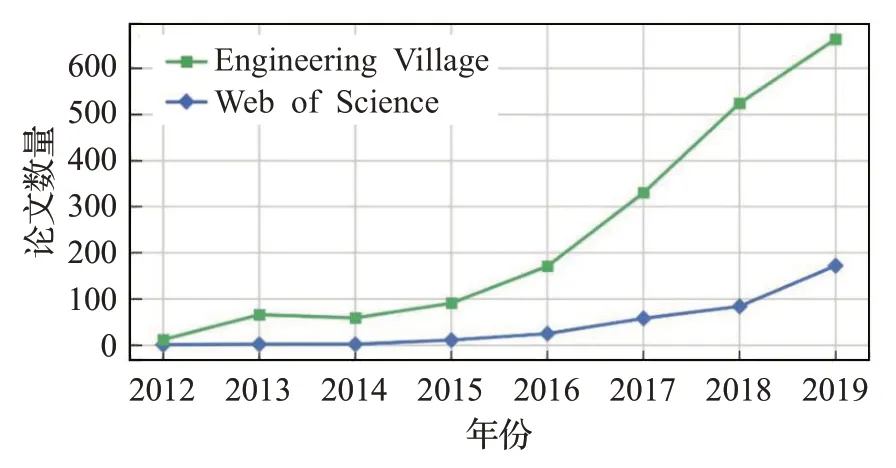
图2 知识图谱论文检索新增数量逐年变化情况Fig.2 Annual changes in number of new papers retrieved on knowledge graph

在知识图谱相关研究中，知识表示是知识应用与获取的基础，是贯穿知识图谱的构建与应用全过程的关键[11]，也是知识图谱相关研究的热点内容。基于知识图谱的知识表示学习（knowledge representation learning，KRL），也称知识图谱嵌入（knowledge graph embedding，KGE），是对知识图谱中的实体和关系完成分布式表示的过程，通过将实体和关系映射到低维向量空间来间接捕获它们的语义。相较于传统one-hot 编码，知识图谱嵌入在显著提升计算效率的同时，能够缓解数据稀疏问题，达到融合异构信息的目的，在知识推理以及整合多源知识方面就显得尤为重要，为下游智能问答、信息检索、系统推荐等任务发挥了必不可少的枢纽作用。表1总结了知识图谱嵌入技术的典型应用案例。

表1 知识图谱嵌入典型应用总结Table 1 Summary of typical applications of knowledge graph embedding

根据面向的知识图谱数量，可将知识图谱嵌入模型划分为面向单个知识图谱的嵌入模型和面向多个知识图谱的嵌入模型。一方面，由于单个知识图谱存在不完整性问题，因此面向单个知识图谱的嵌入模型通常以链接预测（link prediction，LP）作为评测知识图谱嵌入模型性能优劣的关键任务；另一方面，由于不同知识图谱之间存在异构性问题，因此面向多个知识图谱的嵌入模型通常以实体对齐（entity alignment，EA）作为评测知识图谱嵌入模型性能优劣的关键任务。

社会各界对知识图谱的广泛关注，使得知识图谱研究取得了很大的进展，有不少关于知识图谱的综述性文献陆续发表。譬如，文献[27-28]对知识图谱的构建技术进行了综述，文献[29-30]分别针对知识图谱数据管理和可视化进行了综述；文献[11，31-38]综述了知识图谱嵌入、知识表示学习、基于知识图谱的知识推理等内容，为本文知识图谱嵌入模型的分类提供了很多参考依据，但所述均是针对单知识图谱的链接预测模型；文献[39]综述了知识库上的实体对齐技术，但所述均是利用文本相似度进行匹配的算法，没有列举基于知识图谱嵌入的实体对齐方法；文献[40]重点从知识图谱构建、知识表示学习和知识图谱应用三个方面全方位论述了知识图谱技术的整体架构，但是由于所述面相对较宽，导致综述不够聚焦，对知识图谱嵌入这一方面总结不够充分。

当下，知识图谱嵌入领域已经累积了大量的研究成果，为了对现有相关文献有一个系统、深入地梳理与总结，本文围绕知识图谱嵌入模型，主要完成了以下工作：

（1）提出了以面向的知识图谱数量为依据的分类体系：根据面向的知识图谱数量，将现有知识图谱嵌入模型划分成面向单个知识图谱的链接预测模型和面向多个知识图谱的实体对齐模型两大类，其中面向单个知识图谱的链接预测模型进一步划分为距离模型、翻译模型、语义匹配模型、神经网络模型和几何模型五类，面向多个知识图谱的实体对齐模型进一步划分为基于三元组的模型、基于路径的模型和基于图的模型三类。图3绘制了本文的分类体系，并按照时间轴展示了知识图谱嵌入模型的发展变化。

图3 知识图谱嵌入模型分类Fig.3 Schematic diagram of knowledge graph embedding model classification

（2）梳理了近年来链接预测模型的研究进展：面向单个知识图谱的链接预测模型综述已经不少，本文在整合前人的分类体系基础之上，补充增加了近几年的最新研究进展，目的是给出一份较为完整详细的相关研究清单，并围绕最近的研究热点和研究趋势，对其中具有代表性的模型进行介绍。

（3）归纳了实体对齐模型的研究成果：面向多个知识图谱的实体对齐研究是一个新兴的课题，目前尚没有文献综述这些方法，仍然缺乏对实体对齐模型系统、深入的总结工作。为了补充相关领域的空白，本文归纳分析了26 种实体对齐模型，并从不同的方面对它们的核心技术和特征进行了对比。

（4）展望了知识图谱嵌入模型的未来研究方向：基于归纳梳理结果，对未来工作的几个有前途的研究方向进行了全面的展望。

1 问题描述

知识图谱采用多关系有向图的结构化知识表示形式，实体和关系分别被视为多关系图的节点和不同类型的边。具体来说，一般将知识图谱表示为G={E,R,T}，其中E表示实体集合，R表示关系集合，R中的边连接两个实体形成三元组(h,r,t)∈T，代表头实体h与尾实体t之间存在有向关系r，T⊆E×R×E表示知识图谱G中的三元组集合。知识图谱嵌入、链接预测和实体对齐的定义如下。

定义1 知识图谱嵌入（KGE）也称知识表示学习（KRL），是在编码模型C(·)的作用下，为知识图谱中的每个实体e∈E在低维向量空间中完成语义信息表示的过程，即C(e)=e，其中C(·)表示映射函数，e表示实体e的嵌入向量，关系一般被表示为向量空间的运算。知识表示学习得到的分布式表示可以高效地计算实体及实体之间的复杂语义关联。

定义2 链接预测（link prediction，LP）也称知识图谱补全（knowledge graph completion，KGC），是根据知识图谱中已有的知识，生成新知识的过程。即，给定知识图谱G={E,R,T}，链接预测任务通过任给三元组(h,r,t)中的其中两元，预测最有可能的第三元，最终生成不在知识图谱G中的三元组集合G′={(h,r,t)|h∈E,r∈R,t∈E,(h,r,t)∉T}。链接预测根据任务的不同，可分为头实体预测、关系预测和尾实体预测。

定义3 实体对齐（entity alignment，EA）是判断不同知识图谱中的多个实体是否指向真实世界同一对象的过程。不失一般性，考虑两个KG之间的实体对齐任务，即G1={E1,R1,T1}和G2={E2,R2,T2}，给定一组先验对齐的实体对A+={(ei,ej)|ei≡ej,ei∈E1,ej∈E2}⊆E1×E2其中≡表示“对齐”关系，实体对齐的任务是找到新的对齐实体对集合A′，其中A′满足A′={(ei,ej)|ei≡ej,ei∈E1,ej∈E2,(ei,ej)∉A+}⊆E1×E2。

为了统一，本文使用加粗小写字母x表示向量，用‖x‖p表示向量x的p 范数，加粗的大写字母X表示矩阵，表示三维张量。接下来将从面向单个知识图谱的链接预测模型和面向多个知识图谱的实体对齐模型两方面，分析知识图谱嵌入领域的研究现状。

2 面向单个知识图谱的链接预测模型

面向单个知识图谱的链接预测模型的典型学习过程包含三个步骤：（1）首先定义知识图谱G中实体e∈E和关系r∈R在连续向量空间中的表示形式，一般将实体表示为向量空间的确定点，将关系表示为向量空间中的运算，不妨设h和t分别表示头实体h与尾实体t的嵌入向量，通常由随机初始化获得；（2）其次定义三元组(h,r,t)的评分函数fr(h,t)，并根据嵌入向量h和t来评估任意一个事实(h,r,t)成立的可能性，一般得分越高表明事实成立的可能性越大；（3）最后通过优化算法来迭代更新实体和关系的表示。在迭代更新过程中，通常会随机替换真实事实（也称正样例）的头实体或者尾实体来产生一系列的无效事实（也称负样例）。优化过程旨在最大限定提升真实事实的可能性，同时降低无效事实的可能性。

根据模型假设和评分函数的不同，面向单个知识图谱的链接预测模型可以分为距离模型、语义匹配模型、翻译模型、神经网络模型和几何模型五类。

2.1 距离模型

距离模型是最早期的知识图谱嵌入模型，主要是受词向量工具word2vec[41]的启发，将事实的合理性解释为两个实体之间的距离。

Bordes等人[42]遵循词嵌入的研究成果，直接使用头实体和尾实体嵌入向量之间的距离来衡量知识图谱中事实(h,r,t)成立的可能性，提出了知识图谱嵌入的早期模型——UM（unstructured model）模型。UM 模型简单直观，但是无法区分不同的关系类型，只适用于学习仅包含单一关系类型或仅包含等价关系类型的知识图谱嵌入情景。SE（structured embedding）模型[43]通过将每个关系r∈R建模为两个映射矩阵，并分别用于投影事实三元组(h,r,t)中的头实体和尾实体，来改进UM 模型。事实(h,r,t)成立的可能性由投影后的头、尾实体嵌入向量之间的距离来衡量。

但是总体而言距离模型由于假设过于简单，导致其链接预测性能较差，已经很少被提及。

2.2 翻译模型

翻译模型本质上也属于距离模型，同样是利用基于距离的评分函数来衡量事实成立的可能性。相较于距离模型，翻译模型最大不同点是将关系建模为头实体到尾实体的翻译向量。

（1）TransE

TransE[44]是最具代表性的翻译模型，它将实体和关系表示为同一空间中的向量。如图4（a）所示。给定一个事实(h,r,t)，TransE 将关系r解释为翻译向量r，以便嵌入实体向量h和t可以通过r以低误差连接，即当(h,r,t)成立时，h+r≈t。评分函数定义为h+r与t之间的距离：

尽管TransE 具有简单有效的优势，但在处理一对多、多对一、多对多关系时存在缺陷。以一对多关系为例，若(h1,r1,t1)和(h1,r1,t2)同时成立，按照TransE 的模型假设，实体t1和实体t2对应的嵌入向量需要满足t1≈t2的关系，这会导致模型对实体的区分能力降低。

（2）TransH

TransH[45]模型是TransE 模型的扩展。为了解决TransE在处理一对多、多对一和多对多关系类型时存在的缺陷，TransH 采取的改进措施是：允许实体在涉及不同关系时具有不同的表示形式。具体来说，TransH将每个关系r建模为一个超平面上的法向量wr和一个位于该超平面的关系向量r，在为事实三元组(h,r,t)进行打分前，需要首先将头、尾实体的嵌入向量投影到关系r所在的超平面，即：

基于TransE 的假设，TransH 模型认为投影后的实体h⊥和t⊥可以通过r以低误差连接，如图4（b）所示。

（3）ManifoldE

ManifoldE[46]模型代表了TransE 模型的另外一种扩展方向，同样为了解决TransE 在处理一对多、多对一和多对多关系类型时存在的缺陷，ManifoldE 采取的改进措施是：放宽h+r≈t的过度约束要求。具体来说，ManifoldE为每个关系r额外定义了一个超球体的半径θr。对于每一个事实三元组(h,r,t)，ManifoldE 模型认为尾实体t对应的嵌入向量t位于一个以h+r为中心，以θr为半径的超球面上，而不是位于h+r的精确点上，如图4（c）所示。

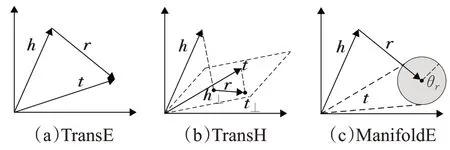
图4 翻译模型示意图Fig.4 Schematic diagram of translational models

（4）其他翻译模型

除了上述3种翻译模型以外，KG2E[47]将实体和关系表示为从多变量高斯分布中提取的随机向量来模拟实体和关系中的不确定性；TransR[48]将关系建模为实体空间到关系空间的投影矩阵；TransD[49]在TransR基础上将投影矩阵进一步分解为两个向量的乘积；TranSparse[50]通过在投影矩阵上实施稀疏性来简化TransR；TransM[51]为每个关系定义权重且为一对多、多对一、多对多关系类型分配较低权重值；TransF[52]仅要求t与h+r、h与t-r处于同一方向；TransA[53]通过为每个关系r引入对称的非负矩阵Mr实现自适应度量；TransG[54]认为关系可以具有多种语义并将其表示为高斯分布的混合体；STransE[55]是SE 和TransE 模型的简单组合；ITransF[56]借助稀疏注意力机制获得了发现隐藏共享概念的能力；TransAt[57]同时学习基于翻译的嵌入和实体的关系相关类型，并利用实体属性的层次结构提出了两阶段判别法的注意力机制。

2.3 语义匹配模型

语义匹配模型利用基于相似性的评分函数，通过匹配实体的潜在语义和向量空间表示中体现的关系来衡量事实的合理性。与上述两类模型相比，语义匹配模型通常采用乘法算子构建实体和关系嵌入向量之间的交互关系，因此有学者也将距离模型和翻译模型统称为加法模型，将语义匹配模型称为乘法模型。

（1）RESCAL

RESCAL[58]模型也称双线性模型，是最早的语义匹配模型，其表示学习过程一般通过张量分解完成。RESCAL将关系r建模为矩阵Mr，以捕获实体潜在因子之间的成对相互作用。具体来说，关系矩阵Mr的各个权重捕捉头实体向量h的第i个潜在因子hi和尾实体向量t的第j个潜在因子tj之间的相互作用量。因此给定一个事实(h,r,t)，该事实成立的可能性由公式（3）衡量：

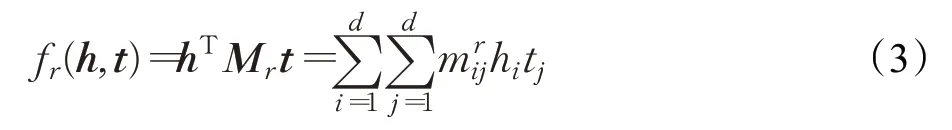
通过评分函数可以看出：RESCAL 需要捕获h和t所有分量之间的成对交互作用。

（2）SimplE

在RESCAL 模型基础之上，SimplE[59]将关系矩阵Mr限制为对角阵，因此关系矩阵可以简化用向量r表示。SimplE强调：实体e在三元组中所扮演的主体角色和客体角色应该有所区分，并为每个实体e编码了两个嵌入向量eh和et，分别对应实体e被用作事实三元组的头实体和尾实体。同时SimplE 模型还假设：当事实三元组(h,r,t)成立时，其反向事实三元组(t,r-1,h)也同时成立，其中r-1表示关系r的逆，因此SimplE 为每个关系r同样编码了两个向量r和r-1，分别对应关系的正方向和逆方向。为了充分考虑同一实体两个向量之间的关联，评分函数定义为正向事实(h,r,t)及其反向事实(t,r-1,h)得分的平均值，即：

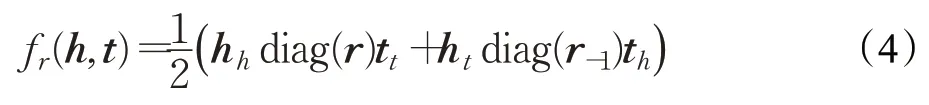
已经证明SimplE 是完全表达的，即给定任何有效的知识图谱，在该模型的假设下至少存在一种嵌入方案，能够将所有真实事实三元组与无效事实三元组分开。换句话说：SimplE模型在理论上有潜力正确学习任何有效的知识图谱，而不受内在限制的阻碍。

（3）TuckER

TuckER 模型[60]将知识图谱表示为三阶二元张量，并引入了三阶张量的TuckER 分解方法，通过输出核心张量、实体及关系的向量来学习嵌入，其评分函数定义为：

其中，×k表示张量积，k表示张量积的运算维度。核心张量可以看做原始关系矩阵的共享池，隐含了实体和关系向量之间的交互程度。TuckER同样是完全表达的，并且RESCAL和SimplE均可解释为TuckER模型的特殊情况。此外，TuckER模型中实体嵌入和关系嵌入的维度相互独立，可以根据实体规模和关系规模分别设置。

（4）CrossE

CrossE[61]模型认为实体和关系之间的双向效应有助于在链接预测时选择相关信息，因此CrossE除了为每个实体和关系学习通用嵌入以外，还为每个关系r学习附加嵌入cr来模拟实体和关系之间的双向交互。对于给定事实三元组(h,r,t)，CrossE定义头实体和关系的交互嵌入如下：

其中，⊙表示Hadamard 乘积。受益于交互嵌入的CrossE 更有能力生成可靠的解释来支持链接预测任务。需要说明的是，CrossE模型相对通常意义上的语义匹配模型而言具有一定的特殊性，一方面CrossE借鉴了翻译模型的假设，让头实体的交互嵌入向量和关系的交互嵌入向量通过翻译特性的加法算子连接；另一方面，CrossE也具有神经网络模型的特征，在运算中插入了非线性激活函数。

（5）其他语义匹配模型

除了上述4 种语义匹配模型以外，SME[62]提出在语义上匹配实体关系对(h,r)和(r,t)的单独组合；LFM[63]在RESCAL 模型基础上将关系矩阵分解为潜在关系因子的稀疏表示；TATEC[64]不仅学习RESCAL的三向交互，还建模了两向交互作用；TRESCAL[65]使用关系领域知识来捕获潜在有效的事实三元组，显著降低了RESCAL的时间复杂度和空间复杂度；DistMult[66]将关系矩阵Mr限制为对角矩阵来简化RESCAL；HolE[67]引入了嵌入的循环相关性来学习组合表示；ComplEx[68]通过引入复数嵌入扩展了DistMult，以便更好地对非对称关系建模；ANALOGY[69]通过限制关系矩阵Mr正交且满足交换律来扩展RESCAL，以进一步建模实体和关系的类比属性；HolEx[70]借助插值运算，可视为HolE 多个线性扰动副本的连接。

2.4 神经网络模型

神经网络具有强大的特征捕获能力，它可以通过非线性变换将输入数据的特征分布从原始空间转换到另一个特征空间，并自动学习特征表示。知识图谱嵌入模型中的神经网络模型，就是借助神经网络的强大学习能力，来完成实体和关系的特征表示。

（1）NTN

NTN模型[71]认为翻译模型存在参数不交互的问题，并借鉴了语义匹配模型的张量表示，使用双线性张量层代替标准线性神经网络层，构建了表达性神经张量网络，如图5（a）所示。该双线性张量层直接关联了跨多个维度的实体向量，解决了翻译模型存在的参数交互问题。其评分函数定义为：

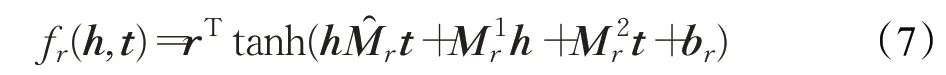
（2）ConvE

ConvE[72]是一种基于CNN 的方法，通过将头实体、关系对(h,r)视为特征图来建模实体和关系之间的相互作用。具体来说，对每个事实三元组(h,r,t)，首先将头实体向量h和关系向量r重塑为2D矩阵Mh和Mr，并将拼接后的矩阵[Mh;Mr]输入带滤波器ω的2D 卷积层；其次将卷积层的输出张量重塑为向量，并输入参数矩阵为W的全连接层，其中c表示维度为m×n的2D特征图数量；最后将全连接层的输出向量与尾实体向量t进行内积运算，得到的数值即为ConvE 模型为事实三元组(h,r,t)的评分。图5（b）绘制了ConvE 模型的运算过程。ConvE 通过多层非线性特征学习来表达语义信息，由卷积生成的特征映射增加了潜在特征的学习能力。ConvE还可以通过1～N评分提升运算速度，具有很高的参数效率，在建模具有高关联度的实体时特别有效。

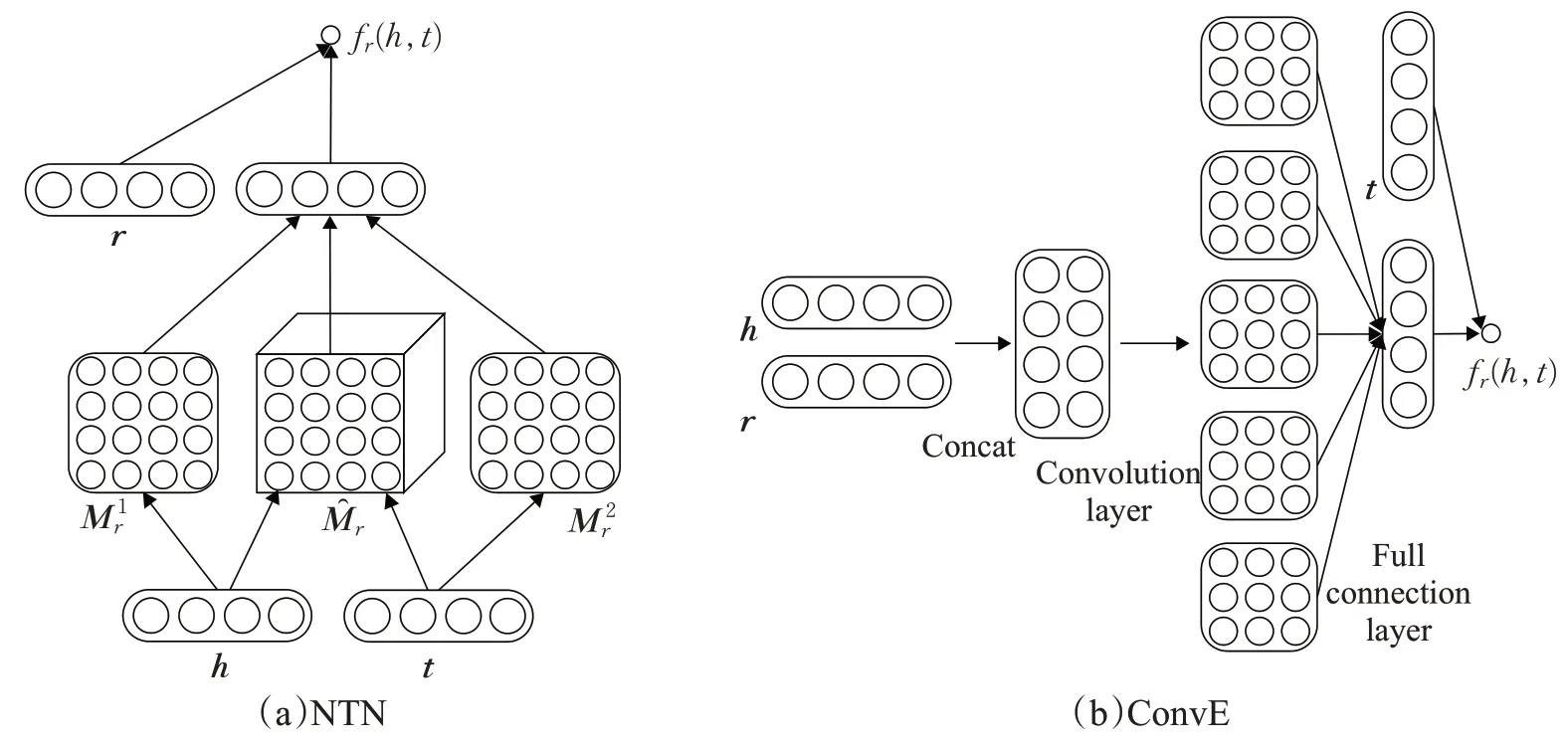
图5 神经网络模型示意图Fig.5 Schematic diagram of neural network models

（3）CapsE

CapsE[73]模型假设不同嵌入向量在相同位置编码同源信息，并使用胶囊神经网络来学习实体和关系表示。不同于ConvE在前向运算时只关注(h,r)对，CapsE在输入层整合事实三元组(h,r,t)的编码，通过拼接头实体、关系和尾实体的向量h、r、t得到矩阵[h;r;t]；并且CapsE 没有重塑操作，矩阵[h;r;t]将直接输入滤波器大小固定为1×3 的卷积层来获取特征信息。在胶囊层中，每个胶囊节点只处理相同位置的特征编码，故单独的胶囊节点只接收输入事实某一个方面的信息。最终产生的向量长度即为事实三元组(h,r,t)的评分。

（4）其他神经网络模型

除了上述3 种神经网络模型以外，SLM[71]采用标准单层神经网络来隐式连接实体向量；MLP[74]将事实三元组(h,r,t)在输入层拼接成一个向量后送入全连接层，最后在线性输出层得到该三元组的分数，SLM 和MLP均可视为NTN的特例；NAM[75]将(h,r)对的隐藏编码与尾实体向量t进行匹配，提出了关系调制神经网络；ProjE[76]区分输入信息和候选实体集，提出使用共享变量神经网络模型，实现了较小的参数空间；与CapsE一致，ConvKB[77]将三元组作为三列的矩阵输入，并采用一维卷积模拟实体关系之间的交互，模型可视为面向事实(h,r,t)的二分类器；R-GCN[78]针对知识图谱的高度多关系数据特性，采用关系图卷积网络来学习实体表示；SACN[79]由编码器加权图卷积网络和解码器Conv-TransE组成，前者获得图的结构信息，后者使模型可以完成链接预测任务；ConvR[80]在ConvE 基础之上提出使用带特定关系滤波器的自适应卷积；HypER[81]对超图网络进行关系特定的一维卷积滤波，实现多任务知识共享。

2.5 几何模型

几何模型将关系解释为语义空间中的几何变换，将经过空间几何变换后的头实体向量与尾实体向量t之间的距离作为事实三元组(h,r,t)的得分。严格从定义上来说，距离模型和翻译模型也属于几何模型的范畴，本文为了与距离模型、翻译模型进行区分，将几何模型中涉及的几何变换定义为除了平移变换以外的复杂变换。

（1）RotatE

RotatE[82]把实体和关系建模到复数空间，并将关系描述为复数域空间的旋转变换，如图6（a）所示。当事实三元组(h,r,t)成立时，RotatE 模型假定h⊙r=t，其中，并且关系向量每一维的模长被限制为1，即|ri|=1，其评分函数定义为：

已经证明，RotatE 可以正确地模拟许多关系模式，如对称/反对称、反转和合成等。此外，RotatE还提出了一种新的自对抗负采样策略来高效地训练模型。

（2）QuatE

QuatE[83]指出：复数域的Hadamard 乘积具有交换律，导致RotatE 在建模合成关系模式时存在缺陷。不妨假设存在两个关系r1和r2分别表示“isFatherof”和“isSpouseof”，由于RotatE 假定r1⊙r2=r2⊙r1，因此隐含的认为“父亲的配偶”和“配偶的父亲”表示的是同一个关系，然而这并不符合现实场景的应用需求。因此QuatE 引入了超复数表示来建模实体和关系。具体来说，QuatE 采用具有三个虚分量的四元数嵌入，关系被建模为四元数空间中的旋转，因此头实体向量h可以表示为h=ah+bhi+chj+dhk，ah,bh,ch,dh∈ℝd，h∈Hd，其中Hd表示d维四元数空间，关系向量r表示为r=ar+bri+crj+drk，ar,br,cr,dr∈ℝd，r∈Hd。QuatE定义评分函数如下：

其中，⊗表示Hamilton乘积，用来捕捉实体和关系的四维空间中潜在的相互依赖，r⊲表示关系r的归一化结果，即限制关系每一维的模长为1。与只有一个旋转平面（即复数域平面）的RotatE相比，QuatE有两个旋转平面，解决了RotatE 在上述合成关系模式中存在的缺陷，表达的语义更加丰富。

（3）MuRP

MuRP[84]注意到实体之间关系的层次性特点，提出在双曲空间中对实体建模。MuRP 首先将实体向量定义在半径为的d维庞加莱球模型中，即h,t∈；接下来使用Möbius矩阵-向量乘法将原始头实体向量h转换为关系适应的头实体向量，使用Möbius 加法将原始尾实体向量t转换为关系适应的尾实体向量t(r)=t⊕cr，其中，R∈ℝd×d表示欧式空间的对角关系矩阵，表示双曲空间的关系平移向量，表示在两个空间进行转换的映射矩阵，借助庞加莱球模型中的距离度量dB，MuRP 定义评分函数如下：

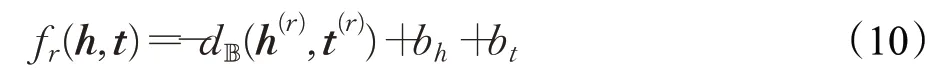
bh和bt表示头尾实体的偏置，用于衡量超球面判定边界的半径，如图6（b）所示，距离在的尾实体均被视为正确的事实；最后MuRP用黎曼方法完成迭代优化。由于庞加莱圆盘的性质-离中心越远，单位欧几里德空间的线段所代表的长度越长-因此能够建模实体间的层次性关系。

（4）HAKE

HAKE[85]同样从研究实体之间语义层次的角度出发，考虑在极坐标系中表示实体和关系。结构上HAKE模型由模数部分和相位部分组成，以头实体为例，hm和hp分别表示头实体向量h=(hm,hp)，hm,hp∈ℝd的模数向量和相位向量。模数部分旨在对层次结构中不同层级的实体进行建模，层级越高的实体模值越小，关系rm被建模为不同层级之间的尺度变换；相位部分旨在区分同一层级的不同实体，关系rp被建模为实体之间的旋转变换，如图6（c）所示。HAKE取模数部分分值和相位部分分值的加权和评估事实三元组(h,r,t)成立的可能性。相较于RotatE，HAKE 显示的建模模值大小，借助极坐标系中的同心圆来感知层级关系，能获取更丰富的语义信息。

图6 几何模型示意图Fig.6 Schematic diagram of geometric models

（5）其他几何模型

除了上述4种几何模型以外，Poincare[86]同样采用庞加莱球完成建模，但是没有考虑关系在事实三元组中的作用，可视为MuRP的简化版；TorusE[87]将实体和关系投影到环面空间中，并借助李群定义环面距离完成事实评分；DihEdral[88]采用二面体群进行旋转，将多个二面体群组成关系对角矩阵，能从理论上解决对称、反对称、翻转、组合等关系类型；ATTH[89]提出双曲注意力机制，在双曲空间下同时学习知识图谱的层次性与逻辑关系。

2.6 小结

链接预测任务的基准数据集一般通过对现实世界中的知识图谱进行抽样获得，并按照模型需求拆分为训练集Ttrain、验证集Tvalid和测试集Ttest。相关统计信息由表2给出。

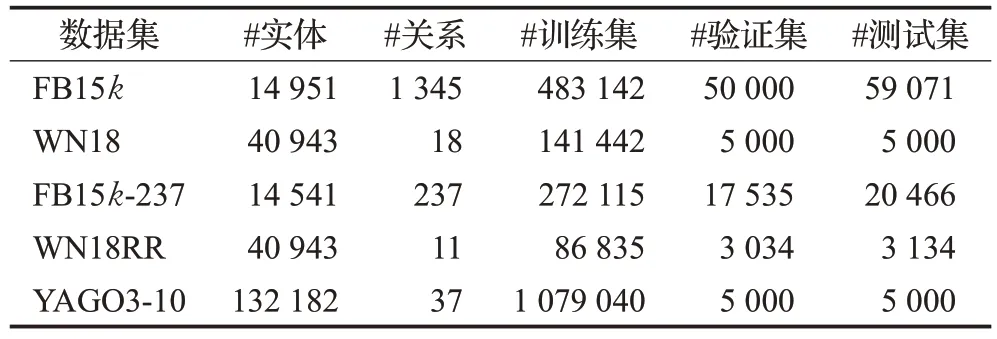
表2 链接预测数据集统计信息Table 2 Statistics of datasets for link prediction task

（1）FB15k：Freebase 是一个大型跨域知识图谱，由大约12亿个三元组和超过8 000万个实体组成。Bordes等人[44]选择了Freebase 中所有被提及100 次以上的实体以及所有与这些实体相关的事实，构建了其子集FB15k。FB15k主要包含了描述电影、演员、奖项、体育和运动队事实的三元组。

（2）WN18：Bordes 等人[44]通过过滤掉Wordnet 中被提及较少的实体和关系，提取了Wordnet的子集WN18，其中Wordnet是一个描述词汇关系的知识图谱，旨在提供自然语言处理和自动文本分析。

（3）FB15k-237：Toutanova 和Chen[90]发现FB15k存在测试泄露问题，即测试集中超过80%的三元组是训练集中包含的三元组的逆序，并在此基础上通过删除逆关系，构造了更具挑战性的FB15k-237数据集。FB15k-237本质上是FB15k的子集。

（4）WN18RR：与FB15k-237 类似，Dettmers 等人[72]发现，WN18 存在与FB15k相同的测试泄露问题，并通过同样的处理方法删除WN18 中的逆关系，构造了WN18RR数据集。WN18RR本质上是WN18的子集。

（5）YAGO3-10：YAGO 是一个大型知识图谱，包含从维基百科中提取并与Wordnet对齐的事实。Dettmers等人[72]通过选择至少有10 种不同关系的实体，构建了YAGO 的子集YAGO3-10，其中大多数三元组描述了人物的公民身份、性别和职业等属性信息。实验表明[72]，YAGO3-10不存在测试泄露问题。

针对测试集Ttest的每一个三元组(h,r,t)，链接预测模型隐藏头实体并计算所有实体在该头实体预测(?,r,t)中的得分，获取真实头实体h的排序rankr,t(h)；并用类似的过程获取真实尾实体t在该尾实体预测(h,r,?)中的排序rankh,r(t)。根据上述单个排序，链接预测模型的整体性能指标通常包括：

（1）平均排序（mean rank，MR），MR 被定义为测试集上所有三元组排序的算数平均值，即：

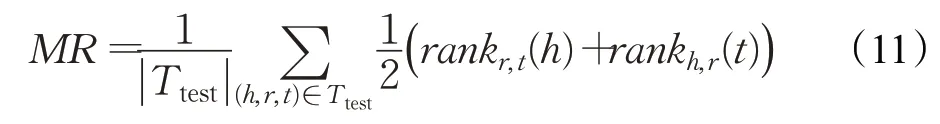
MR数值越小，代表模型的链接预测性能越好。

（2）平均倒数排序（mean reciprocal rank，MRR），MRR被定义为测试集上所有三元组排序倒数的算数平均值，即：

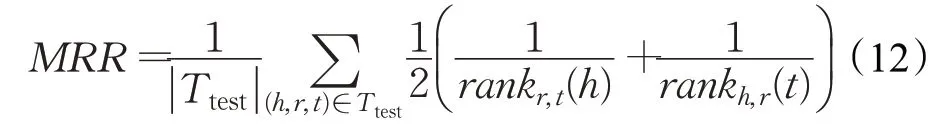
MRR 具有平滑性，且相较于MR，受异常值的影响更小。MRR 的取值范围为MRR∈(0,1]，数值越大，代表模型的链接预测性能越好。

（3）Hits@k，Hits@k表示在测试集中，单个排序位于前k的三元组比率，即：

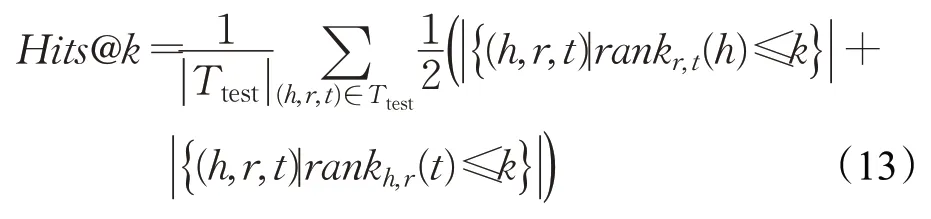
Hits@k数值越大，代表模型的链接预测性能越好。k通常取1，3和10。

表3总结了上述五类链接预测模型的优缺点。

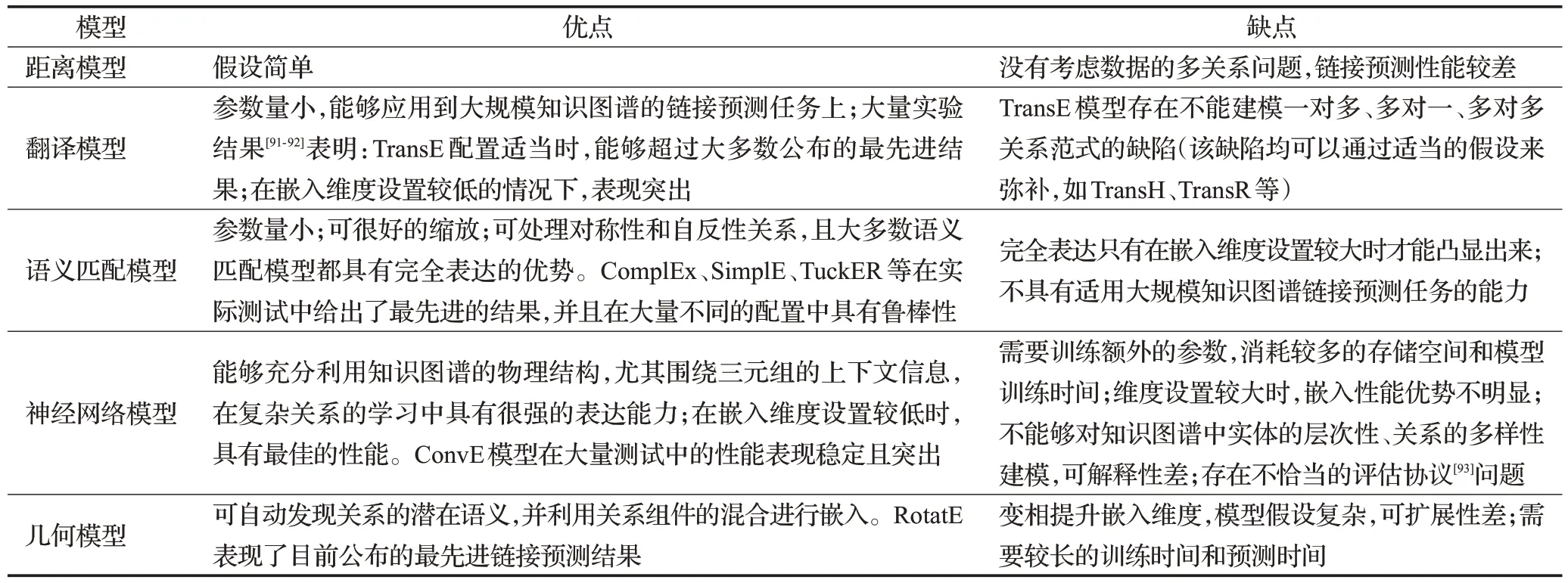
表3 链接预测模型优缺点总结Table 3 Summary of advantages and disadvantages of link prediction models

需要说明的是，受模型结构、模型超参数（例如嵌入维度和负样本数量）和数据集大小影响，即使是相同模型也会表现出较大的性能差异，没有哪个配置在所有数据集上表现最好，也不存在绝对性能优异的模型。实际应用中，需要根据情况在所需内存和性能之间做权衡。

表4 给出了上述所有面向单个知识图谱的链接预测模型的实体表示、关系表示和评分函数。

表4 面向单个知识图谱的链接预测模型总结Table 4 Summary of link prediction models oriented to single knowledge graph

此外，有大量学者认为，单一知识图谱提供的语义信息不足以支撑高性能的链接预测任务，为了促进更有效的知识表示h,t∈ℝd，包含附加信息的知识图谱嵌入模型将附加信息（如文本描述等）与知识图谱本身结合在一起，通过使用额外的辅助信息来补充实体语义，加强结构嵌入，从而提升链接预测性能。这些附加信息主要包括：（1）文本描述：DKRL[94]通过组合结构表示和描述表示来生成实体和关系的嵌入，其中结构表示由TransE学习，描述表示由连续词袋（CBOW）和深度卷积神经网络模型（CNN）生成；KG-BERT[95]将知识图中的三元组视为文本序列，以实体和关系描述为输入，利用BERT进行微调。（2）关系路径：PTransE[96]将关系路径视为实体间的转换，使用关系的组合表示关系路径；RSNs[97]使用有偏随机游走从训练事实中学习关系路径。（3）实体类型：TKRL[98]将实体类型建模为投影矩阵，并将父类的投影矩阵表示为其子类矩阵的组合，投影后的实体通过TransE 学习。（4）实体属性：KR-EAR[99]将实体与属性之间的相关性建模为分类任务，为属性三元组定义了单独的评分函数；MT-KGNN[100]和KBLRN[101]在共享的嵌入空间，同时学习结构表示和属性编码，其中属性编码通过神经网络预测模型实现。（5）逻辑规则：UGKE[102]根据不确定关系事实的置信度得分来学习嵌入，在嵌入空间中同时保留关系事实的结构信息和不确定信息；pLogicNet[103]使用具有一阶逻辑的马尔可夫逻辑网络来定义所有可能三元组的联合分布，实现在知识图谱嵌入中融入领域知识。（6）视觉信息：IKRL[104]使用图像编码器为多值图像关系的每个实例生成嵌入；MKBE[105]使用CNN 对图像三元组的向量进行编码，并采用了DistMult的评分函数。

3 面向多个知识图谱的实体对齐模型

面向多个知识图谱的实体对齐模型同样将知识图谱中的实体映射到低维向量空间，通过向量空间的几何结构捕捉实体的语义相关性，同时隐含的弱化不同知识图谱之间的异构性问题。实体对齐模型一般只考虑两个知识图谱的任务场景，图7描述了实体对齐模型的典型框架。

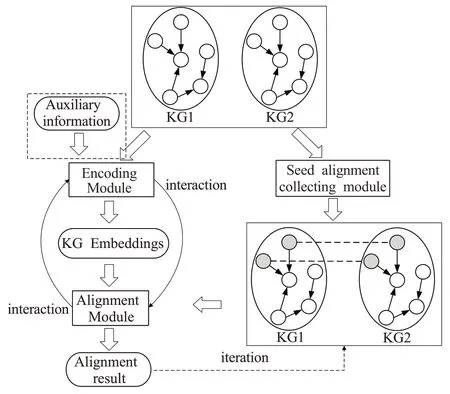
图7 实体对齐模型典型框架Fig.7 Typical framework of entity alignment models

实体对齐模型需要预先收集两个输入知识图谱之间的种子实体对，并与编码模块获得的实体嵌入一起送入对齐模块，用于发现新的实体对齐结果。编码模块与对齐模块的交互方式一般有两种：（1）编码模块在两个独立的语义空间中分别编码两个知识图谱，对齐模块借助种子实体对学习两个语义空间之间的映射投影；（2）对齐模块通过约束种子实体对的向量保持较高相似度，来引导编码模块将两个知识图谱编码到同一个语义空间。此外，为了克服种子实体对不足的问题，有些模型会在学习过程中迭代地增加新的对齐实体，也有模型通过使用额外的辅助信息来补充实体语义，加强结构嵌入，提升实体对齐性能。

按照编码模块捕获语义的层次，面向多个知识图谱的实体对齐模型可以分为基于三元组的模型、基于路径的模型和基于图的模型三类。

3.1 基于三元组的模型

基于三元组的模型只关注实体与实体之间的一跳关系，从三元组的视角对实体和实体之间的关系进行建模，认为不同事实三元组(h,r,t)之间相互独立。这种视角与大多数面向单个知识图谱的链接预测模型一致，因此可以很自然将链接预测模型作为实体对齐的编码模块，基于三元组的模型通常采用TransE完成编码。

（1）MTransE

MTransE[106]是最早提出用嵌入方法解决实体对齐任务的模型。MTransE采用TransE作为编码模块，将每个知识图谱的实体和关系分别编码在相互独立的嵌入空间中，并为种子实体对中实体的嵌入向量提供转换函数，同时保留了单知识图谱嵌入的功能。因此，MTransE定义损失函数为：

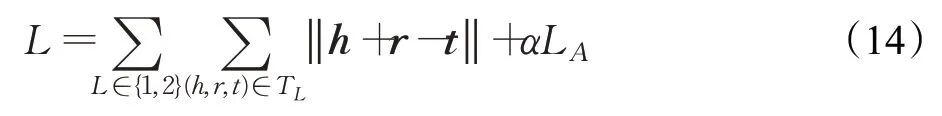
其中，第一项表示编码模块损失，第二项LA表示对齐模块损失，α是超参数，用于衡量两种损失之间的权重。针对对齐模块，MTransE 提供了轴校准、平移向量和线性转换三种策略，通过实验得出，相较于轴校准和平移向量，选取线性转换作为对齐模块，在实体对齐任务上表现最佳。

（2）BootEA

BootEA[107]同样采用TransE作为编码模块，在MTransE模型基础之上，BootEA提供了“参数交换”策略，通过互相交换已对齐实体对(e1,e2):e1∈E1,e2∈E2的实体，扩充有效事实三元组。扩充的三元组包括：

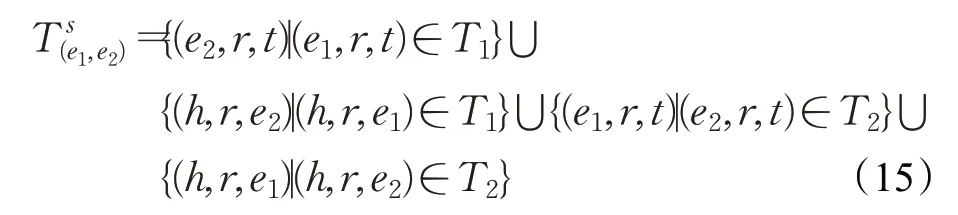
在对齐模块，BootEA 将实体对齐任务描述为一对一分类问题，对齐模块的损失定义为来自不同知识图谱实体分布之间的交叉熵。训练过程中，BootEA 提出了一种实体对齐自举方法，迭代地将可能的实体对齐标记为训练数据用于学习面向对齐的知识图谱嵌入，并采用对齐编辑来减少迭代过程中的误差累积。

（3）OTEA

与上述方法的编码模块一样，OTEA[108]同样选取TransE实现实体嵌入。针对对齐模块，OTEA认为在实体级别定义的对齐损失只能服务于已标记实体而不能匹配整个图像，因此提出从实体级损失和组级损失两个维度进行双重优化，并定义组级损失函数为最佳传输距离下的差值。此外在实体级损失方面，OTEA还强调不同知识图谱之间的对偶性，因此从两个方向同时学习对齐，实体级损失定义为：

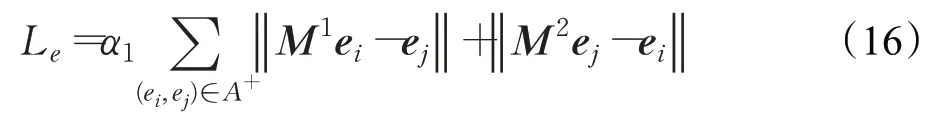
M1和M2分别表示两个方向的转移矩阵。OTEA还对对偶平移矩阵施加正则化以减轻变换过程中噪声的影响。

（4）TransEdge

TransEdge[109]的改进主要针对编码模块，不同于上述方法以实体为中心完成嵌入，TransEdge以边为中心，根据特定的头-尾实体对完成关系表示，这种关系的上下文表示称为边嵌入，并将边嵌入解释为实体嵌入之间的转换。TransEdge编码模块的评分函数为：

其中，ψ(hc,tc,r)表示关系的上下文运算，hc和tc表示头实体和尾实体的交互嵌入。在对齐模块，TransEdge提出了“参数共享”策略，即强制种子实体对齐中的一对对齐实体具有相同嵌入。TransEdge同样采用自举方式迭代的训练数据，但是“参数共享”策略不对自举的实体对施用。

（5）其他基于三元组的模型

除了上述4 种基于三元组的模型以外，JAPE[110]将两个知识图谱的结构联合嵌入到一个统一的向量空间中，并利用KG 中的属性相关性进一步细化实体嵌入；KDCoE[111]在基于翻译的编码模块之上，增加了实体描述编码模块，两种编码模块迭代联合训练；NTAM[112]提出了一种非平移方法，利用概率模型为对齐任务提供更鲁棒的解决方案；AttrE[113]将属性三元组纳入知识图谱嵌入中，使用统一的谓词命名方案为关系嵌入提供一致的向量空间，利用传递性规则丰富实体的属性数目，增强属性嵌入；IMUSE[114]声称是一种无监督的方法，通过交替执行实体对齐和属性对齐产生大量的高质量对齐实体对，用于训练关系嵌入模型，通过二元回归模型来表示实体对的最终相似性；SEA[115]和AKE[116]利用对抗式学习的思想建模实体的向量空间，为了获得映射的自洽性，SEA采用循环一致性限制、AKE新增正交约束来利用未对齐的实体；MultiKE[117]从实体名称、关系和属性三个视角对实体信息进行编码和高效集成；MMEA[118]采用ComplEx 作为编码模型改善了实体对齐性能。

3.2 基于路径的模型

不同于基于三元组的模型只关注知识图谱中的单跳信息，基于路径的模型认为单跳信息难以实现实体之间的语义传播，只能获取实体片面的局部的语义信息，因此着眼于挖掘实体之间的关系路径，并捕获实体之间的长关系依赖，其中关系路径是一组首尾相连的关系三元组。

（1）IPTransE

IPTransE[119]最早尝试从路径的视角解决实体对齐任务，与MTransE 模型类似，IPTransE 同样在相互独立的编码空间分别表示两个知识图谱的实体。不同的是，为了捕获知识图谱中的关系路径，IPTransE 使用PTransE 而不是TransE 作为编码模块，通过推断直接关系和多跳路径之间的等价性来建模关系路径。假设存在事实三元组(h,r1,e1)和(e1,r2,t)，实体h到实体t的关系路径p被编码为其组成关系嵌入的组合，即：

其中，comb(·)是一个序列合成操作。PTransE可以通过考虑实体之间的路径来对间接连接的实体进行建模，这些关系谓词形成了实体之间的转换。针对对齐模块，IPTransE提出了平移向量、线性转换和“参数共享”三种策略，“参数共享”策略在大量实验中表现出最佳的对齐性能。此外，为了增加对齐实体对，并减少自举过程中的错误传播，IPTransE提出包含可靠性分数的软对齐策略，以添加到目标函数的损失项中完成优化。

（2）RSNs

RSNs[97]使用循环跳跃网络来有效捕捉实体的长期关系依赖，在链接预测和实体对齐两个任务中均表现出了优异的性能。具体来说，知识图谱的关系路径通过有偏随机抽样产生，与MTransE只着眼于单个知识图谱内部的关系路径不同，RSNs 还考虑了跨知识图谱的关系路径。此外在抽样过程中，RSNs 为单知识图谱内部路径抽样设置了深度优先策略，为跨知识图谱路径抽样设置了同图搜索偏好，既避免了在同图内循环重复，也避免了在种子实体对之间来回走动。有偏随机游走旨在抽样能够正确描述图形的路径，来确保图的所有特征都被采样。

（3）DAT

DAT[120]提出使用名称编码模块和结构编码模块共同表示实体信息，并采用RSNs[97]作为结构编码模块，采用级联幂平均嵌入方法作为名称编码模块；针对对齐模块，设计了一个度感知协同注意网络，将实体的度作为有效融合两种不同信息源的重要指导，动态调整不同特征的重要性。实体对的相似度定义为结构相似度和名称相似度的注意力加权和：

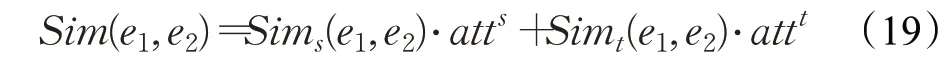
其中，atts和attt分别表示结构相似度和名称相似度的注意力权值。对于结构信息相对缺乏的长尾实体，DAT模型一方面通过路径学习获得了长尾实体的长关系结构依赖，另一方面通过名称编码补充了实体的名称语义，因此在处理长尾实体方面有较好的性能。

3.3 基于图的模型

基于图的模型同样认为知识图谱中的单跳信息只能获取实体片面的语义，与基于路径的模型不同，基于图的模型采用了一种邻域发现的视角，通常使用图神经网络作为编码器来捕获子图结构。图神经网络本质是根据消息传递规则将来自邻域的信息聚集到目标节点，让具有相似邻域的实体在嵌入空间中彼此靠近，在捕捉图的全局或局部结构信息方面表现优异。

（1）GCN-Align

GCN-Align[121]是第一个提出用图神经网络完成实体对齐任务的模型。该模型使用两个图卷积网络GCN分别处理两个待对齐的知识图谱，两个GCN 通过共享权重矩阵将来自不同知识图谱的实体嵌入到统一的向量空间中，借助实体之间的结构来传播对齐关系。此外，GCN-Align还组合属性信息和结构信息来共同学习实体表示，实体表示更新公式定义为：

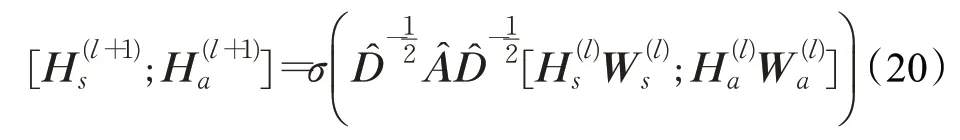
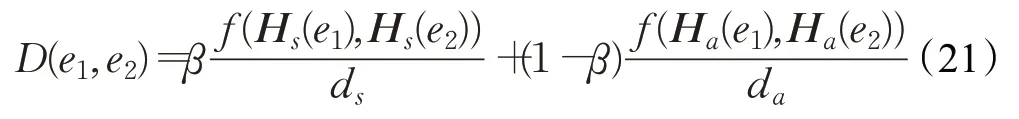
其中，Hs(e1)表示实体e1的结构嵌入向量，ds和da分别表示结构嵌入维度和属性嵌入维度，β用于衡量两种嵌入的重要性。

（2）NAEA

NAEA[122]提出在编码模块融合知识图谱的关系级和邻域级信息来表示实体，关系级和邻域级信息分别通过TransE和图注意力网络GAT捕获。给定事实三元组(h,r,t)，其邻域级表示的评分函数为：

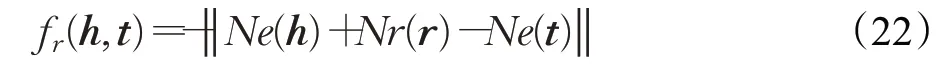
其中，Ne(·)和Nr(·)分别表示邻域级的实体表示和关系表示。在对齐模块，NAEA与BootEA模型类似，同样将实体对齐任务描述为一对一分类问题，使用实体分布的交叉熵损失训练优化。NAEA 通过不同权重组合邻居节点信息来学习邻域级表示，使实体不仅能够捕捉到邻居对自己的不同影响，而且能够关注邻域具有不同重要性的特征表示。

（3）RDGCN

上述两种基于图的模型存在着无法捕获知识图谱复杂关系信息的缺陷。Wu等人[123]提出了关系感知对偶图卷积网络RDGCN来充分利用关系信息。具体来说，RDGCN 将两个待对齐知识图谱编码到同一个语义空间，通过对齐关系将G1、G2合并成原始图Ge，并构造对偶图Gr如下：对偶图Gr的节点定义为Ge的边，若Ge中的两个边共享相同的头或尾实体，则在Gr相应节点之间添加边，Gr中的边权重表示共享头尾实体的百分比。为了捕捉原始图和对偶图之间的交互，RDGCN为每个原始-对偶交互定义了一个原始注意层和一个对偶注意层组成：利用原始图Ge的节点特征计算对偶注意层的注意力权重，利用对偶图Gr的节点嵌入计算原始注意层的注意力权重。此外，为了控制噪声在各层的累积，保留从交互作用中学到的有用关系信息，RDGCN在GCN 各层之间引入门机制。为了更好地利用不同KGs 中的实体名，RDGCN 使用预先训练好的英文单词向量构造原始图的输入实体表示。

（4）AliNet

AliNet[124]指出：来自不同知识图谱的对齐实体对可能具有非同构的邻域结构，这对以捕获实体之间邻域结构为核心的基于图的模型来说是巨大的挑战。AliNet引入远邻居来扩展对齐实体对邻域结构之间的重叠，旨在以端到端的方式缓解邻域结构的非同构问题。AliNet 首先利用GCN 学习实体的一跳表示；针对实体的远邻居，采用了一种类似图注意力网络GAT 的学习方式，以两跳邻居为例，其针对远邻居的实体表示更新公式为：

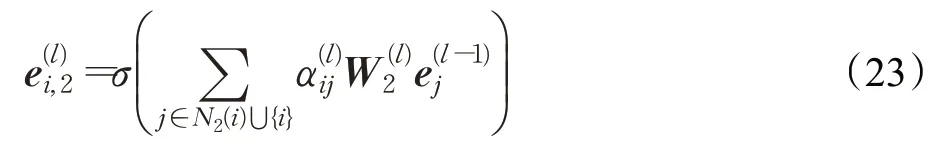
（5）其他基于图的模型

除了上述4种基于图的模型以外，GMNN[125]将实体对齐任务表述为一个图匹配问题，并在引入主题实体图概念基础之上，使用GAT 匹配两个主题实体图中的所有实体，得到图级别的匹配向量；MuGNN[126]使用AMIE+构建更密集的知识图谱，利用注意力机制对整个图形特征建模，从而将种子对齐信息传播到整个图形上；AVR-GCN[127]不同于传统GAT 进行邻居特征融合，而是在卷积过程中引入TransE模型的翻译特性，将实体的不同邻居加入对应的关系向量进行合并表示，使关系更直接地纳入模型中，但是通常需要额外提供先验的对齐关系对；为了摆脱对对齐关系对的依赖，HGCN[128]使用GCN 学习的实体嵌入来近似关系表达，并增加门机制来控制噪声在结构中的传播；KECG[129]通过联合训练一个基于GAT的交叉图模型和一个基于TransE的知识嵌入模型来协调知识图谱之间的结构异质性问题；HMAN[130]使用GCN和全连接网络来分别编码知识图谱的结构特征、关系特征和属性特征，同时将预训练模型BERT纳入框架，进一步提高对齐性能。

3.4 小结

实体对齐任务基准数据集的相关统计信息由表5给出。

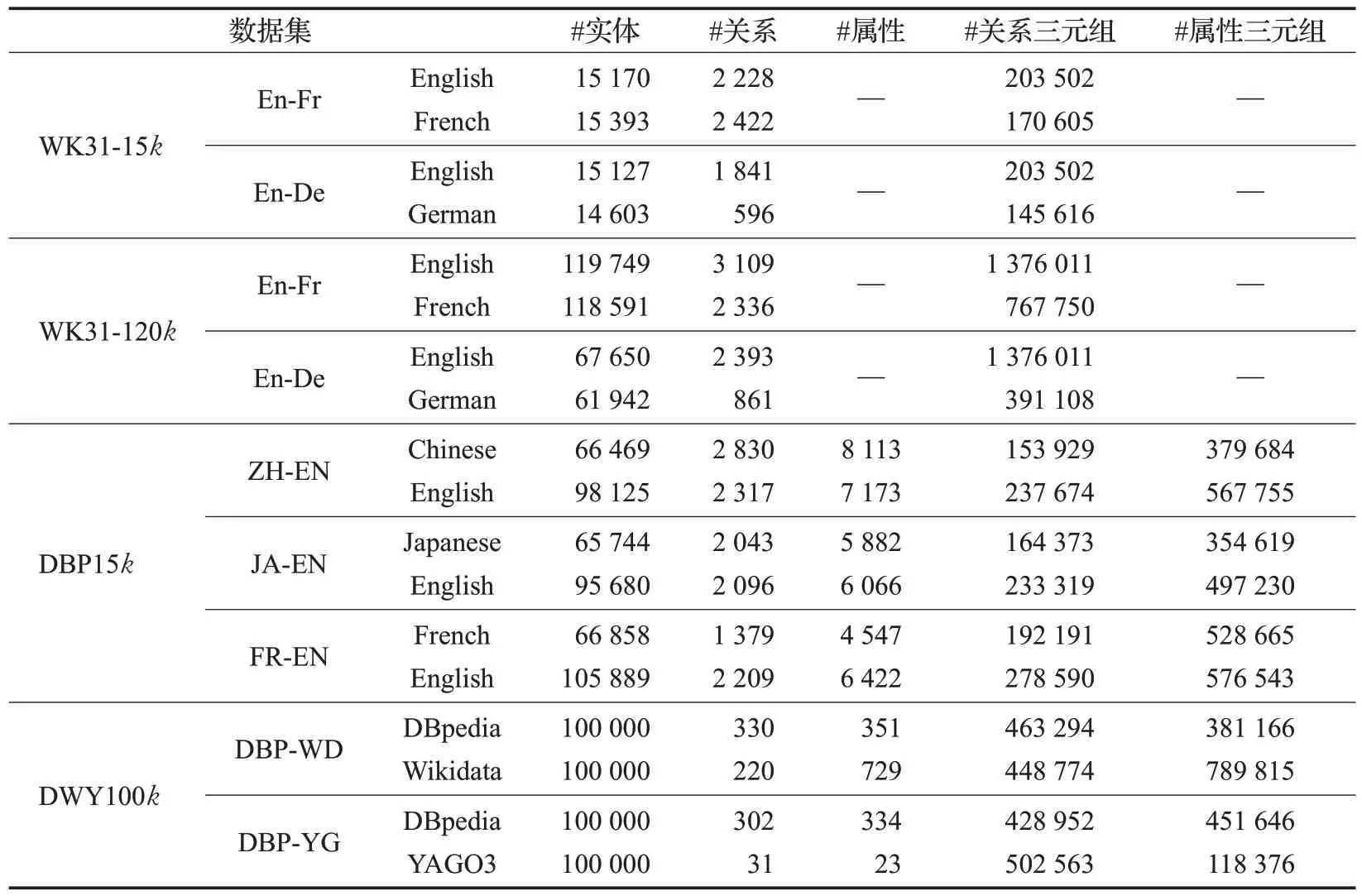
表5 实体对齐数据集统计信息Table 5 Statistics of datasets forentity alignment task

（1）DBpedia 是一个大规模的多语言知识图谱，包含从英文实体到其他语言实体的跨语言链接（interlanguage links，ILLs）。Sun 等人[110]分别从英文、中文、日文和法文中提取了至少包含4 条关系三元组的常用实体，并通过获取相关实体的关系三元组和属性三元组，构造了DBP15k数据集。

（2）WK31是从DBpedia的Person域中提取的，包含英文、法文、德文的三语知识图谱，由DBpedia本体的多语言标签和ILLs提供对齐信息。Chen等人[106]通过调整知识图谱中包含的实体数量，构造了WK31-15k和WK31-120k两个不同大小的数据集。

（3）DWY100k由Sun等人[107]构造，包含从DBpedia、Wikidata和YAGO3提取的两个大规模数据集DBP-WD和DBP-YG。其中DBP-YG具有不平衡的关系数，给面向多个知识图谱的实体对齐模型带来了更多的挑战。DBP15k和DWY100k中，属性三元组占很大比例。

与链接预测任务类似，实体对齐模型的整体性能指标包括：（1）MRR，所有正确对齐实体的平均倒数排序；（2）Hits@k，排序位于前k的正确对齐实体的比例，k通常取1、5、10。

基于三元组的模型依赖丰富的关系三元组来对齐实体，模型效率高、直观，但在缺乏结构信息的长尾实体上表现较差；基于路径的模型通过将关系三元组链接到长关系路径来扩展基于三元组的嵌入，由于路径数量远远超过关系三元组数量，导致基于路径的模型需要较长的训练时间；基于图的模型可以更充分地利用先验对齐关系，但不能克服知识图谱的异构性问题，且大多数基于图的模型（例如，HGCN、RDGCN）严重依赖实体名称来初始化嵌入模块中的节点嵌入，在没有实体名称的情况下，会显著影响实体对齐的准确性。

此外，模型的实体对齐性能还受种子实体对大小、是否利用辅助信息以及采用何种自举策略的影响。AttrE和MultiKE取得了目前公布的最先进结果，即使在种子实体对较少的情况下，依然能有不俗的表现。这是因为它们充分利用了如属性和关系谓词等各种类型的信息。然而使用辅助信息提高实体对齐性能通常会增加训练时间，需要平衡模型的有效性和效率。表6从编码模块、距离度量、附加信息和训练方式等方面给出了上述26种实体对齐模型的对比。

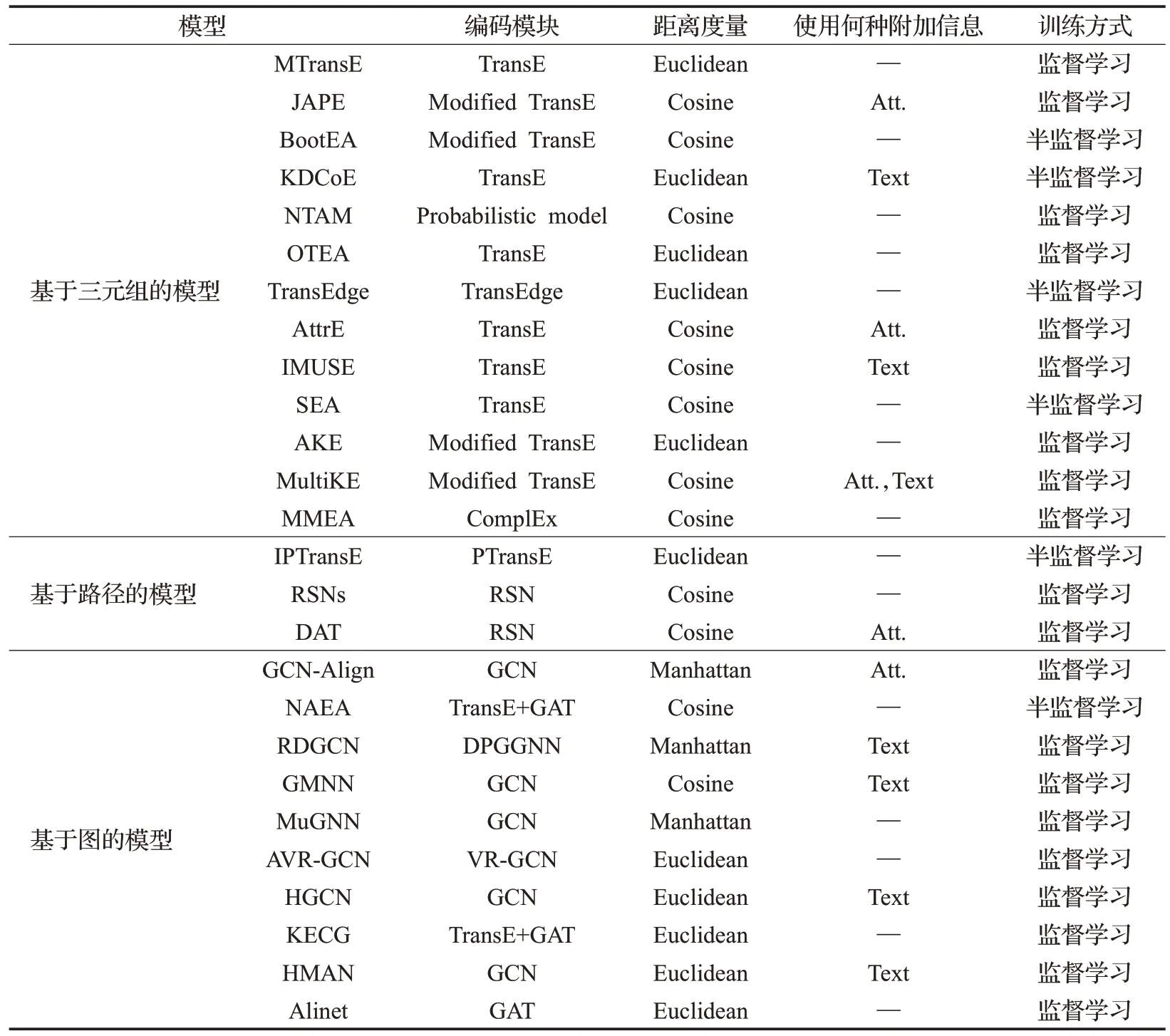
表6 面向多个知识图谱的实体对齐模型总结Table 6 Summary of entity alignment models oriented to multiple knowledge graphs

4 未来研究方向展望

知识图谱嵌入模型的大量研究，促进了其在下游系统中的成功应用。但是现有研究中仍然存在几个悬而未决的问题和挑战，尚有不少充满希望的未来研究方向。接下来将主要从三个方面展望知识图谱嵌入研究：（1）从提升知识图谱嵌入性能的角度，包括“长尾实体学习”“多模态知识图谱研究”和“System I与System II融合研究”；（2）从丰富知识图谱嵌入内容、扩充知识图谱嵌入应用的角度，包括“时序知识图谱研究”和“领域知识图谱研究”；（3）从知识图谱嵌入模型评价角度，包括“可扩展性研究”。

（1）长尾实体学习

如前分析，现有的知识图嵌入模型往往需要大量高质量的样本进行训练和学习，因此长尾实体学习一直是困扰知识图谱嵌入模型性能的关键问题之一。由于缺乏结构信息，大多数仅依赖于结构信息的知识图谱嵌入方法往往存在对长尾实体表示能力不足的缺陷。一种典型的思路是通过增加辅助信息，加强语义表示。近年来，one-shot和zero-shot学习在计算机视觉、自然语言处理等领域引起了广泛关注。未来可以设计一种新的知识图谱嵌入框架，使之更适合于从知识图谱中推测新的事实，并更有效帮助跨知识图谱的实体对齐任务。

（2）多模态知识图谱研究

尽管关系三元组作为知识图谱的内部信息，已经被目前的知识图谱嵌入模型很好地组织起来，然而这些模型在链接预测、实体对齐等实际应用中的性能还远远不够。事实上，知识图谱中的实体和关系包含着复杂的特征和丰富的语义信息，尚未得到充分的挖掘。已有的一些模型尝试结合实体类型、关系路径、属性信息或者实体描述，均取得了比仅仅学习三元组完成知识表示更好的性能，这进一步验证了多模态信息之间是互补的猜想，即：尽管模态异构，但是语义关联。围绕多模态知识图谱的工作近几年已在相继展开。Wang等人[131]通过向文本实体分发多样图像并设置视觉语义关系，构建了全面的多模态知识图谱Richpedia；Wang 等人[132]研究了包含视觉三元组的场景图关系抽取。多模态知识图谱也能为下游系统提供更丰富的包括文本、图像、视频等内容。未来可以进一步针对视觉信息，开发多模态语义融合来完成知识表示学习，以提升嵌入性能。

（3）System I与System II融合研究

System I 和System II 是认知科学中的双通道理论，分别代表了神经学派和符号学派的研究思维。现有的大多数以学习实体分布式表示为目的的知识图嵌入模型均属于System I的范畴，还有一些研究通过逻辑规则（例如一阶谓词逻辑、规则库等）实现链接预测和实体对齐任务，这些方法属于System II的范畴。Rossi等人[91]在比较现有链接预测模型时发现：基于规则的AnyBURL模型是一个非常具有竞争力的模型，因为它被证明优于大多数面向单个知识图谱的嵌入模型，且计算速度很快。Sun 等人[133]在比较现有实体对齐模型时也发现了近乎同样的结论：基于规则的LogMap 模型和PARIS 模型在实体对齐性能上优于几乎所有面向多个知识图谱的嵌入模型。这也为知识图谱嵌入模型提出了非常严峻的考验。一个直觉的研究思路是进行System I 与System II 融合研究。Qu 等人[134]率先尝试了这种研究思路并提出了RNNLogic模型，该模型将逻辑规则看作一个潜在变量，同时训练规则生成器和逻辑规则的推理预测器，取得了SOTA的效果。未来研究可以进一步拓展System I与System II的融合。

（4）时序知识图谱研究

现有的知识图谱嵌入模型主要集中在静态知识图谱上，即假设事实三元组(h,r,t)不随时间迁移而变化，然而，这种假设忽视了非常重要的时间信息。一方面，结构化的知识只在特定的时期内成立，例如（?，thePresidentOf，USA）的头实体并不是一成不变的，每位总统都有其对应的任期，不考虑时间信息的知识表示容易导致事实之间的矛盾。另一方面，事实的演变遵循时间顺序，包含时间信息的知识图谱嵌入能够挖掘更多的时间规律。

已有一些前期工作尝试进行时序知识图谱的嵌入模型研究，与以往的静态知识图谱不同，时序知识图谱嵌入旨在同时学习时间嵌入和关系嵌入。Lacroix 等人[135]在原有三元组基础上增加时间维度，将知识图谱描述成四元组的集合，并提出了四阶张量分解模型；Goel等人[136]提出了时序嵌入函数，为时序知识图谱在任何时间点的实体提供了一个隐藏的表示，该嵌入函数可以与任何静态知识图谱嵌入模型相结合。但是现有模型只能学习看得见的时间戳，无法推广到未观测时间域。未来研究可以着眼于针对时间戳的表示，来实现面向事实的时间预测。

（5）领域知识图谱研究

现有的模型研究都仅仅应用于通用知识图谱上，很少有研究对领域知识图谱嵌入进行分析。一方面由于领域知识图谱对专业性与准确度的要求高，这也要求其必须有严格的本体层模式。另一方面，相对通用知识图谱而言，领域知识图谱中关系三元组数量较少，通用的知识图谱嵌入方法不能很好的完成知识表示学习。此外，领域知识图谱与通用知识图谱的实体对齐问题尚处于空白。如何针对领域知识图谱构建统一的嵌入空间成为亟待解决的问题。

（6）可扩展性研究

可扩展性在大规模知识图中至关重要，随着知识图谱数据量日趋增大，模型的可扩展性问题显得愈发紧迫。由于模型的计算效率和表达能力之间存在相互制约的关系，因此为了追求表达能力，目前仅有有限数量的研究将模型应用于超过100万个实体的知识图谱上，大多数方法都只能适应小规模知识图谱嵌入，难以扩展到数百万个实体和关系。所以，为了处理复杂的深层架构和日益增长的知识图谱，需要将运算效率如时间复杂度和空间复杂度等纳入模型的考量范畴。

5 总结

本文从任务驱动的角度，将现有知识图谱嵌入研究分为面向单个知识图谱的链接预测研究和面向多个知识图谱的实体对齐研究两大类。进一步根据知识图谱嵌入模型的内在假设和实现方法的不同，将面向单个知识图谱的链接预测模型分为距离模型、翻译模型、语义匹配模型、神经网络模型和几何模型五类；根据编码模块捕获语义的层次，将面向多个知识图谱的实体对齐模型分为基于三元组的模型、基于路径的模型和基于图的模型三类。本文在分别列举分析了各类模型的优缺点基础之上，探讨了现有知识图谱嵌入技术存在的问题，对知识图谱嵌入模型的未来研究方向提出了展望。