电力隧道工程建设中的离散时间费用权衡问题

熊 俊， 孙 聪， 刘 青， 马博翔,3， 张立辉

(1. 国网北京市电力公司， 北京 100041； 2. 华北电力大学 a. 经济与管理学院； b. 新能源电力与低碳发展研究北京市重点实验室， 北京 102206； 3. 清华大学 电气学院， 北京 100084)

当前我国处于基本建设大发展时期，大量的重复性建设项目如隧道工程、地铁等正在兴建或规划之中，这些项目投资大、工期长，因此对它们的研究具有很实际的意义。重复性建设项目是指在建设工程的每个单元各个工序不断重复进行的项目[1]。由于工作连续性和资源恒定性是重复性建设项目调度计划中需重点考虑的因素。因此，近年来，国内外学者对两者进行了大量的研究，例如Vanhoucke[2]提出工作连续性约束能使每个工序的施工空闲时间最小化，这在一定程度上能缩短工期；而Birrell[3]提出维持工作连续性将导致工期变长； Selinger[4]也认为不保持工作连续性将有可能进一步缩短项目工期。Zhang等[5,6]提出资源恒定性约束有利于高效利用资源，但同时也可能造成工期的延长，其还研究了资源连续性的相关原理。因此，有必要权衡工作连续性与资源恒定性对离散时间费用权衡(Discrete Time-Cost Trade-off Problem，DTCTP)的影响，但目前相关研究较少。DTCTP是项目调度中的一种双目标优化问题，属于强NP - 难问题[7]。DTCTP的解决方法主要有基于动态规划[8]和分支定界的精确算法[9]，也有基于启发式规则的各种启发式算法[10]以及智能算法[7,11]。目前对该问题的研究大都采用智能算法求解，如Hyari等[12]构建了能权衡总工期与总费用的遗传算法，并采用Pareto最优性原理对重复性建设项目的调度方案优化；Zhang等[1]用遗传算法解决了软逻辑下重复性项目的时间费用权衡问题；Long等[11]设计了考虑工序优先关系和工作连续性的遗传算法，并将其应用于优化重复性项目的工期和费用。但是，针对工作连续性和资源恒定性的算法还有待进一步研究。所以，本文作者通过探索项目施工过程中工作、资源与时间费用问题的内在关系，构建隧道建设中关于工作可间断和资源可波动的离散时间费用权衡模型(DTCTP-wr)，提出一种双链式整数编码和随机单点交叉算子的改进算法，并以一个实际的电力隧道建设项目为例，验证算法的有效性和合理性，并得出工作连续性约束和资源恒定性约束对项目造成的影响。而且，该算法也能移植到其他重复性项目的调度中，为我国基础设施建设提供更为科学、经济的调度方案。

1 DTCTP-wr

1.1 问题描述

重复性项目问题描述如下：设有N个工序，每个工序有M个相同的单元(例如，隧道具有多个相似的竖井)。工序1是开始工序，工序N是结束工序。工序i(i=1,…,N)的施工情况与它的紧前工序有关，需与紧前工序满足结束 - 开始的时间约束。工序i的第j单元表示为子工序aij，并且有Ki种执行模式。aij的工期用dijk,k=1,2,…,Ki表示，变量k表示执行模式选择。

项目的总费用由以下部分组成：直接费用DC，间接费用IC和所有工序的资源闲置费用IRC。各部分费用具体计算如下：

采用式(1)计算项目直接费用DC，由项目中每个工序各单元的材料费用MC、劳动力费用WC、设备费用EC之和构成。

DC=MC+WC+EC

(1)

采用式(2)计算项目间接费用IC，由项目中每天对应的费用之和构成。

(2)

式中：ICRd为第d天的间接费用；D为项目的总工期。

采用式(3)计算资源闲置费用IRCi。资源闲置费用是由于承包商执行模式选择不当，造成资源闲置所产生的费用。若工序i须保证资源恒定性约束，IRCi等于所选择执行模式的劳动费用率(包括人、料、机的闲置费)与中断天数的积。否则，若工序i无资源恒定性约束，IRCi等于所有可选执行模式中劳动费用率最高值与中断天数的积。

(3)

式中：xijk为二进制数(如果子工序aij在模式k下执行，xijk取1；否则，xijk取0)；INTi为工序i的中断天数；Ri为工序i资源恒定性约束；集合Θ表示所有工序的资源恒定约束关系。

1.2 数学模型

目标函数：

MCij+IRCi]+IC

(4)

约束条件：

sij+dij≤spj,p∈(j,N],i=1,2,…,N;j=1,2,…,M

(5)

(6)

(7)

(8)

(9)

xijk-xi(j+1)k=0,i∈Θ;j=1,2,…,M-1;k=1,2,…,Ki

(10)

(11)

Ft≤Tmax

(12)

式中：i为工序数；j为单元数；N为工序总数；M为单元总数。目标函数式(4)最小化项目总成本。约束条件式(5)表示在同一工序中子工序aij完成后子工序ai(j+1)才可能开始，sij为子工序aij的开始时间。约束条件式(6)中dij指工序i单元j的持续时长。约束条件式(7)中yijl指工序i单元j选择第l种模式时yijl=1。约束条件式(6)(7)要求每一工序需满足给定的逻辑施工顺序，即子工序ai(l+1)只能在子工序ail结束后才能开始(如果子工序ai(l+1)满足条件，yijl取1；否则，yijl取0)。约束(8)表示每个子工序只能有一种逻辑调度顺序。约束(9)表明为了满足工作连续性约束，中断时间必须为0，集合Φ表示所有工序的工作连续性约束关系。约束条件式(10)要求所有满足资源恒定约束的工序均需执行同样的执行模式。约束条件式(11)表示任一子工序仅有一种施工顺序，同一工序内的任何两个子工序不能同时施工。约束条件式(12)要求项目的工期Ft不能超过给定的最大工期限制Tmax。

2 改进遗传算法

由于DTCTP问题的计算规模相当大[7]，非线性方法很难在短时间内得到令人满意的结果。因此，针对所研究的问题，本文设计了相应的双链染色体编码方式、带惩罚函数的适应度值计算法，以及单点交叉算子和变异算子，并最终提出了一种具有求解能力的改进遗传算法。

2.1 双链染色体编码

图1 染色体结构

2.2 适应值计算

对于DTCTP-wr，在调度方案集中有可能存在一些总工期超期或总费用超额的方案。所以本文提出了一种惩罚机制，确保这些方案比在工期范围内的项目适应度值小。对于个体I,Ft(I)为个体I对应的最小总工期。修正其最小总工期目标函数为：

F′c(I)=(1+βt)Fc(I)

(14)

式中：βt为一个正惩罚因子，按式(15)计算。

(15)

因为DTCTP-wr属于最小化双目标问题，所以适应度函数应转化为：

fc(I)=max{F′c(1)，F′c(2),…,F′c(P)}-F′c(I)

(16)

式中：P为种群规模。

适应度值确定后，接下来就选择当前代的最优个体进行迭代遗传操作。

2.3 单点交叉算子

对执行模式链进行单点交叉操作。令随机整数r(0≤r≤N)作为单点交叉起点。工序i=1,2,…,r所在的染色体，从一个父代中得到染色体片段，即

(17)

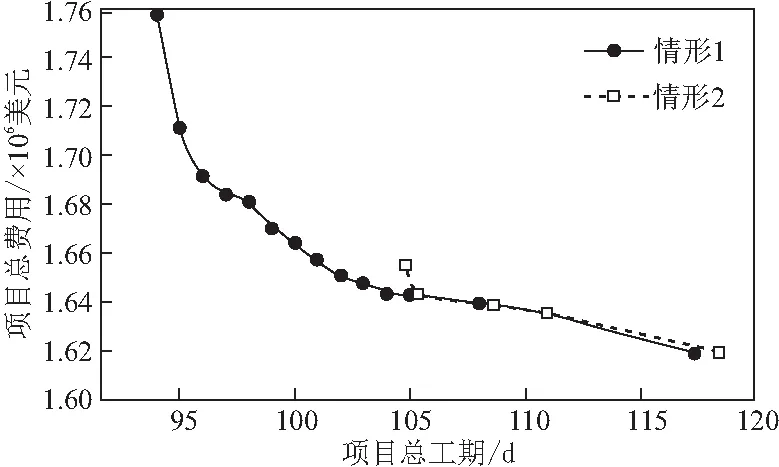
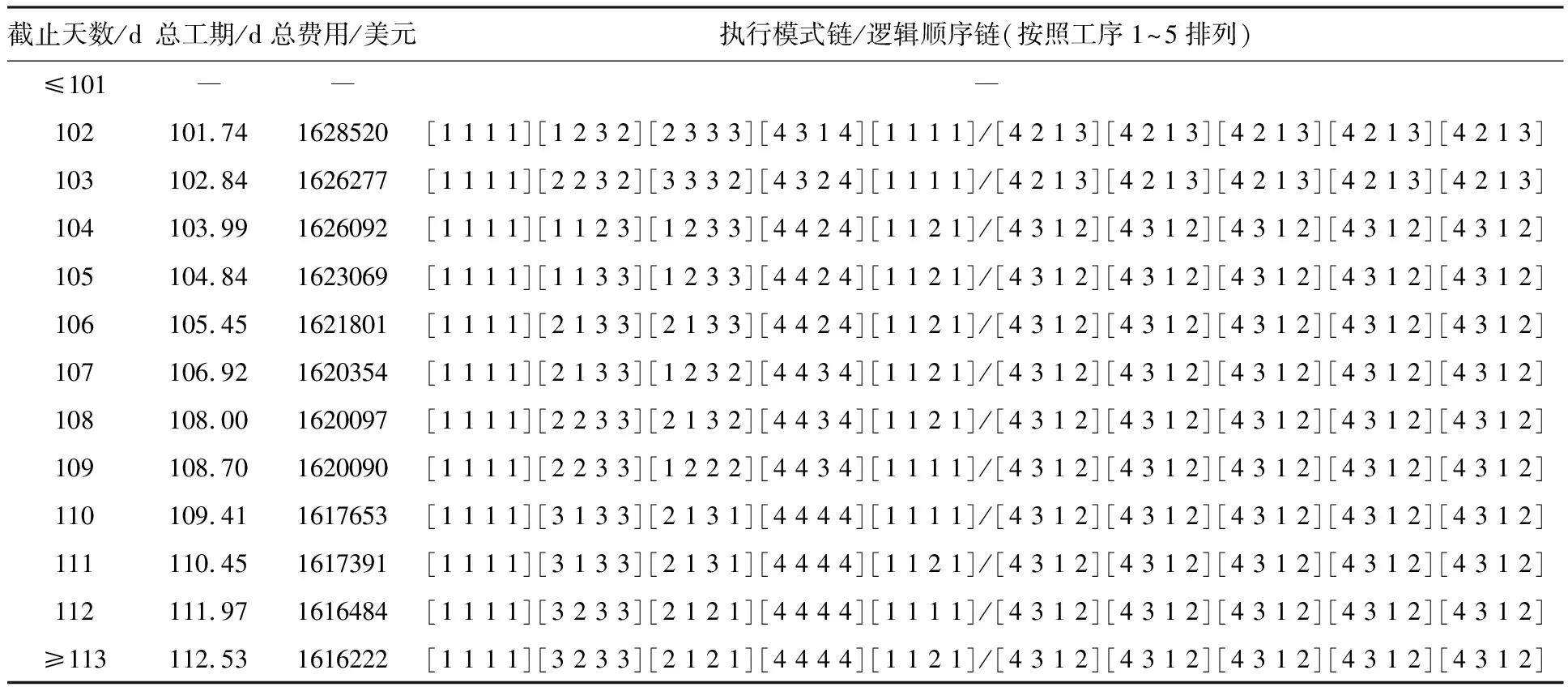
工序i(r

(18)

与执行模式的单点交叉操作方法类似，逻辑顺序链也用同样的方法，但须注意的是单点交叉点的位置需要重新随机生成。

2.4 变异算子

对于执行模式链，随机选取工序t，t∈[1,N]作为突变点。若工序t有资源恒定性约束，那么，工序t所在的染色体片段需在随机整数[1,Kt]取值。否则，保证工序t中有且仅有一个单元在[1,Kt]随机取值即可。

对于逻辑顺序链，首先选出变异的工序t，即随机生成整数t，t∈[1,N]；然后，选出工序t所在的变异单元，即生成两个随机整数u,v,u,v∈[1,M]；最后，将工序t的第u单元的染色体信息与第v单元的染色体片段信息交换。

2.5 调度算法

为了将每个染色体中的信息整合为与工期相关的信息，进而求得其对应的总工期和总费用。对于给定个体I，调度算法具体步骤如下。

步骤1：初始化种群P，种群大小为Np，设当前遗传代数gen为1 ；

步骤2：通过模型中的约束条件解析执行模式链和逻辑顺序链，计算子工序aij的工期dij并根据模型中的约束条件得到当前代的最小总费用。根据所要求解的子问题计算所有个体的适应度值，然后对种群进行轮盘赌选择，生成子种群C；

步骤3：对子种群C中的所有个体进行交叉算子，生成新的子种群C1；

步骤4：对子种群C1中所有个体执行变异算子，生成新的子种群C2；

步骤5：分别从种群P和子种群C2中各挑选适应度较高的1/2个体进行合并得到新的种群P；

步骤6：令gen=gen+1，若gen的值小于设定的最大遗传代数，返回步骤2；否则跳出程序并输出近似最优解。

3 结果及分析

本文采用一个明开电力隧道建设项目作为算例[13]。该项目由五个工序构成，分别是挖隧道，填地基，做竖井，上盖板和铺顶面。项目管理费用为2500美元/d。项目其他基本信息如表1所示。dijk可通过dijk=Qij/Pik得到。下面将通过四种情形进行讨论：

情形1: 所有工序没有工作连续性约束，但均有资源恒定性约束；

情形2: 所有工序都有工作连续性约束和资源恒定性约束；

情形3: 所有工序均有工作连续性约束，但没有资源恒定性约束；

情形4: 所有工序没有工作连续性约束，同时也没有资源恒定性约束。

表1 项目基本数据

3.1 工作可间断影响分析

图2 有/无工作连续性约束下时间 - 费用曲线

图2为有/无工作连续性约束下时间 - 费用曲线，通过比较情形1和情形2的结果可知，在资源恒定性约束情况下，工作可间断对项目成本和时间的影响。(1)如图2所示，总工期范围在106～118 d内，情形1，2的时间 - 费用权衡曲线基本上是重合的。这是由于在该隧道建设项目中，只有当所有工序都没有中断或存在很少中断的情况下才会出现项目工期较长的情况。(2)如图2所示，情形1得到的方案数明显比情形2多， 这是因为不考虑工作连续性，子工序与子工序之间的时间关系将更加灵活，约束时间不再必须取0。(3)表2，3分别为情形1，2下时间 - 费用曲线的详细计算结果。据表2，3可知，两种情形下主要的区别在于方案中的最小项目总工期。表3列出了情形2下详细的计算结果，其中最小项目总工期为104.82 d，对应的总费用为1654977美元。如果所有工序允许工作不连续(情形1)，最小项目总工期将缩短为94 d，相比节约了10.32%；但是对应的费用相应也提高到了1758235美元。情形3，4也有相似的结论，具体结果分别见表4，5。可见，允许工作中断将有利于项目缩短总工期。

3.2 资源可波动影响分析

图3为有/无资源恒定性约束下时间 - 费用曲线,通过情形1和情形4的结果比较可知，在没有工作连续性的情况下，资源可波动对项目成本和时间的影响。(1)如图3所示，在最大工期限制范围内，每个可行的项目方案，情形4中的总费用总是低于情形1。这种现象可解释为：当工序不需维持资源恒定性约束时，该工序中所有的子工序都不会对项目工期造成影响，并且将会选择最经济的执行模式。但是，当所有工序有资源恒定约束，子工序需要根据其他相关子工序执行模式选择情况来选择类似的执行模式，而对其他子工序经济的执行模式并不一定适用于该子工序。(2)根据图3，结合对比表2，5中的项目总费用可知，当截止日期为Tmax=94 d时，这两种情形下的项目总费用差值达到最大值(1758235-1723960)=34275美元。因为总工期越短，中断天数越少，不考虑资源恒定性的情形4下，对应的资源闲置费用就越低，而情形1中资源闲置费用也会降低，根据公式(3)可知，中断天数的变化在这一阶段对资源闲置费用起主要的影响；(3)据表2，5可知，当所有工序没有资源恒定性约束时的最小项目总费用1615909美元，而满足资源恒定性约束时最小总费用为1618868美元，两者基本相等。而对应的总工期前者仅113 d远少于后者的118 d。情形2，3也有相似的结论，具体的结果分别见表3，4。可见，取消资源恒定性约束将有利于项目减少总费用。

3.3 双重因素组合影响分析

通过情形2和情形4的结果比较可知，工作可间断和资源可波动双重因素影响下对项目成本和时间的影响。(1)据表3和表5可知，情形2的可选择方案数明显少于情形4。主要原因有两点，一是因为情形2考虑工作连续性后，子工序与子工序之间的时间约束比情形4强，因而导致情形2中部分方案丢失，二是因为资源恒定性要求，子工序之间必须选择同一执行模式，这样也大大减少了可选的方案。(2)对比观察表3，5可知，当选择总费用相差不大的方案时，在表3选择总费用为1619612美元的方案，对应表5与之最接近的总费用为1619954美元的方案，前者的工期比后者长(118.48-108.41)=10 d。当选择总工期相差不大的方案时，在表3选择总工期为104.82 d的方案，对应表5与之接近的总工期为104.89 d的方案，前者的总费用比后者高(1654977-1622063)=32914美元。因此，对于工作连续性和资源连续性的选择，项目管理者应根据具体的项目目标制定与之契合的方案。

表3 情形2下时间 - 费用曲线的详细计算结果

图3 有/无资源恒定性约束下时间 - 费用曲线

表4 情形3下时间 - 费用曲线的详细计算结果

表5 情形4下时间 - 费用曲线的详细计算结果

4 结 论

(1)构建了工作可间断和资源可波动的离散时间费用权衡优化模型(DTCTP-wr)，并通过一个实际的电力隧道工程建设项目验证了其可用性和合理性。

(2)结合研究的问题，提出了基于双链式整数编码和随机单点交叉算子的改进遗传算法。该算法在确保近似最优解的条件下有效地减少了运算量，并且只要稍加扩展与完善就可用于国家基础建设项目的规划中。

(3)定量验证了允许工作间断有利于项目缩短总工期；允许资源波动有利于减少项目总费用。在考虑工作可间断和资源可波动双因素的影响下，管理者可根据项目的具体要求有针对性地得到最佳的项目调度方案。