盾构施工地层损失控制方法及实例

罗兴财， 周小文, 张盛红

(1. 中铁南方投资集团东莞公司， 广东 东莞 523037； 2. 华南理工大学 亚热带建筑科学国家重点实验室， 广东 广州 510640)

在城市地下隧道施工中，地面沉降的控制一般具有较严格的要求。尤其在地质条件较差、隧道浅埋的情况下，沉降控制非常困难。城市地下隧道常采用盾构法施工，过程往往伴随一定的地面沉降，主要是由地层损失和盾构周围土体受扰动或破坏后的变形再固结造成的，其中前者占主要成分。工程设计和施工中，一般需根据周边建筑物环境提出地面沉降的控制指标。但是，如何实现沉降控制，则较为复杂，没有规范指导，有时候难度很大，控制效果一般取决于施工单位的经验和水平。盾构掌子面和盾尾注浆的施工工艺和参数对于地层变形都有重要影响。王海刚[1]研究了盾尾注浆压力的波动对地表沉降的影响，认为考虑注浆压力的波动时，隧道轴线上方的地表沉降在确定性分析结果增减60%的范围内，可见盾尾注浆参数具有显著影响。虽然施工单位一般会尝试利用地层损失去控制地层沉降，但由于对地层损失的形成机理、影响因素与预测计算的掌握不够，实际上又很少去对地层损失做较准确的控制。一般是基于以往模糊的经验，选取掌子面操作和盾尾注浆等施工参数，然后通过实测的地层沉降来调整施工参数，沉降控制有时候表现得像撞大运。

实际隧道工程经常出现过大地面沉降或造成周围既有建(构)筑物损害的工程事故。因此，如何尽可能定量地利用地层损失的控制去进行地层沉降的控制，是值得深入研究的。

广州市某盾构隧道工程，由于要下穿已有的城际隧道，对地层沉降控制提出了较严格的要求。在该工程施工中，对如何计算和选取地层损失进行了较深入的分析研究，施工前根据地层沉降控制要求先预测和选择地层损失，施工中通过掌子面及盾尾注浆参数的调控来控制渣土出土量，再通过沉降监测对地层损失进行反分析和优化施工参数，最终较好地控制了地层沉降，未对既有上部隧道造成影响。本文较全面地总结了地层损失的计算方法及其在该工程中的应用情况，期望该工程案例对类似工程具有参考作用。

1 地层损失的概念

1969年，国外学者Peck[2]率先提出地层损失的概念，认为不排水条件下隧道开挖导致的地面沉降槽体积与地层损失相等，并由此提出了描绘地面钟形沉降槽的经验公式，其原理如图1所示。

由图1可知，Peck定义的地层损失为实际开挖范围体积和建成隧道体积之差。刘建航[3]、潘昌实[4]、姜忻良等[5]认为地层损失不应计入排水固结引起的土体压缩量，故地层损失应等于开挖土体体积与包括隧道外围注浆层体积的竣工隧道体积之差。Loganathan[6]、缪林昌[7]等则认为地层损失可分为两个阶段，即施工阶段不排水变形的地层损失与竣工后排水固结和蠕变变形造成的地层损失。鄢豪杰等[8]采用基于分数阶的土本构模型计算隧道竣工后的固结沉降，分析了隧道衬砌为半透水边界条件下隧道开挖引起的工后长期变形，认为隧道衬砌的渗透性(造成隧洞外的土体渗流)对长期沉降的影响不可忽略，衬砌的渗透系数越大，沉降值也越大。该结论似也意味着地层损失应该考虑工后固结变形引起的沉降。张盛红[9]对不同阶段地层损失的含义以及估算方法做了分析。

综合国内外的研究可以看出，对是否将工后排水固结，以及是否考虑土体蠕变和隧洞衬砌渗漏等引起的土体压缩变形计入地层损失尚存在一些分歧。鉴于工后地基变形的复杂性以及仍然认为施工期的地层损失占主要成分，本文按照主流观点，不考虑工后排水固结与蠕变等因素的影响，将地层损失由实际开挖土体量与包含注浆的竣工隧道体积之差进行计算。

实践中，衡量地层损失对临近结构的影响程度还常用地层损失率η来表示，计算方法如下：

(1)

式中：Vl为单位长度地层损失；r为隧道衬砌外半径。

2 地层损失的计算方法

地层损失的计算方法可分为理论计算法、经验公式法以及数值模拟计算法。理论计算法是假定地基为弹性半空间，隧道边界外土体发生均匀径向收缩，各点朝隧道中心移动，从而可计算地层损失，如Sagaseta[10]、Verruijt等[11]等皆提出了地层损失的理论公式。由于理论计算做了地基为弹性以及隧道边界收缩位移模式的假定，且难以考虑复杂地层情况，其计算结果与实际常有较大的差距。因此，目前比较常用的方法还是经验公式法和数值计算法。以下仅对经验公式法和数值模拟计算法做简要介绍和分析。

2.1 经验公式法

经验公式法来源于众多工程资料，对施工过程的物理力学变化进行简化及做适当假定，通过数理统计方法建立地层损失的计算模型。

(1)Peck公式法及其改进方法

Peck假定地层为均质土层，基于大量实测资料发现地表沉降沿隧道长度方向为均匀分布，沿横向呈类似正态分布的钟形曲线，参见图2，Peck公式如式(2)所示。

(2)

式中：x为距离隧道中轴线的水平距离；Smax为地层损失导致的最大地表沉降量；S(x)为位于x处的地表沉降量；i为地表沉降槽半宽度，即正态分布反弯点离中轴线的水平距离。

图2 Peck曲线

记单位长度地层损失为Vl，令其与沉降槽体积Vs相等，则地层损失由式(3)计算：

(3)

地表沉降槽曲线表示为：

(4)

由式(4)可得：

(5)

将Smax和i代入式(1)，可得地层损失率：

(6)

Peck公式原理简单，假定为正态曲线的沉降槽形状与实际工程的地表横向沉降形态符合较好，但该方法也存在一些缺陷，主要有：对地层条件考虑少，尤其不太适用于软弱地层；未反映隧道洞径以及埋深对地基变形机制的影响；沉降槽半宽度i不易确定。

针对Peck公式的不足，国内外学者做了大量的研究，提出了多个改进的计算方法，如：

Clough等[12]提出了饱和黏土地表沉降槽宽度系数i的计算方法：

(7)

式中:h为隧道埋深。

Attewell等[13]在公式中融入了地层特性、隧道埋深、隧道半径等参数的影响：

(8)

(9)

式中：k,n与地层参数、施工条件有关；A为开挖断面横截面积。

刘建航[3]考虑地基为多层土情况，提出了修正的i的计算方法：

(10)

Mair[14]通过开展离心机模型试验，提出隧道顶部任意深度处的地层沉降槽宽度的计算公式：

i=K(z)(h-z)

(11)

(12)

式中：z为隧道顶部以上某点深度(m)；K为沉降槽宽度参数。

姜忻良[5]基于观测数据和回归分析，提出了隧道顶以上任意深度处的沉降槽曲线：

(13)

(14)

(15)

总之，经过后人的大量研究，考虑地层性质、土体饱和度、隧道尺寸与埋深等的影响，对地表沉降槽曲线和宽度系数i的取值做了一些改进，提高了公式的适用性。

(2)间隙参数法

间隙参数法是一种利用综合的间隙参数对地层损失进行计算的方法，如Rowe[15]、Lee[16]等提出的地层损失计算公式，具体如下：

Vl=π(rg-g2/4)

(16)

g=GP+U3D+ω

(17)

式中：g为间隙参数；Gp=2Δ+δ为物理间隙，指盾构机的最大外径与隧道衬砌外径差值，若考虑注浆影响，一般取Gp=(7%～10%)(2Δ+δ)，其中，δ为衬砌安装需要的间隙；Δ为盾尾盾壳的厚度；U3D为由于盾构开挖的应力释放引起的土体变形；ω为由于人为因素(盾构姿态、掌子面压力波动、盾构机周围黏附土、盾尾间隙注浆效果等)造成的地层损失。间隙参数g的构成如图3所示。

图3 间隙参数g构成示意

2.2 数值模拟法

盾尾间隙是地层损失的主要来源。等代层法、位移收敛法和应力释放法是当前模拟盾构隧道施工引起的地层损失的数值计算方法。

等代层法是将盾尾间隙概化为均质、等厚的等代层来模拟地层损失。等代层的力学参数较难确定，一般由工程实测数据反演估算和经验确定，故此，等代层法灵活性较大，是一种很近似的计算方法。

应力释放法是将应力释放施加在隧道周边土体上，从而模拟地层损失引起的应力重分布。该法对地层损失物理意义的解释不够明确，且不如位移收敛法方便，因此目前运用很少。

位移收敛法与应力释放法施加力边界不同，该法是在给开挖面周围土体单元或衬砌单元施加强制的边界位移使其收敛到衬砌的外边界。通过控制间隙参数g的大小来实现对地层损失的模拟。根据盾构施工的多种可能情况，位移收敛法主要包括适合于模拟较大直径隧道开挖的月牙形渐变收敛模式与适合模拟中小直径隧道施工的圆环形均匀收敛模式二种。在盾构机向前掘进一环衬砌的距离后，让衬砌拱顶周围土体逐渐以月牙形或圆环形进行收敛，当达到间隙参数g时再激活衬砌单元，再进行注浆。

3 地层损失率经验范围值

地层损失受到不同因素的影响，如地层土质、设计与施工参数、盾构机特性、工程管理技术、水文地质等。不同地区的地质条件差异较大，这些因素对地层损失的影响也有一定的差异。因此，地层损失的取值也与地区经验及施工技术管理直接相关[9]。

刘建航[3]、魏纲[17]、吴昌胜[18]、朱才辉[19]等分别对盾构施工的地层损失做过统计分析，提出了地层损失率范围值。本文在此基础上结合自身经历的工程数据，综合提出地层损失取值范围如表1[3,17～19]所示。

表1 地层损失率地区经验值

4 某盾构隧道工程地层损失估算及沉降控制

4.1 工程概况

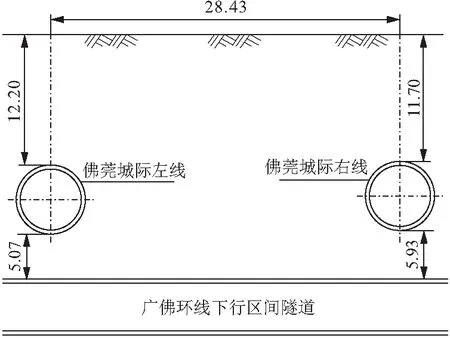
图4 隧道位置关系/m

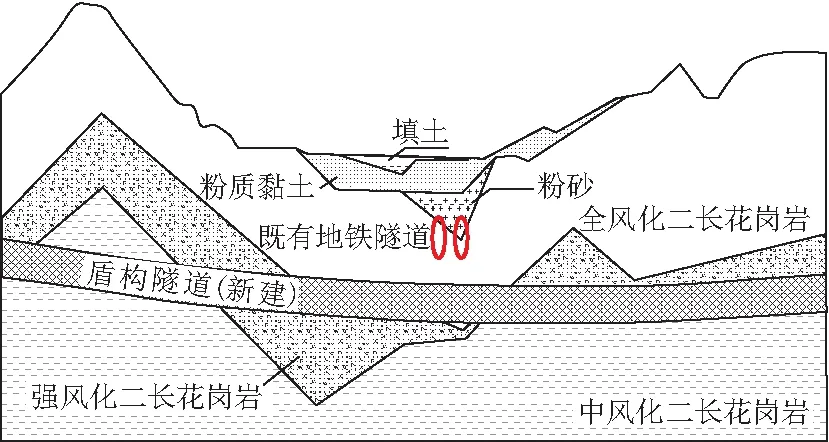
图5 隧道纵断面

广佛线某段盾构隧道下穿已运营的既有佛莞线隧道，佛莞线左右两隧道中心轴线相距28.43 m。新建隧道与上方佛莞线隧道净距为5.07～5.93 m，如图4所示。该段使用大型土压平衡盾构施工。纵断面及地层条件见图5。既有佛莞线隧道的上覆土厚度为11.7～12.2 m，衬砌内、外径分别为7.7，8.5 m。下穿施工的广佛线隧道衬砌内、外径分别为8.0，8.8 m。在下穿区域，新隧道的上覆土层主要是全风化花岗岩，既有隧道亦位于全风化花岗岩中。地下水平均埋深为2.93 m左右。

4.2 工程监测

新隧道的该段施工于2019年完成。为掌握地层沉降及既有隧道的安全状况，实时监测了土体深层位移，以动态优化施工参数。同时，沿隧道纵向间距10 m与横向间距6 m对盾构下穿施工段进行地表沉降监测，且对距隧道轴线6 m进行深层土体水平位移监测，监测频率为盾构到达前后30 m为2次/d；30～50 m为1次/d；50 m以外1次/周。监测布置见图6。

图6 监测点布置

依据CJJ/T 202—2013《城市轨道交通结构安全保护技术规范》、DBJ/T 15-120—2017广东省标准《城市轨道交通既有结构保护技术规范》和本工程实际情况，拟定的位移控制报警值如表2所示。

表2 监控报警值

4.3 地层损失率控制指标的确定

首先按照间隙参数法估算地层损失率。中铁装备盾构机盾尾间隙为140 mm。不考虑开挖应力释放引起的土体变形以及人为因素引起的地层损失。考虑该工程的盾尾注浆效果，取系数为13%，则Gp=140×13%=18.2 mm。

将Gp代入式(17)，按照式(16)，计算得单位长度地层损失为Vl=0.25 m3。再将Vl代入式(1)得到单位长度地层损失率η=0.41%。

间隙参数法反映不了地层特性以及施工技术等的影响。为此，再参考表1的经验值。广州地区的地层损失率范围值为0.20%～3.14%，均值为1.07%。本工程地层条件较好，隧道上覆土层主要是全风化花岗岩。全风化花岗岩是一种特殊土，正常情况下强度较高，但如果大量失水、吸水或受到强烈震动，则强度会降低而发生一定的变形。综合间隙参数法的估算结果以及经验值，预估地层损失率在0.42%～0.65%之间。

为控制地层沉降，施工中地层损失率指标取为η=0.65%。

此外，需注意的是，如果不进行盾尾注浆，则Gp=140mm，算得η=3.16%，高于表1所示广州地区地层损失率经验范围值的最大值，对于地层沉降控制极为不利，这是不可接受的。

4.4 出渣量的控制

以盾构开挖过程中出渣量的控制来间接控制地层损失，并以此调配施工参数。其方法如下：

衬砌外半径8.8 m，加上地层损失，盾构掘进单环按1.5 m进尺的理论出土量为：

V=3.14×4.252×1.0065=91.77 m3

掘进过程中渣土要改良成泥浆，需向掌子面加注泡沫剂、水等。本工程每推进1.5 m约加15 m3的泡沫剂和水，则渣土量为106.77 m3，是91.77 m3的1.16倍。此外，还需考虑到掘进后渣土自身松散变化。综合泡沫剂和水的体积以及渣土松散的影响，总的松散系数采用1.2，则每掘进1.5 m的渣土量为109.43 m3。

每掘进10 cm出渣量为7.30 m3，施工采用渣土箱为22 m3，每出一箱土对应进尺为301 mm，以此来控制盾构出渣量。

4.5 沉降控制效果分析

施工中，整理地面沉降监测数据，利用Peck公式反分析，得到实际的地层损失。如果地层沉降在报警值以内，则维持施工参数基本稳定。如果地层沉降值接近报警值，说明地层损失偏大，出渣偏多。此时，就需要调整施工参数和减少出渣量。

本工程在施工过程中地层沉降未达到报警值，出渣量控制良好。盾构机下穿完成后，YK1+040断面和ZK1+300断面实测的地表沉降如图7所示，YK1+040断面最大沉降为7.23 mm，ZK1+300断面最大沉降为7.01 mm，在表2的黄色报警值之内。按Peck公式进行拟合，得到YK1+040断面拟合优度为0.848，ZK1+300断面拟合优度为0.803，均大于0.75，说明Peck公式拟合效果好。拟合所得的沉降槽宽度系数i分别为17.53，19.44 m，最大沉降值Smax分别为6.78，7.01 mm，代入式(6)，得到地层损失率分别为0.53%及0.60%。该地层损失率与施工采用的地层损失率控制值0.65%基本一致，说明施工工艺和施工参数匹配是合适的，地层沉降控制良好，也说明本工程采取的以地层损失率指导施工的方法是可行的。

图7 监测断面实测数据的Peck公式拟合曲线

5 结 语

本文分析总结了地层损失的主要计算方法和地层损失范围的经验值。针对某盾构隧道工程，进行了地层损失预估分析，选取了合适的地层损失指标，并以出渣量的控制来实现地层损失的控制，最终实现了对地层沉降的有效控制。主要结论如下：

(1)施工前，可依据间隙参数法、经验值表估算地层损失率，结合地面沉降控制要求，拟定合适的地层损失率控制指标。通过控制渣土出土量与掘进进尺的对应关系来实现对地层损失率的控制。

(2)施工中，需利用地层位移监测数据反算实际的地层损失率，与采用的地层损失率控制指标比较，可进一步调整地层损失率和渣土出土量，并优化调配盾构掘进参数，从而可较好控制地层沉降，防止出现过大沉降的风险。