基于稀疏贝叶斯学习的有砟轨道道砟层损伤识别

胡 琴, 陈 晗

(华中科技大学 土木与水利工程学院， 湖北 武汉 430074)

有砟轨道是中国铁路轨道体系的主要系统之一，由钢轨、扣件系统、轨枕、枕下道砟层和路基等部件构成[1]。枕下道砟层是有砟轨道系统的重要组成部分，其作用是将轨枕传来的压力均匀地传给路基，阻止轨枕的移动，缓和车轮对钢轨的冲击，使轨道系统具有足够的弹性。然而道砟层是有砟轨道系统中最脆弱、也是劣化最明显的结构层[2]。若道砟层损伤未被及时修复，会影响支承轨枕的刚度，引起轨道几何形状的变化，增加列车脱轨的风险[3]。

目前，针对有砟轨道枕下道砟层的损伤识别方法较少。人工目视检查是工程领域最常用且最简便的检测方法之一，但该方法只能有效检测出有砟轨道表面的损伤，而位于轨枕下的道砟层损伤很难通过肉眼观察。岩心贯入试验需要先获得岩心样本，然后在实验室进行测试，通过比较损伤和未损伤道砟的摩擦比，进而确定道砟层的损伤状况[4]，这种方法耗时耗力，且会破坏道砟的性能，影响列车的运行，难以大范围使用。探地雷达法作为一种安全、无破坏性的方法，通过在给定的频率范围内发射和接收电磁波，可以用于道砟层的损伤检测[5]，但该方法难以准确地定位损伤位置以及选取合适的频率范围[6]。因此，在不影响道砟层性能和使用的前提下，研究出一种能够准确定位和定量枕下道砟层损伤的方法，具有重大的工程意义。

基于振动数据的结构损伤识别方法已经广泛应用于土木工程领域[7]。由于结构的模态参数(如固有频率和模态振型)与其物理特性(如刚度、质量和阻尼)直接相关，如果假定结构发生损伤时，质量和阻尼不发生变化，则其频率和振型的变化可以作为结构刚度降低(结构损伤)的指标[8]。基于试验振动数据，使用模型修正方法“反算”结构刚度的分布，是土木工程中典型的逆问题，而逆问题的求解往往伴随着由模型误差和测量噪声导致的参数不确定性问题[9,10]。采用贝叶斯理论计算修正参数的最优解，并从他们的联合概率分布中评估参数的不确定性水平[11,12]，可以在一定程度上缓解结构损伤识别过程中存在的病态性。Lam等[13,14]在基于贝叶斯模型修正的有砟轨道道砟层损伤识别研究方面做了开创性的工作，通过计算模型参数的后验概率密度分布来获得最可能模型的修正值从而进行损伤识别，该方法在进行损伤识别过程中需要以无损状况下的道砟层刚度分布为基准线/参照线，而在实际应用中，无损状态下的基准线比较难获取。Huang等[15]对贝叶斯理论在结构损伤识别和评估方面的最新研究进展进行了全面综述。在实际应用中，结构损伤往往只出现在结构的少数单元，与结构的所有单元相比，损伤单元在空间上是稀疏分布的。基于这种先验条件，Huang等[16,17]提出了多层次稀疏贝叶斯学习方法来推断结构损伤位置和损伤程度，稀疏贝叶斯学习方法可以在迭代优化的过程中自动促进损伤参数的稀疏性，有效降低损伤识别误判的可能性。Hou等[18]简化了多层次稀疏贝叶斯学习方法中表征参数精度的超参数个数，提出了基于 EM (Expectation-Maximization)算法和Laplace近似[19]的稀疏贝叶斯学习方法，并用悬臂梁和平面框架试验验证了算法的有效性，该方法的超参数个数较少，且有实际的物理意义，提高了模型修正和损伤识别的效率。

本文建立了包含钢轨 - 轨枕 - 道砟层的二维有砟轨道模型，通过室内两跨三层异型框架结构损伤试验和有砟轨道室内试验的损伤工况试验数据验证了所提出的基于稀疏贝叶斯学习的道砟层损伤识别方法的有效性。

1 有砟轨道有限元模型

有砟轨道的三个主要构件是钢轨、轨枕以及枕下道砟层，如图1所示，钢轨承受列车的垂向荷载和横向荷载，并将其传递给轨枕，轨枕的主要作用是支撑钢轨并将钢轨传来的各项压力传递给道砟层，道砟层再将轨枕传下来的压力均匀地传给路基，阻止轨枕的移动，减缓和吸收轮轨的冲击和振动，使轨道系统具有足够的弹性。

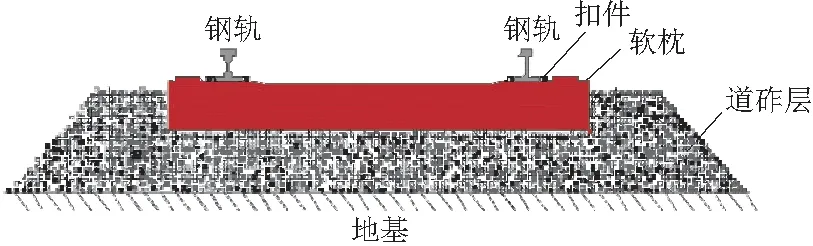
图1 有砟轨道结构示意

图2 二维有砟轨道模型示意

本文采用MATLAB建立了一个包含钢轨 - 轨枕 - 道砟层的二维有砟轨道模型[13]。其中，将枕下道砟层模拟为等效刚度为k的弹性地基，轨枕用弹性地基上的Timoshenko梁模拟，两根钢轨模拟为梁上对应位置的附加质量块，如图2所示。为得到道砟层刚度的分布，将枕下道砟层沿着轨枕的纵向平均分成n个区域[20]，第i区域道砟刚度的大小则为ki=cikb(i=1,2,…,n)，其中，kb为道砟层各区域等效刚度的标称值，ci为各区域道砟刚度的比例系数。

理论上，当枕下道砟层不发生损伤时，其支承刚度基本不变；当枕下道砟层发生损伤时，轨枕下一定区域内的支承刚度ki会减小，通过反问题求解出道砟层刚度变化量，就可识别出道砟层损伤。

由于轨枕横截面沿轨枕纵向为变截面，为了较准确描述轨枕横截面积大小沿轨枕纵向的变化，将轨枕等分为48个单元，忽略其轴向荷载和变形，考虑剪切变形对轨枕振动模态的影响，将轨枕模拟为Timoshenko梁，两根钢轨模拟为轨枕上的附加质量块。在本文中，有砟轨道模型的各项参数如表1所示。

表1 有砟轨道模型的各项参数[13]

2 稀疏贝叶斯学习理论

稀疏贝叶斯学习理论考虑了损伤总是发生在少数区域这一先验信息[16]，通过赋予一个用来描述损伤参数不确定性的超参数来约束逆问题的求解。在迭代求解过程中，对于未发生损伤的区域，其损伤参数的超参数会逐渐趋近于无穷大，说明该区域损伤的概率逐渐趋近于无穷小，相应的损伤参数逐渐趋近于0，即将无损的区域识别出来，从而增加了逆问题求解的条件，加快了算法收敛的速度，最终得到全局最优的收敛解。

2.1 基于EM算法的稀疏贝叶斯学习方法

当结构发生损伤后，其刚度会发生退化，其中第i个单元的损伤参数θi为：

(1)

损伤后结构的固有频率ω和模态振型φ包含了损伤的信息，稀疏贝叶斯学习理论是基于结构固有频率和模态振型在损伤前后的变化来识别道砟层的损伤位置和损伤程度。

根据贝叶斯理论，损伤参数的后验概率密度函数为：

p(θ|ω2,φ)=c-1p(ω2,φ|θ)p(θ)

(2)

式中：p(θ)为损伤参数的先验分布；p(ω2,φ|θ)为模态数据的似然函数；c-1为归一化常数。

基于概率公理，参考文献[18]，可得损伤参数的后验概率密度函数的表达式：

(3)

由式(3)可知，损伤参数θ的后验概率密度函数依赖于超参数{α,β,γ}的估计。采用EM算法最大化证据函数的自然对数的期望，得到超参数{α,β,γ}的表达式为：

(4)

(5)

(6)

由于无法得到损伤参数θ后验分布的解析表达式，采用Laplace近似方法，假定其为高斯分布，式(3)中损伤参数θ的最大后验估计值可以通过最小化后验概率密度函数的负对数求得，即等价于最小化目标函数J(θ)：

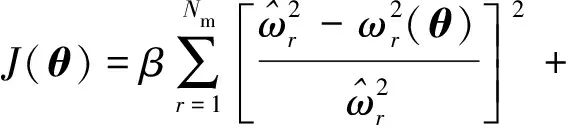
(7)

在优化目标函数J(θ)的过程中，当超参数αi趋近于无穷大时，相应的θi会趋近于0，从而得到稀疏的识别结果；超参数β和γ控制着频率和振型数据的参与程度，影响识别结果的精度。

(8)

2.2 基于稀疏贝叶斯学习的道砟层损伤识别方法

将有砟轨道模型中的枕下道砟层沿轨枕纵向分为n个区域[20]，假设除道砟刚度外，有砟轨道模型其余的各项参数均与有砟轨道在无损状态下的各项参数一致。

对道砟刚度损伤参数θ进行识别的具体步骤如下：

Step1：以测量得到的有砟轨道的频率和振型作为目标数据，同时对道砟刚度的损伤参数θ和超参数α，β，γ进行初始化，得到θ(0)，α(0)，β(0)，γ(0)。

Step 2：在第t(t≥1)次迭代过程中，采用EM算法不断修正模型的超参数和道砟刚度的损伤参数，具体如下：

从模型来看，地方感的3个维度之间呈显著正相关，具有较强的相互影响，且对身份认同与融合的作用存在差异。地方依恋和地方认同对身份认同与融合的直接贡献为正，而地方满意度对身份认同与融合的直接影响为负。

(9)

式中：Tol表示收敛准则，本文中Tol的值为10-4。

随着损伤参数数目的增加，需要的迭代次数t也会逐渐增多，若测量数据充足，则可以保证识别结果具有较高的精度。

3 实验验证

3.1 异型钢框架结构实验验证

首先本文采用如图3所示的实验室两跨三层异型钢框架来验证稀疏贝叶斯学习识别结构损伤的有效性，其中框架结构通过一块钢板固定在地面上，因此，可以将框架底部视为固定约束。框架结构的尺寸如图3所示。其中，梁和柱(除了单元4)的截面面积均为80.0×6.0 mm2，钢材的杨氏模量为2.0×1011N/m2，密度为7.70×103kg/m3。在本次试验研究中，将单根梁和柱当作一个欧拉伯努利梁单元，共计13个单元，每个单元长度为0.5 m。

图3 实验框架结构示意/mm

第4个单元宽度为60 mm，其他材料属性与框架结构其他构件一致，单元截面惯性矩的减小等价于结构单元的损伤，即第4个单元的损伤程度为25%。柱上每250 mm布置一个测点，梁上不布置测点，总共16个测点，用力锤水平敲击框架结构，传感器记录各测点的水平加速度，采用模态识别方法提取框架结构前4阶固有频率和模态振型。

采用稀疏贝叶斯学习迭代识别框架结构的损伤结果如图4所示。框架结构的前4阶固有频率的测量值、修正值以及振型的模态置信度准则值MAC值如表2所示，损伤工况下损伤参数的后验概率分布如图5所示。

图4 框架结构迭代过程中的损伤识别结果

由图4可得，经过2次迭代，结果收敛，能够较为准确识别出结构的损伤，识别结果为单元4损伤25.6%，识别误差为2.4%。由表2可知，框架结构实测固有频率与识别出的固有频率吻合较好，最大识别误差为第2阶频率的1.94%，且前4阶振型的MAC值均大于0.99，模态振型匹配良好。由图5可知，损伤参数识别结果的区间在0.2～0.3之间，损伤程度接近25%。综上可知，本文所提方法可以准确识别框架结构损伤。

表2 损伤工况的前4阶固有频率

图5 损伤工况下损伤参数的后验概率分布

3.2 有砟轨道结构实验验证

本文以文献[14]的实验损伤工况测量模态数据来验证所提方法的有效性，实验室模型中道砟层分成三个区域，从左到右的损伤参数分别为θ1，θ2，θ3；轨枕弹性模量的修正比例因子为θE，左右钢轨的质量修正比例因子分别为θL和θR。工况S1是在道砟层中间区域设置损伤，工况S2是在道砟层的左侧和中间两个区域分别设置损伤。采用文献[14]有砟轨道两种损伤工况下测量得到的频率和振型以及两种损伤工况下的轨枕和左右钢轨的修正参数(表3)，识别道砟层的刚度损伤参数的最大后验估计值，其结果如表4所示。

表3 两种试验损伤工况下的参数修正值

表4 两种试验损伤工况下道砟层的最大后验估计值

两种实验损伤工况下有砟轨道的前四阶固有频率的测量值[14]、修正值以及振型的MAC值如表5所示，两种损伤工况下损伤参数的后验概率分布如图6所示。

图6 两种试验损伤工况下损伤参数的后验概率分布

第一种损伤工况S1下，由表4可知，中间区域道砟刚度损伤了99%，左右两侧区域的道砟刚度接近无损状态，识别出的道砟刚度分布和试验预设的一致，表明所提出的基于稀疏贝叶斯学习的道砟层损伤识别方法可以准确识别出道砟层损伤。由表5可知，实测固有频率与识别出的固有频率吻合较好，最大识别误差为第3阶频率的3.82%，其次为第1阶频率的3.38%，其余2阶频率的识别误差均小于1%；前4阶振型的MAC值均大于0.99，匹配度较好。由图6a的损伤参数后验概率分布陡峭可知，损伤参数识别结果的不确定性较小。

表5 两种试验损伤工况下有砟轨道的前4阶固有频率

第二种损伤工况S2下，由表4可知，左侧和中间区域道砟刚度分别降低了34%，51%，右侧区域的道砟刚度未发生变化，识别出的道砟刚度分布和试验预设情况一致。由表5可知，实测固有频率与识别出的固有频率吻合较好，最大识别误差为第4阶频率的3.40%，其余3阶频率的识别误差均小于1%；前3阶振型的MAC值均大于0.98，匹配度较好。由图6b损伤参数的后验概率分布可知，左侧区域损伤参数的不确定度较小，中间区域损伤参数的不确定度相较左侧区域较高，两者的不确定度都在可接受范围内。

4 结 论

本研究提出了一种基于稀疏贝叶斯学习的有砟轨道枕下道砟层损伤识别方法，该方法利用有砟轨道系统的模态数据，使用基于EM迭代算法的稀疏贝叶斯学习方法对有砟轨道的有限元模型进行修正，计算道砟层的刚度损伤参数，从而对道砟层损伤进行定位和定量识别。相关结论如下：

(1)道砟层损伤实验结果表明，采用稀疏贝叶斯学习方法能够识别相应的道砟层刚度损伤参数，成功定位和定量识别道砟层的损伤。

(2)稀疏贝叶斯学习通过最大化证据函数来处理超参数的优化，促进了道砟层刚度损伤识别结果的稀疏性，加快了算法收敛的速度。

(3)与确定性损伤识别方法相比，稀疏贝叶斯学习可以计算损伤参数的后验概率分布，从而定量描述损伤识别结果的不确定度。有望为道砟层的损伤检测及维修养护提供一定的技术保障。