泡沫混合土中颗粒间黏结强度理论计算方法

刘正日，王树英,2，王海波，钟嘉政，瞿同明

(1. 中南大学土木工程学院，湖南长沙，410075；2. 重载铁路工程结构教育部重点实验室，中南大学，湖南长沙，410075；3. 斯旺西大学辛克维奇工程计算中心，英国斯旺西，SA1 8EP)

盾构在砂性土地层中施工时，常采用改良剂提高渣土的塑流性以保证其能够顺利掘进，其中，泡沫是最典型的改良剂。砂性土是颗粒性明显的散体材料，与泡沫混合后形成具有一定塑性的黏聚体[1-4]。泡沫改良砂性土宏观性质的变化是由其细观尺度上接触力学关系改变引起的，研究者大多采用能进行细观尺度分析的离散元数值模拟方法对其进行研究[5-6]。离散元方法可有效表征砂土孔隙压力特征[7]，通过观察试样内部颗粒运动状态，可解析砂土受剪破坏时其剪切带形成的微观机制[8]，能够较好地应用于散体材料模拟，解释相关过程的力学机理[9-10]。就泡沫改良砂土而言，加入泡沫后，土体中的细观接触关系由单一的砂土-砂土颗粒间接触转变为砂土-砂土、砂土-泡沫、泡沫-泡沫这3 种颗粒间接触共存。为实现泡沫改良土的精细化模拟，需选择合适的本构模型及对应细观参数来反映这3 种接触关系。其中，砂土-砂土颗粒间的接触力学行为主要是线弹性行为，可选择线性接触模型作为其本构模型[11]。相对而言，泡沫-泡沫及砂土-泡沫颗粒间存在一定的黏结力，因此，需选择可体现颗粒间黏结作用的平行黏结模型[12]。泡沫颗粒的引入使土体中出现黏结力，从而改变了砂土的塑流特性，因而，合理确定颗粒间的黏结强度参数对模型准确反映泡沫改良土的真实特性有至关重要的作用。

反演法是应用最广泛的参数确定方法[13]，但此方法需要耗费大量的计算时间[14]。为提高参数标定效率，RACKL 等[15]基于拉丁超立方体抽样和克里格法提出了一种颗粒材料的标定方法，有效减少了离散元细观参数标定时间。FALKE 等[16]建立了一套仅靠简单环剪试验结果便可自动确定离散元细观参数的程序，所提出的参数化方法能够较好地对模型参数进行实验识别，从而不需对数值参数进行调整。YE等[17]采用BP神经网络建立了离散元细观参数与颗粒宏观特性间的非线性关系，通过训练后可高效、精确地确定离散元模型参数。QU等[18]通过推导颗粒系统宏观参数与细观参数间的解析关系得到模型线性接触刚度的近似值，再结合梯度下降算法获得较可靠的估计值。CHENG等[19]提出了考虑细观参数耦合作用的标定程序来确定砂土的细观参数。尽管上述方法都可用于标定模型细观参数，但其结果没有直接的物理基础[20]。

当前，对于盾构砂性渣土改良，多基于常压条件下进行坍落度试验来确定盾构掘进过程中渣土改良参数[21]，本文作者对常压条件下泡沫改良土中砂土-泡沫颗粒及泡沫-泡沫颗粒间的黏结作用进行研究。基于颗粒力学角度，推导颗粒间抗拉强度的理论计算式，并采用颗粒间抗拉强度测定装置探究泡沫溶液质量分数及泡沫颗粒半径对泡沫-泡沫及砂土-泡沫颗粒间抗拉强度的影响规律，最后，依据试验结果验证理论公式的可靠性。

1 颗粒间黏结强度理论计算

1.1 泡沫-泡沫颗粒间黏结强度解析式

为确定泡沫混合土中颗粒间黏结强度这一关键细观参数，对泡沫-泡沫及砂土-泡沫颗粒间的黏结破坏过程进行分析，从而推导出颗粒间黏结强度的理论解析式。图1所示为泡沫分离过程的示意图及几何关系，其中，图1(a)所示为两泡沫颗粒分离状态，图1(b)所示为两泡沫颗粒接触状态，图1(c)和图1(d)所示为接触状态下两泡沫颗粒几何关系。

考虑到试验在常温、常压条件下进行，假设试验过程中大气压强和温度保持不变。由于两泡沫颗粒在接触及分离过程中仅接触界面相融合，接触面之外泡沫仍保持球形曲面形态，根据理想气体状态方程，可知两泡沫颗粒在接触融合与分离过程中其体积保持不变，其相关几何参数为

式中：V1，R1和S1分别为非接触下单个泡沫颗粒的体积、半径及表面积。

根据图1(d)几何关系可得：

式中：R2为接触状态下泡沫颗粒的半径；R3为两颗粒接触界面半径；H为接触状态下泡沫颗粒中心至接触界面的距离。

泡沫-泡沫颗粒分离过程中单个泡沫颗粒体积不变，故

接触泡沫分离后单个泡沫颗粒增加面积S增为

两泡沫接触时由一层公共界面分隔，当两泡沫分离后,公共界面分离为2 个单独界面，因而，泡沫液膜生成新表面，其所需外界提供的能量E1为

式中：γ为溶液表面张力；S增1为分离后单个泡沫表面积增量。

由于泡沫颗粒发生形变后，能恢复原来的大小和形状，可视为弹性体[22]，颗粒间分离过程中可视其发生弹性变形，因此，可得两泡沫颗粒形心发生位移所需的作用力F1与相对位移s1的关系式为

式中：k1为泡沫颗粒变形刚度。

泡沫颗粒分离过程中外力对泡沫系统所做的功为

式中：E1为泡沫颗粒分离所需的能量；W位移1为两泡沫颗粒分离过程中形心总相对位移。

根据能量守恒定理，联立式(7)和式(8)可得

则泡沫颗粒间抗拉强度σ1为

式中：F极限1为颗粒间分离力；S界面1为颗粒间接触界面面积。

1.2 砂土-泡沫颗粒间黏结键强度解析式

砂土-泡沫颗粒间分离过程与泡沫-泡沫颗粒间的分离过程类似。图2 所示为单个砂土-泡沫颗粒在分离过程中的示意图。

由于泡沫颗粒在与砂土颗粒接触及分离过程中保持完整，且试验过程中外界压强及温度不变，因此，根据理想气体状态方程，可假设泡沫颗粒与砂土颗粒在接触融合与分离过程中体积变化忽略不计。

由于泡沫颗粒与砂土颗粒接触前后体积不变，故接触前后泡沫颗粒半径关系为

式中：R4为泡沫-砂土颗粒非接触状态泡沫颗粒半径；R5为接触状态下泡沫颗粒半径。

砂土和泡沫接触后，泡沫颗粒呈半球体，因此，接触泡沫分离后单个泡沫颗粒增加面积S增2为

当砂土-泡沫分离后，泡沫液膜生成新表面，其所需外界提供的能量为

式中：E2为泡沫与砂土颗粒分离所需提供的能量；S增2为分离后泡沫颗粒表面积增量。

泡沫颗粒可视为弹性体，颗粒间分离过程中可视其发生弹性变形，因此，可得泡沫与砂土颗粒分离所需的作用力F2与相对位移s2的关系式为

式中：k2为颗粒变形刚度。

泡沫与砂土颗粒分离过程中外力对系统所做的功为

式中：W位移2为泡沫-砂土颗粒分离过程中两颗粒形心的总相对位移。

根据能量守恒定理，联立式(13)和式(15)可得

则砂土-泡沫颗粒间抗拉强度σ2为

式中：F极限2为泡沫-砂土颗粒间分离力；S界面2为泡沫-砂土颗粒间接触界面面积。

综上可知，在泡沫改良土的离散元数值模型中，只需测得泡沫的表面张力及确定模型中泡沫颗粒粒径，便可根据式(10)及(17)确定泡沫-泡沫颗粒及砂土-泡沫颗粒间的黏结强度。为验证该解析式的可靠性，采用颗粒间抗拉强度测定装置测定泡沫-泡沫颗粒及砂土-泡沫颗粒间的抗拉强度，并探究泡沫溶液质量分数及泡沫颗粒半径对泡沫-泡沫及泡沫-砂土颗粒间抗拉拔强度的影响规律。

2 试验方案

2.1 试验材料

砂土地层盾构掘进常采用通用型泡沫剂作为改良剂，试验选择以该类型泡沫剂为溶质的泡沫溶液作为泡沫发生试剂，其主要成分为阳离子表面活性剂十二烷基三甲基氯化铵、复配有阴离子表面活性剂十二烷基硫酸钠以及非离子表面活性剂氯代十二烷等，属于阴阳离子复配型泡沫剂。

2.2 试验设备

为了测定泡沫-泡沫、砂土-泡沫颗粒间抗拉强度，设计颗粒间抗拉强度测定装置，如图3 所示，装置由精度为0.001 g 的高精度电子秤(a)、升降支架(b)、上部泡沫固定管(c)、下部泡沫(土颗粒)固定管(d)组成。上部泡沫固定管(c)垂直固定于升降支架的伸臂上，可通过调节旋钮随伸臂上下运动；下部泡沫固定管(d)垂直固定于铁垫片之上并将其整体放置于电子秤中部。

2.3 试验方案

2.3.1 颗粒间抗拉强度测定

泡沫颗粒接触状态及分离状态图片如图4 所示。测定泡沫-泡沫、砂土-泡沫颗粒间抗拉强度的具体试验步骤如下。

1)配制特定质量分数的泡沫溶液。泡沫溶液质量分数为泡沫剂在泡沫溶液中的质量占比。

2)根据被测泡沫粒径选择合适管径的泡沫固定管垂直固定于升降支架的伸臂之上，将另一泡沫固定管垂直固定于铁垫片上，使固定管中心轴与垫片平面保持垂直。然后，将垫片连同固定管放置于电子秤上。试验时，两泡沫固定管的竖向中心轴线保持重合。

3)往注射器中吸入与目标泡沫颗粒体积相同的气体，尖端蘸取适量的泡沫溶液，生成具有目标体积的泡沫颗粒。将泡沫颗粒导引至上部泡沫固定管下端。当测定泡沫-泡沫颗粒间抗拉强度时，将泡沫颗粒导引至下部泡沫固定管上端；当测定砂土-泡沫颗粒间抗拉强度时，将砂土颗粒置于下部固定管上端。

4)对电子秤的质量读数清零，旋转升降支架旋钮使2个泡沫(或泡沫与砂土颗粒)相互接触并在接触面处融合，之后适当旋转旋钮使电子秤读数为0。

5)拍摄记录泡沫接触且电子秤读数为零时的图片，用于后期获得两颗粒间接触面的直径(图4(a))。

6)将升降支架匀速缓慢向上运动，使上部泡沫固定管随伸臂缓慢升高直至2个颗粒相互分离并拍照(图4(b))，电子秤自动记录2 个泡沫颗粒分离过程中的峰值读数，此即为使泡沫-泡沫(或砂土-泡沫)颗粒分离所需的拉力。

泡沫-泡沫(或砂土-泡沫)颗粒间的抗拉强度σ为两泡沫颗粒间分离时所能承受的拉力F极限与颗粒间接触界面面积S界面的比值，其计算式为

在颗粒接触过程中，假定体积不变而且近似球形。

2.3.2 溶液表面张力测定

泡沫溶液表面张力采用JZHY-180型表面张力仪测量(见图5)，具体测量步骤为：将铂金环装在吊杆臂上，把被测溶液倒在玻璃杯中，液面高为20～25 mm，将此玻璃杯放在样品座A 的中心位置，旋转底端螺母B，玻璃杯便与样品座A一起上升，使铂金环浸入溶液中，且使臂上的指针与镜片上的红线重合；旋转蜗轮手柄C 增加钢丝的扭力，当液体表面被铂金环拉得很紧时，指针L始终保持与红线相重合。继续施加这2个力，直到液体薄膜破裂，刻度盘上指针的读数就是被测液体的表面张力。

2.4 试验工况

泡沫液膜的性质主要由排列在界面的表面活性剂分子决定。当泡沫溶液质量分数提高时，分布在液膜界面上的表面活性剂分子数量随之增加[23]，使得溶液表面张力相应减小。因此，泡沫溶液质量分数变化改变了溶液表面张力，进而对泡沫的力学性质产生较明显影响。此外，由于试验过程中存在测量误差，当泡沫颗粒粒径较小时，测量误差对试验结果影响会更大。另外，根据式(10)和式(17)，颗粒间抗拉强度与粒径之间存在一定联系，因此，可在试验中放大颗粒粒径并根据试验结果拟合得到粒径与作用力之间的关系式，从而得到全粒径范围内颗粒间作用力。试验中，通过生成不同体积的泡沫颗粒得到对应的颗粒粒径，最小泡沫颗粒体积为0.5 cm3，最大泡沫颗粒体积为3 cm3，以0.5 cm3的增量逐次递增，对应泡沫颗粒半径范围为0.49～0.89 cm，并且分别配置质量分数为1%，3%和5%的泡沫溶液进行试验。对每种粒径工况进行5组重复性试验，取平均值作为试验结果。

为探究泡沫溶液质量分数及泡沫粒径对泡沫-泡沫、砂土-泡沫颗粒间作用力的影响，试验工况分别如表1和表2所示。

表1 泡沫-泡沫颗粒间抗拉强度试验工况Table 1 Test conditions of tensile strength between foam and foam particles

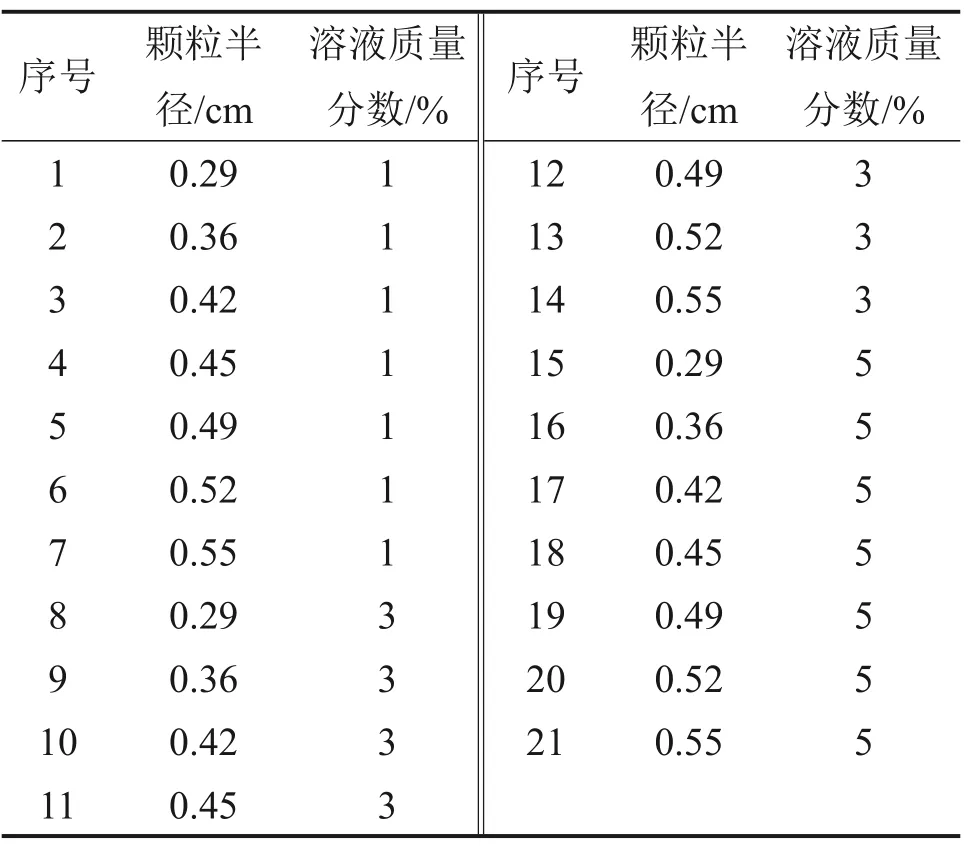
表2 砂土-泡沫颗粒间抗拉强度试验工况Table 2 Test conditions of tensile strength between sand and foam particles

3 试验结果及分析

3.1 泡沫-泡沫颗粒间接触力学特性

3.1.1 泡沫粒径对泡沫颗粒间接触界面半径的影响

图6所示为两等粒径泡沫颗粒间接触面半径与泡沫颗粒半径间的关系，可以得到泡沫颗粒间接触界面半径与颗粒半径间大致呈斜率为0.842的线性关系。由此可知，两等粒径泡沫颗粒在不受外力的条件下接触，颗粒接触界面与单个泡沫颗粒半径的比值为定值。由此可得两泡沫颗粒接触界面半径仅与泡沫颗粒本身粒径相关，在实际应用时，只需测得泡沫颗粒的粒径便可通过对应关系得到两泡沫颗粒相接触时的接触界面半径。

3.1.2 泡沫粒径对泡沫颗粒间分离拉力的影响

图7所示为泡沫颗粒间分离拉力与颗粒半径间的关系曲线。从图7可知：等粒径泡沫颗粒间的分离拉力随泡沫颗粒半径增加而增加，两者之间大体上呈线性关系。根据泡沫颗粒间接触面半径及泡沫颗粒间分离拉力与泡沫粒径间的关系曲线(图6和图7)，可得泡沫颗粒间抗拉强度与颗粒半径间的关系曲线如图8所示。根据图8可知：泡沫颗粒间的抗拉强度与泡沫颗粒半径大体上呈反比例关系；随着泡沫颗粒半径增加，泡沫颗粒间的抗拉强度随之减小。出现这一现象的原因是两泡沫颗粒在接触界面处融合后，泡沫液膜表面气-液界面张力转变为液体本身液-液界面张力，泡沫颗粒间所能承受的拉力绝大部分由沿泡沫颗粒间接触界面分布的气-液界面张力承担，泡沫颗粒间整体所能承受的主要拉力随颗粒界面半径呈一次方的线性关系增加，而泡沫颗粒间接触界面面积与界面半径的二次方呈正相关关系；当泡沫颗粒半径增加时，颗粒间界面面积的增长量为半径的2 次方，拉力增长量为半径的1次方，因此，泡沫颗粒间抗拉强度与颗粒半径呈反比例关系。

3.1.3 泡沫溶液质量分数对泡沫颗粒间抗拉强度的影响

图9所示为泡沫颗粒间抗拉强度与泡沫剂溶液质量分数间的关系。从图9可见：随泡沫溶液质量分数增加，泡沫颗粒间抗拉强度有所减小。这是由于泡沫溶液质量分数增高可使溶液中表面活性剂分子数量增加，使得泡沫颗粒气-液界面间的表面活性剂分子数量增加，从而有效减小泡沫颗粒气-液界面间的张力，而泡沫颗粒间所能承受的拉力主要由颗粒气-液界面间的张力提供，所以，增大泡沫溶液质量分数会使泡沫颗粒间的抗拉强度减小。泡沫溶液质量分数与表面张力间的关系如图10所示。从图10中不同溶液质量分数下泡沫溶液的表面张力曲线可知[23]，初始添加表面活性剂时，表面活性剂分子分布在溶液表面使其表面张力急剧减小，然而，溶液表面所能填充的表面活性剂分子数量有限，当泡沫溶液质量分数从1%增至5%时，排布于溶液表面的表面活性剂分子数量略有增加[24]，因此，溶液表面张力仅较小下降，这与增大泡沫溶液质量分数后泡沫颗粒间的抗拉强度略微减小相符。

此外，泡沫颗粒粒径越大，泡沫溶液质量分数对其抗拉强度的影响越小。这是由于颗粒间的抗拉强度与溶液表面张力成正比，与颗粒间半径成反比，当泡沫溶液质量分数增加时，较小粒径的泡沫颗粒黏结强度下降更大。

3.2 砂土-泡沫颗粒间接触力学特性

3.2.1 泡沫颗粒粒径对砂土-泡沫颗粒间接触界面半径的影响

图11所示为砂土-泡沫颗粒间接触界面半径与泡沫颗粒半径间的关系。从图11 可知：随泡沫颗粒半径增加，颗粒间接触界面半径大致呈线性增加，其斜率约为1.32；当泡沫颗粒与砂土颗粒接触后，泡沫颗粒由于界面力的影响发生了明显变形。由于液膜在四周受到相等的气压作用，因此，其与空气接触的部分保持为球形，使得液膜整体为球体的一部分。考虑到在变形过程中，泡沫颗粒依然保持完整且外界大气压强及环境温度不发生变化，根据理想气体状态方程可得泡沫颗粒整体体积不变时，变形前与变形后泡沫颗粒的粒径比值为1.26，与试验结果较接近，表明试验结果较准确。

3.2.2 泡沫颗粒半径对砂土-泡沫颗粒间抗拉强度的影响

图12所示为砂土-泡沫颗粒间的抗拉强度与泡沫颗粒半径间的关系。从图12 可知：颗粒间抗拉强度随泡沫颗粒半径增加而减小，两者间大体上呈反比例关系。砂土-泡沫颗粒接触界面间黏结力主要由固-液界面张力及边界处固-液-气三相界面张力组成，颗粒间受拉时，泡沫-砂土颗粒间的抗拉强度也由这两部分提供。当泡沫颗粒半径增加时，边界处固-液-气三相界面张力随泡沫半径增加呈线性增大，接触面面积与颗粒半径的平方呈正比，固-液-气三相界面张力对界面张力的贡献与泡沫颗粒半径呈反比例关系。固-液界面张力对抗拉强度的贡献部分不发生变化，因此，砂土-泡沫颗粒间的抗拉强度随泡沫颗粒半径增加而减小，并且当半径增大到一定程度时，强度受半径的影响程度逐渐减弱。

3.2.3 泡沫溶液质量分数对砂土-泡沫颗粒间抗拉强度的影响

为分析泡沫溶液质量分数对砂土-泡沫颗粒间抗拉强度的影响规律，对质量分数为1%，3%和5%这3 种泡沫溶液砂泡间抗拉强度进行测定，试验结果如图13 所示，从图13 可见：砂土-泡沫颗粒间抗拉强度随泡沫溶液质量分数增大而略有减小。由于泡沫溶液质量分数增加使得固-液界面及边界处固-液-气三相界面处表面活性剂分子数量增加，界面张力随之减小。而泡沫与砂土颗粒间的抗拉强度主要由界面张力产生，因此，砂土-泡沫颗粒间界面张力随泡沫溶液质量分数增加而减小。界面张力仅产生于泡沫与砂土颗粒接触界面的边界上，其与泡沫颗粒半径呈线性关系。随着泡沫溶液质量分数增加，界面张力随之减小，从而造成颗粒间抗拉强度减小。然而，由于抗拉强度与接触面面积呈反比例关系，在界面张力减小幅度相同的条件下，泡沫颗粒粒径越大，溶液质量分数对颗粒间抗拉强度的影响就越小。

4 颗粒间抗拉强度理论结果与试验结果对比

为了验证颗粒间抗拉强度解析式是否合理，对颗粒间抗拉强度的理论计算结果与试验结果进行对比，图14 和图15 所示分别为泡沫-泡沫和砂土-泡沫颗粒间抗拉强度对比，所用的泡沫剂质量分数为3%，与前面试验工况相吻合。从图14和图15 可见：除个别数据点外，颗粒间抗拉强度的理论值与实测值随泡沫颗粒半径的增大趋势一致，且两者相对误差不超过10%，因此，可以分别采用式(10)和式(17)计算泡沫-泡沫颗粒间和砂土-泡沫颗粒间的抗拉强度。造成两者差异的原因主要是基于能量守恒原理进行颗粒间抗拉强度计算时忽略了颗粒分离过程中的能量损耗，然而，实际上，颗粒分离过程中存在能量损失。

5 结论

1)基于能量守恒原理，推导了泡沫-泡沫及砂土-泡沫颗粒间抗拉强度与泡沫颗粒粒径及溶液表面张力相关的理论计算公式。

2)泡沫-泡沫、砂土-泡沫颗粒间的抗拉强度主要受泡沫颗粒半径及泡沫溶液质量分数的影响，颗粒间的抗拉强度随泡沫颗粒半径增加而明显减小；随泡沫溶液质量分数增加，颗粒间的抗拉强度有所减小。

3)泡沫溶液的表面张力主要受溶液质量分数影响，在一定质量分数范围内随溶液质量分数增加而减小。而颗粒间抗拉强度主要受泡沫液膜的表面张力影响，因此，泡沫溶液的质量分数对颗粒间抗拉强度有较明显影响，增加泡沫溶液质量分数可有效减小颗粒间抗拉强度。

4)颗粒间抗拉强度的理论值与实测值较吻合，采用理论计算式可较好反映颗粒间的抗拉强度。

5)需说明的是，本文试验仅测定了等粒径泡沫颗粒间的抗拉强度，未考虑不同粒径颗粒间的抗拉强度特性，结果有一定局限性，并且在推导抗拉强度理论式时，忽略了颗粒间化学键等内在因素对分离过程能量损耗的影响，使理论值与实测值存在一定差异。然而，在离散元数值模型中，受计算能力限制，常常在简化模型中采用等粒径颗粒表征泡沫，所以，获得的泡沫-泡沫及砂土-泡沫颗粒间的抗拉强度理论计算公式可较好应用于离散元数值模型。在已知模型中泡沫颗粒粒径及对应溶液表面张力时，通过理论公式可方便地确定泡沫改良砂性土离散元模型中黏结键强度参数，且该参数选取方式有物理依据，取值结果较合理，可为建立精细化泡沫改良砂土离散元数值模型提供参考依据。