卷烟运输车辆配载研究——以上海烟草卷烟配送中心车辆装载为例

□ 唐 颖,高倩芸,张文婷,陈晓健,陈 伟

(上海烟草集团有限责任公司上海烟草储运公司，上海 200439)

1 引言

随着物流设施和设备的革新，信息技术在物流中的广泛应用，烟草行业需要通过物流策略来提高工作效率，降低企业经营成本，优化核心业务流程，提升企业市场竞争力。从烟叶制成到卷烟，再从卷烟仓库销售到终端，其物流环节之多、控制之严是烟草行业物流的特点。国家专卖的管控、原料产地的限制使得烟草行业的物流研究具有独特的研究意义。车辆的配载和装车是物流的重要环节，直接影响物流成本，而上海烟草集团产销规模的扩大，客户对卷烟的需求朝着多样化、小批量、多频次和个性化方向发展，同时烟草物流业务的运营体量和复杂程度与日俱增，如何依据全国各地客户点订单情况，并结合物流线路、运输工具、货物(烟件)规格等若干因素，进行快速、有效的车辆配载及货物装车成了上烟物流业务中一个迫切需要解决的问题。

目前，上海烟草集团有限责任公司上海烟草储运公司(以下简称“储运公司”)的卷烟装车业务在单车配载优化环节，长期以来都是凭经验来给运输工具进行配载的，是否已经达到运输工具使用率的最大化、配载效益的最大化却无从评估，同时这种配载方式强烈依赖员工的个人能力和经验，不利于大规模推广。此外，在利用装卸工人的经验进行装车操作时，只考虑车辆空间利用率及载重利用率，不仅无法保障车辆行驶路程，还导致了人力、物力和财力等方面成本的增加。

综上，有必要对烟草物流的智慧配载与装车方法进行深入研究，根据实际业务需求，提出一种适用于烟草行业的配载与装车优化解决方案，从而提高车辆满载率和装车一次成功率。

国内对货运配载的相关研究大致分为两个方向，一个是考虑车辆数目的多少与载重、容积及往返距离的约束等建模的方法，模型的运算与设计以启发式算法为主，例如：FFF(Finite First-fit)、FBS(Finite Best-fit)、基于禁忌搜索的元启发式算法、自适应遗传算法等；另一个则是对传统货运配载路径的研究，主要是解决一维装箱问题，结合遗传算法的混合启发式算法的二维装箱问题，采用遗传算法解决不同包装类型的三维装箱问题等。关于烟草行业的研究大多集中在物流成本控制和配送路径优化方面，而针对烟草智慧配载与装车方法的相关研究较少。

2 问题描述与模型构建

卷烟的配载与装车实际上是一个三维装箱问题。三维装箱问题(Three-dimensional Bin Packing Problem,3D-BPP)即物体在三维空间的摆放优化问题，可以描述为具有长、宽、高的n个物体在一个车箱中摆放，在满足一定的约束条件下，使装箱利用率最高。通过模型来刻画装箱问题，解决 “如何用车”和“怎么装车”的优化问题，有效提高烟草运力、节约配载和装车时间、降低物流成本。

本研究通过对实际业务需求的调研，例如：统计花式烟种类、件烟规格及包装尺寸、车厢尺寸等基本数据以及订单物流信息等，准确界定研究问题，充分考虑各种烟草配载装车场景，建立符合实际业务需求的配载运输模型。确定优化目标与约束条件，建立车货匹配及装车运输模型。

2.1 模型假设

多尺寸货物(烟草)的运输车辆装箱优化问题是将待装货物为不同种规格的若干个矩形物体，按照一定的规律装入运输车厢中，使得车箱利用率最大。要求满足以下假设：

①所有车厢和货品形状为大小不同的长方体；

②所有货品质量分布均匀；

③所有货品的外包装具有足够的承重能力，不会由于堆积而变形；

④每个订单包括多种货品，订单信息包括货品种类、需求数量；

⑤每个订单不可拆分装车。

2.2 参数和变量

假设烟草装载配送中心有N辆不同型号的箱式货车，每辆货车的最大容积为V。货车车厢可抽象成一个长L、宽W、高H的三维长方体。客户i需要多种类货物p，设每个货物j的长宽高为(lj,wj,hj)。不妨设车厢和货物的长、宽、高在整数范围内取值。主要参数和变量定义如表1和表2所示。

2.3 目标函数及约束性条件

(1)

(2)

ujn=ukn,∀j,k∈Oip,∀n∈N,i∈I,p∈P

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

模型解释如下：目标函数(1)是装箱率最大即累加所有装到车箱里的货品的体积最大；约束(2)表示每个货品只能被装到一辆货车中；约束(3)限制订单中每个种类的货品需求只能由一辆货车完成，即订单中同一种类的货品不能被拆分运输；约束(4)确保每辆货车的每个车厢装载的所有货品的体积不超过该车厢的容量限制；约束(5)-(7)确保装入车厢的货品不能违反该车厢的长、宽、高限制；约束(8)-(10)表示货品的前左下角顶点与后右上角顶点之间的坐标关系；约束(11)-(14)确保同一车厢中的两个货品至少存在一种位置关系(左右、前后、上下)；约束(15)-(17)确保同一个车厢中的任意两个货品不重叠；约束(18)-(19)限制决策变量的取值范围。

3 启发式算法设计

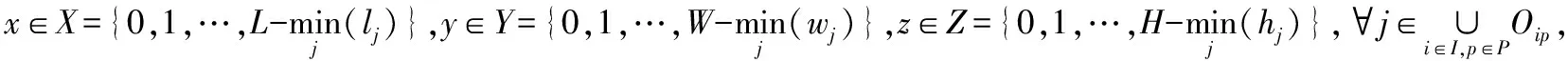
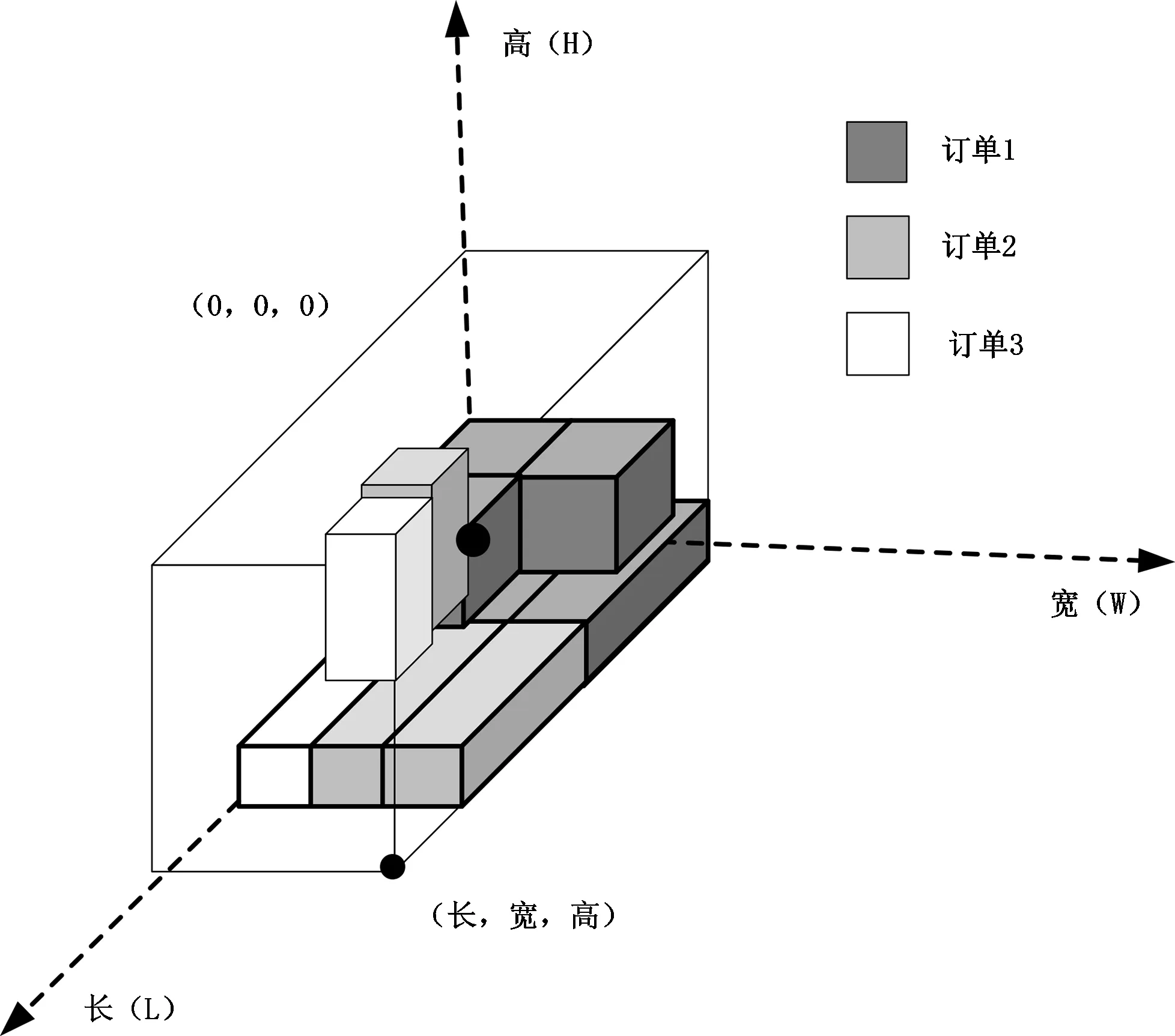
图1 不同货物的装箱示意图

多种不同尺寸的物品装箱问题是个NP-Hard 问题，通常采用启发式算法进行求解。本文根据烟草公司装箱的特殊需求和笛卡尔坐标的特点设计一种启发式求解算法，启发式算法遵循了货物一定是存在上下、前后、左右中的一种关系且货物不允许空放。基本思路如下：①根据烟草订单的目的地，设计每辆车的装箱方案；②确保订单不拆分的情况下所有种类的货物装箱并满足所有装箱约束；③订单里的所有货物都装箱完成后，判断装箱率，一般原则大于90%，则产生最优装箱方案，否则，重新安排装箱，如此循环。

算法1 启发式三维装箱步骤1从货物集合B和放置点集合items中取出需要的数据。步骤2 针对每一个货物,进行以下步骤:2.1 根据取出的货物bi(i∈1,…,n)的规格以及放置点的位置判断其在方向1的情况下能否装入车内。2.1.1若可以装入,则判断货物bi与其他货物是否发生重叠,2.1.1.1若发生重叠但是因为行间长度不一致导致的重叠则会根据行间约束规则生成新的放置点并存入集合,否则不对该放置点进行放置。2.1.1.2若没有发生重叠则判断货物bi是否悬空。2.1.2若不悬空并且bi的长度小于其底部货物的长度则在此放置点进行放置并生成新的放置点,再去除下一个放置点和货物,判断货物集合是否装完。否则按照相应的约束规则进行放置。2.2若方向1无法放置货物则判断方向2是否可以装入,若可以则判断相关的约束条件是否成立执行操作,否则判断方向3是否可以装入。步骤3 若三个方向都无法装入货物则该放置点不进行货物放置,取出下一个放置点。步骤4 当货物集合全部装完返回货物在车厢内的坐标和货物种类并存入output中。步骤5 配载验证系统根据output来绘制所需的装车图。

图2 算法流程图

4 数值实验与实证分析

本文采用上烟公司装箱的实际数值来验证模型。采用运行系统为Windows 10 X64，处理器为Intel(R) Core(TM) i7-10510U CPU@1.80GHz，内存为2.30 GHz。在运行环境中默认参数设置下，采用python 语言实现三维装箱问题的启发式算法。

4.1 参数设置

在实例中，运输车队选择经常使用的两款车型，货车车厢的规格数据如表3所示。根据订货的实际情况选取相关货品规格，如表4所示。

表3 车辆规格

表4 装载货物的基本信息

4.2 结果分析

算法以净装箱率为评价指标，实验结果如表5所示。

数据结果显示，每辆车根据订单的量进行组合，尽量满足90%以上的装箱率，如果要提高装箱率，可以对某些订单进行拆分处理。根据订单的要求，如果同一订单的货物不允许多个车厢运输的话，会出现降低装箱率的问题。因此，如果货物较多，可以选择车队的方式进行烟草货品运输。

车厢内可以放置的方式不一定按照订单的顺序，可以根据货物的尺寸决定哪单货物最先放置，前提是该车的货物卸货没有先后顺序。这与上烟的实际情况一致，一般同一辆车或者一个车队会去相同的目的地同时卸货。由于每类货物的需求量不同，不一定总能码垛成一个立方体，有些地方可能会空几箱货物。如果全码齐，则装箱率最高。如果订单可以拆分的话，不一定一个订单必须装在一辆车里，则可以全部码垛成立方体，提高装箱率。

现有的数据模拟结果显示，12.5米半挂巴士车至少可以容纳1050-1110箱货物，从而保证较高的装箱率。

5 结论

本文研究订单不拆分的多尺寸烟草三维装箱问题，充分考虑了多种类多货品的混装特点，构建了混合整数线性规划模型。同时提出了一种启发式算法，该算法考虑了多种实际约束，可以用最简单的方法，在最短的时间内得出近似最优解。实验结果表明，算法优化效果显著。

本文基于多尺寸烟草货品的装箱问题展开研究，未来可进一步结合运输路径及配送顺序等研究车辆路径问题。结合订单客户点的顺序，进一步深化研究考虑烟草在车场三维装箱的装箱顺序。

表5 车厢长宽高为11800*2300*2450的实验结果