数据驱动的服装物流分类及订货策略研究*
□ 袁 媛,高 波
(太原科技大学 交通与物流学院,山西 太原 030024)
更好、更有效、更经济地进行库存管理是解决服装企业问题的最佳方法,但许多服装专卖店的库存管理只是依据经验进行,缺乏一定的科学性,因而需要改进。
西方学术界对库存管理的研究起步较早,研究范围涉及的领域宽泛。Taleizadeh等[1]将EOQ模型和预付购买模型进行结合,构建了两者的联合模型,用遗传算法对联合模型进行了优化。Gour Chandra Mahata、Sujit Kumar De[2]建立了零售商向信用风险客户出售劣质商品的最优批量策略,使零售商在周期内单位时间的总利润与最优采购量的关系最大化。Makoena Sebatjane及Olufemi Adetunji[3]通过建立描述手头问题的成本最小化的库存模型来改善库存管理,实现食品生产链中相当大的成本节约。
随着计算机辅助的库存管理阶段的到来,国内学者在库存管理方面的研究数量和成果也极为可观。江玉杰等[4]提出需求非正态分布下服装产品安全库存决策算法,然后通过具体算例验证该算法的可行性和有效性。研究结果表明,在服装产品生命周期内,提高成熟期内的安全库存和降低衰退期的安全库存,可以减少服装经销商不必要的安全库存;陈啟等[5]研究需求依赖于价格和时尚程度的服装库存模型,考虑体验服务投资可提高服装时尚度、促销降价可改善销售需求的作用,构建一般情形、体验服务投资情形、促销努力情形以及服务与促销联合4种情形下的优化订货和定价模型,分析体验服务投资和促销努力联合时对服装零售商优化决策的影响。
基于上述国内外研究成果,可以看出库存仓储成本对于服装企业成本有着重大的影响。对于需要提供良好服务的服装业而言,拥有完善的库存管理理念、先进的库存管理技术是很重要的。
1 问题描述
通过对美邦进行六力分析和SWOT分析发现,美邦存在严重的库存问题,需要进一步对其服装订货策略进行研究。根据骆杨[6]分析“快时尚”的服装行业的库存控制问题,应当先以库存问题为切入点,分析库存问题产生的原因和服装的需求特点。其次,应采用不同的分类方法,对服装的类别进行分类,分类方法不同,产生的类别也不同。最后,基于服装的分类以及历史销售数据,来预测未来短期服装的需求量。
因此,本文以美邦服装作为研究对象,首先通过数据调研,分析美邦存在的高库存问题;然后使用八爪鱼软件,对天猫美邦专卖店的服装数据进行收集和整理;其次利用多重与多标准ABC分类法进行分类;同时采用数据挖掘等相关技术,建立系统预测模型,并通过MATLAB进行模型计算;最后对不同分类标准的服装进行需求预测和订货策略研究。
本文的组织结构图如图1所示。

图1 组织结构图
2 美邦服饰的多重与多标准ABC分类
传统的服装产品分类主要是按照ABC分类方法,结合产品的生命周期将服装分为3类,如表1所示。

表1 传统服装业的服装产品分类
通过表1可知,传统的服装产品分类方法较简单,但是服装市场已经从原有的批量生产、款式单一发展成种类多、个性化生产[7]。以往服装业的分类方法已经难以满足当今服装市场的需求,因此,在服装业的库存管理过程中,应对服装进行更加细致的划分。
多重与多标准ABC分类方法主要包括多重和多标准两个大的层次[8]。多重ABC分析主要是先进行大类分析,再重点对A、B两类产品进行二重分析,对于C类产品不再进行划分[9]。多标准ABC分类方法主要利用销售量、销售额、利润、库存量等标准进行分类。
根据调研内容进行分析,发现数据中春装和夏装的销售价格普遍低于300元(见表2),按照销售量、销售额进行ABC分类,分类的依据为:

表2 销售量与销售额
A类:销售量/销售额为45%-75%的,累计品种数目为5%-25%;
B类:销售量/销售额为10%-40%的,累计品种数目为15%-45%;
C类:销售量/销售额低于10%的,累计品种数目为45%以上。
依据价格标准分的大类,分别进行销售量和销售额的单标准分类,分类结果如表3、表4所示。
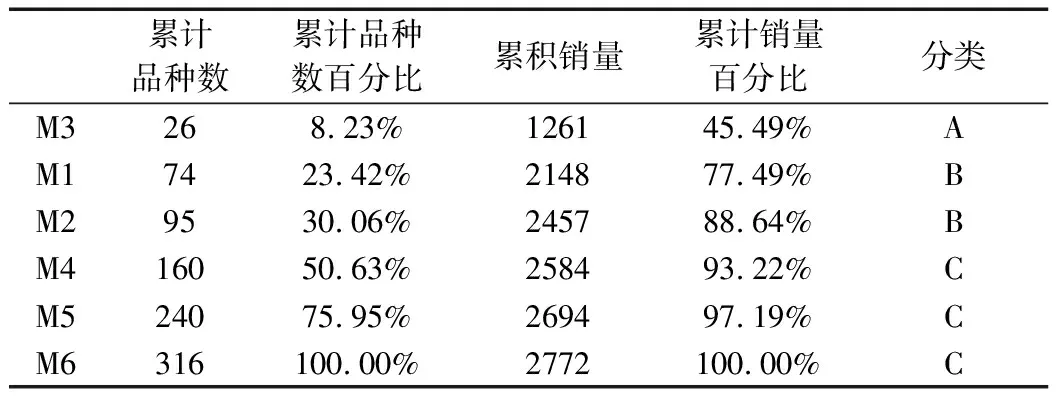
表3 销售量的单标准分类
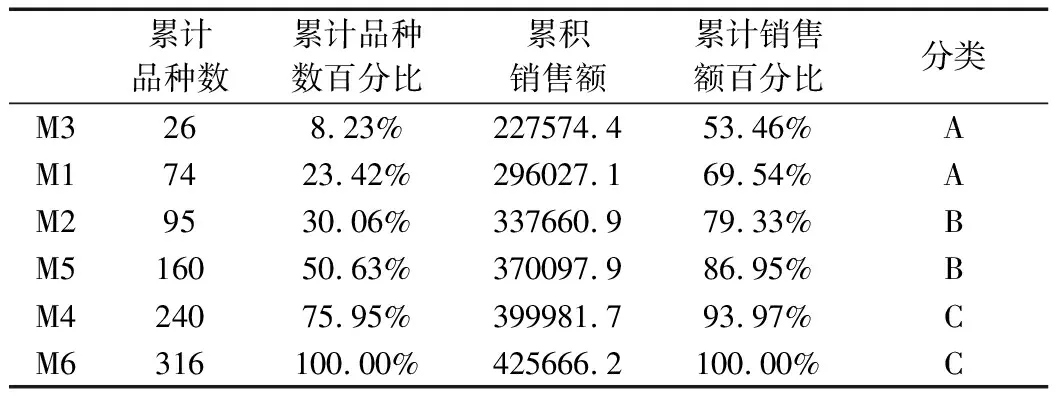
表4 销售额的单标准分类
通过分析,得出多标准ABC分类的结果为M3,M1,M2,M5,M4,M6,如表5所示。因此,对于M3应进行更精确的订货策略分析,严格控制其库存;对于M1和M2应当做到适度控制,适度地减少库存量;对于含有C类的M4、M5和M6,可采用一般的订货管理或根据经验进行预测。本文针对重点管理的M3进行了进一步的分析。
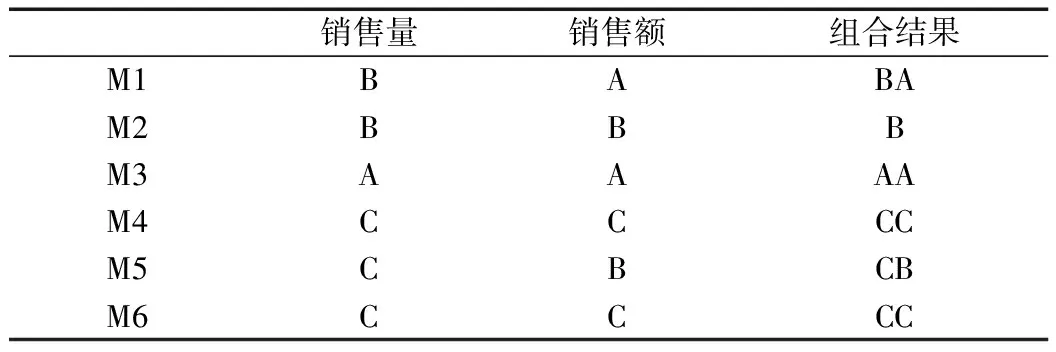
表5 双标准分类
3 基于双标准ABC分类的M3多标准分类
对于M3进行同理的双标准分类,得到的管理顺序为牛仔裤、休闲裤、卫衣、衬衫、裙子、外套、毛衣,如表6、表7所示。

表6 M3的销售量单标准分类
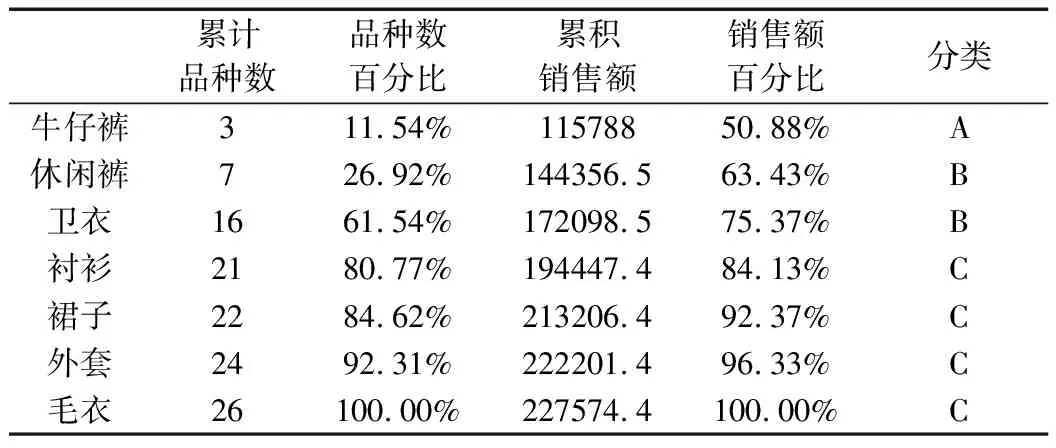
表7 M3的销售额单标准分类
由分类结果可知,应该进行重点管理的是价格适中的牛仔裤。为提高短期预测的精确性,本文采用灰色预测模型进行预测。
4 基于灰色预测的高销量服饰订货策略
4.1 灰色预测模型
灰色预测模型中最常用的是GM(1,1)模型,指的是运用一阶微分方程,对1个变量,利用离散数据建立微分方程的动态模型。
①灰色预测模型的基本公式如式(1)所示。
(1)
式中,x(0)是模型的灰导数;a是模型的发展系数,u是模型的灰色作用量。
②灰色预测模型的矩阵算式如式(2)-(4)所示。
(2)
Y=[x(0)(2),x(0)(3),x(0)(4),…,x(0)(n)]T
(3)
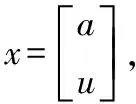
(4)
由式(4)计算出a和u,并得到灰色系统模型的时间响应函数,如式(5)所示。
本组患者50例中,3例因出现并发症或是由于患者本身因素而死亡,其余均顺利在术后7~125天时间内顺利拔管,成功转入康复病房进行康复治疗或者治愈之后顺利出院。
(5)
由公式(5)进行计算,可得到实际数据的模拟序列函数,如式(6)所示。
(6)
公式(6)可以准确地反映原始数列的变化趋势、增长(减少)趋势。当k取1,2,…时,可以求出数据的训练值,当k大于等于n时,可以求得数据的预测值。
③灰色预测模型结果检验,如式(7)-(11)所示。
e为残差检验,A为实际值,G为预测值
e=A-G
(7)
相对残差
q=E(0)(K)/x(0)(K)=e/A
(8)
S1代表均值
(9)
S2代表残差均值
(10)
c代表方差比
(11)
4.2 建模分析
本文调研了一款卫衣在上市的8周内每周的总销量,如表8所示。

表8 卫衣8周内的销量
利用MATLAB进行数据分析,预测结果如图2所示。

图2 灰色预测模型的预测结果
概率P为
(12)
灰色预测公式为

(13)
通过以上的分析,得出灰色预测模型的数据分析结果,如表9所示。发现在概率P=1的情况下,方差比c=0.044846,证明了预测结果优秀。

表9 灰色预测模型数据分析
5 结论
本文是以存在高库存问题的美邦的销售数据为依托,运用多重与多标准ABC分类法,将服装数据进行了更加合理的分类。随后针对重点管理类别中的卫衣销售数据,建立了灰色预测模型,然后利用MATLAB进行求解,对特定时间段的数据进行了预测,获得实际值、预测值、误差等信息。最后,通过概率与误差的关系进行检验。由此,为服装进货数量的确定、库存管理、服务水平等管理决策提供参考价值,以期提高服装企业发展核心的竞争力以及客户的服务质量与水平。

