高校校园无人车快递配送系统设计——以南京林业大学为例

□ 贾熙来，林 丽，屠浩诚，李小格，王艺蒙

(南京林业大学 汽车与交通工程学院，江苏 南京 210037)

《校园快递行业发展报告(2019)》显示[1]，我国高校学生的网购比例正处于爆发式增长阶段，校园快递已成为快递行业中的重要一环。快递行业的总体服务质量虽然日益提高，但是在校园的配送服务中仍存在“最后一公里”问题。高校快递具有数量多、增长速度快、用户的期待度高等特征；目前，高校内用户大多仍采用集中或分散快递点自取的方式取件，校内用户收发快递多以步行为主，路线较为单一，且校内道路状况较差，当用户寄取的快递过重、步行距离过长时，用户的舒适度将大幅降低。现阶段，鲜有对于无人车配送在校园内应用的研究，研究多集中于无人车在外部复杂道路或封闭空间内的应用，如美团公司近期推出的新一代无人配送车“魔袋20”，具有L4级别自动驾驶能力，其在疫情期间无接触配送中发挥了巨大作用[2]，但由于此类无人车成本高，运量小，对道路状况、路侧设施要求高，行驶中对道路影响较大，因此在校园快递的配送中难免显得大材小用。

本文针对高校内快递数量、道路情况等，从路线确定，运行方式两方面入手，设计了一套更适用于校园的自动化配送系统。此系统提供了“最后一公里”的配送服务，能够有效分担集中快递点的运营负担，并解决学校用户群体的“取件难”问题。

1 南京林业大学校园的快递小区划分及调查分析

以南京林业大学本部校区为例，多数用户与快递点间距较远、快递收取不便、快递点集中、取件人数较多；各类电商活动期间，快递量激增导致快递点超负荷运转、用户排队时长延长，同时造成了大量的人员聚集，不仅使快递点的运转效率低下，也存在一定的安全隐患。为更好了解校内快递运营的整体情况，本文采用问卷调查法对各区域进行研究。

1.1 快递小区的划分

根据南京林业大学的学生宿舍区域划分办法，对学生宿舍Ⅰ、Ⅱ、Ⅲ区进行更细致的划分，将其中间距较小、人数相近的建筑单位合并为一个小区；根据问卷调查中所得快递量对划分区域进行修正，若其中部分建筑吸引的快递量过少，则将其并入临近的快递小区；确定小区快递集散点后，其服务能力、服务范围应能够满足整个快递小区的需求，具体分类结果如图1。

图1 快递小区分布图

1.2 问卷调查及现状分析

本文研究的服务对象包括在校师生和校内居民，约36000人。该问卷对现阶段校内用户的快递收发方式、效率、件数、规格、校内居住地、用户的满意度以及用户年平均取件数等方面进行抽样调查。为保障调查结果的准确性，除进行网络问卷调查之外，还在校内不同区域进行随机询问调查，共得到问卷345份，其中有效问卷306份，有效率约88.69%；有关快递点现状的具体结果如图2所示。

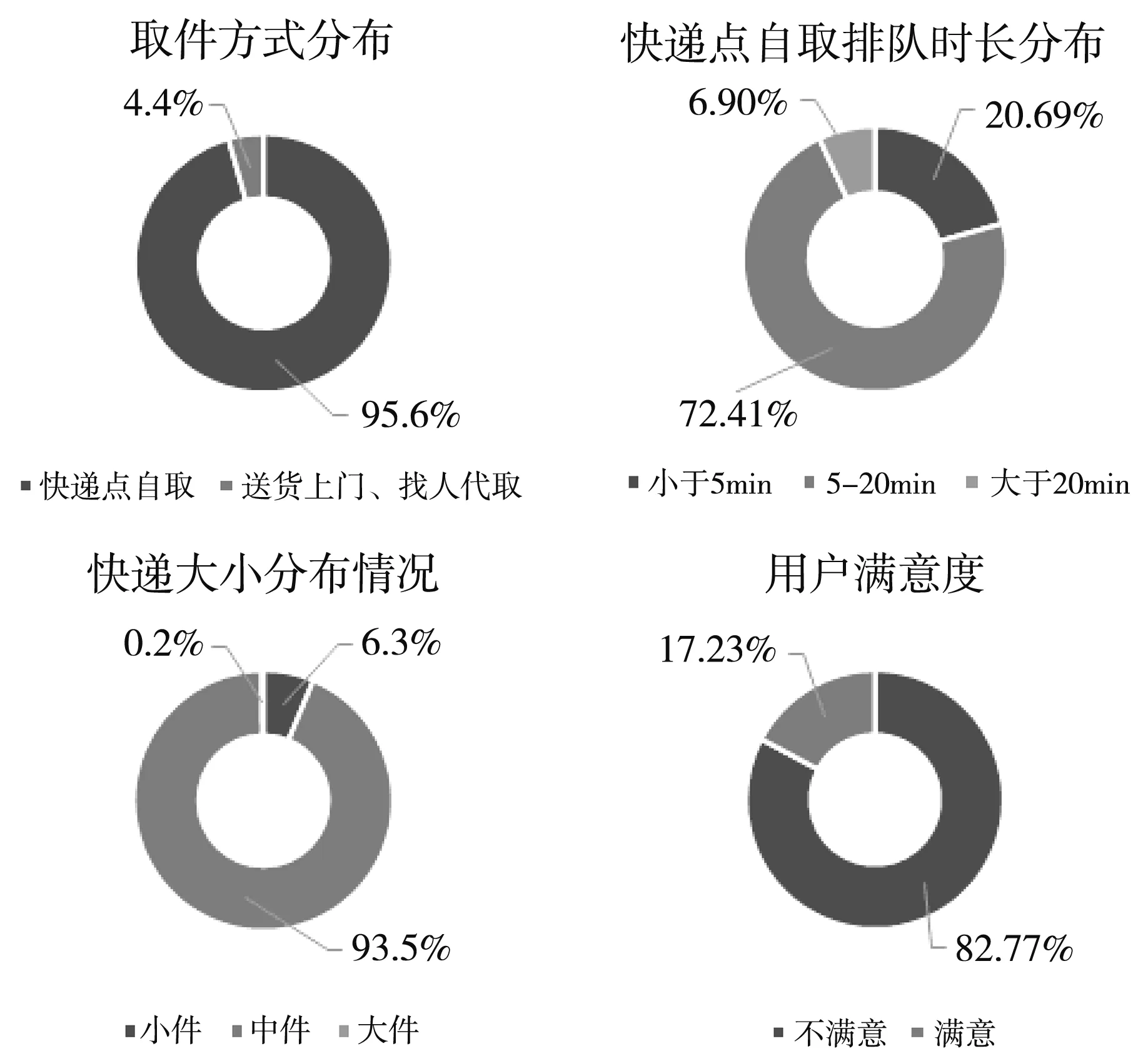
图2 问卷调查结果

1.3 具体小区快递吸引量的调查

整理问卷调查数据后，可得出各小区的快递吸引量如表1所示。

表1 问卷调查结果与分析

各宿舍楼栋日平均快递吸引量的计算:

(1)

式(1)中，Rn为每楼栋人数，Kn为各楼栋平均每日产生的快递量，Gi为小区的实际快递吸引量，n为楼栋编号，得出的各楼栋的日均快递吸引量如图3所示。

图3 校内各楼栋日平均快递吸引量

2 快递集散分布模型的建立及应用

2.1 模型总体坐标的分析

根据前文所划分的六个快递小区，按理想化状态下快递的集散分布，以校园北三门作为坐标原点，建立空间坐标系，将各小区内每个楼栋的主要出入口记为该单位楼栋的快递集散坐标点，该点在三维坐标系中具有绝对坐标(x,y)；将式(1)中所述的快递分担量Kn作为该楼栋在三维坐标系中的绝对坐标Z，在软件内完成相应网点的标定，建立小区的三维模型。

2.2 模型形心的计算

根据各小区的三维模型，建立快递小区的三维矩阵Di,Di为第i个小区内的三维坐标矩阵，小区内有n个楼栋的坐标集散点，具体形式如式(2)所示：

(2)

将Di带入公式：center=mean(Di)，计算形心坐标，得到每个快递分布小区的形心坐标点(x,y,z)，具体结果如表2。

表2 小区形心点坐标

2.3 快递集散点位置的确定

将各小区三维图形的形心在校园平面内的投影点作为该小区内快递集散点设置的最优点。但考虑实际校园道路交通和环境的影响，应排除校园道路、建筑、绿地等设施，选取投影点附近合适的位置设置该小区的快递集散点。此外，由于小区③各楼栋距快递发出点小于100m，故不列入此次的模型中进行计算。将所得结果进行覆盖模型的验算，并与黄媛等[3]提出的智能快递柜布置结果进行对比选择后，得出六个快递小区的快递集散点布置情况如图4所示，各集散点的三维坐标(x,y,z)如表3所示。

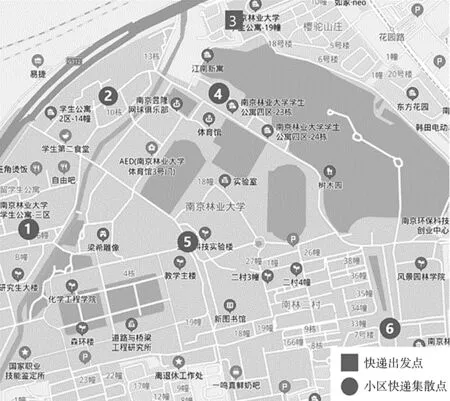
图4 快递集散点布置图

表3 快递集散点布置情况及坐标

3 无人车配送最优路径的确定

3.1 构筑校园内道路网路模型图

对校园内各快递集散点之间最短距离的计算可采用Dijkstra算法[4]，为简化算法的求解过程，提升运算速度，从而实现对最短路径的求解，首先需构筑校园内道路的建筑模型图。从校园地图中提取由快递发出点作为起点，通往或途径各小区快递集散点的有效路径，将其抽象化形成具体的校园道路联通网络模型，以两条道路的交叉点为节点，将道路进行分段，获得相应的顶点集合V={1,2,3,…,18,19}，具体结果如图5所示；并在网络模型图中获取由各个顶点截取的各路段长度，以其作为各路段的权值，建立权矩阵，如图6所示，带入算法内进行计算。

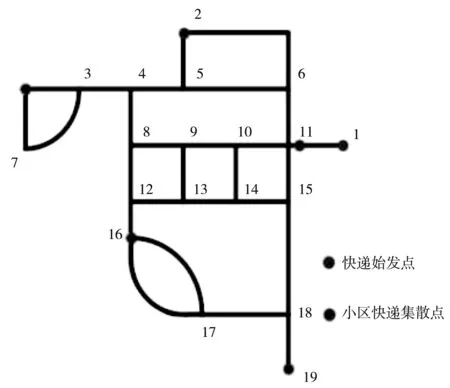
图5 校园道路联通

图6 各点间道路权矩阵

3.2 算法实现过程

算法的主要目的是得出两个顶点之间的最短路径，在该项目中，拓展应用为确定一个顶点作为源节点，计算从该顶点出发，经过图中所有其他节点的最短路径，产生一个最短路径图。

具体实现过程如下：

(1)将校园中所有经过计算后确定的快递次级集散点及其之间的通路画为有权重的有向图G;

(2)将北三门快递总集散点设为源节点A1；集合A存放图G中的所有顶点；集合E存放图G中的所有边，通过两个顶点形成的有序元素对(Ai，Aj)表示从顶点i到j有路径相连，而边的权重则通过计算集散点之间的距离得出。其中，任意两点间路径的权重为该路径上所有边的权重总和;

(3)学校的所有快递集散点组成的集合为A，从源点开始，算法不断地选取集合A-E中具有最小路径的顶点Ai：

①将源点A1加入集合A;

②遍历该点的所有邻接点，找到与源点之间路径最短的顶点放到新的集合A′中(初始状态时，集合A′中只有源点A1)，随着遍历过程不断重复，每次都会找到一个新的不重复的顶点放入A′中，直到所有顶点全部加入集合A′中;

③重复上述遍历过程，直到所有顶点全部加入集合A′中[5]。

3.3 最短路径结果

最终经计算后得出快递配送的最短路径为1>11>6>2>5>4>3>7>3>4>8>12>16>17>18>19>18>15>11>1(从北三门出发最后回到北三门)，最短路径长度约为3545米，具体结果如图7所示。

图7 最佳联通路径

4 无人车线路的分析

无人快递车能否在校园内正常运营，取决于无人快递车的运输能力能否满足需求，能否正确地处理运营线路上人、车、路之间的关系。通过我国快递业务增长趋势预测校内快递增长，分析未来校内快递增长率，考虑无人车载运量和运行方式，最终规划运营线路。

4.1 快递增长趋势预测

由于校内各快递小区的每年常驻总人数无明显变化，结合前文问卷，将快递数量增长情况的调查结果带入式(3)计算，所得结果如图8所示。

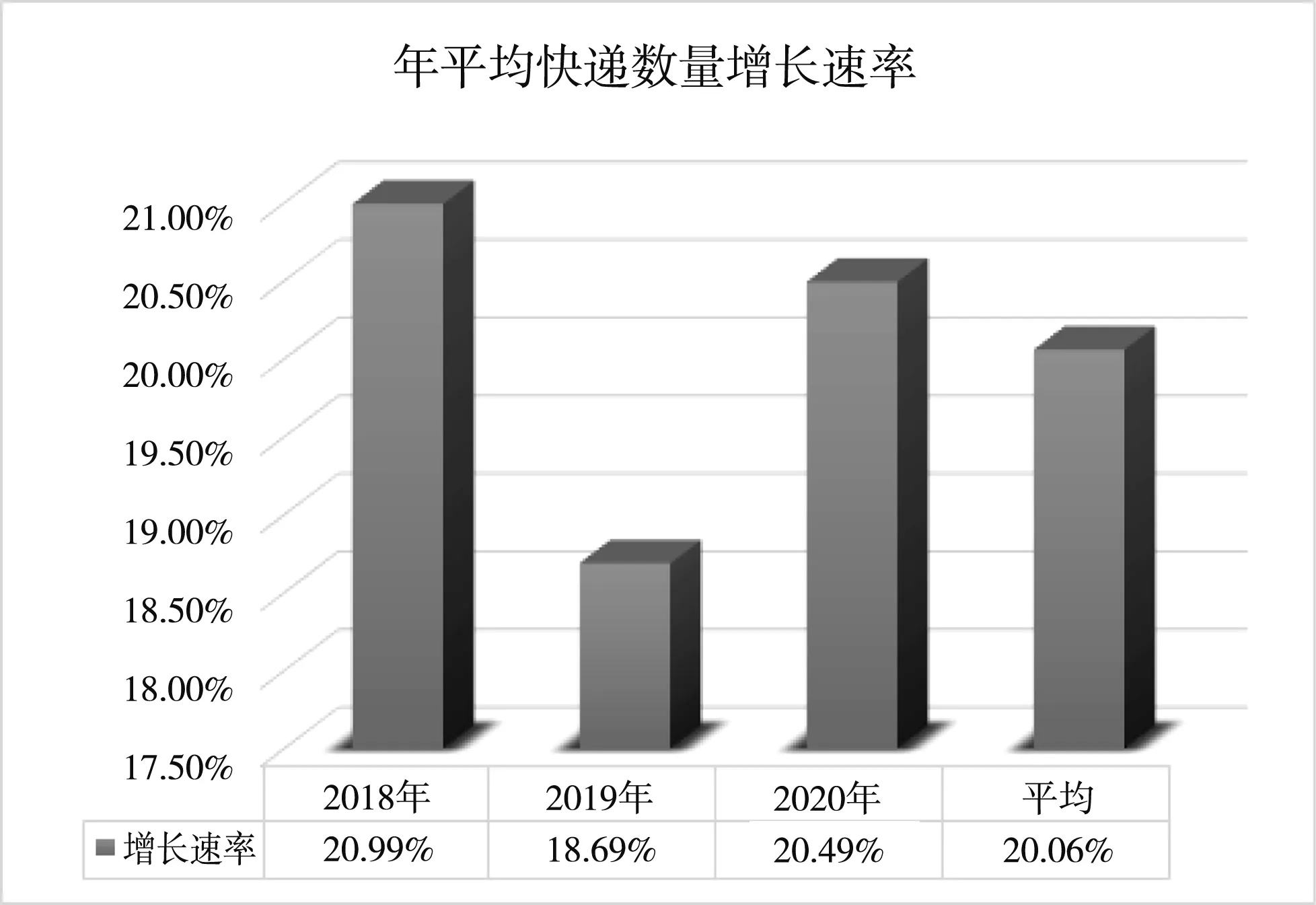
图8 校园年平均快递增长速率

(3)

近年来校园内快递数量的增长率约为20%。在线路设计中应考虑到此系统的未来服务水平，并结合校园未来发展规划，故仅对未来五年内各快递小区的日平均快递吸引量进行预测，作为未来线路数及投放设备量的规划依据，具体结果如表4所示。

表4 未来5年各小区的日平均快递吸引量 (单位：件)

4.2 无人车具体运营方式

由于现阶段市面上使用的无人车不适用于高校，故本文方案拟选用磁导航AGV，具体形式如图9所示，其具有成本低、效率高、控制简单、技术成熟度高、抗干扰能力强等优点，运行方式采用在预制构件内铺设磁性地标，由位于车辆底部的磁敏传感器识别路线，实现对道路的指引[6]。由于现阶段AGV的运行条件较为严格，可采用地下共同沟的方式来满足AGV对运行环境封闭无影响和路面平整度的要求[7]：将预制构建按规划线路方向埋设于道路两侧的人形通道下，仅在小区快递集散点附近合适区域设置开口，进行装卸货作业。共同沟形式如图10所示。

图9 双向潜伏式磁导航AGV

图10 校内地下共同沟布置图(单位：cm)

此方案的优点在于能大幅提高运量以及配送效率，运营过程中的所有路线均与地面道路具有上下层次的空间关系，有效的避免了AGV在路表运行时与行人的相互影响，可以同时收纳市政、电力、通讯、给排水等各类管道设施，方便检查与维修[8]。

4.3 无人车的载运量

无人快递车运载量模型的计算公式：

(4)

式(4)中，N代表一辆无人车装载的快递数量；V代表一辆无人快递车的装载体积；a、b、c分别代表大、中、小件包裹的体积，关于大中小快递划分标准根据校内快递点标准快件的体积与质量分析评估得到。结合无人快递车的装载体积的计算公式和前文问卷调查已知的大、中、小件快递的占比，可以估计160cm×100cm×30cm无人快递车的平均每次载货量在35件，并可采用两车拼接等方式提升运量。

4.4 无人车的运营线路规划

结合前文所得最优路径、集散点位置等要素，以及校内具体道路情况，采取最短路交通流分配法，对小车运送区域的最优路径进行划分；在运行中最少需要使用三台设备进行运送作业，其中，一号小车负责小区②(学生公寓二区)和小区⑤(主要教学区)；二号小车负责小区①(学生公寓一区)和小区④(北大山公寓)；三号小车负责小区⑥(南大山公寓)；具体线路划分如图1所示。理想状态下，根据校园地图距离和无人快递车的配速可得其配送距离及时间。经计算后，需以每年三辆的速度增加,才能满足校园内的快递增长需求。

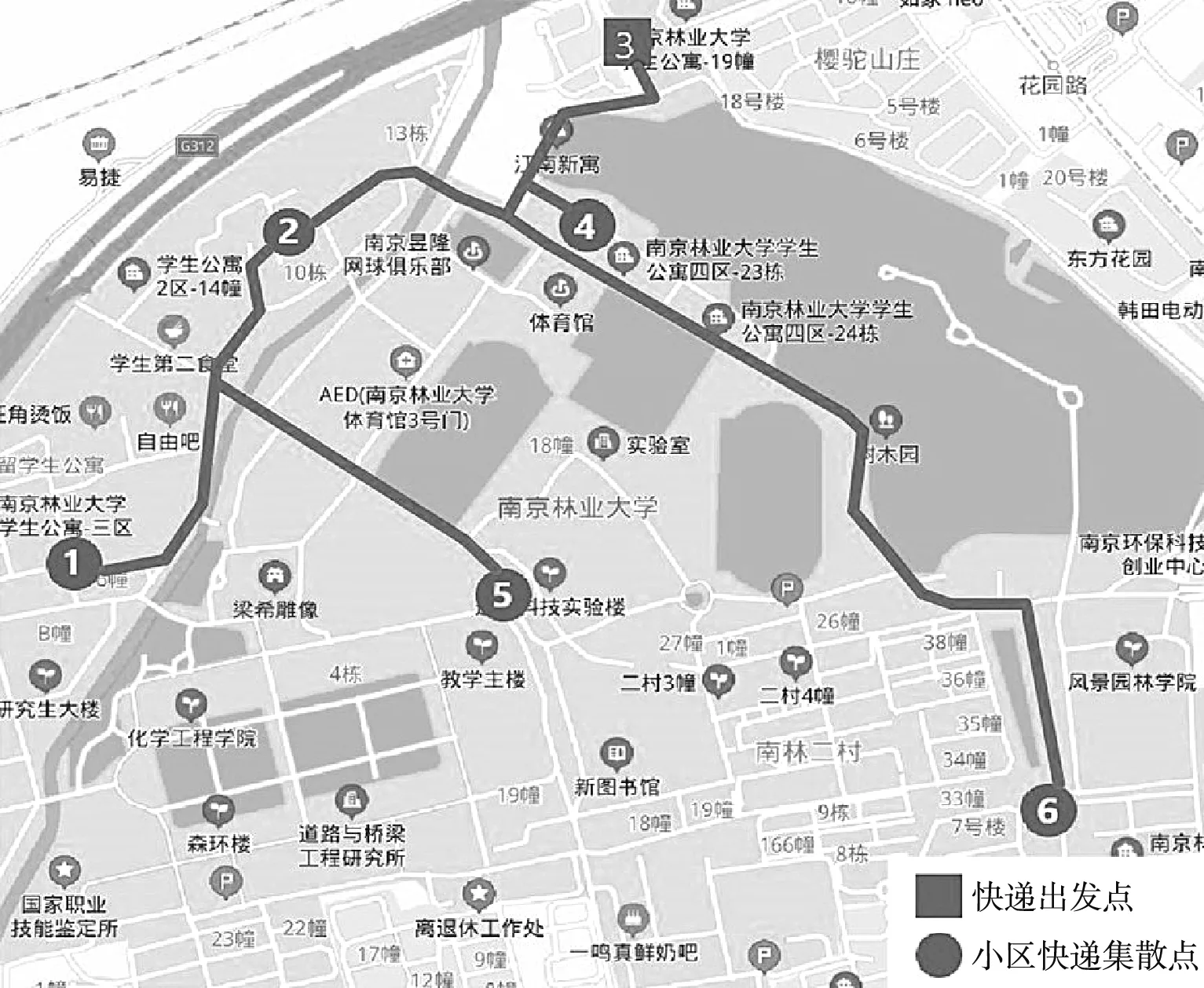
图11 具体最优线路

5 总结与展望

本文基于南林校园本部校区，划分快递小区，以快递分担量为权重建立了快递集散分布模型，确定了各小区的集散点，使之满足服务半径要求；并以道路长度为权值，采用Dijkstra算法模型对校园最优路径进行建模计算，提出以地下共同沟的方式从空间上解决了无人车运营时与行人的冲突，解决校园上课高峰时间和道路用地因素对运输效率的影响，为校园新的快递运输方式的应用提供建议，促进校园内快递物流的高效发展。

但论文在研究过程中，仅以南京林业大学为例建立模型，并未将模型应用于其他校园，故主观性较强，较为理想化；且本系统仍需要结合校园内道路的具体路况、路侧行人数等因素加以检验和改进，在面对更为复杂的路网情况时，可在本文两种算法的基础上使用蚁群算法提升运算结果的准确性以及运算速度；考虑到在校师生对智能化平台的接受度与普及率高，未来应加入小程序优化系统，实现智慧物流；为确保系统的经济性，应根据实际工程需要对系统进行优化。