弱电网下基于DSOGI-PLL的并网换流器频率耦合阻抗建模与稳定性分析
史金柱,杨黎晖,朱美婷
(西安交通大学 电气工程学院,陕西 西安 710049)
0 引言
近年来,中低压直流配用电系统大规模接入电网,三相电压源型换流器(VSC)作为中低压直流系统并网常用的接口电路,发挥着重要的作用,其稳定性问题也受到越来越多的重视。经过长距离输电后,交流电网易呈现弱电网和三相不平衡特性[1]。在并网系统中,通常使用锁相环对电网基波分量进行锁相,为控制系统提供相位基准。与传统的单同步坐标系锁相环相比,基于双二阶广义积分器(SOGI)的锁相环(DSOGI-PLL)能够在三相不平衡以及系统谐波复杂的情况下进行准确锁相[2-3],为控制系统提供正确的相位信息,因此受到广泛关注。
在弱电网下,电网阻抗不可忽略,并网换流器非常容易与电网发生交互作用而造成系统振荡,严重影响中低压直流系统的安全稳定运行。基于阻抗的分析方法是研究并网换流器与电网交互稳定性问题的一种有效方法[4-6],且被广泛采用。传统的阻抗建模方法仅针对同频响应。在近些年的研究中发现,并网换流器中dq轴控制不对称和正弦脉宽调制(SPWM)环节都会产生频率耦合效应[7-8],即系统对于某个频率的扰动,会出现2 个在频率上相互耦合的响应。故需要引入考虑多个频率分量进行频率耦合的阻抗建模方法[9]。而且这种单输入多输出的特性使得原本单输入单输出的稳定性判据不再适用[10],需要考虑频率耦合效应对稳定性判据进行改进。
在频率耦合特性研究方面,文献[11]首先指出电网阻抗会引发dq轴控制不对称并产生谐振。进而文献[12]将其定义为基频的边带谐振,并进一步指出锁相环与电网阻抗相互作用会增强频率耦合特性。在考虑频率耦合特性的并网换流器建模方面,文献[10,13]分别考虑锁相环、直流电压外环、电流内环不对称等多种频率耦合因素,建立了详细的频率耦合阻抗模型,其基于阻抗矩阵分别利用广义奈奎斯特稳定判据和求解行列式零点的方法进行稳定性分析。文献[14]通过扰动频率和耦合频率下等效电路的稳定性来判断整个系统的稳定性,在一定程度上简化了稳定性分析过程。文献[15-16]进一步推导了考虑频率耦合效应的并网换流器系统等效正负序阻抗模型,实现了正负序的等效解耦,从而可以使用单输入单输出的奈奎斯特稳定判据进行稳定性分析。文献[17]利用等效单输入单输出阻抗与电网阻抗的伯德图进行稳定性分析。目前利用等效单输入单输出阻抗模型进行稳定性分析的方法被广泛采用。然而,目前关于频率耦合特性和稳定性的研究都是针对基于传统单同步坐标系锁相环的换流器,而针对在电网电压不平衡和高次谐波较多的情况下广泛应用的DSOGI-PLL 研究较少。DSOGI-PLL 的SOGI 对于低频信号的衰减不够,比较容易引发低频谐振;并且DSOGI 环节会对锁相回路dq轴控制不对称引起的频率耦合特性产生影响。这些因素都增加了基于DSOGI-PLL 的并网换流器频率耦合特性和稳定性分析的难度。
本文首先推导了DSOGI-PLL 的频率耦合模型,然后综合考虑引起频率耦合效应的多种dq轴控制不对称因素,建立了基于DSOGI-PLL 的三相并网换流器的频率耦合阻抗模型,并通过扫频验证了频率耦合阻抗模型的准确性。根据扰动频率和耦合频率下的电路,推导出等效单输入单输出的奈奎斯特稳定判据,并说明了考虑频率耦合效应对于稳定性分析的重要性,然后分析了弱电网下各运行参数对基于DSOGI-PLL 的并网换流器稳定性的影响。最后对并网变流器详细模型进行仿真,验证了所提频率耦合阻抗模型和理论分析的正确性。
1 基于DSOGI-PLL的并网换流器
本文分析的对象为中低压直流配电系统基于DSOGI-PLL 的并网换流器,其主电路拓扑如附录A图A1 所示。并网时采用LC 滤波器,直流侧采用纯电阻来对实际电网缓慢变化的负荷进行简化模拟。
1.1 DSOGI-PLL

1.2 控制器
并网换流器采用电网电压前馈解耦的电压电流双环控制器进行建模和分析,其中外环控制器采用定直流电压控制以维持直流侧电压的稳定,控制结构如附录A图A2所示。
2 频率耦合阻抗模型
首先推导对称电网下考虑频率耦合效应的并网换流器阻抗模型。PCC处a相电压为:

式中:Daλ、φaλ分别为相量幅值、相位。扰动频率和耦合频率关于2倍电网基频互补,即fp+fp'=2f1。
2.1 并网换流器数学模型
以a 相为例,由图A1 所示并网换流器主电路拓扑可得并网换流器数学模型为:
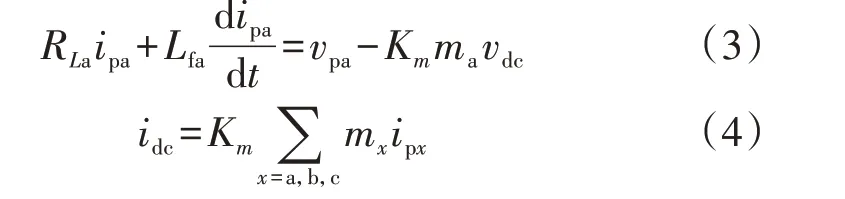
式中:ipx为PCC 处电流;RLa、Lfa分别为滤波电感等效电阻、滤波电感;Km为调制系数;mx为调制信号;idc、vdc分别为直流侧电流、电压。
2.2 DSOGI-PLL数学模型
对PCC处电压进行锁相可得整个系统的基准相位,故锁相环的频率特性对整个系统的稳定性有很大的影响。由图1(a)所示SOGI 控制框图可得经SOGI 处理后两路输出电压信号v'、q'v'与输入电压信号之间的传递函数分别为:

图1 SOGI及DSOGI-PLL控制结构Fig.1 Structures of SOGI control and DSOGI-PLL control

式中:sλ=j2πfλ;Gαλ(sλ)=G(sλ)+jq'G(sλ);Gβλ(sλ)=q'G(sλ)-jG(sλ);vλ为频率fλ下的输入电压信号。忽略高阶小信号量,经αβ/dq变换,v+d、v+q分别为:

式中:Tp(s)、Tp'(s)分别为DSOGI-PLL中fp、fp'下输入电压信号的传递函数,其表达式见附录B 式(B1)、(B2)。
2.3 控制器数学模型
控制环节包括派克变换、直流电压外环、电流内环、反派克变换以及调制环节,其数学模型见附录B式(B3)—(B15)。
2.4 阻抗模型
由并网变流器主电路的拓扑结构,列出扰动频率和耦合频率下并网换流器的数学模型分别为:

式中:A1—D1、A2—D2为阻抗系数,其表达式见附录B 式(B16)—(B23)。求解式(14)、(15)可得基于DSOGI-PLL的并网换流器的阻抗、导纳矩阵分别为:
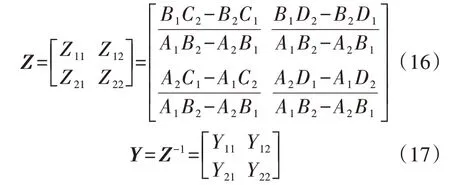
2.5 仿真验证
对中低压配电系统而言,直流侧电压等级通常在600~800 V,本文设直流侧额定电压为800 V,交流侧的电压等级为220 V/380 V。并网换流器的其他参数如附录C 表C1 所示。并网变流器阻抗模型的理论结果和扫频结果对比情况如图2 所示。由图可知,扫频结果与理论推导出的阻抗曲线非常吻合,验证了阻抗模型理论推导的准确性。

图2 并网换流器阻抗模型的理论与扫频结果对比Fig.2 Comparison of theoretical and frequency scan results for impedance model of grid-connected converter
3 阻抗模型特性分析
由第2 节的阻抗模型理论推导和扫频验证结果可知,阻抗矩阵是对称的。故在对阻抗模型进行分析时,只需要对Z11和Z12进行分析。
3.1 DSOGI-PLL对频率耦合特性的影响
对于DSOGI-PLL 而言,DSOGI 环节的阻尼系数和锁相回路带宽对频率耦合特性均有影响。一方面,阻尼系数是DSOGI 环节独有的系数,其对频率耦合特性产生影响的同时也影响了并网换流器的阻抗特性;另一方面,DSOGI环节的存在也影响了锁相回路带宽对频率耦合特性的影响。因此本节从锁相回路的带宽和阻尼系数2 个方面分析DSOGI-PLL 对频率耦合特性的影响。
附录D 图D1 为70、100、150 Hz 这3 种带宽下基于DSOGI-PLL 的并网换流器的阻抗曲线。可以看出,在低频段随着锁相回路带宽的增大,自阻抗Z11幅值增大的同时耦合阻抗Z12幅值有所减小。附录D 图D2 为不同阻尼系数下基于DSOGI-PLL 的并网换流器的阻抗曲线。可以看出,随着阻尼系数的增大,自阻抗Z11和耦合阻抗Z12的幅值均有所减小。
耦合阻抗减小说明了耦合频率响应更加明显,因此可以得出结论,在低频段随着锁相回路带宽和阻尼系数的增大,基于DSOGI-PLL 的并网换流器的频率耦合特性更加明显,忽略频率耦合效应会使得低频段稳定性分析产生较大的误差。
3.2 直流电压环带宽对频率耦合特性的影响
影响直流电压环带宽的主要因素是直流侧滤波电容和直流电压环PI 控制器参数,因此本文分别分析这2个因素对频率耦合特性的影响。
附录D 图D3 为直流电压外环控制器中不同PI控制器比例系数kvp下的并网换流器的阻抗曲线。由图可知:在低频段自阻抗Z11的幅值随PI控制器比例系数增大而增大;耦合阻抗Z12则随着PI控制器比例系数的增大而减小。附录D 图D4 为滤波电容不同时并网换流器的阻抗曲线。由图可知:在低频段自阻抗Z11随着直流侧滤波电容减小而增大;耦合阻抗Z12则随着电容的减小而减小。因此可以得出结论,直流电压环的带宽越大,即PI 控制器的比例系数越大或直流侧滤波电容越小,耦合阻抗越小,并网换流器的频率耦合程度越深,当进行稳定性分析时忽略频率耦合特性造成的误差越大。
3.3 电流内环不对称对频率耦合特性的影响
电流内环不对称也是一个重要的dq轴控制不对称的影响因素,其主要是由于在实际的运行过程中PI 控制器参数设定不同或者其他系统因素引起的。附录D 图D5 为不同带宽比(d轴电流带宽与q轴电流带宽之间的比值)下的阻抗曲线。由图可知,在低频段随着带宽比的增大,自阻抗Z11增大,耦合阻抗Z12减小,频率耦合程度加深。但是相较于其他dq轴控制不对称因素,电流内环不对称对频率耦合特性的影响有限。
4 阻抗模型稳定性分析
根据第3 节分析结果,在低频段频率耦合效应是不可忽略的,并且频率耦合效应的存在改变了系统的输入输出关系,原本正负序解耦的单输入单输出奈奎斯特稳定判据不再适用。对于这种多输入多输出系统,目前分析其稳定性的常用方法有2 种:方式1 为直接使用广义奈奎斯特判据对第2 节所推导的阻抗矩阵进行分析;方式2 为对阻抗矩阵进行处理,转化为等效解耦的正负序阻抗使用单输入单输出的稳定性分析方法进行分析[15-18]。为了便于分析弱电网下并网换流器的稳定性,本文采用方式2,首先推导了等效解耦的换流器输入导纳,进而使用单输入单输出的奈奎斯特稳定判据进行稳定性分析。
4.1 稳定性判据
附录E 图E1 为扰动频率和耦合频率下的等效电路。列出这2 个电路的电压、电流方程,处理后可得并网换流器的等效输入导纳YVSC为:

式中:vs为电网等效电压源的电压;ZVSC为并网换流器的等效输入阻抗;iVSC为并网换流器等效电流源的电流。由式(19)可知,当电网和并网换流器能够独立稳定运行时,并网稳定性取决于Zgf/ZVSC。当正、负序阻抗比都满足奈奎斯特稳定判据,即正、负序奈奎斯特曲线都不包围点(-1,0)时,并网换流器能够稳定运行。
4.2 稳定性分析
4.2.1 等效电网阻抗对系统稳定性的影响
对于中低压直流配电系统而言,经过长距离的输电,由线路阻抗和变压器阻抗组成的等效电网阻抗不可忽略,交流电网呈现弱电网特性。故有必要分析等效电网阻抗对于中低压直流系统稳定性的影响。
附录E 图E3 为不同短路比下正、负序阻抗比的奈奎斯特曲线。由图可知,当短路比不断减小即等效电网阻抗不断增大时,正、负序奈奎斯特曲线越来越容易包围点(-1,0),这说明了系统的稳定性在不断变差。当短路比减小到1.9时,奈奎斯特曲线开始包围点(-1,0),根据奈奎斯特稳定判据,此时系统不稳定。因此可以得出随着电网变弱,并网换流器系统的稳定性变差,系统愈发容易失稳的结论。
4.2.2 DSOGI-PLL对系统稳定性的影响
附录E 图E4、E5分别展示了DSOGI-PLL 的锁相回路带宽以及阻尼系数对并网换流器稳定性的影响。设Lg=9 mH,由图可知,随着DSOGI-PLL 锁相回路带宽的增大和阻尼系数的增大,正、负序奈奎斯特曲线越来越接近点(-1,0)。相较于锁相回路带宽,阻尼系数对并网换流器系统稳定性的影响更加严重。故阻尼系数和锁相环参数的选取要考虑基于DSOGI-PLL 的并网换流器的稳定性影响,不能只追求其动态响应速度。
4.2.3 直流电压环带宽对系统稳定性的影响
附录E图E6、E7分别展示了滤波电容以及PI控制器比例系数对于并网换流器稳定性的影响。设Lg=7 mH,由图可知,当滤波电容减小至1 175 μF 时和PI控制器的比例系数增大至1.5时,奈奎斯特曲线包围了点(-1,0),系统失稳。即当直流电压外环的带宽增大时,正、负序奈奎斯特曲线更加容易包围点(-1,0),并网换流器的稳定裕度变小,因此在实际的直流系统中,直流电压外环的参数选择要综合考虑直流外环的动态响应与稳定性,PI 控制器的比例参数取值不宜过大,而直流侧滤波电容取值不宜过小。
4.3 仿真验证
为了验证本文推导的频率耦合阻抗模型的准确性,根据附录E 表E1 的参数,分别给出不考虑频率耦合和考虑频率耦合特性的正、负序阻抗比的奈奎斯特曲线,如图3 所示。由图可知,不考虑频率耦合时,正序阻抗比的奈奎斯特曲线没有包围点(-1,0),这说明传统的阻抗分析方法认为系统是稳定的。但是考虑频率耦合时,正序阻抗比奈奎斯特曲线包围了点(-1,0),且与单位圆的交点处的频率为93 Hz,这说明此时系统是不稳定的,且振荡频率分别为93 Hz和与93 Hz耦合的7 Hz。

图3 考虑与不考虑频率耦合特性的奈奎斯特曲线Fig.3 Nyquist curves with and without considering frequency coupling characteristics
由附录E 表E1 所示参数在MATLAB/Simulink平台建立图A1所示系统的详细模型,并进行时域仿真。PCC 处电流时域仿真波形和快速傅里叶变换(FFT)分析结果分别如图4、5所示。结果表明,并网点发生了低频振荡,且振荡频率与本文考虑频率耦合效应模型所预测的7 Hz 和93 Hz 吻合。与传统的阻抗模型和分析方法相比,本文所推导的频率耦合阻抗模型及进行的相关理论分析更加准确有效地判断了基于DSOGI-PLL 并网换流器与弱电网之间的稳定性。

图4 并网换流器PCC处电流的时域仿真结果Fig.4 Simulative result of time-domain current waveforms of grid-connected converter at PCC

图5 并网换流器PCC处电流的FFT结果Fig.5 FFT result of current of grid-connected converter at PCC
5 结论
针对中低压直流系统与弱交流系统的交互稳定性问题进行了研究。本文的主要工作是建立基于DSOGI-PLL 的并网换流器的频率耦合阻抗模型,完整分析了关键参数对于频率耦合特性的影响以及弱电网下并网变流器运行的稳定性,并利用时域仿真对建模和稳定性分析结果进行了验证。得出以下结论:
1)DSOGI-PLL 的锁相回路带宽和阻尼系数越大、直流侧滤波电容越小、电压环PI 控制器比例系数越大、电流内环越不对称,并网换流器的频率耦合特性越明显;
2)根据所推导的等效奈奎斯特稳定性判据,证明了考虑频率耦合对于稳定性分析的重要性,并分析了系统各运行参数对于并网换流器稳定性的影响,DSOGI-PLL 锁相回路的带宽及阻尼系数越大、电网阻抗越大,直流电压环带宽越大,系统越容易失稳;
3)分析了所建模型与对称弱交流电网的交互稳定性,建立电网不对称工况下基于DSOGI-PLL 的并网变流器阻抗模型,并研究其与弱电网的交互稳定性问题,考虑符合实际电网的变化的混合负荷分析稳定性问题将是未来进一步的研究工作。
附录见本刊网络版(http://www.epae.cn)。

