猕猴伸展抓握过程中的spike与LFP锁相相位分布特征分析
刘秀玲,郭天翔,王洁,孙洪吉,熊鹏
(1. 河北大学 电子信息工程学院,河北 保定 071002;2. 河北省数字医疗工程重点实验室,河北 保定 071002;3.军事科学院军事医学研究院 军事认知与脑科学研究所,北京 100850)
大脑神经元的主要活动包括单神经元的动作电位和由突触电位形成的局部场电位.单神经元动作电位反映单细胞的电活动,这种通过神经轴突流动的电信号是神经信息传输的基础;局部场电位反映一定范围内的局部电活动.相位是LFP(localfield potential)的重要特征之一,锁相即相位锁定,表示2个信号间的相位同步性.spike的发放和LFP的节律之间的锁相关系包含了重要的神经编码信息[1].
Alex等[2]利用spike与LFP的beta节律的锁相特点对猕猴行为状态和脑网络活动变化性的关系进行了分析. García等[3]利用spike和LFP的锁相研究在听觉皮层对刺激的处理中spike和LFP的相干性动力学. James等[4]利用2个脑区特定功能相关频带下多神经簇的发放与LFP的锁相关系以研究大鼠癫痫模型中梨状皮层和内侧丘脑的放电模式. Sritharan等[5]将spike和场电位的相干性和锁相统计数据作为量化研究初级感觉皮层神经元对2种不同纺锤波的作用. Guillem等[6]在研究大鼠前额叶皮层可卡因的使用与非药物奖励的个体偏好中,使用前额叶皮层的单神经元活动与theta段振荡的锁相时间机构作为研究方法之一.马维建等[7]在大鼠海马体中用锁相关系的变化证实了深部脑刺激技术所使用的电脉冲高频刺激可以改变spike的病理性发放.
因此,spike与LFP的锁相关系的研究对理解大脑神经信息编码具有重要意义.以上对锁相关系的研究证实了在多种大脑活动中spike与LFP锁相的存在性,并且利用锁相关系对大脑活动做了进一步分析,但关于锁相关系中锁相相位的分布特征的分析还比较匮乏.
基于这种情况,本文利用猕猴伸展抓握运动范式,在多个脑区内,对猕猴在实际运动中的峰电位与局部场电位的锁相相位变化进行了分析,为利用锁相解析运动中的神经编码信息提供了新思路.
1 材料
1.1 实验信号采集
本实验数据来自2只猕猴:猕猴A和猕猴B,M1、S1、PPC共3个脑区的3 d实验的spike发放时间数据(spike timestamp)和LFP信号,所有实验动物和实验数据均来源于军事科学院军事医学研究院实验动物中心[8].
剔除噪声过大数据后,共使用猕猴A 77个通道的数据(M1 31通道,S1 21通道,PPC 25通道),使用猕猴B 78个通道的数据(M1 31通道,S1 31通道,PPC 16通道)[8].
1.2 实验范式
猕猴的实验范式按照图1所示流程进行.

图1 实验范式流程Fig.1 Process of experimental paradigm
如图2,猕猴按照提示灯1和提示灯2的指示进行实验,实验范式分为运动准备阶段(wait)、反应阶段(reaction)、伸手阶段(reach)和抓握阶段(grasp).各阶段之间由事件CenterHit、TargetOn、CenterRelease、TargetHit进行划分.主要流程为:
1)水平面板上,提示灯1点亮,提示猕猴可以将右手放置在触摸板上.当猕猴放置后,触摸板感受到猕猴手部压力,则为触摸成功,此时的事件命名为CenterHit事件,运动进入等待阶段;
2)当猕猴将手放在触摸板上维持500 ms后,水平面板上的提示灯1熄灭,位于垂直面板上的提示灯2点亮,提示猕猴可以开始抓握物体,事件命名为TargetOn事件,此时等待阶段结束,运动进入反应阶段;

图2 猕猴实验平台Fig.2 Rhesus monkey experiment platform
3)在猕猴接收到提示灯2点亮的提示后,手部离开触摸板需要一定的反应时间,当猕猴手部离开触摸板,伸向抓握物体时,触摸板感受不到压力,此时事件为CenterRelease事件,此时反应阶段结束,运动进入伸手阶段;
4)在猕猴手部触摸到目标物体时,此时事件为TargetHit事件,此时伸手阶段结束,运动进入抓握阶段;
5)猕猴手部触摸到目标物体,并保持抓握姿势200 ms,则认为抓握运动完成,此时抓握阶段结束,一次完整实验成功[8].
2 方法
2.1 锁相相位的计算
本文使用MATLAB对LFP信号进行了delta段(1~4 Hz)的滤波,并按照事件CenterHit和TargetHit+0.2 s的时间标签(timestamp),对全部的spike timestamp和LFP信号进行运动时间范围内的截取,即保留
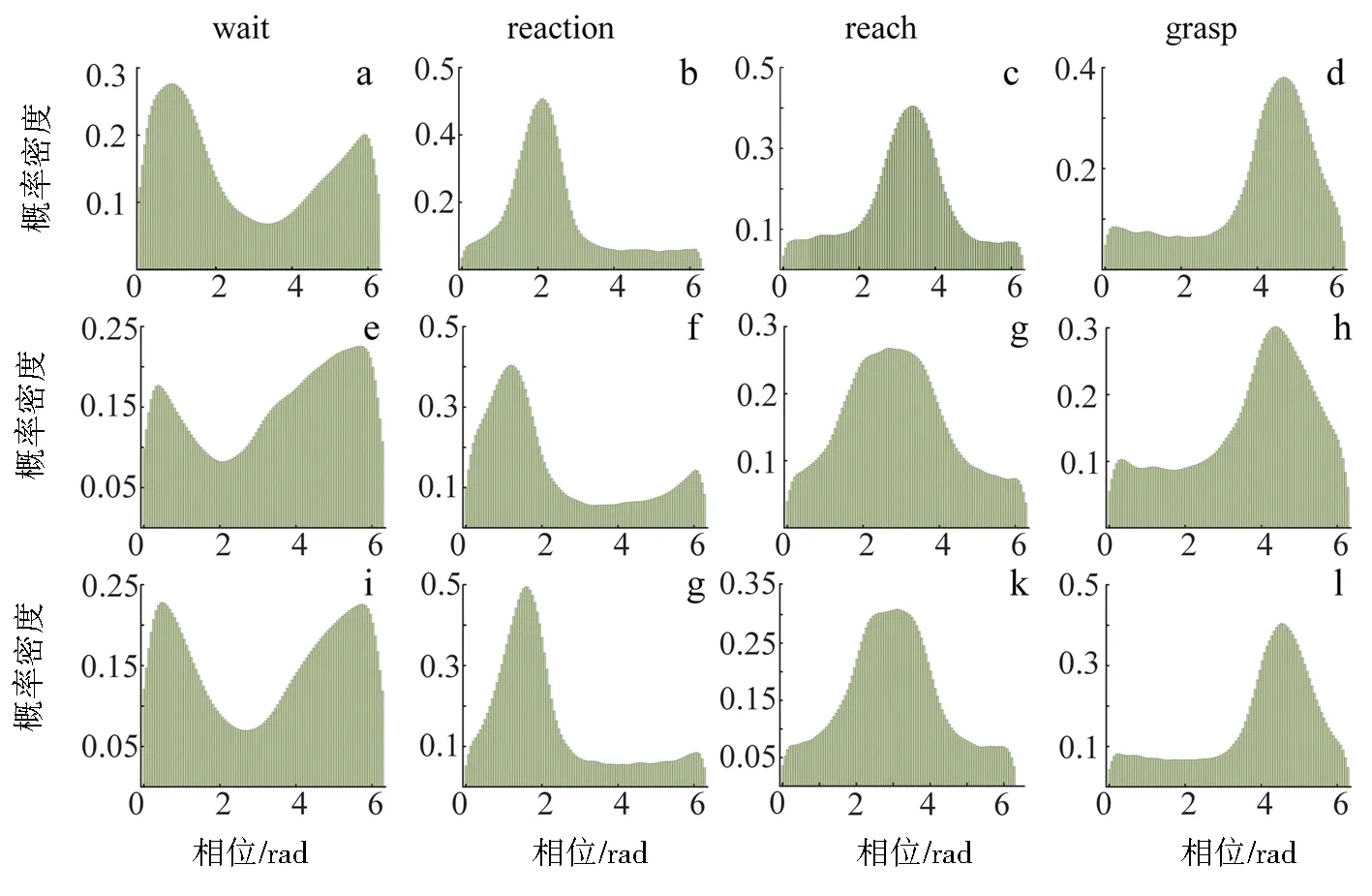
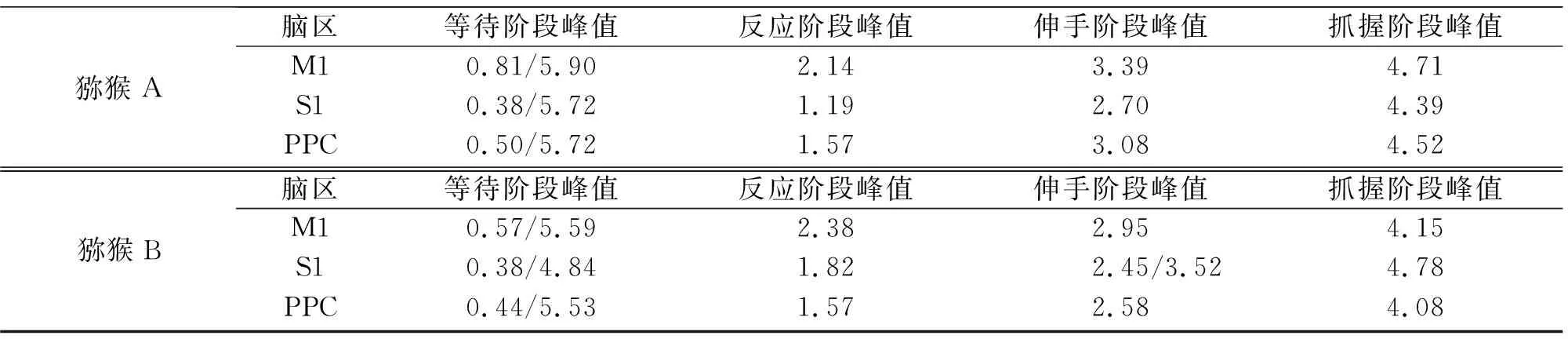
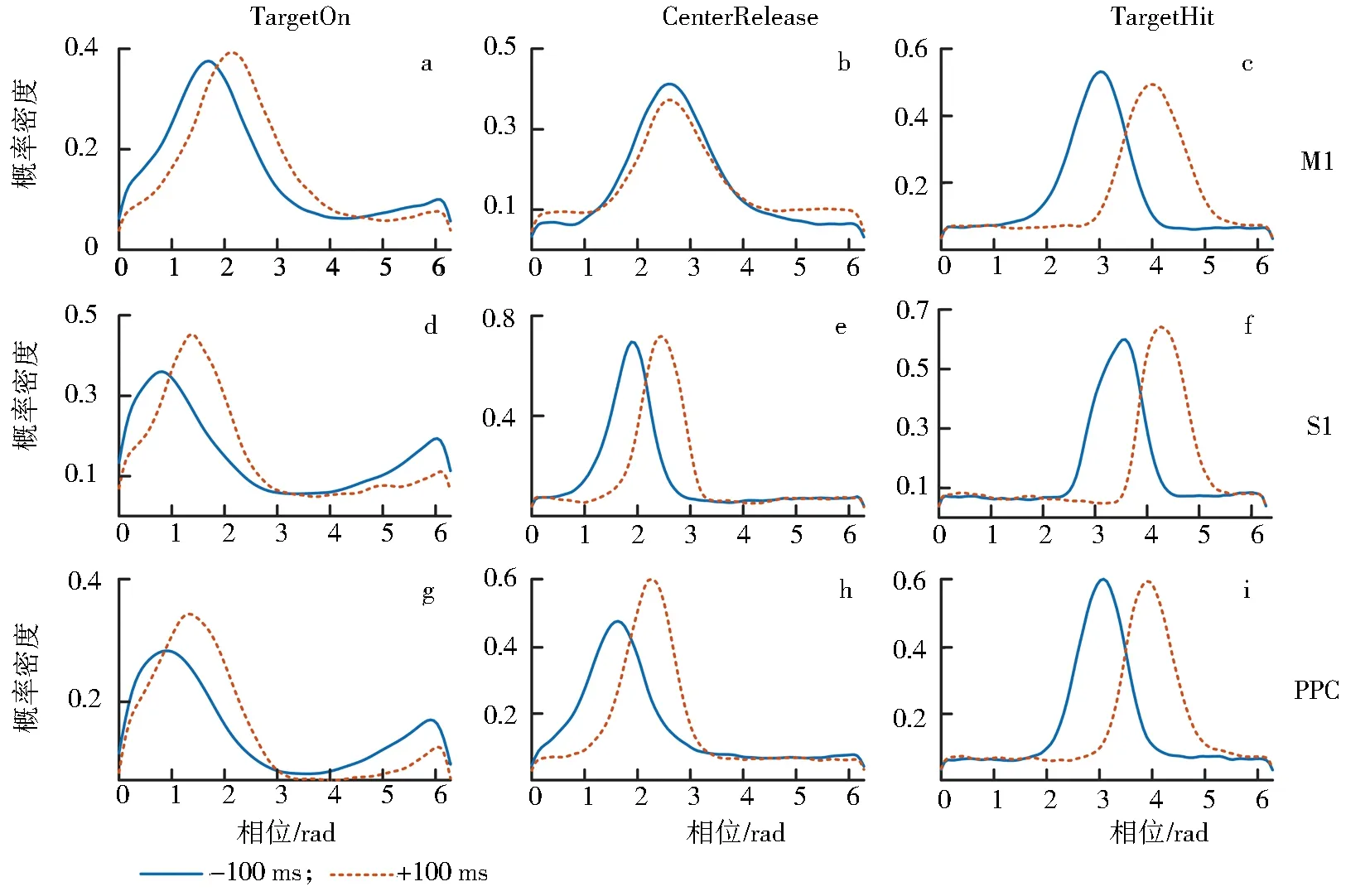
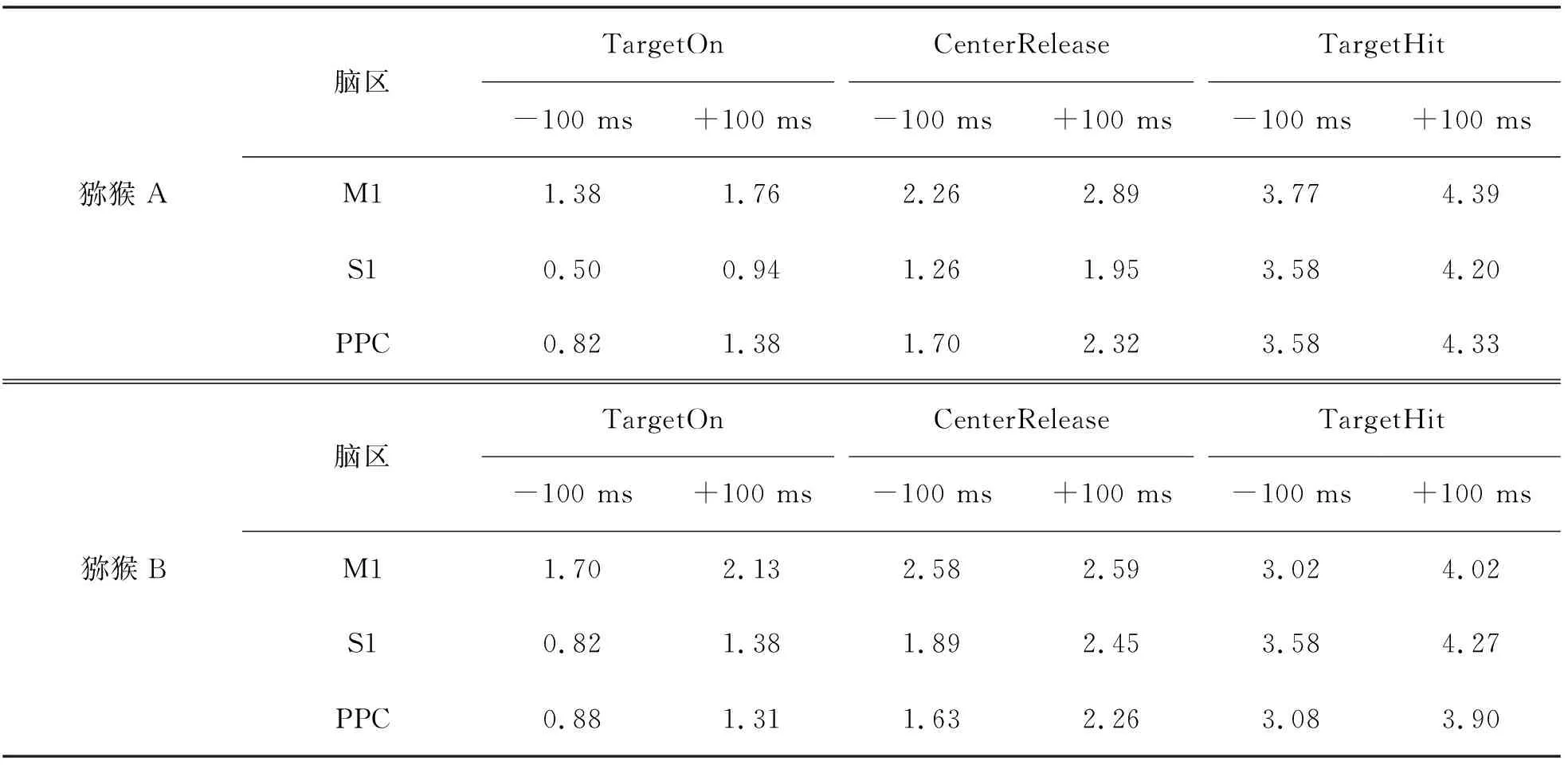
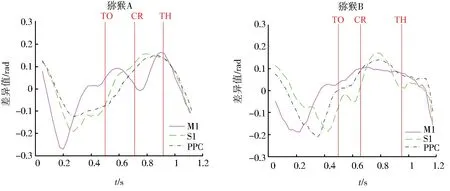
TCenterHit (1) 其中X表示spike timestamp或LFP的数据,TCenterHit和TTargetHit表示事件CenterHit和TargetHit发生时的timestamp. 完成后对LFP信号进行Hilbert变换[9]提取瞬时相位,具体计算过程如下:对于LFP信号y(t),y表示时间t点上的场电位值,其定义解析信号z(t)表示为 z(t)=y(t)+iHy(t), (2) 其中虚部Hy(t)是y(t)的希尔伯特变换,则信号的瞬时相位为 φ(t)=Atg(z(t)). (3) 为方便计算,本文使用CircStat工具箱将所有的角度转化为弧度[10],角度转化为弧度的计算公式为 (4) 其中αdeg表示相位角度值,αrad表示相位弧度值.对小于0的弧度值加上2π后调整为正数,保证所有的LFP相位弧度值在0~2π内,便于后续分析.接下来按照通道为所有spike timestamp找到对应的最近时间点的LFP delta节律的相位,若找到的时间点与spike timestamp的时刻相差超过0.01 s,则认为该spike timestamp无对应的锁相相位.将所有的spike timestamp对应的锁相相位按照脑区和通道分类进行保存用于后续的分析. 按照CenterHit、TargetOn、CenterRelease、TargetHit 4个事件的timestamp对锁相相位进行运动阶段的划分. TCenterHit (5) 其中,Xwait、Xreaction、Xreach和Xgrasp表示截取后等待、反应、伸手、抓握4个运动阶段的数据,TCenterHit、TTargetOn、TCenterRelease、TTargetHit表示CenterHit、TargetOn、CenterRelease、TargetHit 4个事件的timestamp. 每个脑区内所有通道的锁相相位叠加起来即代表该脑区的所有锁相相位,使用MATLAB软件函数ksdensity对各运动阶段的锁相相位进行概率密度分布计算以分析其分布特征,分析范围为0~2π,指定评估点为0~2π内的步长为0.02π的所有相位点;各运动阶段的相位通过Wilcoxon秩和检验进行两两阶段之间的统计学检验判断其是否具有显著差异性,当P<0.05时,认为其具有显著性差异[11]. 按照TargetOn、CenterRelease、TargetHit 3个事件的timestamp±100 ms内截取3个脑区的锁相相位,并对比分析2个窗口内的锁相相位概率密度分布的特点和峰值位置变化.对2个窗口内的锁相相位,基于其数据量较小的特点进行置换检验分析,判断两者之间是否具有显著性差异,当P<0.05时,认为具有显著性差异[12]. 为了进一步分析锁相相位随时间的变化情况,使用窗口长度(binlength)为100 ms,步长为25 ms的连续时间窗对猕猴连续运动过程中的锁相相位变化进行分析,窗口的起点(binstart)与CenterHit对齐,为保证数据整齐,窗口终点(binend)应该为binstart加上平均实验时长(triallength),即平均实验时长为所有单次范式完成时长的平均值,则每个窗口内的数据为 bini (6) 其中,i表示窗口的序数,xi表示当前窗口内的数据,bini表示当前窗口的起始点,当i为1时,bini=binstart,同时bini的值也代表当前窗口的时间点,当bini 对每个时间窗口内的锁相相位取均值作为该时刻锁相相位,即Xi=mean(xi),Xi表示当前窗口对应时刻的相位平均值.将所有通道的时间窗结果叠加作为所在脑区的时间窗分析结果,对每个窗口内的锁相相位进行概率密度分布分析,分析其锁相相位分布和峰值移动随时间的变化情况.同时将相邻2个时间窗内的相位均值相减,分析其均值差异随时间的变化情况. 如图3、图4所示,在运动的各个阶段,锁相相位呈现出了差异性的变化.猕猴A中,在M1脑区等待阶段,锁相的相位分布出现了双峰值的特点,双峰位置分别出现在相位0.81和5.90处;运动进入反应阶段后,峰值位置向后移动,位于相位2.14处;在伸手阶段,峰值在相位3.39处出现;在抓握阶段,峰值相位出现在4.71处. a、b、c、d.M1脑区;e、f、g、h.S1脑区;i、j、k、l.PRC脑区.图3 猕猴A在不同运动阶段的相位概率密度分布Fig.3 Phase probability distribution of monkey A at different stages a、b、c、d.M1脑区;e、f、g、h.S1脑区;i、j、k、l.PRC脑区.图4 猕猴B在不同运动阶段的相位概率密度分布Fig.4 Phase probability density distribution of monkey B at different stages 在同一脑区,猕猴B中,4个阶段呈现出相同的变化情况,但峰值位置有所不同,在等待阶段,猕猴B的锁相相位分布同样具有2个峰值,分别位于相位0.57和相位5.59处;在反应阶段,相位分布峰值向后移动,出现在了相位2.38处;在伸手阶段,相位峰值在2.95附近;进入抓握阶段后,相位峰值则位于4.15附近.峰值分布情况见表1.通过实验发现,在连续运动的过程中,相位分布峰值的变化随着运动的进行而不断向大弧度值移动,在等待阶段,3个脑区内都出现了双峰值的情况,在猕猴B的S1脑区进入伸手阶段,虽然也出现了双峰值的情况,但是其2个峰值的位置分别为2.45和3.52,峰值较为接近,与等待阶段不同. 表1 猕猴不同运动阶段锁相相位分布峰值 锁相相位峰值的变化,也体现在了各阶段相位均值的变化上,由图5可以看出,由于锁相相位在不同运动阶段的分布变化,使得相位的均值呈现出了一定的变化规律,在2只猕猴上的3个脑区中都呈现出了一致的变化特点,从准备阶段进入反应阶段后,相位均值出现降低,随后随着运动的进行,到伸手阶段时相位均值增加,到抓握阶段时到达最大值.两两阶段之间均进行过Wilcoxon秩和检验,检验结果P值均远远小于0.05,可以认为各阶段之间具有明显差异性. 图5 不同阶段锁相相位均值变化Fig.5 Variation of mean phase of phase-locking at different stages 一个脑区锁相相位的变化是该脑区所有通道锁相相位变化的综合体现,为了进一步分析脑区内锁相相位分布变化是否具有一致性,对每一个脑区内的各个通道的相位均值进行了计算,并统计其均值变化与脑区整体变化一致的比例,如表2所示,可以看出所有脑区内的通道变化相同的比例均大于60%,在猕猴B的S1和PPC脑区,这一比例达到100%. 表2 均值变化与脑区整体变化相同的通道比例 不同运动阶段由不同的事件进行划分,在事件发生时,对锁相相位变化的影响尚未知晓.为进一步分析运动过程中的锁相相位变化,对各事件发生前后100 ms范围内的锁相相位分布进行了分析,如图6、图7所示,TargetOn、CenterRelease、TargetHit 3个事件前后各100 ms内分别对应等待阶段和反应阶段,反应阶段和伸手阶段,伸手阶段和抓握阶段.结果显示,除猕猴B在CenterRelease事件前后,峰值无明显变化,其他脑区在各个事件前后各100 ms内,相位的分布依然发生着变化,且随着运动的进行,锁相相位的峰值在向后移动,峰值情况见表3.所有事件前后的锁相相位均经过置换检验,P值均远小于0.05,可以认为在事件发生前后的100 ms里,锁相相位分布发生了明显变化. 图6 事件发生前后100 ms内的猕猴A锁相相位分布Fig.6 Plase-locking distribution of monkey A within 100 ms before and after the events 图7 事件发生前后100 ms内的猕猴B锁相相位分布Fig.7 Phase-locking distribution of monkay B within 100 ms before and after the events 表3 事件发生前后100 ms内锁相相位分布峰值 在事件发生前后100 ms内的锁相相位中,其均值同样具有一些规律性的变化.如图8所示,在2只猕猴的M1脑区,各个事件发生后的100 ms内的锁相相位均值都要比事件发生前的100 ms内的锁相相位均值要大;但在S1和PPC脑区内,TargetOn事件发生的前100 ms内的锁相相位均值要比事件发生后的100 ms内的均值要大,即在等待阶段将要结束的最后100 ms内的锁相相位均值要比反应阶段开始100 ms内的锁相相位均值略高. a、b、c.分别为猕猴A的M1、S1、PPC;d、e、f.分别为猕猴B的M1、S1、PPC.图8 事件发生前后100 ms内的锁相相位均值Fig.8 Mean value of the phase-locking phase in bins of 100 ms before and after the events 在事件发生前后100 ms内,锁相相位发生了明显变化,这种变化是否是随着时间不断进行仍然未知,基于此,本文在连续时间窗口中分析锁相相位分布的变化情况,结果如图9所示.图9中TO、CR、TH分别是事件TargetOn、CenterRelease、TargetHit发生的时间.通过图9可以发现,锁相的相位分布变化是时刻都在发生的,但是在TargetOn事件发生后,即猕猴运动进入反应阶段后,锁相的相位分布开始有了更为明显的峰值变化,在等待阶段,虽然也有锁相分布峰值的出现,但是其分布较为平缓,这与在不同运动阶段讨论锁相相位分布的结果是一致的. 图9 连续时间窗下锁相相位概率密度分布变化Fig.9 Variation of phase-locking probability density distribution under continuous time bins 这种锁相分布峰值的陡峭性,由图9可知在CenterRelease发生后开始逐渐明显,即在由反应阶段到伸手阶段时,锁相的分布情况峰值更为明显,在进入伸手阶段后,锁相相位分布峰值愈加明显且峰值位置随时间逐渐变化. 本文对每2个相邻时间窗内的锁相相位进行了均值相减,其随时间变化的特征反应了锁相相位随时间变化的剧烈程度,如图9所示.从图10中可以看出在CenterRelease后突然增大的差异值,这代表了进入伸手阶段后,锁相相位变化速度的加剧.如表4所示,展示了2只猕猴各脑区出现最大差异值的时刻,该时刻表示了在本文所描述的猕猴伸展抓握实验范式中,spike与LFP的锁相相位变化最大的时刻. 图10 连续相邻时间窗的均值差变化Fig.10 Variation of mean difference between successive adjacent time bins 表4 连续相邻时间窗的均值差最大值时间 本文利用猕猴伸展抓握运动的实验信号,在M1、S1、PPC脑区,对连续运动中的spike发放时刻和LFP delta节律的锁相相位分布变化进行了研究.分别在运动的不同阶段,关键事件发生前后100 ms内和连续时间窗3种时间尺度下,对锁相相位的分布变化进行了分析. 猕猴在连续运动中的不同阶段,spike与LFP delta节律的锁相相位分布会发生显著变化,在不同脑区的不同阶段表现出了不同的相位分布特点和分布峰值位置. 为了进一步分析这种变化,对关键的事件TargetOn、CenterRelease、TargetHit发生前后各100 ms的时间窗内的锁相相位分布进行了分析,可以发现事件前后2个相邻100 ms内的锁相相位分布是具有显著差异性的,而且可以明显观测到锁相相位的峰值随时间推移逐渐增大. 为了细化分析这种峰值变化和时间的关系,本文使用连续时间窗对运动中各个时间点的锁相相位分布进行了分析,实验结果表明锁相的相位分布随时间不停变化,这种变化在CenterRelease前后最为明显,相邻窗口均值差异分析体现了相邻时间窗之间的锁相相位变化剧烈程度,可以看出在进入伸手阶段后,这种变化最为剧烈,通过计算,得出了变化最大的时间点. 综上所述,本文利用猕猴的伸展抓握运动范式,发现了峰电位与局部场电位delta节律锁相相位分布的变化规律,所发现的锁相相位的变化规律可以区分连续运动中的不同阶段,为研究大脑神经信息编码提供了一种新的思路. 致谢:本文实验中所使用的猕猴伸展抓握运动范式数据由军事医学研究院军事认知与脑科学研究所前沿交叉学科研究室提供,特别感谢该团队对本项工作的支持.2.2 不同运动阶段锁相相位分布
2.3 事件前后100 ms内锁相相位分布
2.4 连续时间窗对锁相相位概率密度分布的分析
3 结果与讨论
3.1 不同运动阶段之间的锁相相位分布差异


3.2 事件发生前后100 ms窗口内的锁相相位分布差异

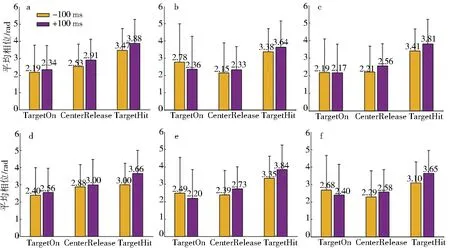
3.3 连续时间窗口下的锁相相位分布变化


4 结论

