鲁棒可信性优化的新进展

刘彦奎，刘颖

(河北大学 数学与信息科学学院，河北 保定 071002)

决策科学的一个重要特点就是决策环境中存在大量已知或未知的不确定性因素.现实中许多不确定应用问题都可以建模成一个优化系统，其中的约束条件既依赖于决策变量又与不确定参数的分布密切相关.例如在库存管理中，缺货约束就与订购策略和未知需求的分布有关.值得注意的是，缺货约束的处理方法严重依赖于未知参数的分布.根据可获知分布信息的类型和数量的不同，决策者采用不同优化手段对其分析处理.当不确定参数的分布只能获知支撑信息时，经典的鲁棒优化(robust optimization)[1]可以对这类问题进行有效的处理.此外一些研究者[2-3]尝试从大量的历史数据中估计不确定模型参数的概率分布，并采用随机优化(stochastic optimization)对不确定性进行建模.然而，现实中观察出不确定数据的随机性并进一步识别其准确概率分布非常困难，特别是对于大规模的实际应用问题[1,4].在一些实际应用中决策者根本无法获得大量历史样本数据，例如新书的发行量、新股的收益、新产品的需求等.在没有客观数据参考的情况下，通常采用相关领域的专家意见，以专家评判作为数据来源，因而专家数据也是普遍存在的重要数据来源之一.利用专家数据度量不确定现象可能性或可信性的相关理论和方法被称为模糊理论[5-7]和模糊优化方法[8].作为主观不确定性的有效研究方法[9]，其已被用于研究众多现实问题.这些研究都基于一个前提，即问题中不确定参数的准确分布都可以从专家经验中精确获得.

当不确定参数的可获知分布信息介于上述二者之间时，此时非精确分布在某些特定结构的分布集或分布族中变化，分布鲁棒优化方法(distributionally robust optimization)[10-11]是针对这类情况的一种有效建模范式.通常它采用一种基于“最差情形”导向的决策方法来处理各种应用问题并建立相应的优化模型.寻求这类模型的最优决策需要决策者在一个依据某种特征刻画的分布族中确定最差情况下的最优结果.对每一个分布信息非精确的鲁棒优化问题，非精确分布集的结构特征都是其求解的关键[12].现实情形中由于受到噪声、外溢值和偏见认识的影响，专家数据也存在不确定性，从而使得精确且完整的可信性分布信息也不易直接获得.决策者只能在模糊参数的分布信息部分知道的情况下制定相关的决策.注意到分布信息缺失通常会使决策者面临巨大的决策风险，导致严重的不良决策后果.因此，对现实决策问题中模糊参数不完整分布信息加以识别，并结合实际决策背景进行分析和建模就具有重要的研究意义.

模糊不确定决策系统中，模型参数的可信性分布信息部分可知时的优化理论和方法被称为鲁棒可信性优化理论或方法.针对此类模糊分布的不确定性，本文将从理论和应用2个方面对鲁棒可信性优化的相关研究进行综述，主要介绍鲁棒可信性优化的现有理论研究结果及实际问题的应用研究现状以便读者对该方法获得初步的认识.

1 鲁棒可信性优化理论

为了处理模糊分布中的不确定性，Liu等[13]提出了模糊可能性理论作为高维的模糊不确定性的新的公理化体系，在2-型模糊系统下建立了模糊可能性空间，其中的模糊可能性测度推广了普通的可能性测度更适合描述2-型模糊性.同时使用函数的观点给出了2-型模糊变量的定义，并提出了相关概念及计算方法.在常见2-型模糊变量中有1种特殊的类型：区间值模糊变量[14]，其第二可能性分布恒为1.因此在此类2-型模糊变量的三维结构中，只需分析其2型可能性分布即可.注意到其2型可能性分布是一个由可变分布构成的分布族，参数可能性分布在此分布族内围绕名义分布进行波动.依据可能性分布函数波动模式的不同，可以定义多种类型的区间值模糊变量并构建相应的非精确分布集.而非精确分布集的结构特征也决定了鲁棒可信性优化问题的处理和求解方法.

基于垂直波动方向，Liu等[14]给出了一类参数区间值模糊变量的概念，其2型可能性分布函数定义为[μξL(x,θl),μξU(x,θr)]，其中θl、θr分别是上下2个方面的波动参数，基于可变分布族的上下边界定义了上选择变量ξU和下选择变量ξL，并将二者的线性组合形式定义为参数选择变量ξλ，给出了一种单参数选择的分析方法.参数选择变量是从非精确分布族选出一个代表变量，它的优势特征是随着参数取值的不同，选择变量的分布可以遍历整个分布族，即分布族中每一个分布都与特定参数值下的选择变量与其相对应.即参数选择变量的分布可以代表非精确分布族中的所有分布.选择参数λ反映了决策者乐观或悲观的决策态度，单一参数的设定决定了决策者决策态度的一致性.此外，在可能性分布达不到1的广义情形下，Guo等[15]给出了广义参数可能性分布和广义区间值模糊变量的概念，该研究也属于单参数选择的范畴.随后Liu等[16]基于这2类单参数选择变量的共同点，给出了一个选择变量的新线性扰动形式并在此基础上构建了相应的非精确分布集.

决策者还可以采取其他多源化的选择方式，Chen等[17]给出了参数区间值模糊变量的交叉选择方法，该方法基于乐观和悲观决策角度给出了几种常用类型的交叉选择变量.具体地以正态变量为例，其悲观交叉选择呈现为在正态变量的左右半支上取最大分布和最小分布的组合方式.该方法的不足在于它是2种极端分布情况的结合，并不能灵活地刻画分布族中一般情形.随后Guo等[18-19]给出了双参数选择变量的概念，并采用双参数选择的观点对问题进行研究.这一方法中研究者设定了左右2个选择参数λ=(λ1,λ2)，不同参数值的选取呈现出决策者决策态度的变化性.同时随着参数值的变化该双选择变量也可遍历整个分布族，刻画出分布不确定性的变化范围.图1～图4以梯形模糊变量为例说明了单参数选择变量、交叉选择变量和双选择变量的区别，其中蓝色围出的区域是2-型梯形模糊变量的非精确分布族，红色标识出的变量是特定选择方法确定出的选择变量.

图1 2-型梯形模糊变量的非精确分布集Fig.1 Ambiguous distribution set of type-2 trapezoidal fuzzy variables

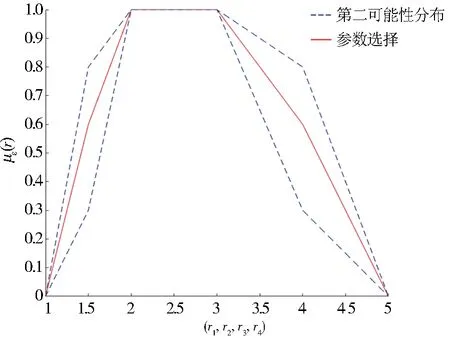
图2 单参数的选择变量Fig.2 Single parametric λ selection variable

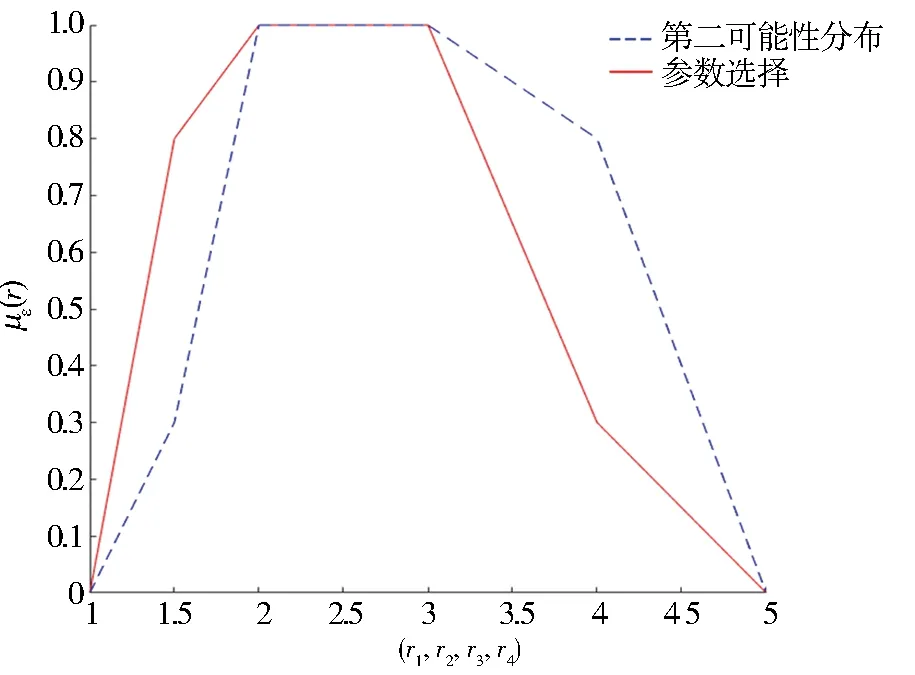
图3 悲观交叉选择变量Fig.3 Pessimistic cross selection variable

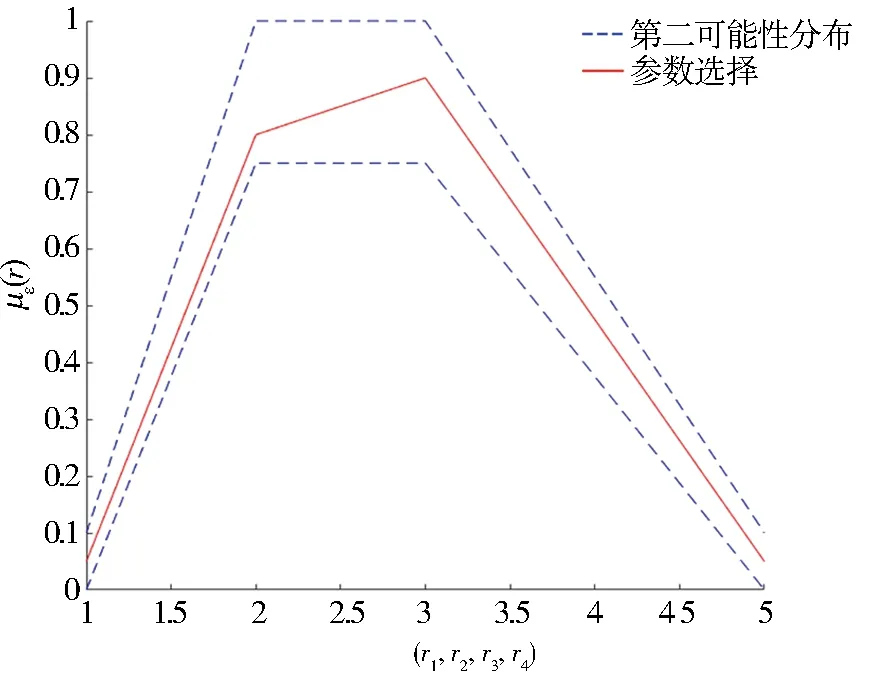
图4 双选择变量Fig.4 Bi-parameter selection variable

基于水平波动方向，Pei等[20]从水平集的角度提出了一种新的2型模糊变量：水平区间2型模糊变量，也是分布不确定性的有效建模工具.水平区间2型模糊变量借助水平波动参数，给出一种由名义可能性分布构造参数水平区间2型模糊变量的新方法.该方法提出的围绕名义分布的水平波动与前述讨论的垂直波动方式不同，给出的选择变量分布通过水平集来确定.值得注意的是该方法尽管是通过左右2个水平集定义选择变量，但使用了同一个选择参数属于单参数选择的范畴.

近来Liu等[21]在研究非精确可信性约束的鲁棒对等逼近问题时又给出了2类新的非精确分布集：基于指数函数的分布非精确集和基于支撑及期望信息的非精确分布集.在所提出的非精确分布集下，Liu等[21]找到了非精确可信性约束的安全逼近形式，得到的结果分别为计算上可处理的凸约束或线性约束形式.这些研究成果都推动了鲁棒可信性优化理论的前进和发展.

2 鲁棒可信性优化应用

鲁棒可信性优化方法是处理模糊可信性分布中包含不确定性的一类有效建模工具，已成功用于处理多种实际问题.该方法的广泛使用源于如下优势特征：1)该方法不需要不确定模型数据的完全分布信息.在现实中，由于应用问题的复杂性，通常很难估计和预测一些重要参数的分布.相反地不确定参数的分布信息只能部分获取，该方法可以对模糊参数的可信性分布不精确的情况进行有效建模.2)求解鲁棒可信性优化模型的难点在于其中的各类区间值模糊变量，这些变量中包含的高维不确定性使模型中的目标或约束通常难于处理.实际优化问题中针对特定变量类型，通过寻求目标或约束的鲁棒对等或安全逼近形式，可将鲁棒可信性优化模型转化为计算上可处理的等价模型形式.因此建模有效性和计算可处理性直接推动该方法多领域的广泛应用.

2.1 库存管理

在不确定的库存问题中，最优决策严重依赖于不确定市场需求.Guo等[19]在供应商收益最大的决策视角下研究了单周期库存问题，其中不确定市场需求的分布信息是部分可知的，并表示为广义参数区间值模糊变量.在该问题中零售商订购的商品只有单一品类.考虑到客户需求的多样化问题，随后Guo等[22]对多产品单周期库存管理问题展开讨论，其中不确定的需求和碳排放以可变的可能性分布为特征，并用广义参数区间值模糊变量进行刻画，以二阶矩为风险度量，在均值-矩优化准则下建立了一种新的鲁棒可信性多产品单周期库存管理模型，并设计有效算法进行求解.

2.2 可持续发展

可持续发展需要在不确定情况下实施适当的经济、环境、能源和社会的政策.Bai等[23]提出了一个针对可持续发展问题的分布鲁棒优化模型，其中不确定的人均国内生产总值、人均用电量和人均温室气体排放通过参数区间值可能性分布及其相关的不确定性分布集进行刻画；同时在强调决策环境的2个假设下建立了原始分布鲁棒可信性可持续发展模型的鲁棒对应，最后应用于分析阿拉伯联合酋长国的关键经济部门，为规划未来的劳动力和资源分配提供了定量依据.

2.3 投资管理

在金融投资方面，Liu等[14]提出了一个最小化投资风险的有价证券选择模型，其中收益风险通过总收益的二阶矩来度量，而不确定收益通过垂直波动的单参数区间值模糊变量进行刻画.Liu等[21]基于新的矩信息非精确分布集构建了一个鲁棒可信性风险值优化模型，同时导出其鲁棒对等模型并进行有效求解.在项目投资优化方面，鉴于有效的项目选择和员工分配策略直接影响组织或机构的盈利能力.Liu等[24]基于关键值优化准则，讨论了不确定性和交互作用对项目投资回报和员工分配的影响，其中不确定收益和员工能力用可变的参数可能性分布来表征.根据其结构特征，最终将原始鲁棒可信性项目组合模型转化为等价的非线性混合整数规划形式.

2.4 供应链管理

供应链网络设计是供应链管理中的一类重要问题，可以被看作设备选址问题的一个扩展.由于市场条件和需求的变化，制定采购和分销计划存在大量不确定性.Bai等[25]建立了一个可信性风险值优化模型，其中不确定的需求和运输成本以可变的可能性分布为特征，处理该问题时利用可能性临界值降低需求和成本不确定性的维度，最终得到了模型的等价形式.闭环供应链网络设计是更为复杂的网络设计问题，Liu等[16]基于一类新的非精确分布集考虑了不确定需求、运输成本和碳排放的不确定性，构建了闭环供应链网络的均值-上偏距分布鲁棒可信性优化模型.该模型权衡了经济成本的均值和上偏风险，为研究这一问题提供新的均值-风险架构.

协调供应链成员之间的行动和决策是推动供应链绩效改善的关键驱动因素之一.Guo等[18]解决了单周期3层供应链的协调问题，其中不确定需求以广义参数区间值可能性分布为特征.在风险中立的准则下，证明了集中决策中的供应链平均利润大于分散决策中的供应链平均利润总额.此外还研究了1个具有退货合同和退货政策的3级供应链并导出了不同成员最优订单量的解析表达式.Pei等[20]研究了双渠道供应链这一集中系统，其中制造商和零售商努力整合线上线下渠道，进而提高整个供应链的性能.该研究中制造商为使供应链的预期利润最大化寻求2个最优的定价决策：零售价格和直销价格，同时问题中的不确定需求通过水平区间模糊变量进行刻画.

表1对本文涉及到的相关文献在选择参数类型、不确定性位置和风险类型3个方面进行了区分便于分析识别这些应用研究.

表1 鲁棒可信性优化应用研究的分类

3 结论

对鲁棒可信性优化理论和应用方面的最新进展进行了综述.系统地总结和区分了不同波动方式下选择变量的定义方法.选择变量的概念将非精确分布集的分布不确定性导致的计算复杂度降低，同时保留原非精确分布集中不确定分布的重要信息.多种类型选择变量的参数可能性分布为实际优化问题提供了更灵活的决策，有助于促进鲁棒可信性优化方法的发展.大量相关研究的发表从理论和实际应用方面都证明了这一研究领域的活力，展示了鲁棒可信性优化方法的优势，为研究人员和从业者提供了更丰富的技术视角.此外预计诸如与非精确分布集相关的风险理论、鲁棒可信性大规模动态规划的可处理性等问题，特别是医疗、防疫等热点领域的应用特定框架将在未来几年受到广泛关注.