基于Vector Fitting的光伏并网逆变器控制器参数频域辨识方法

王 哲，吕 敬，吴林林，王 潇，宗皓翔，蔡 旭

（1. 上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2. 国网冀北电力有限公司电力科学研究院，北京 100045）

0 引言

近十年来，可再生能源发展迅猛，目前我国光伏和风电的装机容量均为世界第一。光伏并网逆变器是光伏发电单元与交流电网之间的关键接口装置，直接影响光伏发电系统并网的动态特性，因此对其进行精确建模至关重要。然而，实际中由于商业机密，厂家往往无法提供光伏并网逆变器的控制器参数，即存在“灰箱”问题。因此，需要根据实测数据对光伏并网逆变器的控制器参数进行辨识［1］。

目前，参数辨识方法主要分为2 种，即时域辨识法和频域辨识法。时域辨识法利用系统外部的时域测量数据来估计微分方程或状态方程的系数。文献［2］推导得出数字比例积分（PI）控制器的参数可唯一辨识，并通过时域测量数据辨识参数，验证了理论分析的正确性。文献［3］将光伏逆变器视作“黑箱”系统，仅通过采集逆变器外部的输入-输出数据，对光伏逆变器的数学模型进行辨识。文献［4］建立了典型电力电子电路的混杂系统模型，并基于该模型验证了可采用最小二乘算法来辨识电路参数。文献［5］提出一种在二次侧量测信号上施加扰动的虚拟量测激励方法，对光伏逆变器的直流电压外环和电流内环控制参数进行分步辨识。文献［6］采用自适应差分进化算法分2 步辨识内环和外环参数。文献［7］基于差分进化算法对电流内环控制参数及其限幅值进行了分阶段辨识。文献［8］忽略电流内环前馈解耦环节，利用粒子群优化算法分步辨识内环和外环模型参数。文献［9］通过注入指令功率扰动，采用粒子群优化算法辨识下垂控制并网逆变器的等效惯性常数与等效阻尼系数。文献［10］使用阻尼最小二乘算法，利用人为施加的扰动数据分步辨识dq轴电流环控制器参数。文献［11］研究了双馈风力发电机不同系统动态下观测量的选择对参数辨识精度的影响，并分步辨识了双馈发电机的机械和电气参数。文献［12］运用最小二乘回归方法研究了双馈风力发电机三相短路状态下的参数辨识方法。文献［13］提出了风电场集电网络简化等值模型的构建方法，并采用粒子群优化算法对该模型进行了参数辨识。综上，由于模型中多种时间尺度的环节相互混杂，某些频段的外特性与多个参数均存在耦合关系，为了简化混杂在其中的各种因素，实现待辨识模型结构的解耦或简化，获得更好的辨识效果，现有时域辨识方法大多采用分步辨识的方法，常需要针对性地选取扰动信号与观测信号来辨识不同环节参数。

频域辨识法通常用于估计频率响应、传递函数等，适用于具有不同带宽控制环节的电力电子变换器的参数辨识。文献［14］首先采用频域离散激励法测试虚拟同步发电机的功频外特性，然后通过复曲线拟合法辨识其功频控制回路的传递函数。文献［15］提出一种通过递推最小二乘法来拟合并网逆变器端口的dq导纳特性的方法。文献［16］推导了双馈风电机组转子侧的解耦模型，通过注入伪随机信号计算得到该模型的传递函数序列，并进一步辨识其内环和外环控制器参数。此外，上述文献对并网逆变器控制结构均做了一定简化，且未考虑锁相环。

本文提出一种基于Vector Fitting［17-19］的光伏并网逆变器控制器参数的频域辨识方法，该方法基于光伏并网逆变器的交流端口宽频导纳特性，能够准确获取不同带宽控制环节的导纳特征，实现多带宽控制环节参数的精确辨识。首先，建立光伏并网逆变器交流端口的dq导纳模型［20］，该模型包含光伏并网逆变器的全部控制环节，包括直流电压外环、电流内环、锁相环等。然后，通过扫频方法获得光伏并网逆变器交流端口的测量导纳数据，采用Vector Fit-ting 算法对测量的导纳数据进行矢量拟合，得到拟合导纳的标准传递函数表达式。最后，通过最小二乘原理使理论导纳标准式与拟合导纳标准式对应项系数的差值平方和最小，最终辨识得到光伏并网逆变器所有控制器参数的估计值。

1 光伏并网逆变器典型拓扑及控制

图1 为光伏并网逆变器典型拓扑及控制结构。光伏并网逆变器通常采用基于双闭环矢量控制的三相电压源逆变器结构，外环为直流电压控制，内环为交流电流控制，同时还需要锁相环提供电网角度用于同步旋转坐标变换。图中：Uabc和Iabc分别为电压源逆变器出口处的三相电压和电流；Uiabc为电压源逆变器经滤波器后的三相电压；Udc和U*dc分别为电压源逆变器的直流侧电压及其参考值；Idc为直流侧输出电流；Lf和Rf分别为电压源逆变器交流侧滤波电感及其等效电阻；θpll为锁相环输出的电网角度；Id、Iq和I*d、I*q分别为d、q轴电流及其参考值；Uid、Uiq分别为电压源逆变器经滤波器后的d、q轴电压；ω为系统基波角频率；Hc、Hdc分别为电流内环、直流电压外环的PI 控制器传递函数；Hpll为锁相环的PI 控制器传递函数。

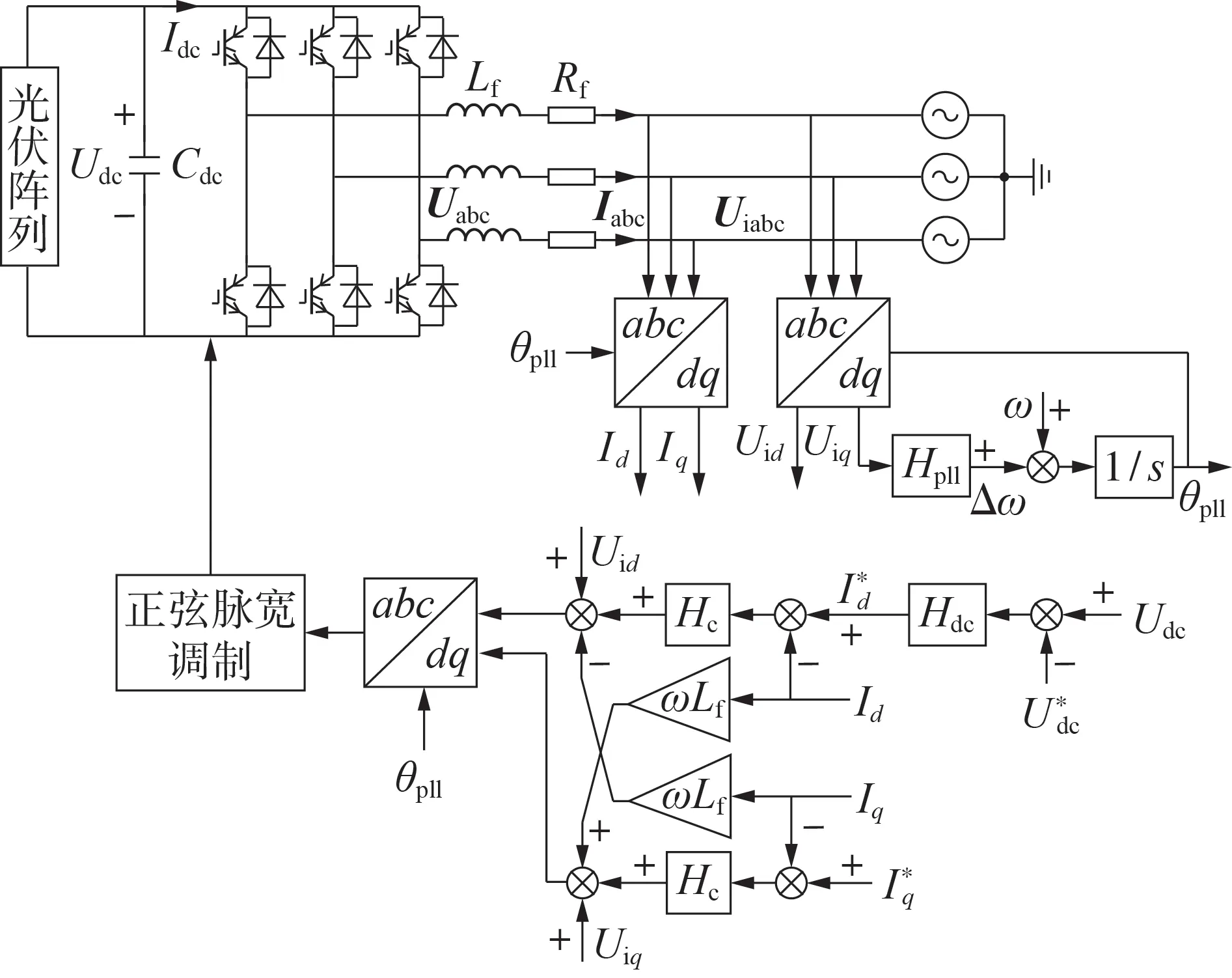
图1 光伏并网逆变器典型拓扑及控制结构Fig.1 Typical topology and control structure of photovoltaic grid-connected inverter

由图1 可得，光伏并网逆变器在dq坐标系下的交流侧数学模型为：

式中：Kpi和Kii分别为电流内环的比例系数和积分系数；Kpdc和Kidc分别为直流电压外环的比例系数和积分系数；Kppll和Kipll分别为锁相环的比例系数和积分系数。

同时，根据三相逆变器的交、直流侧功率守恒，有下式成立：

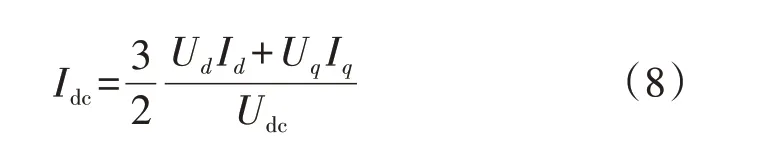
2 基于Vector Fitting 的光伏并网逆变器控制器参数辨识方法

2.1 Vector Fitting基本原理

2.1.1 算法原理

Vector Fitting 是一种迭代算法，每一次运算都以一组初始极点开始，通过求解线性最小二乘问题来重新定位初始极点至更好的位置，直至达到收敛。

在Vector Fitting 算法中，假设系统传递函数f̂(s)可以表示为如下形式：

由式（15）可知，初始极点在求解f̂(s)过程中被消去。因此，可以将σ(s)的零点作为新的初始极点，重新求解式（12），通过多次迭代得到更加准确的拟合结果。

2.1.2 初始极点的选取

关于初始极点，文献［17］提出选取初始极点时，要依照实数或共轭复数的形式，线性地或以对数间隔地分布在待辨识频率范围来选取。实极点常用于拟合光滑函数，一般情况下应选择共轭复极点。对于起始共轭复极点，实部通常选取为虚部的1/100，这有利于减少迭代次数。

另一方面，Vector Fitting 算法具有良好的鲁棒性，即使初始极点位置选取不佳，也能通过多次迭代得到准确的拟合结果。将σ(s)中的固定单位系数1变为未知参数，使σ(s)在高频处趋为1 的限制替换为一个更宽松的条件，极大提高了算法将极点重新定位至更好位置以及抗噪声干扰的能力，从而降低了初始极点选取的重要性。

2.2 参数辨识流程

本文要辨识的光伏并网逆变器的控制器参数为Kpi、Kii、Kpdc、Kidc、Kppll和Kipll。辨识流程图如附录A 图A1所示，具体辨识步骤如下。

步骤1：确定光伏并网逆变器的电气参数与控制结构。电气参数包括额定功率、额定直流电压、电网电压、直流母线电容值、交流侧滤波器参数等。

步骤2：理论推导光伏并网逆变器在dq坐标系下的导纳模型，将理论导纳模型中的第一行第一列元素Ydd(s)和第二行第二列元素Yqq(s)分别转化为标准的有理分式表达形式Gd(s)和Gq(s)，分别如式（17）和式（18）所示。之所以选取这2 个元素，是因为它们的阶次较低，便于算法拟合，且包含了全部待辨识控制器参数。Gd(s)和Gq(s)的系数特征为adn=1、aqn=1，其余各项系数均含有控制器待辨识参数，且均无虚部。

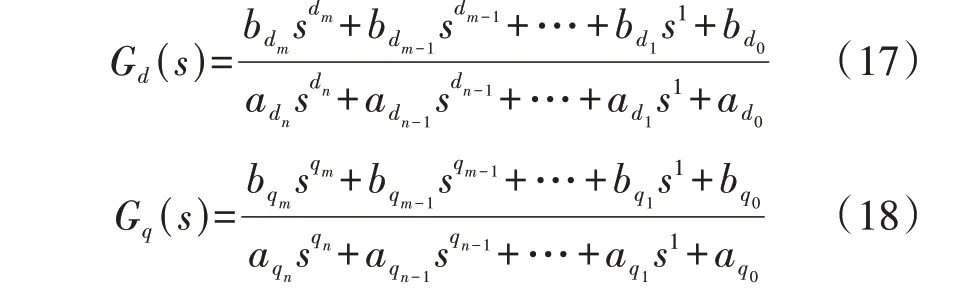
步骤4：采用Vector Fitting 算法求取Ydd扫频数据的拟合导纳Hd(s)。具体步骤为：将扫频所得Ydd及对应s（s=jω）作为算法输入参数，设置初始极点为算法默认值，得到拟合结果的有理分式表达形式如式（21）所示，其中a＇dn=1，a＇d0—a＇dn-1、b＇d0—b＇dm均为虚部远小于实部的复数，在接下来的最小二乘辨识过 程中，忽略a＇d0—a＇dn-1、b＇d0—b＇dm的虚部，只使用其实部。

进一步运用最小二乘算法来辨识控制器参数，具体做法如下。

首先，由于列向量M和N的元素间次数差距较大，需要合理分配它们的权重，从而使最小二乘原理更加适用。本文通过降低高次项次数，使M和N所有列向量元素次数保持在同一数量级，得到-M和-N，然后采用非线性最小二乘原理使列向量-M和-N的模最小来求解待辨识控制器参数。

其次，在最小二乘求解之前，需要将已知电路参数和电路运行稳态工作点信息代入，使得列向量M和N均只包含部分控制器参数，对于M和N独有的参数，在最小二乘求解后直接将其当作参数辨识结果，对于M和N共有的参数，需将二者的辨识结果取平均作为最后的辨识结果。

3 参数辨识实例

针对图1 所示典型双闭环控制的光伏并网逆变器，分别在光伏并网逆变器运行在50%有功功率输出、100%有功功率输出（无功功率输出均为0）这2种工况下，采用本文所提方法对其控制器参数进行辨识。需要注意的是，当电路有功功率输出情况改变时，电路的稳态工作点将会发生变化，控制器参数保持不变。

根据步骤1，已知系统电气参数和控制结构，电气参数如下：滤波电感Lf=1.4 mH，滤波电阻Rf=21.7 mΩ，直流电压Udc=780 V，直流侧电容Cdc=10 mF，电网电压为380 V，光伏阵列输出功率P=50 kW。

根据步骤2，推导计及所有控制环节的光伏并网逆变器的dq理论导纳模型，推导过程详见附录B。并将Ydd和Yqq元素转化为标准的有理分式表达形式Gd(s)和Gq(s)（如式（17）和式（18）所示），根据附录C 中该模型对应的Gd(s)和Gq(s)各项系数，得知Gd(s)中包含Kpi、Kii、Kpdc、Kidc这4个控制参数，Gq(s)中包含Kpi、Kii、Kppll、Kipll这4 个控制参数，根据式（17）和式（18）计算得到参数θi在频率f处的幅值灵敏度GM(θi，f)和相位灵敏度Gφ(θi，f)［20］如下：

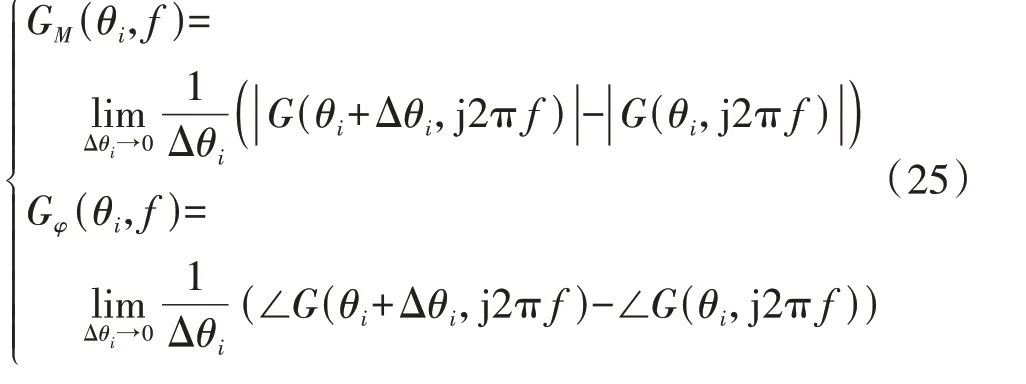
式中：| · |表示取模值；∠表示取相位；θi为第i个待辨识参数，Δθi为第i个待辨识参数的微小增量。

由传递函数Gd(s)和Gq(s)获得控制参数的灵敏度曲线如图2 所示。由图2 可以看出，Kpdc、Kidc、Kppll、Kipll幅值和相位灵敏度较大，相对容易辨识，电流环控制参数Kpi、Kii灵敏度较小，相对较难辨识，即电流环控制参数的辨识精度会相对差一些。另外，文献［21］指出，若所有参数的灵敏度曲线不同时过零点，则所有参数不相关，可以唯一辨识。由图2 看出，各参数的轨迹灵敏度曲线不同时过零点，故可以唯一辨识。

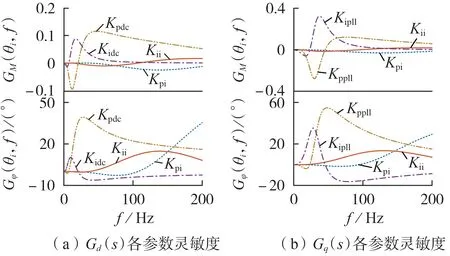
图2 Gd（s）和Gq（s）的各参数灵敏度Fig.2 Parameter sensitivities of Gd（s）and Gq（s）

根据步骤3，首先在交流端口处注入1～200 Hz的d轴小扰动电压，注入频率间隔为1 Hz，测量三相交流侧在dq坐标系下的d轴电流，采样频率为10 kHz，采样时间为1 s，通过FFT 分析，得到Ydd的扫频导纳曲线；同样地，在交流端口处注入q轴小扰动电压，测量q轴电流，得到Yqq的扫频导纳曲线。

2 种工况下Ydd与Yqq的扫频曲线与其理论导纳曲线的对比结果如附录D 图D1所示。可以看出，理论导纳与扫频测量导纳具有高度的一致性，验证了理论导纳模型的正确性。

根据步骤4，使用Vector Fitting 算法对Ydd和Yqq的扫频测量导纳数据进行传递函数拟合，对照推导得出的Gd(s)、Gq(s)的模型阶次，设定Vector Fitting算法初始拟合极点数为4，参数d、h均为0，附录E 给出了2 种工况下通过算法辨识得到的拟合传递函数的具体表达式。由于Vector Fitting 算法的结构特征，拟合结果Hd(s)、Hq(s)均是分子为三阶、分母为四阶的有理分式表达形式，且分子中s3的系数相对其他项系数非常小，可以忽略。

2种工况下拟合传递函数Hd(s)、Hq(s)曲线与测量导纳曲线的对比结果如附录F 图F1 所示，图中将误差幅值定义为同一频率下测量导纳与拟合导纳之差的幅值。由图可见，得到的拟合传递函数具有较高的精度，能够在较宽频率范围内精确拟合测量导纳曲线。

根据步骤5，令理论导纳标准式Gd(s)、Gq(s)和拟合导纳标准式Hd(s)、Hq(s)对应项系数差值的平方和最小（忽略Hd(s)和Hq(s)表达式分子中s3的系数），可得2 种工况下光伏并网逆变器的控制器参数辨识结果如表1 和表2 所示。通过误差百分比分析可知，本文所提控制器参数辨识方法能够在不同功率输出情况下较精确地辨识光伏并网逆变器的全部控制器参数；另一方面，电流内环PI 控制器参数Kpi和Kii的辨识误差相比电压环和锁相环较大，与前文的灵敏度分析结果一致。

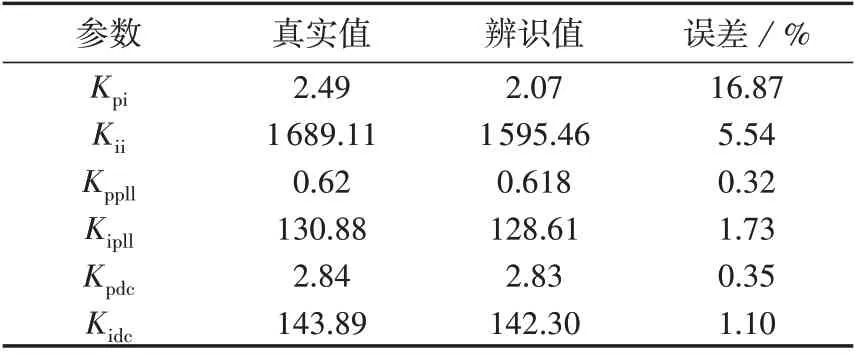
表1 50%功率输出时的参数辨识结果Table 1 Parameter identification results under 50% power output condition

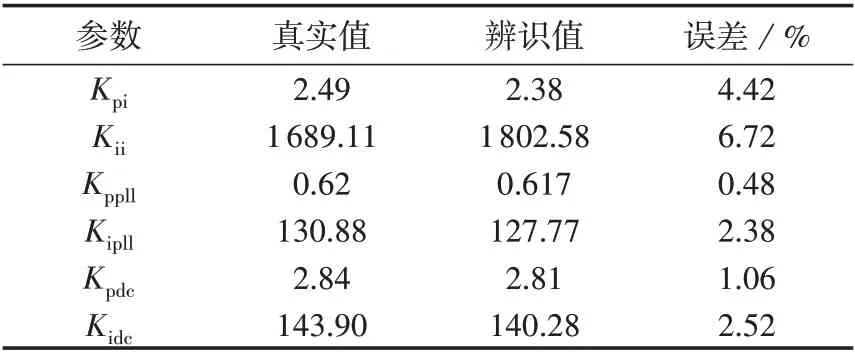
表2 100%功率输出时的参数辨识结果Table 2 Parameter identification results under 100% power output condition

在2 种工况下，将控制器参数的真实值和辨识值分别代入理论导纳矩阵模型中，并绘制其各元素的幅频曲线，如附录F 图F2 所示。由图可见，在不同功率输出情况下辨识得到的控制器参数均能够在宽频范围内保持原有端口导纳特性。

在实际应用中对逆变器端口进行小信号阻抗测量时，难免会存在噪声干扰。相比于传统的基于方程误差的复曲线拟合CCF（Complex-Curve Fitting）法［14］，本文所用的Vector Fitting 算法具备良好的抗噪声干扰能力。为了更好地说明这一问题，本文对100%有功功率输出工况下Ydd的扫频测量导纳数据加入线性信噪比为1 000 的噪声信号，采用2 种算法分别对加入噪声后的扫频信号进行传递函数拟合（拟合传递函数的具体表达式见附录G 式（G1）、（G2）），得到的拟合结果与误差曲线如附录G 图G1所示。由图可见，Vector Fitting 算法相对CCF 法，在待拟合扫频数据含有噪声的情况下，拟合得到的传递函数结果与扫频数据的误差更小，能够更准确地反映系统的端口频域特性。

利用2 种拟合方法得到的传递函数进行控制器参数辨识，辨识结果如表3 所示。可以看出，基于Vector Fitting 的参数辨识方法比基于CCF 的参数辨识方法具有更高的辨识精度。

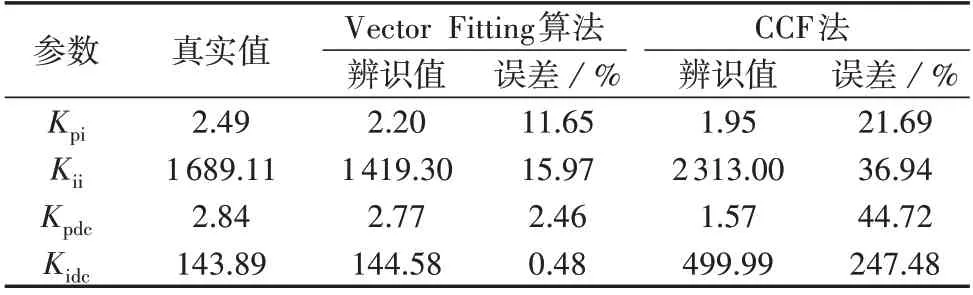
表3 噪声干扰时基于2种拟合方法的控制器参数辨识结果对比Table 3 Comparison of parameter identification results of controller based on two fitting methods under noise disturbance condition

4 讨论

针对本文所提参数辨识方法的适用性展开以下讨论。

1）本文通过小信号线性化建立光伏并网逆变器的端口阻抗时，认为电路工作在稳态，即正常运行工况下，控制环节中的限幅、保护等非线性环节并不影响电路的稳态工作点，也不影响电路的端口导纳外特性和参数辨识过程，因此对辨识效果的影响可以忽略。

2）在实际系统中，母线电容和交流滤波电感等参数的实际值与标称值可能存在一定的偏差，这会影响光伏并网逆变器的端口导纳特性，进一步影响控制器参数辨识结果的准确度。母线电容的参数偏差主要影响直流电压外环控制参数的辨识精度，交流滤波电感的参数偏差主要影响电流内环控制参数的辨识精度。一般情况下，母线电容和交流滤波电感参数偏差范围在±10%以内，分析表明，在该偏差范围内，母线电容和交流滤波电感的参数偏差对控制器参数辨识结果准确度的影响仍在可接受范围内。

5 结论

针对含多带宽控制环节的光伏并网逆变器，提出一种基于Vector Fitting 的控制器参数频域辨识方法，给出了具体的参数辨识步骤，并通过参数辨识实例验证了所提方法的有效性。得出以下结论：

1）采用Vector Fitting 算法对测量导纳数据进行矢量拟合，具有良好的抗噪声干扰能力，所得拟合传递函数表达式能够在宽频范围内精确表征测量的导纳曲线；

2）所提方法基于光伏并网逆变器的交流端口宽频导纳特性，能够准确反映不同带宽控制环节的导纳特征，从而实现不同带宽控制环节控制器参数的精确辨识；

3）所提控制器参数辨识方法特别适用于含不同带宽控制环节的电力电子系统的参数辨识，并可扩展应用至风电机组、柔性直流输电系统等不同场合。

附录见本刊网络版（http：//www.epae.cn）。